平面与空间上的余面积公式

郭洪欣，张楚楚，陈 璇

(温州大学数理与电子信息工程学院，浙江温州 325035)

在《数学分析》的教学实践中，结合温州大学本科生科研课题，本文的第一作者指导第二、第三作者，用本科生的基础知识推导了平面与空间中的余面积公式，这里用的内容是重积分的参数变换雅可比矩阵的计算、隐函数求导公式，同时结合第一型曲线积分、第一型曲面积分等，这些都是教学中的重点.无论从本科生科研课题，还是教学上来讲，本文都具有较好的借鉴意义.余面积公式适用于当区域是由函数的等值面刻画的时候.

我们知道，平面中半径为R的圆周周长是2πR，所围面积是πR2，前者是后者的导数.空间中半径为R的球面表面积是4πR2，所围球体的体积是4πR3/3，前者也是后者的导数.学生在学习过程中，很容易发现这个事实，也很想知道，它背后的数学原理是什么？这种规律并不能想当然地推广，例如边长为a的正方形，周长是4a，面积是a2，并没有导数关系.那么怎样去给出正确的公式？这就是我们要讨论的余面积公式及其推论.

作为牛顿-莱布尼兹公式的推广，二重积分的格林公式、三重积分的高斯公式给出了重积分与第二型曲线、曲面积分的关系.余面积公式给出的是有界区域的面积与其边界上的第一型曲线、曲面积分的恒等式.在黎曼几何中，余面积公式有更一般的表现形式和广泛的应用，读者可参阅文献[1-4]等.在本文中，我们需要的知识仅限于大学《数学分析》，可参阅文献[5-6]等.

1 二维余面积公式与例子

先讨论2维的情形.设f(x,y)是可微函数，我们假设其梯度∇f≠(0,0)，这样在D中每点的邻域，等值面f(x,y)=r总存在隐函数y=y(x,r)或x=x(y,r).

定理1 设D={(x,y):c1≤f(x,y)≤c2}，L(r)={(x,y)∈D:f(x,y)=r}，则区域D的面积可由下式计算：

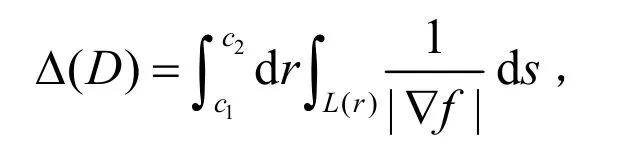
这里ds是弧微分，是第一型曲线积分.

证明：D的面积我们先假设在用参数(x,r)来计算.设在其雅可比行列式为：所以有：

根据重积分的参数变换，有：

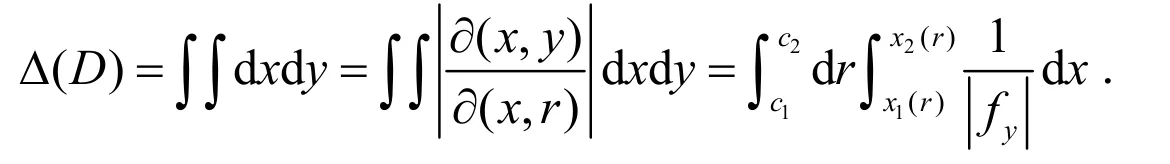
注意到L(r)的弧微分可得上式里面的积分：

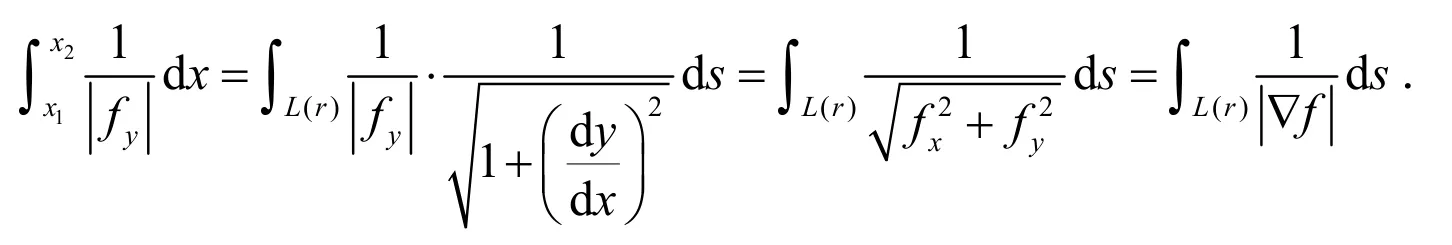
如果在D上fx≠0，可以用参数(y,r)计算，得到相同的公式.而对于更一般的情形，我们把使得fx=0的区域记为D1，D1在D中的补集记为D2，分别在D1与D2上用参数(x,r)与(y,r)计算，再利用积分的可加性即可.证毕.

直观地说，当区域由函数的等值面（二维的情形实际上是等值线）刻画时，L(r)与L(r+Δr)之间的面积，近似为等值线L(r)的长度乘以高得到，注意Δr是函数值f的变化，它所对应的定义域(x,y)的变化是从曲线L(r)到L(r+Δr)的距离，是我们需要的“高”，记为h，它是与点有关的.注意到梯度向量∇f为其等值线L(r)的法向量，所以L(r)与L(r+Δr)之间的面积近似为再对r积分就得到面积.

下面先举两个简单的例子来看余面积公式的应用.

例1 求由x≥0，y≥0以及{(x,y)|x+y=1}所围成的闭区域A的面积.

解：设f(x,y)=x+y，例1中区域可以表示成{(x,y)|x+y=r,0≤r≤1}.因为

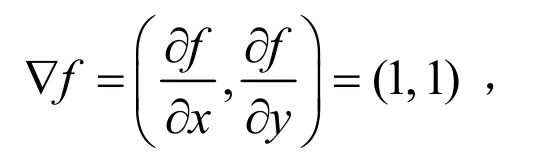
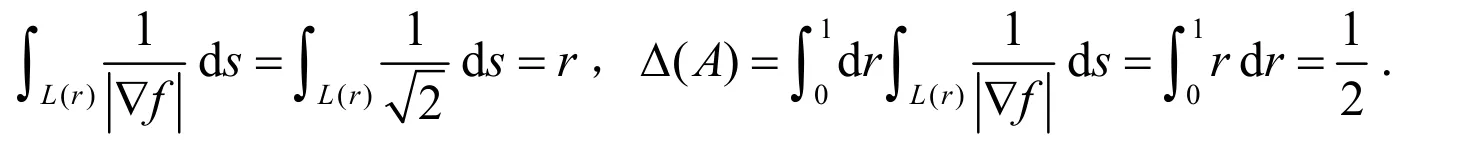
例2 求圆周{(x,y)|x2+y2≤R2}所围圆D的面积.

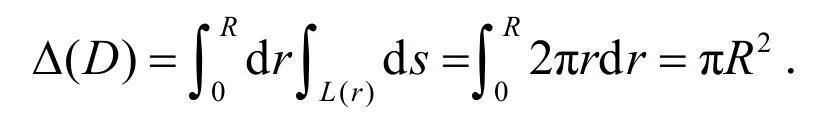
2 三维余面积公式

对于3维情形，我们有类似的：

定理2 若空间有界区域V可表示为V={(x,y,z):f(x,y,z)=r,c1≤r≤c2}，则V的体积这里A(r)={(x,y,z):f(x,y,z)=r}为f的等值面，dS为A(r)的面积微元.

证明：假设fz≠0，对于一般的情形，采用定理1相同的处理.做参数变换，令

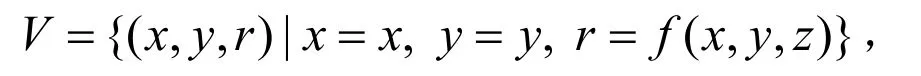
则由重积分的参数变换公式，需计算其雅可比矩阵：

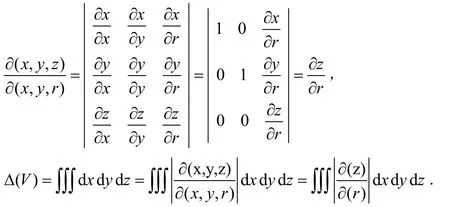
方程r=f(x,y,z)确定了隐函数z=z(x,y,r)，由隐函数求导公式，有：

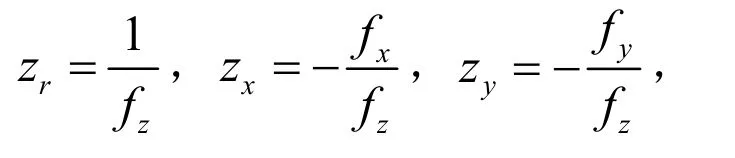
代入到体积公式，并注意到A(r)的面积元可得：

3 进一步的讨论

由定理1、定理2可以得到如下推论.

定理1、定理2与推论1告诉我们，一般情形下，图形的面积与其边界曲线、体积与其表面之间的关系。特别地，当f是距离函数时，其梯度是单位向量，就是我们在开始提到的圆面积与其周长、球体积与其表面积之间的关系.

从余面积公式的表达式看到，如果f不可微的点是有限个，也是成立的.例如，本文开始提到的正方形，其面积与其边界上的曲线积分的关系，如下给出：令则D={(x,y):0≤f(x,y)≤r}是边长为的正方形内部，Δ(D)=2r2，在推论1的1）中：这是Δ(D)=2r2的导数.