数形结合在高中数学解题中的应用

摘要：数学是研究“数”与“形”的学科，而数形结合思想作为数学学科的一种基本思想，对数学解题有着很大的积极作用。文章从数形结合解题的实例出发，体会数形结合对解题的简便作用。

关键词：数形结合;高中生;解题

数学是研究数量关系与空间形式的一门科学，“数”与“形”是数学学科的主要研究对象，“数”具有抽象与形式化的特点，而“形”具有具体而形象化的特点[1]，利用数学结合思想，把数与形之间相互转化，能够使抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，有助于高中学生把握数学问题的本质[2]。

一、数形结合的概念及解决问题的对象

数形结合，是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的一种思想，它主要有“以形助数”、“以数解形”两种形式。著名数学家华罗庚先生就曾以“数缺形时少直觉，形缺数时难入微”来描述这一思想的重要性。

初中数学中数轴这一知识点使学生首次体会数形结合，而在高中数学中，这一方法使用更加普遍：在集合中，韦恩图是数形结合的体现，它能够更清晰地表示各个集合之间并、交、补的关系;在函数中，定义域、值域、函数的性质都可以借助数形结合来分析;在方程与不等式中，方程的根与函数图像的零点有着对应关系，线性规划问题也是数形结合的体现;在立体几何中，借助数形结合学生可以更直观地分析点、线、面之间的关系，领悟相交、垂直、异面、线面平行、线面相交、二面角等知识点[3];在圆锥曲线中，圆、椭圆、抛物线、双曲线等是重点内容，在高考中占有较大比重，灵活运用数形结合思想，可将几何性质与代数研究牢牢结合，有助于学生厘清知识脉络。

二、数形结合的具体应用

在解题过程中，发现数形结合思想应用非常广泛，并且这一思想的应用，使解题更加简洁、直观。

1.运用数形结合，使问题由繁到简

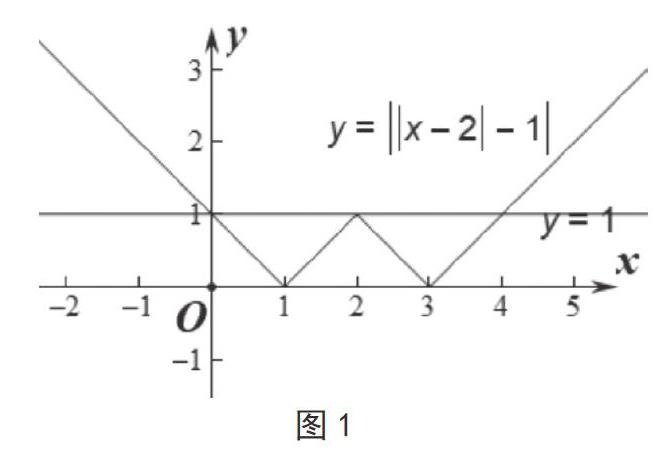
例1关于x的方程||x-2|-1|=a有三个整数解，求a的值。

分析：要想解这个方程，学生很容易想到去两次绝对值，①若

|x-2|-1=a，当x≥2时，x-2-1=a，当x<2时，2-x-1=a;②|x-2|-1=-a，

当x≥2时，x-2-1=a，当x<2时，2-x-1=a，分别对这两种情况进行解不等式，最后结合a的取值范围求出a=1，但这种方法情况较多，解起来较为繁琐，并且容易忽略a的取值范围和绝对值的非负性得到错误的结果。对于这个方程，用数形结合的思想，画出它的函数图像如图1，把方程解的个数问题转化为函数交点的问题，很容易可以判断只有当a=1时，此方程有三个整数解。

2.运用数形结合，使问题由繁琐到具体

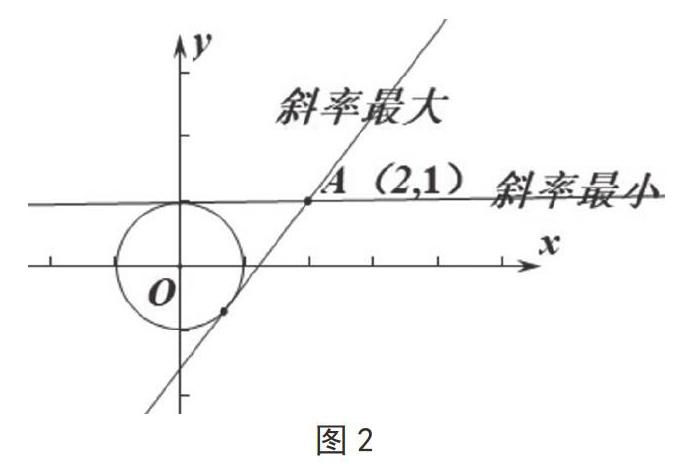
例2求y=的值域。

分析：由此题的形式想到两点之间的斜率，问题可以看成点A（2，1）和动点B（cosx，sinx）连线的斜率，又由于动点B的轨迹是单位圆，此题就转化成求过定点A与过点B的直线L：y=k（x-1）+2斜率的范圍，如图2，当直线与单位圆相切时取最值。本题利用数形结合，抛开繁琐的计算，使问题变得具体化。

三、应用数形结合解题的注意事项

1.等价转换

在运用数形结合时，数与形之间的转换是关键一步。对于式子较为繁琐、不易找出变量之间关系的题目，要转换思考角度，把它转化为直观的图形;而对于图形，为了分析它所表达出来的特性，要用数字表示关系，使解题思路更加具体。但是在转换过程中，要始终遵循等价原则，使转化前后的条件一致，如在三角函数中，运用数形结合要注意不能改变函数的定义域、值域。

2.精准作图

数形结合的运用始终与图形相关，能准确地画出所需图像是正确做出题目的基础。但若作图不规范，很可能导致解题错误，如常见的交点个数问题，会因图像的不规范性使最后结果与正确答案出现偏差，这就需要在作图的时候尽量精确，并且运用代数的精确性来验证。此外，对于图形的平移、伸缩变换也应牢固掌握。

3.灵活运用

数形结合只是数学思想中的一种思想方法，并不适用所有题目，所以，在解题过程中，要善于总结思考哪些类型的题目适合此种方法，而适合此种方法的习题应该如何应用，有效提高解题效率。

四、结语

数形结合思想作为高中学生必备的基本思想之一，远比数学知识重要得多，它为高中生解题提供有效思路，较为简洁与直观，不仅保留了数字的具体性，又有图形的直观性[4]，能够有效提高学生做题效率，增加学习兴趣，培养学生思维能力。所以教师与学生要充分重视、灵活使用这一思想，让它成为高中学生学习数学的金钥匙。

参考文献：

[1]李晶，孙雪梅，李德安.一题之探——以数形结合思想为例[J].数学通报，2019，58（04）：60-63.

[2]刘华.数形结合在高中数学中的应用[J].数学学习与研究，2019（09）：150+152.

[3]沈申文.数形结合思想在高中数学教学与解题中的有效运用[J].数学教学通讯，2019（09）：76-77.

[4]张登科.浅谈数形结合方法在高中数学教学中的应用[J].课程教育研究，2019（20）：118-119.

作者简介：张畅畅（1993-）女，汉族，河南大学数学与统计学院2018级硕士研究生，专业：学科教学（数学）。