高中数学多选题的命制实践与研究

安学保 王介花

【摘 要】 继上海、浙江之后，2017年山东省成为了第二批高考综合改革试点省市. 为了迎接新高考，笔者研究了高中数学多项选择题的命制方法，通过对多选题的命制实践以及学生答题数据分析，总结了多项选择题的命制和答题策略.

【关键词】 多项选择题;命制;答题策略

1 问题提出

高考恢复40多年来，不断尝试着新题型的探索实践. 数学多选型选择题（以下简称多选题）因为具有命题方式多样、考查容量大、能够涵盖多种数学核心素养、能够更好地区分学生不同的素养水平等特点，所以近年来受到命题者的追捧. 在新课程、新高考、新课标和新教材的背景下，多选题以其优越性可能会在数学评价中闪亮登场.

2 多选题的命制

笔者研究了数学单选题和多选型填空题，同时也研究了物理等其他学科多选题的命制方式，总结了四条数学多选题的命制方法.

从立意上看，多选题是数学核心素养的集中展示，可以是四基（基础知识、基本技能、基本思想、基本活动经验）的体现也可以是四能（发现问题、提出问题、分析问题、解决问题）的考查. 多选题可以直接考查学生的基础知识、基本技能的掌握情况，也可以考查基本思想和基本活动经验，测评学生分析问题和解决问题的能力，还可以设计新运算、新概念等新情境问题，测评学生发现问题和提出问题的能力.

多选题应该有合适的试题情境，有相应的题干和背景，而不是把单选题简单地变为多选题，更不是對现有的单选题直接进行否定而得到的.

多选题应该是同一情境下多个结论的判断，而不是把一些知识点凑在一起、把几个不相关的真命题和假命题放在一起类似于拼盘式的大杂烩.

多选题的每一个选项都经过精心设计，选项与选项之间具有知识的内在联系或者方法的相通性.

3 命制实践与分析

山东省2018级高中学生将会参加新课程标准指导下的新高考，为增强学生对多选题的认识，积累做题经验，同时了解和诊断济南市高中学生对数学多选题的认知基础，笔者在全市高一年级上学期学习质量评估考试试题中尝试进行了多选题的命制与考查.

整套试题共5页，23道题，全卷满分150分. 考试用时120分钟. 全卷试题类型包括：单项选择题、多项选择题、填空题和解答题. 多项选择题的指导语为“本大题共3小题，每小题4分，共12分. 在每小题给出的选项中，有多项符合题目要求. 全部选对的得4分，有选错的得0分，部分选对的得2分. ”多选题如下：

11.下面说法中错误的是（）.

A.经过定点P0（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示

B.经过定点P（x0，y0）的直线都可以用方程x-x0=m（y-y0）表示

C.经过定点A（0，b）的直线都可以用方程y=kx+b表示

D.不经过原点的直线都可以用方程xa+yb=1表示

E.经过任意不同的点P1（x1，y1）、P2（x2，y2）的直线都可以用方程（y-y1）（x2-x1）=（x-x1）（y2-y1）表示

命题意图 本题是一个综合判断型问题，意在考查逻辑推理素养，考查学生对直线方程的五种形式的理解，理解每种形式方程的使用限制条件.

答案是ABCD.

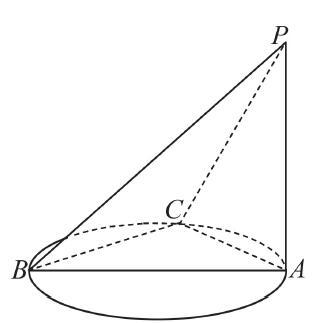
12.如图，PA垂直于以AB为直径的圆所在平面，点C是圆上异于A，B的任一点，则下面结论中正确的是（）.

A.PB⊥AC

B.PC⊥BC

C.AC⊥平面PBC

D.平面PAB⊥平面PBC

E.平面PAC⊥平面PBC

命题意图 本题是一个分析论证题，重点考查直观想象和逻辑推理素养，考查学生对线线垂直、线面垂直和面面垂直的推导证明和相互转化.

答案是BE.

13.定义“正对数”：ln+x=0，0 lnx，x≥1，若a>0，b>0，则下面结论中正确的是（）.

A.ln+（ab）=bln+a

B.ln+（ab）=ln+a+ln+b

C.ln+ab≥ln+a-ln+b

D.ln+（a+b）≥ln+a+ln+b

E.ln+（a+b）≤ln+a+ln+b+ln2

命题意图 本题给出了一个新概念，属于信息创新型问题，意在考查逻辑推理和数学抽象素养，考查学生对新概念的理解和运用.

答案是ACE.

本次考试在2019年1月22日举行. 最终参与统计的是济南市42所中学，实际考试人数是35835人. 学生采取答题卡答题的形式考试. 单选题和多选题是系统阅卷，其他题目由教师采取网上阅卷. 各学校任课教师为阅卷教师，与学生同时进行试题作答并完成相应的教师问卷. 下面根据得分情况逐题分析学生的做题情况.

通过表1可以看出，11题得4分的学生不多，但是得2分的学生比例能够占到0.824. 对比可以看出，选择一个正确选项、选择两个正确选项、选择三个正确选项得2分的学生人数依次构成递减数列，一半以上的学生是选择了一个正确选项得2分.

分析上述数据可以得出这个题目区分度很好，能够很好地区分出不同素养水平的学生. 得4分的学生共有1223人，素养水平最高，得2分的学生处于中等素养水平，得0分的学生不足两成，素养水平一般，数据呈现正态分布. 但是现行的赋分方式无法区分出选择一个正确选项和选择多个正确选项的学生的素养水平，显然这部分学生是具有明显差异的.

通过表2可以看出，12题得4分的学生比例是11题的四倍半，得2分的学生比例明显低于11题. 有6成的学生得0分. 上述数据分析说明学生对这个题目的认知度高，所以得4分的学生人数明显增多，这部分学生掌握的基础知识和素养水平都是非常突出的. 得2分的学生比例偏低，反而有6成的学生得0分，说明这个题的区分度不够，这种得分分布的原因还可能是答题策略的问题.

通过表3可以看出，13题得4分的学生少，得2分的学生中几乎都是选择一个正确的选项，得0分的学生超过一半. 上述分析说明这个题难度大，素养水平高的学生会这个题就能够得4分，素养水平居中的学生能选择出一个或者两个正确选项. 此题对素养水平一般的学生不具有区分度了.

4 答题策略

笔者通过问卷调查和访谈，了解和汇总了学生对于多选题的认识以及答题策略.

第一，学生对数学多选题抱有非常高的期望. 他们认为，多选题的得分率大于单选题，增加多选题的考查后能够提高自己的得分率，但实际测评结果恰好相反.

第二，部分學生表示，如果不确定选项的正确与否，那就当作单选题来做只选择一个选项，不会冒险选取多个选项争取4分. 但是学生同时也表示，对于会的问题还是会采取积极的得分策略，选择多个选项争取全部做对题目.

笔者访谈还发现了12题得分分布背后的秘密，那就是学生答题的心态和策略. 部分中等素养水平的学生认为会做这个题，所以在做这个题的时候并没有采取保守的选一个选项得2分的方法，而是选择多个选项努力争取得4分，但是结果出现了错选的情况，导致得0分. 这也反映出学生的知识薄弱点，对空间中的垂直关系掌握的不够扎实，感觉会做的题结果在考试中没得分.

5 小结

通过本次多选题的命题实践与研究，笔者认为多选题的素材选择以及选项的设计至关重要，另外多选题选项的个数设置为4个可能更好，这样能够适当减少试题的思维量和学生的答题时间;还有多选题的赋分标准有待于商榷. 多选题区分于单选题，应该鼓励学生选择多个选项，更好地发挥它的区分度，因此建议多选题的赋分标准设置为：“全部选对的得4分，有选错的得0分，选择一个正确选项的得1分，选择多个正确选项的得2分. ”

参考文献

[1] 任子朝，章建石，陈昂.高考数学新题型测试研究＼[J＼].数学教育学报，2015（2）：21-24.

[2] 任子朝，陈昂，黄熙彤，赵轩.新高考数学多选题考查功能研究＼[J＼].中国数学教育（上），2019（1-2）：3-5.

[3] 王文雅，李玉长.高考数学中“多选题”的类型分析＼[J＼].新课程学习（下），2015（5）：97-98.

[4] 何小亚.学生“数学素养”指标的理论分析＼[J＼].数学教育学报，2015（1）：13-20.

作者简介 安学保（1975—），男，中学高级教师. 济南市教育教学研究院评估部副主任.

王介花（1982—），女，中学高级教师，教育硕士.