感悟策略，激活思维，提升能力

摘 要：引导学生从多角度、多途径探索问题解决的策略，激活学生思维，提升学生的能力，是数学课堂教学的一项重要任务。文章作者对学生分数应用题常见的错误及原因进行分析，通过运用对比、正确使用画图、构建数学模型、引导学生归纳特性、转换思路等策略激活学生思维，提升学生的能力，阐述了自己的一些认识。

关键词：分数应用题;测试内容;解题方法

中图分类号：G623.5

文章编号：2095-624X（2019）24-0077-03

一、问卷设计与测试内容

受分数抽象性的影响，分数应用题一直都是学生的学习难点。为了更好地突破这一难点，我们对六年级119名学生进行了问卷调查和解题测试，希望调查及测试更好地了解学生的实际，寻求到解决问题的方法。

问卷调查结果统计如下表。

从表中可以看出，学生在解决分数和百分比应用问题时喜欢模仿例题解题。能够认真审题、找准单位“1”、做到量率对应、及时总结思路的学生并不多。可见学生在分析题意、画图助理解、思路总结等学习习惯方面存在一定问题。

为找出学生在解分数应用题中遇到的问题，笔者设计了一组单元知识测试题，共7题，测试时间：15分钟。

例一：一根绳子长20米，剪去4/5，还剩多少米？

例二：六（1）班学生向灾区捐书180本，比六（2）班多25%，六（2）班向灾区捐书多少本？

例三：六（1）班学生向灾区捐书180本，六（2）班比六（1）班多25%，六（2）班向灾区捐书多少本？

例四：有一袋大米，第一周吃了35%，第二周吃了15%，第一周比第二周多吃了45千克，这袋大米一共有多少千克？

例五：一本故事书240页，小玲第一天看了全书的 ，第二天看了全书的 。①小玲两天一共看了多少页？②第二天比第一天多看了多少页？

例六：修路队修一条长2400米的道路，第一周修了全长的15%，第二周修了余下的 ，还剩多少米没有修？

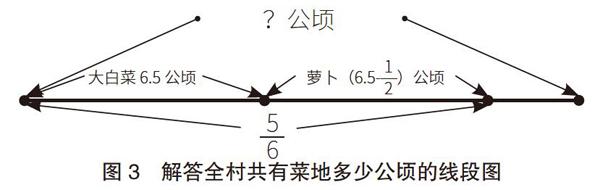
例七：李村种白菜6 公顷，种的萝卜比白菜少 公顷。这两种菜地共占全村菜地的 。全村共有菜地多少公顷？

二、具体错误及原因分析

测试后对个别学生进行访谈，确定每道错题的错误类型。根据对分数、百分数应用题错误类型的归因总结，可分为如下几种错误类型（见图1）。

1.分数意义理解不透彻

例一：一根绳子长20米，剪去 ，还剩多少米？

【错例】20- =19 （米）

【正确】20-20× =4（米）

【分析】把抽象的 误视为实际的量，可能是对分数意义不理解，也可能是粗心导致的。

2.误判单位“1”

例二：六（1）班学生向灾区捐书180本，比六（2）班多25%，六（2）班向灾区捐书多少本？

【错例】180×（1+25%）=225（本）

【正确】180÷（1+25%）=144（本）

【分析】典型的不一致问题，把六（1）班捐书数误为单位“1”，而实际却是六（2）班捐书数量为单位“1”的量。

3.数量与分率不对应

例三：六（1）班学生向灾区捐书180本，六（2）班比六（1）班多25%，六（2）班向灾区捐书多少本？

【错例】180×（1-25%）=135（本）

或180×25%=45（本）

【正确】180×（1+25%）=225（本）

【分析】没有认准已知数量的对应分率，误认为六（2）班占六（1）班的25%。

例四：有一袋大米，第一周吃了35%，第二周吃了15%，第一周比第二周多吃了45千克，这袋大米一共有多少千克？

【错例】解：设这袋大米一共有x千克。35%x+15%x=45或x-35%x-15%x=45。

【正確】解：设这袋大米一共有x千克。35%x-15%x=45。

【分析】分数应用题中，有时对应分率是隐藏的，部分学生在找隐藏的分率时没有注意对应，随意地在将已知的数量与分率建立关系。

4.受定式思维的影响

例五：一本故事书240页，小玲第一天看了全书的 ，第二天看了全书的 。

①小玲两天一共看了多少页？②第二天比第一天多看了多少页？

【错例】①240×（ + ）=76（页）

②240-76=164（页）或240× -240× =4（页）

【正确】①240×（ + ）=76（页）

②240× -240× =4（页）

【分析】由于问题①已经求了两天一共看的页数，学生受思维定式影响，解决问题②时，错误地运用了问题①的数据求出了还剩多少页没有看。也有的学生受“顺向思维”的影响，把较大数减去较小数。

5.没有准确把握单位“1”

例六：修路队修一条长2400米的道路，第一周修了全长的15%，第二周修了余下的 ，还剩多少米没有修？

【错例】2400×（15%+ ）=760（米）

2400-760=1640（米）

【正确】2400×15%=360（米）

2400×（1-15%）× =340（米）

2400-360-340=1700（米）

【分析】错因在于没有统一单位“1”。15%和 的单位“1”是不同的，因此这两个分数所表示的实际意义也不相同。第一周修的15%是针对整条路而言的，第二周修的 是针对剩下米数而言的，所以应该把“修了余下的 ”转化为整条公路的（1-15%）× 。

6.对数量关系理解不清

例七：李村种白菜6 公顷，种的萝卜比白菜少 公顷。这两种菜地共占全村菜地的 。全村共有菜地多少公顷？

【错例】（6 - ）÷ = （公顷）或

（6 + ）÷ = （公顷）

【正确】（6 - +6 ）÷

【分析】部分學生没有理解清楚数量关系：白菜的公顷数- 公顷=萝卜的公顷数，有的看成是“萝卜占全村菜地的 ”，有的看成“萝卜就是 公顷”，还有的看成“少白菜的 ”，反映出个别学生收集和加工信息的能力比较差。

7.其他因素

在实验或日常教学中，我们还发现，应用题的情节是学生熟悉的就容易解答，如果离学生生活较远的，学生就比较难理解。

例如：李村种白菜公顷6 ，种的萝卜比白菜少 公顷。这两种菜地共占全村菜地的 。全村共有菜地多少公顷？

对于土地耕种的问题，它与城市学生的实际生活相去甚远。测试结果表明，错误率较高，有34人做错，高达28.6%。有些学生在分析数量关系时特别困难，甚至无法清楚地解释两个相关量之间的关系。

三、解决对策

1.运用对比，助分数意义的理解，掌握解题方法

为了让学生了解分数当中带单位与不带单位的不同算法，从而更好地理解分数的意义，掌握解题方法。在课堂教学中，我们设计了下面的两道题进行对比。

（1）一根绳子长10米，剪去 米，还剩多少米？

（2）一根绳子长10米，剪去，还剩多少米？

教学中，教师应引导学生对两种题型中的不同含义进行理解，（1）题当中是剪去 米， 米是一个具体的量，直接用10- =9 （米）即可。（2）题可以将绳子总长看作单位“1”，将其平均分为5份，减去其中的4份，也就是剩下的是其中的一份，所以算法为：10×（1- ）或10-10× =2（米）

教师可以让学生在对比中分析题目的异同，加深学生对分数意义的理解，及时总结解题方法，有效激活学生的思维，进而提高学生的解题能力。

2.正确使用画图策略，化难为易，提升能力

数形结合的思想方法，是将抽象的数学语言与实际的直观图形结合起来进行思考。因为图形具有直接的表现力，它们可以达到简化复杂性的效果。因此，在教学中，我们可以引导学生通过画图生动形象地呈现分数的数量关系，变“看不见”的数量关系为“看得见”的数量关系，使学生的认知由模糊走向清晰，不断提高解决问题的能力。

针对“数量与分率不对应”这种错误，我们设计了对应的题目并结合线段图进行教学。例如：甲校图书馆有图书12000本，乙校比甲校的图书多25%，乙校有图书多少本？

用图2表示题意，能让题目的数量关系更加明确化，能让学生清晰找出乙校图书的对应分率，能有效地解决数量与分率不对应的问题，有助于学生理解和掌握分数应用题解题的关键及方法。学生的解题能力也能在画图过程中不断提高。

又如上述第七道例题：李村种白菜6 公顷，种的萝卜比白菜少 公顷。这两种菜地共占全村菜地的 。全村共有菜地多少公顷？

针对学生收集和加工信息的能力比较差、难以理解题目的特点，教学中，我们可以引导学生正确画出线段图（如图3），结合绘制的线段图理解应用题中复杂的数量关系，降低学习难度，提高学生解决问题的能力。

3.构建数学模型，激活思维，提升能力

数学课程标准在课程设计思路中还指出：“在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，使学生体验从实际背景中抽象出数学问题，构建数学模型、寻求结果、解决问题的过程。”因此，在数学教学中，数学教师应当注重和发展学生的模型思想，激活学生的思维，提高学生解决问题的能力[1]。

解决分数乘法问题是建立在分数意义的基础上。因此，其模型是：“一个数×几分之几=这个数的几分之几对应多少”。

例如：一根绳子长20米，剪去 ，剪去多少米？

在这个问题中，单位“1”是这根绳子的总长度20米，求剪去多少米就是求20米的 是多少。其模型是“绳子的总长度× =剪去的米数”。

正确运用这个模型，我们既可以帮助学生掌握分数乘法应用题的解题方法，又可以提高学生的解题能力。

又如上述第五道例题：一本故事书240页，小玲第一天看了全书的 ，第二天看了全书的 。①小玲两天一共看了多少页？②第二天比第一天多看多少页？①求小玲两天一共看了多少页就是求全书的 和全书的 共多少，其模型是“全书× +全书× =两天共看的页数”。同理求②第二天比第一天多看多少页，模型就是“全书× -全书× =第二天比第一天多看的页数”。

由此可见，分数乘法应用题的教学，需引导学生在分数意义这个已有的经验的基础上构建“一个数×几分之几=这个数的几分之几对应数”数学模型，需培养学生理解、运用模型的能力，从而促进学生能力的提升。

分数除法解决问题是建立在学生会用分数乘法解决问题的基础上的，因此我们同样可以利用乘法模型去解答分数除法问题。又如上述第四道例题：有一袋大米，第一周吃了35%，第二周吃了15%，第一周比第二周多吃了45千克，这袋大米一共有多少千克？

教学中，我们可以引导学生建立相应的数学模型：第一周吃大米的重量-第二周吃大米的重量=多吃的重量，即：大米的35%-大米的15%=多吃的45千克，有了这个模型，学生设未知数，列方程解答就行了。

对于稍复杂的分数乘除法应用题，我们同样可以引导学生在初步建立模型思想的基础上，举一反三、触类旁通。实践证明，经常让学生运用这种建模思想解决问题，学生就能在解题的过程中不断积累经验，掌握解题技巧及解题方法，学生的能力也会不断提升。

4.引导学生归纳特性，转换思路，提高能力

面对难度较大的分数应用题时，教师应当引导学生在对题目具有的普遍特征进行分析的基础上，将题目自身的特征找出来，依托不同的思路从不同的角度进行分析、解答。而在分数应用题的解答过程中，单位“1”能否准确确定是最为关键的内容点[2]。

如上述第六道例题：修路队修一条长2400米的公路，第一周修了全长的15%，第二周修了余下的 ，还剩多少米没有修？

对于此题，我们要引导学生分析题目的关键句（分率句），通过分析让学生明确：第一周修了全长的15%，是以公路的全长为单位“1”;第二周修了剩余长度的 ，单位“1”已变为剩余公路的长度，由于单位“1”都不同，因此必须进行转化，所以应该把“修了余下的 ”转化为整条公路的（1-15%）× 。让学生通过观察、分析，及时归纳题目特点，理清解题思路，促使他们掌握合理转化及分析思路，提升审题和发散思维能力，从而不断提升解题能力。

参考文献：

[1]李文福.建立数学模型，提高解决问题的能力——分数除法“解决问题”案例[J].小学教学参考，2014（11）.

[2]韦元爱.小学数学应用题有效教学策略之我见[J].科学中国人，2017（11）.

作者简介：谢淑雯（1976—），女，广东广州人，小学数学高级教师，本科。