基于深度信念网络的多品种水稻生物量无损检测
2019-12-06段凌凤潘井旭郭子龙刘海北覃建祥柯希鹏
段凌凤 潘井旭 郭子龙 刘海北 覃建祥 柯希鹏
(1.华中农业大学工学院, 武汉 430070; 2.华中农业大学作物遗传改良国家重点实验室, 武汉 430070)
0 引言
水稻是世界上最主要的粮食作物之一,高产一直是水稻育种与栽培的重要目标[1-2]。水稻生长发育中的生物量积累是经济产量(以下简称产量)的物质基础[3-4]。不同品种生物量积累动态规律[5-6]及各生育阶段生物量与产量的关系不一致[7],连续测量不同品种的水稻生物量,对研究不同品种生物量积累动态和水稻产量形成规律、指导水稻生产及育种具有现实意义。
近年来,已有学者在基于图像特征的作物生物量测量模型构建上进行了探索研究。梁淑敏等[7]以植株图像周长为表征因子,建立了玉米鲜生物量测量模型。更多研究则基于植株不同角度下投影面积构建生物量测量模型,如基于顶视投影面积[8]、基于2幅互呈90°的侧视投影面积[9]、基于顶视投影面积与2幅互呈90°侧视投影面积[10-13],以及基于多幅侧视投影面积平均值与顶视投影面积[14-15]等。研究表明,仅基于植株投影面积无法建立准确有效的多品种全生育期生物量测量模型[13]。通过加入其他表征因子,如绿色比[16]、株龄[17]、株高及分蘖数[18]等,可提高生物量测量模型的精度。然而,这些研究的对象大多为处于营养生长早期的少量品种,构建的模型品种及生育期适应性较差。另外,上述研究均基于传统的回归分析建模,不足以描述图像特征与生物量之间复杂的非线性关系。
自从HINTON等[19]开创性地提出深度信念网络以来,基于大数据驱动的深度学习技术以其优越的性能及充足的生理学基础而广泛地应用于各个领域[20-26]。深度学习的优势在于可以直接将原始数据输入到模型中,而不需要单独对特征进行选择与变换,由模型通过学习给出合适的特征表示[27]。从理论上来说,将原始图像输入深度学习网络即可得到很好的检测结果,但本研究中的原始图像尺寸非常大(2 452像素×2 056像素),现有网络无法处理,若直接压缩则会造成很多图像细节丢失。另外,即使压缩到适合现有网络的图像尺寸(如224像素×224像素),对于这么多的参数输入,需要更多样本(数十万甚至数百万)才能得到较好的效果。因此,本研究采用先提取图像特征、再建模的方式。深度信念网络(Deep belief network, DBN)首先对网络进行无监督预训练,然后通过反向传播(Back propagation,BP)算法对网络进行微调,尤其适用于有标签样本的数量有限情况下的学习问题。深度信念网络具备层次化特征学习与表达的能力,在探索分析输入、输出间复杂非线性关系上具有独特优势[28]。
图像特征和水稻生物量间具有复杂的非线性关系,深度信念网络是解决这一问题的有效工具。本研究使用深度信念网络进行生物量建模的另一个重要原因在于,研究中有大量无标签样本,而深度信念网络能充分利用无标签样本提高模型性能,是研究水稻生物量测量模型的有力工具。本研究首先通过图像分析从原始水稻图像中提取生物量相关图像特征,然后引入深度信念网络,构建适用于多品种水稻生殖生育期的水稻生物量模型。
1 材料与方法
1.1 成像系统
本研究中的图像采集装置如图1所示。水稻植株由工业输送线自动输送至检测区域,电动旋转台带动水稻旋转一周,由彩色工业相机(AVT Stingray F-504)采集水稻图像,图像尺寸为2 452像素×2 056像素。每盆植株每次采集14个不同角度下的可见光图像。采集到的图像将自动传输至工作站。
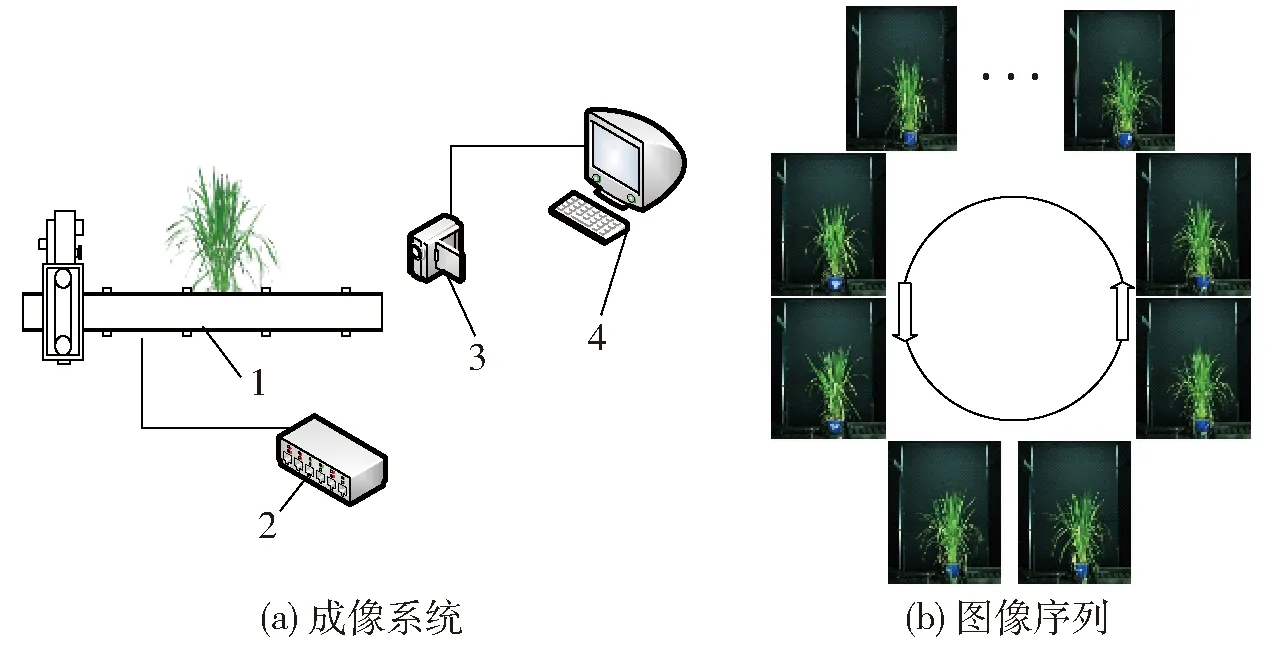
图1 图像采集装置Fig.1 Image acquisition equipment1.旋转台 2.控制器 3.相机 4.工作站
1.2 试验材料与图像采集
本研究的试验材料为存在广泛自然变异的483份水稻核心种质资源。样本种植于直径为22 cm的塑料盆中。试验设置对照组(N)和干旱胁迫组(D),每个组设置4个重复,共483×2×4=3 864个样本。对照组正常浇水,种植于露天环境下,而胁迫组种植在温室中,于孕穗期进行干旱胁迫。
当水稻样本长至孕穗期时,对胁迫组所有品种的4个重复采集图像。随后,胁迫组断水进行胁迫。采用TRIME-PICO32型土壤水分测量仪(IMKO Micromodultechnik GmbH, Ettlingen, 德国) 测量土壤含水率。当土壤含水率降至15%时,给胁迫组浇水,使土壤含水率保持在15%的水平5 d。再次采集胁迫组和对照组所有样本的水稻图像,并对胁迫组和对照组所有品种的两个重复进行有损人工测量获取水稻地上部分干物质量。复水后对胁迫组和对照组正常浇水,于成熟期进行第3次水稻图像采集,并对胁迫组和对照组所有品种的两个重复进行有损人工测量获取水稻地上部分干物质量。由于部分样本在测量中出现人为失误,最终具有人工测量干物质量数据的有标签样本为3 811个,仅有图像而无人工测量干物质量数据的无标签样本为3 829个。
1.3 图像处理及性状提取
1.3.1图像处理
图像采集完成后进行处理,主要步骤如下:①图像阈值分割。首先将图像转换到HSL颜色空间,利用HSL颜色空间固定阈值分割法分割图像,提取图像的L分量,设定阈值为100。去除小区域后得到水稻植株二值图像。②提取颜色分量。利用二值图像和原始RGB图像进行掩模操作,获取植株的RGB图像,提取水稻植株图像的超绿分量(GEx)和超红分量(REx),若某像素的GEx值大于预定义GEx阈值,REx值小于预定义REx阈值,则该像素被分割为植株绿色部分。提取i2组分,测定水稻植株的黄色部分。各颜色分量的计算公式为
(1)
(2)
(3)
GEx=2g-r-b
(4)
REx=1.4r-b
(5)
i2=0.5R-0.5B
(6)
式中R、G、B——彩色RGB图像的R、G、B分量
r、g、b——归一化R、G、B分量
③检测水稻植株边缘和最小外接矩形。利用IMAQ EdgeDetection VI提取水稻植株边缘,并利用IMAQ Particle Analysis VI检测水稻植株最小外接矩形(图2)。

图2 水稻植株边缘和最小外接矩形检测Fig.2 Detection of edge and border of rice plants
1.3.2图像特征提取
基于处理好的水稻图像,对每个植株共提取57个图像特征,分别为:
株高(HP):将水稻拉直后测量得到的高度。
分蘖数(NT):分蘖的数目。
绿色投影面积(AG):植株绿色部分的像素数。
茎秆面积(AST):茎秆像素数。
植株投影面积(A):植株像素数。
绿色比(RGLA):绿色投影面积与植株投影面积的比值。
植株密度(C1~C6):将图像分为若干个尺寸为5像素×5像素的子图像,计算每个子图像内的前景像素比例。像素点的密度定义为该像素点所在子图像中的前景像素数占子图像总像素数的比例。对植株180°范围的图像(本研究中为7幅)进行同样处理,以这些图像得到的密度均值作为植株密度。根据子图像内的前景像素比例,将子图像划分为6个不同水平,分别为水平1(0~10%)、水平2(10%~20%)、水平3(20%~40%)、水平4(40%~60%)、水平5(60%~80%)、水平6(80%~100%)。统计不同前景像素比例水平中所含子图像数占所有子图像数的比例,计算得到6个不同植株密度水平,分别记为C1、C2、C3、C4、C5、C6[29]。
周长面积比(RPA):植株周长与植株投影面积之比,其中周长为植株边缘像素的数目。
分形维数1(DF1):由植株原始图像计算得到的分形维数。
植株外接矩形高(H):植株最小外接矩形的高度。
植株外接矩形宽(W):植株最小外接矩形的宽度。
植株占空比(RPB):植株面积与其最小外接矩形面积的比值。
高宽比(RHW):植株外接矩形高与植株外接矩形宽的比值。
分形维数2(DF2):以植株最小外接矩形为边界裁剪图像后计算的分形维数。
深绿色面积(ADG):植株深绿色部分的前景像素数。
植株相对频数(F1~F14):本文共采集了植株360°旋转范围内的14幅图像,每幅侧视图对应不同的植株角度,侧视图中相同的像素点位置在不同的侧视角度下对应着不同的植株位置。统计侧视图像中每个像素点处出现前景像素(植株像素)的次数。本实验共14幅侧视图,即前景像素出现次数为0~14。不考虑前景像素出现次数为0的像素数,统计图像中出现i次前景像素的像素点的个数,根据统计的个数,计算出现i次前景像素的相对频率,得到14个分布频率特征,记为特征F1、F2、F3、F4、F5、F6、F7、F8、F9、F10、F11、F12、F13、F14[30]。
浅绿色面积(ALG):植株浅绿色部分的前景像素数。
绿色等级(GC):植株颜色等级分为深绿色和浅绿色,分别用1和0表示。当植株深绿色面积大于浅绿色面积时为1,否则为0。
直方图特征:均值M、标准差S、三阶矩MU3、平滑度R、熵E、一致性U[29]。
灰度-梯度共生矩阵特征T1~T15:T1、T2、T3、T4、T5、T6、T7、T8、T9、T10、T11、T12、T13、T14、T15分别为相关、小梯度优势、大梯度优势、能量、灰度分布不均匀性、梯度分布不均匀性、灰度平均值、梯度平均值、灰度熵、梯度熵、混合熵、差分矩、逆差分矩、灰度均方差、梯度均方差[30]。
表1为各时期57个特征的平均值及各特征与生物量之间的相关性。从表中可以看出,大多数特征与生物量之间具有极显著的相关性。
2 水稻生物量无损检测模型构建
2.1 数据预处理及性能评价
本研究中有标签样本3 811个,无标签样本3 829个,深度信念网络能充分利用无标签样本提高模型性能,是研究水稻生物量测量模型的有力工具。将有标签样本随机划分为训练集和测试集,其中训练样本3 000个,测试样本811个。为了消除不同水稻生物量特征数据量纲的差异,提高训练收敛速度,利用Matlab工具箱中的mapminmax函数将数据归一化至[0,1]区间。
本文采用决定系数R2(Coefficient of determination)、平均相对误差(Mean absolute percent error,MAPE)、相对误差绝对值的标准差(Standard deviation of absolute percent error,SAPE)来判断所构建模型的性能。计算公式为
(7)
(8)
(9)
式中VAPEi——第i个样本的相对误差绝对值
VMAPE——平均相对误差
VSAPE——相对误差绝对值的标准差
yai——第i个样本的生物量系统测量值
ymi——第i个样本的生物量人工测量值
n——样本数量
2.2 基于多元线性回归的水稻生物量模型构建
通过逐步线性回归法对水稻生物量数据进行回归分析,并通过方差膨胀因子(Variance inflation factor, VIF)进行共线性检验,当某个回归变量的VIF小于10时,认为建立的回归模型无显著的共线性。最终从57个特征值中筛选出4个特征值,并利用SPSS对其进行共线性检验,确定无共线性。最终构建的逐步线性回归模型方程为
Y=0.072+1.185X1-0.224X2-0.270X3-0.224X4
(10)
式中Y——植株干物质量
X1——三阶矩X2——株高
X3——茎秆面积
X4——植株外接矩形高
该模型测试集的R2为0.807 6、MAPE为22.15%、SAPE为37.53%。
2.3 基于深度信念网络的水稻生物量模型构建
线性回归模型的性能相对较差,为了提高模型性能,构建基于深度信念网络的生物量模型。
DBN模型训练中可见层数据类型、隐含层层数、隐含层节点数、学习率、迭代次数、动量都会对模型性能产生影响,本文分别测试其对DBN模型性能的影响。
(1)可见层数据类型
分别测试可见层数据类型为高斯型和概率型时对DBN模型性能的影响,结果表明高斯型模型的R2为0.925 9,MAPE为11.60%,SAPE为18.00%;概率型模型的R2为0.906 9,MAPE为14.51%,SAPE为33.18%,高斯型数据类型性能优于概率型。
(2)隐含层层数
DBN隐含层层数很大程度上影响着DBN模型的性能。选择5种不同DBN隐含层层数,分别测得它们对DBN模型性能的影响,结果如表2所示。当隐含层层数为3时,模型性能最优。
(3)隐含层节点数
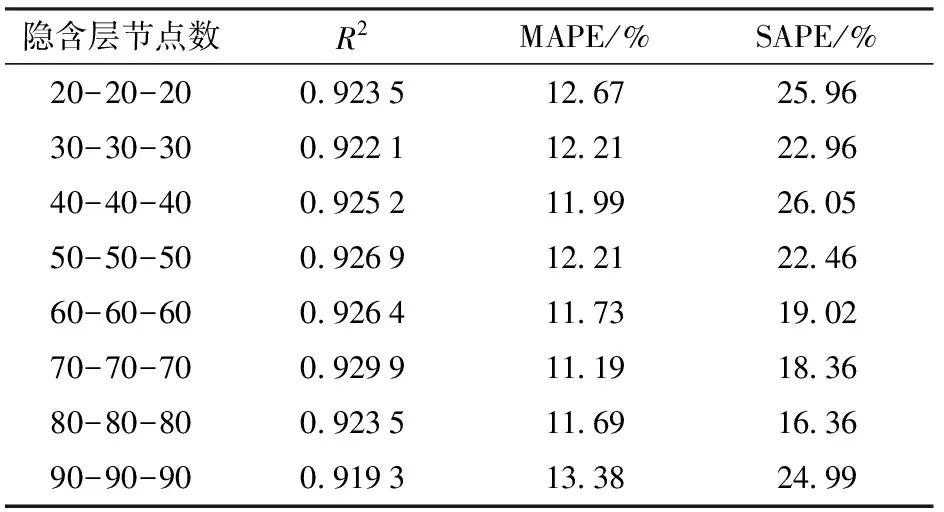
分别选择8种不同的隐含层节点数测试其对DBN模型性能的影响,结果如表3所示。从结果可以看出,隐含层节点数为70-70-70时,模型性能最优。
(4)学习率
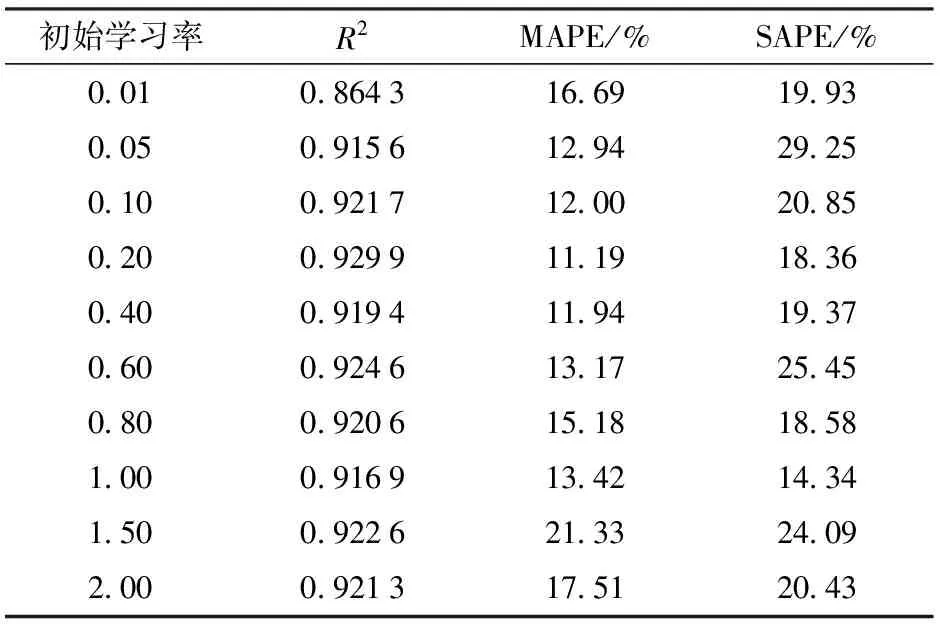
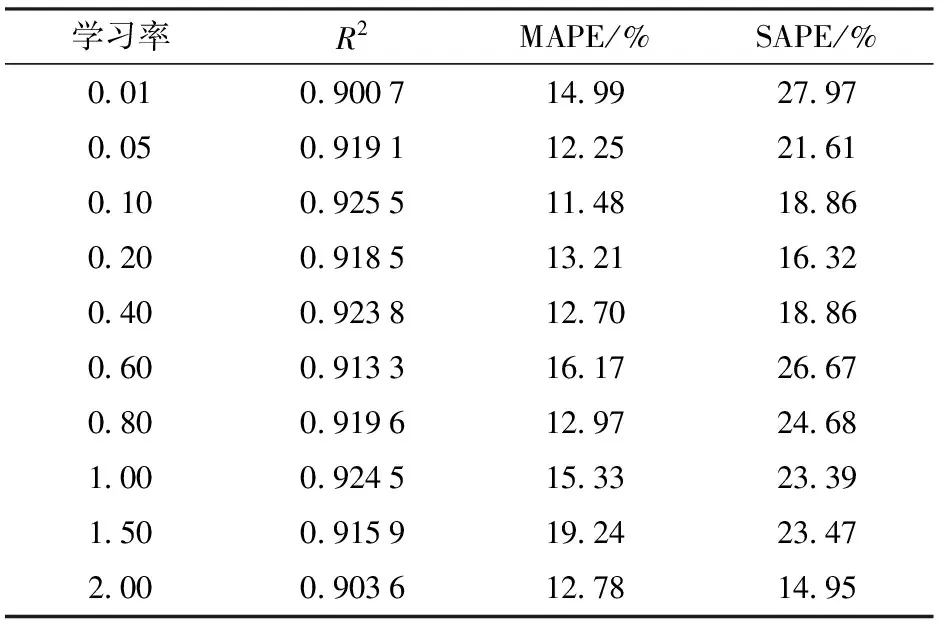
DBN训练中选择合适的学习率可以有效提高参数学习的收敛速度和学习性能。首先设置受限玻尔兹曼机(Restricted Boltzmann machines, RBM)预训练的学习率为0.1,然后测试BP算法不同学习率对DBN模型性能的影响。表4和表5分别为学习率随迭代次数改变(式(11))和不随迭代次数改变对模型性能的影响。结果显示,学习率随迭代次数改变且初始学习率为0.2时,DBN训练的精度高,建立的模型更准确。
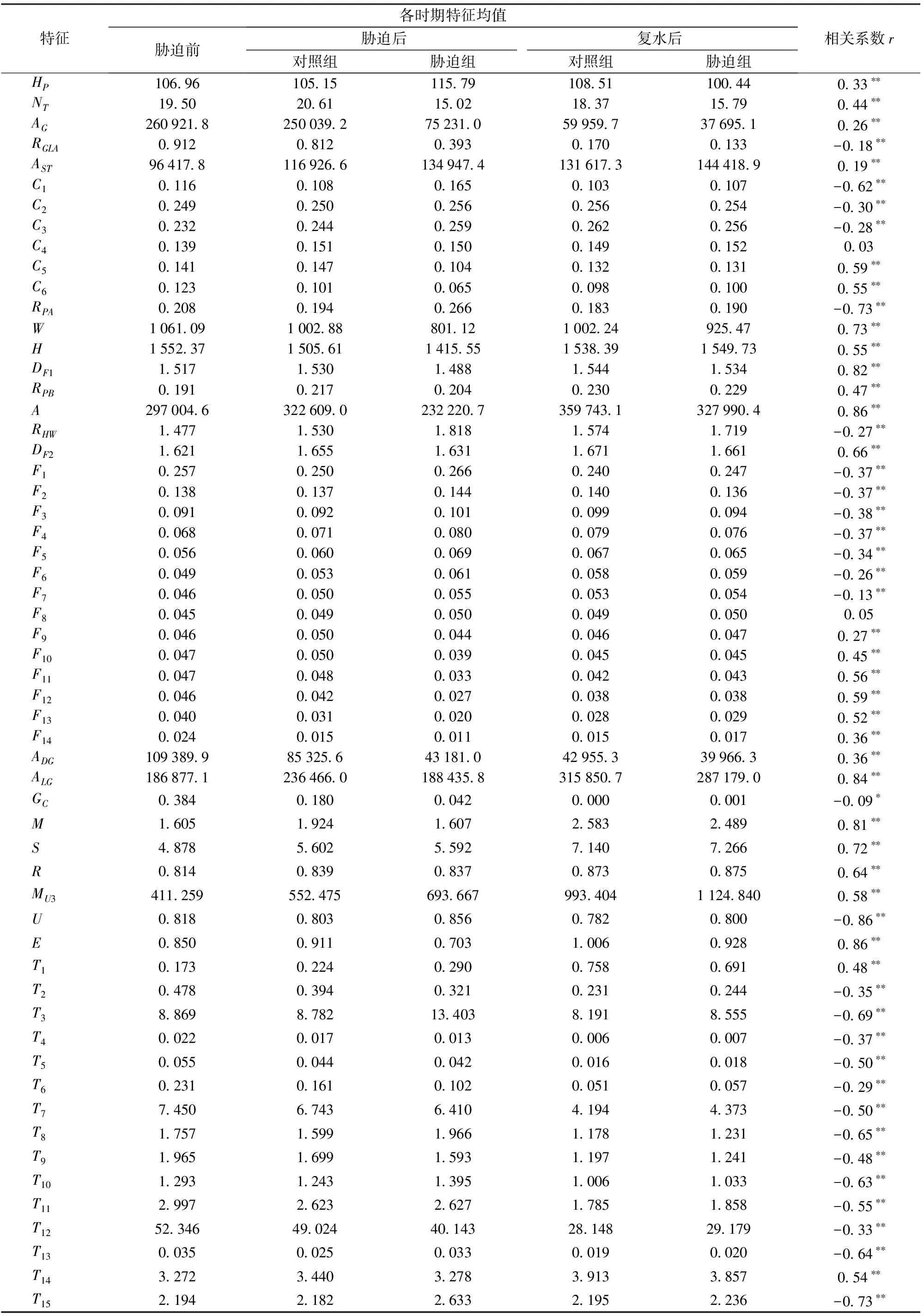
表1 各时期特征均值与生物量之间的相关性分析Tab.1 Correlation analysis of feature values for each period and biomass
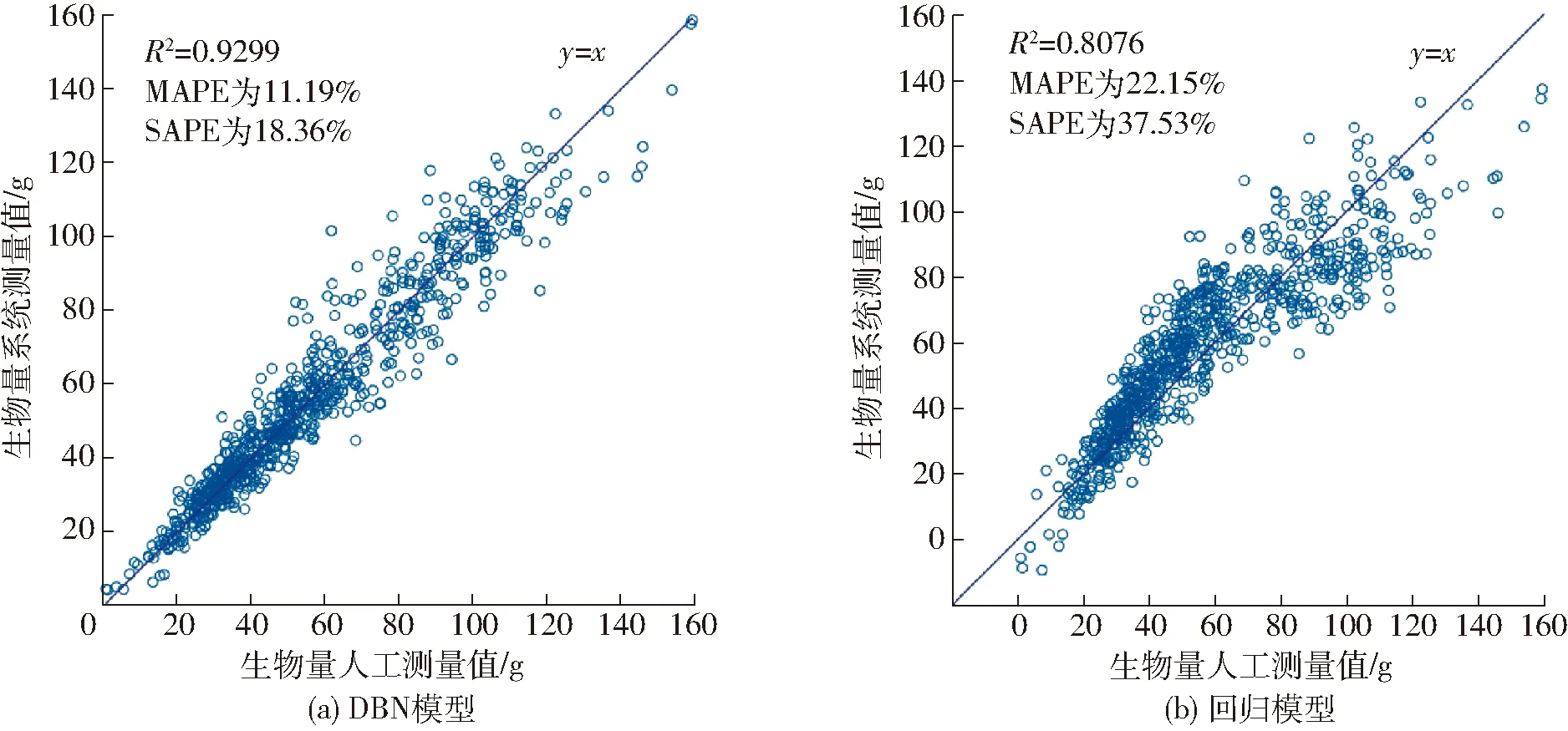
注:** 表示极显著(P<0.001);*表示显著(0.001 表2 隐含层层数对DBN模型性能的影响Tab.2 Influence of hidden layer number on performance of DBN model 表3 隐含层节点数对DBN模型性能的影响Tab.3 Influence of hidden layer neuron number on performance of DBN model (11) 式中li——迭代次数i时的学习率 l0——初始学习率 i——迭代次数 表4 DBN训练中学习率随迭代次数改变对DBN模型性能的影响Tab.4 Influence of learning rate which varied with change of iterations on performance of DBN model (5)迭代次数 迭代次数对模型性能有较大的影响。从迭代次 表5 DBN训练中学习率不随迭代次数改变对DBN模型性能的影响Tab.5 Influence of learning rate which did not vary with change of iterations on performance of DBN model 数50~2 000之间选择9种不同的迭代次数,分别测试其对DBN模型性能的影响,结果如表6所示。从表中可知,当DBN模型迭代次数为200时,模型性能最优。 表6 迭代次数对DBN模型性能的影响Tab.6 Influence of different numbers of iteration on performance of DBN model (6)动量 为了测试动量对性能的影响,分别测试了动量随迭代次数改变(式(12))和不随迭代次数改变对DBN模型性能的影响。结果表明,可变动量条件下DBN的R2为0.929 9,MAPE为11.19%,SAPE为18.36%;固定动量条件下DBN的R2为0.915 4,MAPE为12.70%,SAPE为23.34%。 (12) 式中mi——第i次迭代的动量 综上,最终确定了性能最优的DBN模型,即可见层数据类型为高斯型,隐含层层数为3层,隐含层节点数为70-70-70,学习率为0.2,迭代次数为200,动量随迭代次数改变而改变。 图3为DBN模型与回归模型对测试集处理性能比较的结果。 分析图3可知,DBN模型R2较线性回归模型增加了0.122 3,MAPE和SAPE分别降低了10.96个百分点和19.17个百分点,因此DBN模型具有更优的拟合效果。 图3 DBN模型及回归模型性能比较Fig.3 Comparison of performance between DBN model and regression model (1)对不同品种水稻核心种质资源进行图像采集,并利用HSL颜色空间固定阈值分割法分割图像,对处理后的图像进行特征提取,每个植株共获得57个水稻特征值。 (2)通过逐步线性回归方法构建水稻生物量回归模型,模型测试集的R2为0.807 6、MAPE为22.15%、SAPE为37.53%。 (3)通过反复试验构建一组可见层数据类型为高斯型、隐含层层数为3、隐含层节点数为70-70-70、学习率为0.2、迭代次数为200的多品种生物量无损检测DBN模型,模型测试集R2为0.929 9,MAPE为11.19%,SAPE为18.36%。 (4)将回归模型与DBN模型的性能进行对比,结果表明,DBN模型具有更优的训练结果。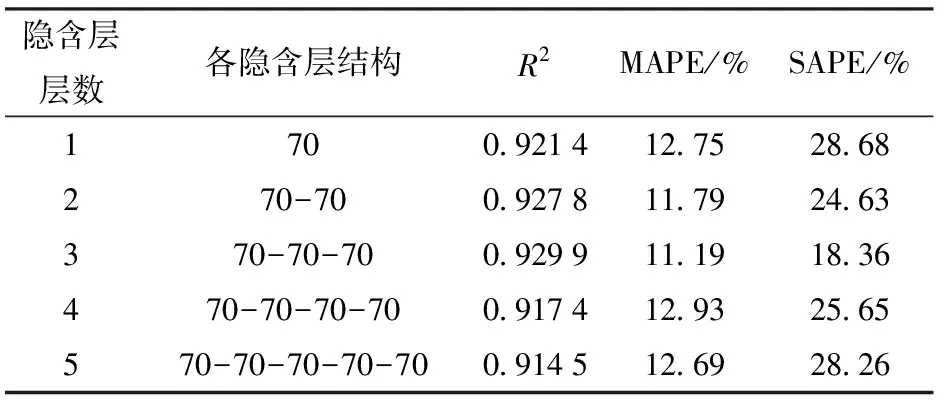

2.4 DBN模型与回归模型性能比较
3 结论
