基于启发式动态规划的履带机器人路径跟随控制方法

宋 彦 张羊阳 姚 琦 袁 胜 廖 娟 刘 路

(1.安徽农业大学工学院， 合肥 230036; 2.安徽省智能农机装备工程实验室， 合肥 230036;3.合肥中科智驰科技有限公司， 合肥 230088)

0 引言

随着移动机器人在农业领域的广泛应用，复杂的地形和多变的环境对移动机器人的运动控制能力提出了更高的要求，如何提高移动机器人在未知、复杂环境的路径跟随性能成为研究的热点。

路径跟随的控制机理多采用“预瞄—跟随”原理[1-2]，传统的控制方法有纯追踪[3]和PID控制[4-5],但是上述方法均忽略了系统的数学模型，难以取得高精度的控制效果。一些学者提出了基于车辆动力学模型[6]或运动学模型[7]的控制方法，例如：基于期望横摆角速度[8]以及横向速度[9]的状态反馈控制方法，基于模型预测控制[10-11]的方法等。此类方法在模型较为精确的条件下，提高了控制精度，但是需要调节和优化的控制参数较多，尤其是当机器人的工作环境发生变化时，需要重新选择控制参数，优化控制性能。

近年来，如何提高移动机器人的环境适应性和自主行为能力成为学界的研究热点，出现了基于智能控制的方法[12-13]，如基于模糊控制[14-15]和神经网络方法[16]等，如文献[17]采用模糊控制理论调整前视距离，文献[18]提出了一种自适应模糊变结构控制方法。但上述方法仍然需要将专家经验抽象为模糊控制规则，并调校模糊控制参数。文献[19]提出了一种根据车辆速度和道路弯度动态调整预瞄距离的改进纯追踪方法。也有学者采用了一些智能优化算法，如文献[20]采用了遗传算法自动优化控制参数，文献[21]提出了一种基于增量Q学习的控制参数优化方法。

自适应动态规划[22](Adaptive dynamic programming, ADP)理论采用了强化学习机制，通过计算环境对不同策略的评价性反馈信号来优化控制策略，使智能体具备了自主优化能力[23]。ADP理论包含了不同的实现方法，如启发式动态规划(Heuristic dynamic programming, HDP)、对偶启发式规划(Dual heuristic programming, DHP)等。ADP理论的实现框架有执行器、评价器两个模块，评价器基于性能指标函数评价当前控制动作的性能优劣，执行器根据评价结果优化控制动作，并通过“执行—评价”迭代运算寻找最优控制策略。近年来，这一方法被用于过程控制、机器人控制等领域。文献[24]提出了一种基于回声状态网络的HDP控制方法，用于污水处理过程控制。在移动机器人的应用领域，文献[25]提出了一种基于HDP的路径规划方法。文献[26]较早地将ADP理论应用于移动机器人的路径跟踪控制问题，但是其建立的回报函数仅考虑了速度误差，且未对该方法进行试验验证。文献[27]采用一种基于DHP的方法用于机器人的路径跟随控制，该方法能够估计性能指标函数的导数，但是仍然缺乏相关的试验验证。

为提高移动机器人路径跟随控制方法对环境的适应性和自主优化能力，本文提出一种基于HDP算法的路径跟随控制方法，构建综合跟随精度指标和稳定性指标的回报函数，采用神经网络模型逼近评价器和执行器，通过开展对不同线形路径的跟随试验，验证该方法对未知路径线形的适应性。

1 控制系统结构与数学模型

1.1 控制系统结构

本文研究对象为履带式机器人，其路径跟随控制系统结构如图1所示，其中参考路径为一系列离散的GPS坐标，机器人通过车载GPS传感器得到实际位姿。坐标转换模块的功能是通过当前实际位姿和预瞄点信息得到位姿误差信息。路径跟随控制器根据位姿误差由控制算法计算产生控制动作。控制量转换模块将控制动作转换为两侧电机的转速，驱动机器人稳定跟随参考路径。

图1 控制系统结构Fig.1 Control system structure

1.2 系统数学模型

图2 履带机器人路径跟随示意图Fig.2 Tracked robot path following diagram

本文建立的履带机器人路径跟随示意图如图2所示，首先定义大地坐标系为XOY，其中X轴为正东方向，Y轴为正北方向。定义机器人局部坐标系为xoy，其中x轴方向为机器人前进方向，将y轴方向定义为机器人的前进方向逆时针旋转90°。其中L为预瞄距离，(Xc,Yc)为移动机器人在全局坐标系中的位置坐标，φc为车辆纵轴线与大地坐标系横坐标的夹角，(Xc,Yc,φc)定义为机器人的当前位姿。(Xp,Yp)为预瞄点在全局坐标系中的位置坐标，φp为预瞄点处的切线与大地坐标系横坐标的夹角，(Xp,Yp,φp)定义为预瞄点处的期望位姿。

在不考虑履带滑动的情况下，定义履带机器人的驱动轮半径为rd，履带中心距为B，当前机器人前进速度为vc，角速度为ωc，两侧电机的转速为nL、nR，vc和ωc与两侧电机转速的转换关系为

(1)

则履带式机器人的运动学模型可表示为

(2)

移动机器人相对预瞄点的误差状态方程为

(3)

式中xe——纵向偏差

ye——横向偏差

φe——航向角偏差

根据图2的几何关系，由式(2)、(3)可得移动机器人相对预瞄点Op的横向偏差和航向角偏差的变化率为

(4)

式中ω——横摆角速度

vx——移动机器人纵向速度

vy——移动机器人横向速度

ρ——预瞄点处的道路曲率

2 基于HDP算法的路径跟随控制策略设计

首先采用马尔可夫决策过程(Markov decision process, MDP)模型描述移动机器人路径跟随控制问题，然后采用HDP算法求解该控制问题的近似最优控制策略，并给出算法的实现框架，最后推导路径跟随控制器参数的在线学习规则。

2.1 路径跟随控制问题的MDP模型

ADP算法[28]的理论框架是以马尔可夫决策过程(MDP)为基础的。一个MDP模型由四元组{S,U,r(s,u,s′),P(s,u,s′)}表示，其中S为状态集合，U为动作集合，r(s,u,s′)为机器人采用动作u使其从状态s转移到s′时获得的回报，P(s,u,s′)为机器人采用动作u使其从状态s转移到s′时的概率。

针对路径跟随问题，选取状态s=(ye,φe,ωc,ρ)T，动作u=ω。由式(4)离散化后可以得到状态转移方程为

(5)

式中Ts——系统的控制周期

基于MDP模型，将路径跟随最优控制策略描述为：寻找合适的控制动作u使得机器人从状态s(k)转移到s(k+1)，且使得性能指标函数最小。性能指标函数公式为

(6)

式中E()——数学期望

rt——t时刻的回报

γ——折扣因子

路径跟随过程中，不但期望减小横向偏差，也期望尽量减少控制动作波动，因此选取的回报函数为

r(s(k),u(s(k)))=
s(k)TQs(k)+(u(s(k))-ωp)TR(u(s(k))-ωp)

(7)

其中

ωp=vxρ

式中Q——半正定对角矩阵，表征对横向偏差和航向角偏差指标的权重

R——正常数，表征对期望横摆角速度补偿的权重

2.2 路径跟随控制器设计

本文定义的性能指标函数式(6)也可描述为

J(s(k))=r(s(k),u(s(k)))+γJ(s(k+1))

(8)

根据Bellman优化原理，最优的控制策略为

(9)

定义u*(s(k))为使性能指标函数极小化的最优控制动作，式(8)可以写作

J*(s(k))=r(s(k),u*(s(k)))+γJ*(s(k+1))

(10)

式中J*(s(k))——最优性能指标函数

J*(s(k+1))——机器人在下一状态s(k+1)时的最优性能指标函数

令∂J*(s(k))/∂u*(s(k))=0，则最优控制动作可表示为

(11)

为实现上述最优控制，构建如图3所示基于HDP算法的控制框架。算法实现通常包括3部分[21]：评价器、模型以及执行器，评价器的作用为根据状态变量估计性能指标函数J(s(k))的值；执行器的作用为根据状态变量计算控制动作u(s(k))；模型对移动机器人下一状态s(k+1)进行预测。评价器1和评价器2的结构及参数均相同，但是分别用于估计当前状态的性能指标函数值以及预测状态的性能指标函数值。为了按照时间正向求解控制动作，HDP方法往往采用函数近似的方法估计性能指标函数值[21]，本文采用多层前馈神经网络逼近评价器，同样也采用这一模型逼近最优动作。算法执行过程中，采用梯度下降算法依次对动作网络和评价网络里的神经网络权值进行反馈调节，最小化性能指标函数J(s(k))，进而获得使J(s(k))最优的控制策略u(s(k))。

图3 基于HDP算法的路径跟随控制方法结构图Fig.3 Structural diagram of path following control method based on HDP algorithm

2.3 控制器参数的在线学习

控制器参数在线学习过程实质上是对神经网络权值的在线调整过程，其目标是寻求一组最优权值使J(s(k))最小化，进而获取近似最优控制动作。HDP算法中评价器网络的优化目标是对最优性能指标函数值的近似，执行器网络优化的目标是找到最优控制动作u*(s(k))使得目标函数J(s(k))最小。

本文采用3层前馈神经网络实现评价器和执行器，激活函数为Sigmoid函数，从隐含层到输出层的函数为线性函数，此时执行器和评价器的表达式分别为

u(s(k))=Φa(Waσa(Vas(k)+ba1)+ba2)

(12)

Jc(s(k))=Φc(Wcσc(Vcs(k)+bc1)+bc2)

(13)

式中Jc(s(k))——评价器对状态s(k)估计的性能指标函数值

Va、Vc——神经网络从输入层到隐含层的权值

ba1、bc1——神经网络从输入层到隐含层的偏置

Wa、Wc——神经网络从隐含层到输出层的权值

ba2、bc2——神经网络从隐含层到输出层的偏置

σa、σc——Sigmoid函数

Φa、Φc——线性函数

2.3.1执行器网络参数优化

执行器的学习目标是最小化误差函数

(14)

定义ζd(k)=u(s(k))-u*(s(k))，则执行器网络的权值和偏置更新规则为

(15)

其中

Ψa(k)=(Wa,ba2,Va,ba1)

式中αa(k)——执行器网络的学习率

Ψa(k)——执行器网络的权值和偏置

由式(12)可得

(16)

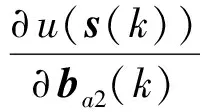
(17)

(18)

(19)

其中

σ′a(x)=e-x/(1+e-x)2

式中σ′a(x)——Sigmoid函数导数

2.3.2评价器网络参数优化

定义误差

δd(s(k))=Jc(s(k))-r(s(k),u(s(k)))-
γJc(s(k+1))

(20)

式中Jc(s(k+1))——评价器对状态s(k+1)估计的性能指标函数值

因此评价器网络的学习目标是最小化误差函数

(21)

则评价器网络的权值和偏置更新规则如下

(22)

其中

Ψc(k)=(Wc,bc2,Vc,bc1)

式中αc(k)——评价器网络的学习率

Ψc(k)——评价器网络的权值和偏置

由式(13)可得

(23)

(24)

(25)

(26)

其中

σ′c(x)=e-x/(1+e-x)2

式中σ′c(x)——Sigmoid函数导数

3 仿真分析

为了验证本文提出算法的有效性，在Matlab/Simulink环境下，通过数值仿真验证该方法的性能。定义跟随轨迹点到参考路径的垂线距离为横向偏差，采用横向偏差平均值的绝对值和横向偏差的均方根值评价跟随性能。

仿真参数设置为：机器人履带中心距0.485 m，驱动轮半径0.2 m，控制周期Ts=0.2 s。为了对比控制效果，同时设计了基于LQR和基于传统纯追踪算法的控制器，并且在不同速度下对3种控制器进行仿真。参考路径采用了组合线(直线和圆)和螺旋线。

为了观察误差收敛过程，将机器人的起点偏离轨迹起点一段距离，在跟随组合线时，组合线起点为(0 m,-20 m)，机器人的起点为(2 m,-20 m)。当速度v=0.3 m/s时，LQR算法和纯追踪算法的预瞄距离为2.5 m，HDP算法的预瞄距离为3 m。选取LQR算法的反馈矩阵K=[-0.15 -0.02]T，HDP算法的参数为Q=diag{4,1,0,0}，R=1，γ=0.9，学习步长为0.2。基于纯追踪算法、HDP算法以及LQR算法的路径跟随轨迹如图4所示，对应的横向偏差如图5所示。为准确评价其跟随误差，剔除初始误差的收敛过程，分析机器人进入稳态跟随时的横向偏差，结果如表1所示。

在螺旋线的参考路径中，螺旋线可表示为

(27)

螺旋线的起点为(53 m,-29 m)，也将机器人的起点偏离轨迹起点，设定为(53 m,-27 m)。基于纯追踪算法、HDP算法以及LQR算法的路径跟随轨迹如图6所示，对应的横向偏差如图7所示。表2为剔除初始误差的收敛过程，进入稳态跟随状态后的误差统计结果。

图4 速度为0.3 m/s时不同控制器跟随组合线的轨迹Fig.4 Trajectory of robot using different controllers on combination line at speed of 0.3 m/s

图5 速度为0.3 m/s时不同控制器跟随组合线的横向偏差Fig.5 Lateral error of different controllers on combination line at speed of 0.3 m/s

表1 速度为0.3 m/s时不同控制器跟随组合线的误差Tab.1 Tracking error of different controllers on combination line at speed of 0.3 m/s m

图6 速度为0.3 m/s时不同控制器跟随螺旋线的轨迹Fig.6 Trajectory of robot using different controllers on helical line at speed of 0.3 m/s

图7 速度为0.3 m/s时不同控制器跟随螺旋线的横向偏差Fig.7 Lateral error of different controllers on helical line at speed of 0.3 m/s

评价参数纯追踪算法LQR算法HDP算法平均误差绝对值0.020.030.01均方根误差 0.090.070.02

为了验证移动机器人在不同速度下的跟随效果，改变机器人移动速度v=1 m/s进行仿真。LQR算法、纯追踪算法以及HDP算法的预瞄距离均为3 m。选取LQR算法的反馈矩阵K=[-0.3 -0.005]T,HDP算法参数不变，纯追踪算法的预瞄距离不变，机器人起点不变。基于纯追踪算法、HDP算法以及LQR算法的路径跟随轨迹如图8所示，对应的横向偏差如图9所示。表3为剔除初始误差的收敛过程，进入稳态跟随状态的误差统计结果。

图8 速度为1 m/s时不同控制器跟随组合线的轨迹Fig.8 Trajectory of robot using different controllers on combination line at speed of 1 m/s

图9 速度为1 m/s时不同控制器跟随组合线的横向偏差Fig.9 Lateral error of different controllers on combination line at speed of 1 m/s

在跟随螺旋线时，机器人起点不变。基于纯追踪算法、HDP算法以及LQR算法的路径跟随轨迹如图10所示，对应的横向偏差如图11所示。表4为剔除初始误差的收敛过程，进入稳态跟随状态的误差统计结果。

从仿真结果可以得出，3种控制算法在2种跟随速度条件下，均能够实现对两种复杂线形的跟随控制，设置的初始误差均得到快速收敛。在跟随组合线时，3种控制方法的稳态平均误差绝对值均在0附近，基于HDP控制方法的均方根误差比纯追踪算法和LQR算法要小。组合线曲率在直线与半圆线交接处、两条半圆曲线交接处均发生了变化，虽然基于HDP算法在此时的瞬态误差较大，但随即收敛到0附近，而纯追踪算法和LQR算法，在跟随半圆线时，误差基本不变。在跟随螺旋线时，可以看出随着螺旋线曲率的增大，3种控制算法的横向偏差均有增大的趋势，但是基于HDP算法的平均误差绝对值依然比纯追踪算法和LQR算法小，基于HDP算法的均方根误差小于或等于基于纯追踪算法和LQR算法的均方根误差。上述现象说明，相对于其他两种方法，HDP算法可以通过参数的在线学习，自主优化路径跟随性能，减小控制误差。

表3 速度为1 m/s时不同控制器跟随组合线的误差Tab.3 Tracking error of different controllers on combination line at speed of 1 m/s m

图10 速度为1 m/s时不同控制器跟随螺旋线的轨迹Fig.10 Trajectory of robot using different controllers on helical line at speed of 1 m/s

图11 速度为1 m/s时不同控制器跟随螺旋线的横向偏差Fig.11 Lateral error of different controllers on helical line at speed of 1 m/s

表4 速度为1 m/s时不同控制器跟随螺旋线的误差Tab.4 Tracking error of different controllers on helical line at speed of 1 m/s m

4 试验结果分析

4.1 路径跟随试验结果

本文使用的履带机器人试验平台如图12所示，其长度为0.8 m，宽度为0.57 m，质量约为60 kg，履带中心距B为0.485 m，驱动轮半径rd为0.2 m。采用48 V、20 A·h的锂电池供电，驱动电机功率为400 W。传感器为北斗星通BDM680，工作在差分定位模式，移动站与基准站之间的距离小于5 km，位置类型状态为Narrow_Int，按照产品手册，在该工作模式下定位误差为0.01 m(RMS)，通过双天线定位提供移动平台的航向角信息。计算平台采用工控机和基于STM32单片机的控制卡组成，工控机计算控制动作；单片机控制卡通过数学模型将控制动作分解为两侧履带转速，并给电机驱动器发送指令。

图12 履带机器人Fig.12 Tracked robot

试验路径包括了直线、钝角转向曲线以及锐角转向曲线，试验地点为安徽农业大学农萃园。机器人运动速度v=0.3 m/s，系统控制周期Ts=0.5 s。为验证HDP算法的路径跟随性能，同时采用LQR算法和纯追踪算法作为比较。为了获得对不同线形的理想跟随效果，对LQR算法和纯追踪算法的控制参数作了针对性调试。为了验证HDP算法对不同线形的自适应能力，在跟随不同的参考路径时，不改变HDP算法的参数配置，其参数配置为Q=diag{2,1,0,0}，R=5，γ=0.9，控制器的神经网络隐含层的神经元均为5个，学习步长均为0.2。采用基于LQR算法获得的路径跟随数据训练评价器和执行器网络，获得初始网络权值。

在跟随直线时，3种方法的预瞄距离均为3 m，其中LQR算法的反馈矩阵K=[-0.11 -0.015]T。图13为3种方法跟随直线轨迹。图14为不同控制器跟随直线的横向偏差，其误差统计量如表5所示。

图13 基于不同控制器跟随直线的轨迹Fig.13 Trajectory of robot using different controllers on straight line

图14 基于不同控制器跟随直线的横向偏差Fig.14 Lateral error of different controllers on straight line

m

在跟随钝角转向曲线时，纯追踪算法的预瞄距离为2.5 m，LQR算法为3 m，其中LQR算法的反馈矩阵K=[-0.05 -0.055]T。图15为3种方法跟随钝角转向曲线的轨迹，图16为不同控制器跟随钝角转向曲线的横向偏差，其统计量如表6所示。

在跟随锐角转向曲线时，预瞄距离均为3 m，其中LQR算法的反馈矩阵K=[-0.25 -0.075]T。图17为3种方法跟随锐角转向曲线的轨迹，图18为不同控制器跟随锐角转向曲线的横向偏差，其统计量如表7所示。

图15 基于不同控制器跟随钝角转向曲线的轨迹Fig.15 Trajectory of robot using different controllers on obtuse angle steering curve

图16 基于不同控制器跟随钝角转向曲线的横向偏差Fig.16 Lateral error of different controllers on obtuse angle steering curve

图17 基于不同控制器跟随锐角转向曲线的轨迹Fig.17 Trajectory of robot using different controllers on acute angle steering curve

图18 基于不同控制器跟随锐角转向曲线的横向偏差Fig.18 Lateral error of different controllers on acute angle steering curve

4.2 结果分析

总结上述试验结果可以发现，3种方法均能够顺利跟随直线、钝角转向曲线以及锐角转向曲线。对比LQR和纯追踪算法，在跟随直线时， HDP算法除均方根误差等于LQR算法的同类指标外，其他统计指标均为最小；在跟随钝角转向曲线时，HDP算法除最大误差绝对值略大于LQR算法同类指标0.03 m，其余两项误差指标均最小；在跟随锐角转向曲线时，HDP算法除平均误差绝对值略大于LQR算法同类指标0.01 m，其余两项误差指标均最小。为了完成3种曲线的路径跟随任务并取得较好的控制效果，试验过程中对纯追踪算法和LQR算法都进行了反复参数优化。而HDP算法仅通过历史跟随数据对评价器和执行器网络进行了离线训练，变换跟随路径时控制参数未做人工调试，仅通过HDP算法的参数优化机制对控制网络进行在线优化，即可取得较高精度的跟随结果，说明该方法具有较好的自主优化能力。

表7 不同控制器跟随锐角转向曲线试验的误差Tab.7 Tracking error of different controllers on acute angle steering curve m

5 结论

(1)针对移动机器人传统路径跟随控制算法环境适应能力弱、需要人工优化控制参数的问题，以履带式移动机器人为研究对象，提出了一种基于启发式动态规划的路径跟随控制方法，并试验验证了路径跟随性能，结果表明，跟随直线的均方根误差为0.06 m，跟随钝角转向曲线的均方根误差为0.06 m，跟随锐角转向曲线的均方根误差为0.09 m。该方法可以实现对多种复杂线形的路径跟随，且具有较高的控制精度。

(2)基于启发式动态规划算法框架，构建了综合跟随精度指标和稳定性指标的评价函数，通过对当前控制动作的评价性反馈信号优化控制器参数，仿真和试验结果表明，在跟随路径线形变化时，该方法不需要对控制参数进行调试，仅通过HDP算法的参数优化机制对网络权值进行在线优化就能够获得高精度的控制效果，具有较好的环境适应性和自主优化能力。