混凝土排桩深度优化及隔振效果研究

刘晶磊,赵晓玉,张瑞恒,刘 航,李 凯

(1.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000;2.河北建筑工程学院土木工程学院，河北 张家口 075000)

随着现代工业的迅速发展，城市化进程日益加快，由城市轨道交通引发的环境振动问题受到了普遍关注[1-3]。对由交通荷载引发的振动及其相应隔振屏障的研究已成为国内外学者研究的重要课题。如杨先健等[4]提出在地基土中设置隔振屏障可有效治理环境振动污染;Woods[5]通过对非连续隔振屏障的研究，发现单排桩隔振屏障的桩径大于被屏障波长的1/6时，才能保证隔振屏障取得较好的隔振效果；Andersen等[6]通过对空沟与填充沟的研究，发现空沟是最有效的隔振屏障，同时将空沟与排桩进行组合的联合波障比单独使用某一隔振屏障的效果更佳；Hayakawa等[7]通过对振动波的发生机理与传播规律的研究，提出了环境振动水平的预测方法；Aviles等[8-9]通过研究刚性桩和柔性桩对SH波的散射作用，发现刚性桩的隔振效果更优；时刚等[10]采用半解析边界元法对饱和土体中单排桩远场隔振效果进行了研究，发现增加桩长、桩径和桩身剪切模量能有效提高排桩的隔振效果；刘晶磊等[11]采用有限元模拟与现场模型试验相结合的方法对混凝土异形桩的隔振效果进行了研究，发现异形桩空心率是影响其隔振效果的重要因素；巴振宁等[12]考虑轨道及成层地基影响的情况，采用2.5维间接边界元方法研究了隔振沟对地基振动的隔振效果，发现不同地基模型、隔振沟深度及隔振沟距轨道距离都会对其隔振效果产生影响；肖世伟等[13]通过使用无限元及黏弹性边界建立空沟隔振有限元模型，研究了空沟深度、宽度以及荷载频率等对其隔振效果的影响；陈洪运[14]通过模型试验研究了桩间净距与排间净距对轨道交通路基段隔振效果的影响，发现桩距固定为1.5倍桩径、排距为2.5倍桩径时其隔振效果最佳；刘晶磊等[15]对单排微型混凝土桩隔振效果的敏感因素进行了现场试验研究，发现桩体长度对其隔振效果的影响较为明显；毕全超等[16]通过对空沟、填充沟隔振效果的研究，发现空沟的隔振效果优于填充沟；夏唐代等[17]通过研究不同形式的屏障对入射波SV波的隔振效果，发现非连续空心管桩屏障的隔振效果随桩间距的减小而提高，该研究结果可为非连续屏障的设计提供依据。

上述研究成果均验证了各类隔振屏障在环境振动污染治理中起到了良好的效果，并研究了隔振屏障的隔振因素对隔振效果的影响，但对于隔振屏障参数定量优化的研究较少。因此，本文以单排非连续混凝土桩为研究对象建立相应的无限元边界的有限元分析模型，通过建立振动波波长与混凝土排桩深度的关系，对多种变量下的混凝土排桩深度进行优化，并分析不同变量对混凝土排桩隔振效果的影响，为隔振工程建设提供有益参考。

1 有限元模型建立及波长分析

1.1 建立有限元分析模型

1.1.1 模型尺寸及边界设定

本文采用三维有限元模型对混凝土排桩的隔振效果进行分析研究，其路基边坡横断面图见图1。

图1 路基边坡横断面图(单位：m)Fig.1 Section diagram of subgrade 注：图中1∶m表示路基边坡的坡度。

模型以弹性半空间理论为基础，在模型四周及底部设置20 m厚的无限元边界(CIN3D8无限元单元)，防止固定边界产生的振动波反射；其余部分使用C3D8R三维应力单元，其厚度为20 m，模型整体厚度60 m。建立的有限元分析模型见图2。

图2 有限元分析模型Fig.2 Finite element analysis model

1.1.2 模型材料参数

本文采用弹性模型进行分析，模型材料参数见表1。

振动波在传播过程中，由于几何阻尼和材料阻尼的存在，致使振动波随着传播距离的增大，振动幅度逐渐减小，振动能量逐渐降低。所谓几何阻尼是指振动波随着其传播距离和范围的不断扩大，单位体积内的振动能量逐渐减小，从而使振动波所携带的能量被逐渐消耗。材料阻尼则是指传播介质自身有一定的阻尼作用，会吸收振动波的部分能量。其中，几何阻尼不需要设定材料参数，而材料阻尼需要设定材料参数，故将土体的质量阻尼系数α设定为0.406，其刚度阻尼系数β设定为0.072，而将混凝土桩的质量阻尼系数α设定为0.112，其刚度系数β设定为0.020。

表1 模型材料参数Table 1 Model material parameters

1.1.3 列车荷载条件

在列车行驶过程中，可将其产生的振动波近似看作是一个静荷载及一个动荷载组成的简谐振动荷载，其振动表达式为

F(t)=P0+P1sin(ω1t)

(1)

式中:P0为车轮静载(kN),P0=100 kN;t为荷载的作用时间(s)；P1为钢轨圆频率ω1对应的振动荷载峰值(kN),其表达式为

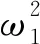
(2)

其中：α1为与钢轨圆频率对应的振动波振幅(mm)，不同频段振动波振幅α1见表2；M0为列车簧下质量(kg)，M0=750 kg；ω1为圆频率(rad/s)，其表达式为

ω1=2πf

(3)

其中：f为振动波频率(Hz)。

表2 不同频段振动波振幅α1Table 2 Vibration amplitude α1 in different frequency bands

取10 Hz、50 Hz、120 Hz振动波频率分别代表低频、中频、高频，以距路基边坡12.0 m处为测点，得到其地表振动波竖向加速度值分别为0.023 1 m/s2、3.83×10-5m/s2、1.23×10-6m/s2。由此可知：同低频振动相比，中、高频振动的衰减速度快，且中、高频振动对四周环境的影响也不如低频振动的剧烈。因此，本文采用低频(10 Hz)激振力函数F(t)来描述列车荷载条件，其表达式为

F(t)=100+10.35sin(62.8t)

(4)

1.1.4 评价标准

本文采用地表振动波振幅降低比Ar作为评价混凝土排桩隔振效果的标准，Ar数值越小其隔振效果越好[2]。其表达式为

(5)

式中：a1为设置排桩隔振后的地表振动波竖向加速度值(m/s2)；a0为无排桩隔振情况下地表振动波竖向振动加速度值(m/s2)。

1.2 混凝土排桩隔振效果区域分析及测点选取

在本次数值模拟过程中，选取距离混凝土排桩后3.0 m、6.0 m、9.0 m及12.0 m 4个测点的数据进行了分析，发现4个测点所表现的隔振规律性基本一致，故其中某一测点的隔振规律同样适用于其他3个测点。为了客观地反映混凝土排桩的隔振效果，需从上述4个测点中选取较为合理的位置作为测点,将设置排桩隔振后的地表振动波竖向加速度与无排桩隔振情况下的地表振动波竖向加速度进行对比，经计算得到混凝土排桩各测点的地表振动波振幅降低比Ar，从而作出其Ar等值线图，见图3。其中，振动波振动频率选取为10 Hz，排桩深度为10 m，布置于距路基边坡距离5.0 m处，排桩截面尺寸均为1.0 m×1.0 m，排桩间距为1.0 m。

图3 混凝土排桩隔振各测点的地表振动波振幅 降低比Ar等值线图Fig.3 Contour map of the amplitude reduction ratio of ground vibration wave Ar vibration isolation of concrete row piles at the monitoring points

由图3可见，由于排桩屏障的存在，改变了部分振动波的传播路径，其所产生的反射波与原振动波相互叠加干涉，混凝土排桩与路基边坡之间大部分区域地表振动波振幅降低比Ar值大于1.0；混凝土排桩布置区域后很小一部分区域地表振动波振幅降低比Ar值小于0.5，这是由于桩后很小一部分区域以透射波影响为主，受衍射波及散射波的影响较小；混凝土排桩布置区域后大部分区域受衍射波及散射波的影响，其Ar值处于0.5～0.7之间；在8.0～10.0 m之间的区域Ar值以0.7～0.9之间为主，为绕射波汇聚区域之一，使振动波一定程度上增强；在桩后一倍波长左右的位置，会出现较为明显的振动波增强点，其中心位置Ar值达到1.0以上。为客观地反映混凝土排桩的隔振效果，测点位置的选取需避开绕射波汇聚区域和以透射波影响为主的区域，故本文选取10.0～14.0 m之间区域的中部12.0 m位置，即混凝土排桩后6.0 m处作为测点。

1.3 振动波波长的计算

本文以振动波波长作为混凝土排桩深度优化的参考量，多种变量下振动波波长的计算公式为

(6)

式中:λ为振动波波长(m);f为振动波频率(Hz);vr为振动波在土体中传播的速度(m/s)，其计算公式为

(7)

其中：E为土体弹性模量(Pa);ρ为土体密度(kg/m3)。

1.4 混凝土排桩深度优化方法

本文选用低频(10 Hz)作为代表进行激振，以振动波波长λ作为参考量，对混凝土排桩深度进行优化。给定土体的密度为1.8×103kg/m3，由公式(6)和(7)计算得到振动波在土体中传播的速度vr=105 m/s，振动波波长λ=10.5 m。本文采用排桩截面尺寸为1.0 m×1.0 m的方形实心混凝土桩，固定排桩间距和距路基边坡距离分别为1.0 m和5.0 m。混凝土排桩深度H设为0.1λ～1.3λ，每组有限元模型排桩深度以0.1λ递增。取桩后6.0 m处测点进行分析，其隔振效果以振动波振幅降低比Ar来表示，得到混凝土排桩隔振的地表振动波振幅降低比Ar与排桩深度H的关系曲线，见图4。

图4 混凝土排桩隔振的地表振动波振幅降低比Ar与 排桩深度H的关系曲线Fig.4 Relationship curve between the amplitude reduction ratio of ground vibration wave Ar and row pile depth H using vibration isolation of concrete row piles

由图4可见，随着排桩深度的增加，混凝土排桩的隔振效果得到明显提高，且在初期阶段提高较为快速，排桩深度由0.1λ增加到0.8λ时，其地表振动波竖向加速度衰减率可达7.95%，但排桩深度达到0.8λ后其隔振效果提升不再明显，排桩深度每增加0.1λ其地表振动波竖向加速度衰减率增加不足1%。

因此，在对混凝土排桩深度进行优化时，可以振动波波长λ为参考量，选取使排桩隔振效果得到明显提高、其后再增加排桩深度时其隔振效果提高不再明显时的极限深度作为排桩的较优深度，并以此作为隔振工程中设置排桩深度的参考。

2 不同因素下混凝土排桩的隔振效果及排桩深度优化

本文采用控制变量的方法(改变其中一个因素而其他因素保持不变)对不同因素下混凝土排桩的隔振效果及排桩深度优化进行分析研究。选取排桩截面尺寸为1.0 m×1.0 m的方形实心混凝土桩、排桩间距为1.0 m、排桩距路基边坡距离为5.0 m作为基础工况。取低频振动10 Hz进行激振，振动波在土体中传播的速度vr=105 m/s，振动波波长λ=10.5 m。混凝土排桩深度设为0.1λ～1.3λ，每组有限元模型排桩深度以0.1λ递增。

2.1 排桩距离路基边坡坡脚的距离对混凝土排桩隔振效果的影响

为了研究不同排桩距离路基边坡坡脚的距离对混凝土排桩隔振效果的影响，并对排桩深度进行优化，共采用两种方案对其进行研究：一种方案是将测点距离排桩的距离固定，而路基边坡距离排桩的距离是变化的；另一种方案为固定路基边坡到测点的距离，对应的测点到排桩的距离是变化的。通过将上述两种方案的结果进行对比，发现两者所表现的隔振规律性并无较大差异。同时，为减少绕射波和透射波等因素的影响，本文选取第一种方案进行讨论，数据采集点固定为排桩后6.0 m处测点，排桩距路基边坡坡脚的距离分别取2.0 m、5.0 m及8.0 m，排桩隔振效果以振动波振幅降低比Ar表示，得到排桩距路基边坡坡脚不同距离条件下混凝土排桩隔振的地表振动波振幅降低比Ar与排桩深度H的关系曲线，见图5。

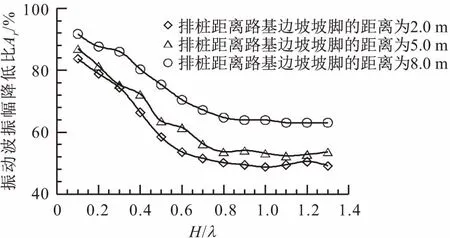
图5 排桩距路基边坡坡脚不同距离条件下混凝土排桩隔 振的地表振动波振幅降低比Ar与排桩深度H的 关系曲线Fig.5 Relationship curves between the amplitude reduction ratio of ground vibration wave Ar and row pile depth H using vibration isolation of concrete row piles in case of different distance from the row piles to the subgrade slope

由图5可见:排桩距离路基边坡坡脚不同距离情况下，振动波振幅降低比Ar所表现出来的整体趋势基本一致，且较优排桩深度均在0.8λ左右。因此，在设置排桩深度时可以不考虑其与路基边坡坡脚之间的距离。同时，在相同排桩深度下，当排桩距路基边坡坡脚距离由8.0 m变为5.0 m及由5.0 m变为2.0 m时，其地表振动竖向加速度衰减率分别提高了4.79%～11.77%及0.93%～7.83%。由此可知，减小排桩距路基边坡坡脚的距离，可明显提高排桩的隔振效果，但随着其距离路基边坡坡脚的距离越来越近，其隔振效果提升程度逐渐减弱，因此排桩隔振屏障应建立在距离路基边坡较近的位置。

2.2 排桩间距对混凝土排桩隔振效果的影响

为了研究不同排桩间距对混凝土排桩隔振效果的影响，并对排桩深度进行优化，本文采用排桩间距分别为0.5 m、1.0 m和1.5 m三种工况与无隔振屏障的工况进行了对比分析，采集排桩后6.0 m处测点的地表振动竖向加速度，排桩隔振效果以振动波振幅降低比Ar表示，得到不同排桩间距条件下混凝土排桩隔振的地表振动波振幅降低比Ar与排桩深度H的关系曲线，见图6。

图6 不同排桩间距条件下混凝土排桩隔振的地表振动 波振幅降低比Ar与排桩深度H的关系曲线Fig.6 Relationship curves between the amplitude reduction ratio of ground vibration wave Ar and row pile depth H using vibration isolation of concrete row piles in case of different distance row spacing of piles

由图6可见：在排桩间距变化的情况下，其较优排桩深度均在0.8λ左右，由此可见排桩间距的改变对排桩较优深度的影响不明显，因此在设置排桩深度时可以不考虑排桩间距的变化;在相同排桩深度下，当排桩间距由0.5 m增大至1.0 m时，其地表振动波竖向加速度衰减率提高范围在0.43%～5.19%之间；在相同排桩深度下，当排桩间距由1.0 m增大至1.5 m时，其地表振动波竖向加速度衰减率提高范围在1.29%～4.32%之间。由此可知，随着排桩间距的减小，其隔振效果总体上有提高的趋势，但是提升效果并不明显。在实际工程应用中，出于成本的考虑，可以适当增加排桩间距。

2.3 排桩截面尺寸对混凝土排桩隔振效果的影响

为了研究不同排桩截面尺寸对混凝土排桩隔振效果的影响，并对排桩深度进行优化，本文选用排桩截面尺寸分别为0.5 m×0.5 m、1.0 m×1.0 m和1.5 m×1.5 m的方形实心排桩与无隔振屏障的工况进行了对比分析，采集排桩后6.0 m处测点的地表振动波竖向加速度，隔振效果以振动波振幅降低比Ar表示，得到不同排桩截面尺寸条件下混凝土排桩隔振的地表振动波振幅降低比Ar与排桩深度H的关系曲线，见图7。

图7 不同排桩截面尺寸条件下混凝土排桩隔振的地表 振动波振幅降低比Ar与排桩深度H的关系曲线Fig.7 Relationship curves between the amplitude reduction ratio of ground vibration wave Ar and row pile depth H using vibration isolation of concrete row piles in case of different sizes of pile section

由图7可见：在不同排桩截面尺寸条件下，其较优排桩深度均在0.8λ左右，因此在设置排桩深度时可以不考虑排桩截面尺寸对较优深度的影响;当排桩截面尺寸由0.5 m×0.5 m增至1.0 m×1.0 m和由1.0 m×1.0 m增至1.5 m×1.5 m时，其地表振动波竖向加速度衰减率分别提高了3.64%～11.67%和2.32%～8.23%。由此可知，加大排桩截面尺寸可提高其隔振效果，但其提高幅度会随着排桩截面尺寸的增加而有所降低。

2.4 排桩截面形状对混凝土排桩隔振效果的影响

为了研究不同排桩截面形状对混凝土排桩隔振效果的影响，并对排桩深度进行优化，本文选用截面形状分别为方形实心、方形空心(空心率36%)和圆形实心的排桩与无隔振屏障的工况进行了对比分析，采集排桩后6.0 m处测点的地表振动波竖向加速度，隔振效果以振动波振幅降低比Ar表示，得到不同排桩截面形状条件下混凝土排桩隔振的地表振动波振幅降低比Ar与排桩深度H的关系曲线,见图8。

图8 不同排桩截面形状条件下混凝土排桩隔振的地表振 动波振幅降低比Ar与排桩深度H的关系曲线Fig.8 Relationship curves between the amplitude reduction ratio of ground vibration wave Ar and row pile depth H using vibration isolation of concrete row piles in case of different row pile shape conditions

由图8可见：在混凝土排桩截面形状分别为方形空心、方形实心和圆形实心时，其较优排桩深度分别为0.9λ、0.8λ和0.8λ，由此可见空心排桩与实心排桩相比其较优排桩深度会有所增加，但排桩截面形状的改变对其较优深度的影响不大，方形实心排桩与方形空心排桩相比，其地表振动波竖向加速度衰减率的提高幅度约为1.30%～10.39%，圆形实心排桩与方形实心排桩相比，其地表振动波竖向加速度衰减率的提高幅度约为2.43%～8.31%，可知实心排桩的隔振效果优于空心排桩，圆形截面排桩的隔振效果优于方形截面排桩。因此，在实际工程应用中，建议使用圆形实心排桩，以提高混凝土排桩的隔振效果。

3 结 论

本文以弹性半空间理论为基础，建立了采用无限元边界的有限元分析模型，以振动波波长作为参考量，通过建立振动波波长与排桩深度的关系，在多种变量下对混凝土排桩深度进行优化，并分析了不同变量对混凝土排桩隔振效果的影响，得出以下结论：

(1) 以振动波波长λ作为参考量，当混凝土排桩的排桩深度约为0.8λ～0.9λ时，混凝土排桩的隔振效果最佳。

(2) 排桩距路基边坡坡脚的距离、排桩间距、排桩截面尺寸的改变对排桩较优深度的影响均较小，空心排桩与实心排桩相比其较优深度略有增加。

(3) 减小排桩距路基边坡坡脚的距离可有效提高其隔振效果，但是随着其距离路基边坡坡脚距离的减小其隔振效果的提升程度有所降低；改变排桩间距对混凝土排桩隔振效果的影响不明显；增大排桩截面尺寸可以提高混凝土排桩的隔振效果，但是其隔振效果提升程度会随着排桩截面尺寸的增加而有所降低；实心排桩的隔振效果优于空心排桩，圆形截面排桩的隔振效果优于方形截面排桩。