特高压直流输电线路塔基边坡的稳定性分析
2019-12-05谢寿平刘志鹏罗红明王大庆苏云鹏
谢寿平,刘志鹏,罗红明,王大庆,杨 桦,刘 凯,苏云鹏
(1.贵州高速公路集团有限公司,贵州 贵阳 550004;2.中交第二公路勘察设计研究院有限公司,湖北武汉 430056;3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,湖北 武汉 430071)
输电线路横跨不同的地貌地质单元,山区输电线路工程塔基一般修建于自然斜坡上,一方面斜坡自身的稳定性会影响到塔基的安全,另一方面输电线塔具有结构高、跨度大等特点,铁塔荷载与风荷载等塔基荷载会直接作用于斜坡坡顶,对斜坡的稳定性有较大的影响,从而威胁输电线路工程的安全。因此,塔基的稳定性状况是影响输电路线工程安全的关键技术难题。
目前,对于斜坡地基承载力方面的研究,已取得了较为丰硕的成果[1-2]。关于塔基边坡稳定性方面的研究也较多,如赵健等[3]采用3DEC离散元方法对边坡开挖并截断锚索和边坡新增支护并新建铁塔两种工况下的边坡稳定性进行了分析;胡江运等[4]采用三维数值模拟方法分析了跨越塔基边坡的稳定性。但这些研究成果仅仅只关注将铁塔荷载作用在边坡上,重在分析铁塔荷载对边坡稳定性的影响。近年来国内外对斜坡桩基承载力分析方面的研究也颇多[5-11],重在分析斜坡对桩基承载力的影响,则很少关注边坡稳定性对塔基承载力的影响以及边坡与塔基间的相互作用问题。鉴于此,本文以修建于自然斜坡上的甘肃酒泉—湖南±800 kV特高压直流输电工程5535#塔基边坡为例,采用三维有限差分数值模拟方法,利用FLAC3D软件系统研究了该塔基和塔基边坡的稳定性,评价塔基边坡在工程活动影响下的稳定性,对保证塔基边坡的长期稳定具有重要的工程意义。
1 塔基边坡概况
1.1 塔基边坡概况
甘肃酒泉—湖南±800 kV 特高压直流输电线路工程5535#铁塔塔型为JC30152C-45,转角度数为左转0°37′,该铁塔塔位位于长江边低山地貌的山脊坡,塔址处原为柏树林,前坡坡向为220°、坡度为15°~20°,左坡坡向为140°、坡度为37°~43°(铁塔B腿桩中心15 m以外边坡坡度变为45°~60°),右坡坡向为310°、坡度为35°~42°(铁塔D腿桩中心5.7 m以外边坡坡度变为43°~46°,35 m以外边坡坡度变为50°~60°),局部地段白云质灰岩出露,岩层产状为347°∠18°,见图1。
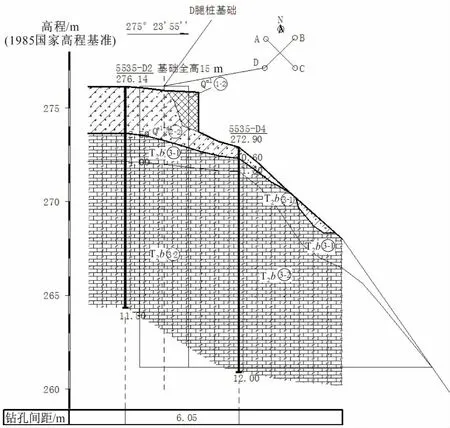
图1 甘肃酒泉—湖南±800 kV特高压线路工程5535# 塔基边坡工程地质剖面图Fig.1 Engineering geological profile of 5535# tower foundation slope of Jiuquan-Hunan ±800 kV UHV DC transmission line
1.2 工程地质概况
根据钻探揭露和区域地质资料,5535#铁塔塔位的地层岩性在钻探所达深度范围内分为含碎石粉质黏土层和白云质灰岩,各地层的地质特征如下:
白云质灰岩(T2b):浅灰色、灰白色,中等风化,隐晶质结构,中厚层状构造,节理裂隙发育,其中岩体较破碎段埋深为2.5~4.0 m,岩体较完整段埋深为4.0~20.0 m。
根据现场调查和钻探资料,5535#塔基区表层为第四系覆盖层,其下基岩为白云质灰岩,第四系覆盖层最大厚度为2.5 m,位于边坡坡顶平缓位置,而边坡中下部坡面基岩直接裸露于地表,未见有任何的变形破坏迹象,说明该边坡的稳定性较好。
2 塔基边坡稳定性分析模型的建立
2.1 分析方法
塔基边坡的稳定性分析采用工程实践中应用广泛的三维有限差分数值模拟方法,该方法采用显式有限差分格式来求解场的控制微分方程[12],并应用混合单元离散模型,准确地模拟材料的屈服、塑性流动、软化直至大变形,在材料的弹塑性分析、大变形分析以及模拟施工过程等方面有其独到的优势[13]。
2.2 计算模型
从5535#铁塔的A、B、C、D腿桩平面位置来看,D腿桩离边坡最近,故选取D腿桩来进行塔基稳定性分析。根据工程经验,铁塔D腿桩在水平荷载作用的影响范围约为桩径的3~4倍,桩端影响深度约为桩径的2~4倍。三维数值计算模型最大尺寸取为36 m×30 m×10 m,以减小模型边界效应的影响[14],三维数值计算模型采用六面体网格剖分,共剖分了8 170个单元,9 658个节点。本文建立的三维数值计算模型与网格剖分,见图2。
计算模型的左右、前后和底部边界均采用约束边界,其中左右边界施加x方向位移约束,前后边界施加z方向位移约束,底部边界施加y方向约束。
2.3 本构模型和计算参数
5535#铁塔的塔基边坡岩土体变形破坏采用摩尔-库仑弹塑性模型进行计算,该模型的破坏包络线对应于摩尔-库仑判据(剪切屈服函数)加上拉伸分离点(拉伸屈服函数),与拉应力法则相关联而与剪切流动不相关联。5535#铁塔的D腿桩基采用FLAC3D程序自带的pile结构单元,它通过耦合弹簧来实现D腿桩基受垂直荷载和水平荷载作用下桩与边坡之间的相互作用[15]。
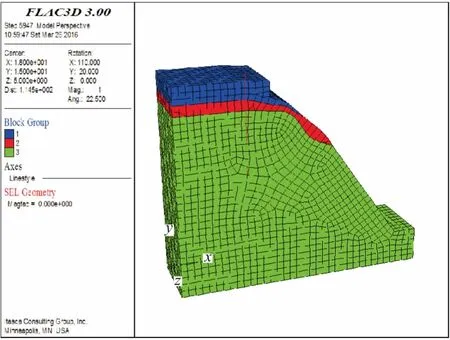
图2 三维数值计算模型与网格剖分Fig.2 Three-dimensional numerical computational model and meshing
根据地质勘察资料,结合现场实际情况,岩土体和桩采用的计算参数见表1和表2。

表1 岩土体的计算参数Table 1 Calculation parameters of rock and soil mass

表2 桩的计算参数Table 2 Calculation parameters of pile
2.4 计算工况
本模型计算仅考虑重力场作用和D腿桩基受抗压、抗拔与水平荷载共同作用下的塔基边坡稳定性和塔基稳定性。作用于铁塔基础上的水平荷载和垂直荷载是根据铁塔可能受到荷载进行计算分析得到的,由结构设计提供的最不利工况的垂直荷载和水平荷载。模拟计算工况如下:
工况1:自然边坡初始状态模拟;
工况2:建立pile单元,在桩顶施加垂直荷载3 872 kN,并施加坡外的水平荷载1 066 kN,见图3。

图3 塔基桩结构及桩顶荷载Fig.3 Pile structure and pile top load of the tower foundation
作用于5535#铁塔基础上的垂直荷载和水平荷载是根据该铁塔可能受到的荷载进行计算分析得到的,上述荷载是设计提供的最不利工况下的垂直荷载和水平荷载。
3 塔基和塔基边坡的稳定性分析
3.1 塔基的稳定性分析
为了分析塔基的稳定性,利用FLAD3D软件模拟得到塔基桩在垂直荷载和水平荷载共同作用下的受力变形结果见图4,塔基桩单元节点和桩周岩土层单元节点的水平位移见图5。

图4 塔基桩在垂直荷载和水平荷载共同作用下的受力 变形模拟结果Fig.4 Deformation of pile under tower load vertically and horizontally

图5 塔基桩和桩周岩土层单元节点的水平位移Fig.5 Horizontal displacement of nodes in pile and surrounding rock
由图4和图5可见,塔基在荷载作用下,桩顶位置产生了向坡外向下的位移,桩端位置产生了向坡内的位移,且坡顶位置水平位移最大,总位移值约为4.234 mm,其中桩水平位移最大值为4.025 mm,处于桩水平变形允许范围内;在离桩顶超过10 m后,桩的水平位移指向坡内,且变形量小于1 mm;桩周岩土层单元节点的水平位移指向坡外,且最大水平位移值为3.597 mm,在白云质灰岩(较完整)岩层中,岩土层单元节点的水平位移均小于0.7 mm,在离桩顶超过10 m后,岩土层单元节点的水平位移指向坡内,且其水平位移均小于0.3 mm。
3.2 塔基边坡的稳定性分析
为了分析塔基边坡的稳定性,利用FLAD3D软件模拟得到两种工况下塔基边坡桩中心位置x方向的应力等值线图、塔基荷载作用下塔基边坡的位移矢量图、塔基边坡的破坏分布图,见图6、图7和图8。

图6 两种工况下塔基边坡桩中心位置x方向的 应力等值线图Fig.6 x-direction stress contour map at the pile center of the tower foundation slope in two working conditions
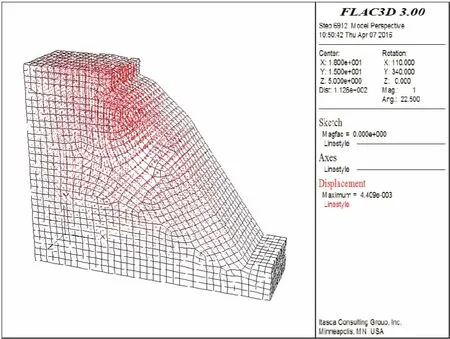
图7 塔基荷载作用下塔基边坡的位移矢量图Fig.7 Displacement vector of the tower foundation slope under tower load
由图6可见,塔基荷载作用对边坡初始应力场的影响不明显,绝大部分垂直荷载和水平荷载由桩基自身承担,仅在桩周附近单元的应力发生了变化,离桩位置较远部位单元的应力没有受到影响,尤其是在桩顶位置及桩上部向坡内侧单元出现了拉应力,而在桩上部向坡外侧单元及桩端压应力相比自然状态有了较大程度的增加。
由图7可见,在塔基荷载作用下坡顶位置产生向坡外向下的位移,总位移量较小,仅为4.409 mm。

图8 塔基边坡破坏区分布图Fig.8 Damage zone distribution map of of the tower foundation slope
由图8可见,边坡受塔基作用下应力荷载作用后,仅在坡顶产生了拉破坏单元,边坡下部陡峭部位没有产生破坏单元,表明塔基附近的坡顶出现了局部破坏,坡顶以下坡体处于弹性变形范围,未形成整体变形失稳的破坏区,预示着宏观上将表现为地表产生微裂隙,但不影响边坡整体的稳定性。因此,在塔基荷载作用下该边坡处于稳定状态。
本文提取距离塔基位置4 m坡顶处x方向上的初始应力和塔基荷载作用下的应力进行了对比,其结果见图9。

图9 塔基边坡坡顶处x方向上的初始应力和塔基 荷载作用下的应力对比Fig.9 Comparison of the inital stress and the stree at the top of tower foundation slope under tower foundation load in the x direction
由图9可见,在塔基荷载作用下,距离坡顶0~3 m范围内的应力变化很小,距离坡顶4~9 m范围内的应力有所增加,9 m深度以下的应力几乎无变化。由此可见,塔基荷载作用只是改变了坡体局部应力,且应力影响范围也较小,不会影响到塔基边坡的稳定性。
4 结 论
采用三维有限差分数值模拟方法,利用FLAD3D软件对酒泉—湖南±800 kV特高压直流输电线路工程5535#铁塔塔基边坡的稳定性进行系统分析,得到如下结论:
(1) 塔基在荷载作用下,桩顶位置产生了向坡外向下的位移,桩端位置产生了向坡内的位移,且坡顶总位移值约为4.234 mm,其中桩水平位移最大值为4.025 mm,均在桩水平变形允许范围内,表明塔基荷载主要由桩基承担。
(2) 在塔基荷载作用下,边坡坡顶位置局部范围内应力有所变化,其他范围内的应力几乎无变化,塔基荷载对边坡应力的影响范围较小,不会影响到边坡的稳定性。
(3) 在塔基荷载作用下,仅在边坡坡顶局部出现拉破坏,坡顶以下其他坡体处于弹性变形范围,未形成整体变形失稳的破坏区,对边坡的整体稳定性影响甚微。
(4) 建议对塔基边坡坡顶进行适当的加固处理,以满足特高压直流输电线路工程安全运行的要求。
