耦合溃口演变的二维洪水演进数值模型研究
2019-12-05马利平侯精明张大伟夏军强李丙尧宁利中
马利平,侯精明,张大伟,夏军强,李丙尧,宁利中
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2.中国水利水电科学研究院,北京 100038;3.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
我国是世界上修建水库最多的国家,小型水库约占我国已建水库总数的95%以上,其中94.8%的坝型为土石坝。1998年以后,由于国家和地方加大了对病险水库的除险加固工作,近期年平均溃坝率为9.3×10-5,已处于较低水平[1]。但是,每年仍有因极端事件而引起的溃坝事故发生。此外,近年来山体滑坡造成的堰塞湖事故多有发生,如2018年金沙江白格堰塞湖和雅鲁藏布江米林堰塞湖,这些堰塞湖均对下游造成了严重危害。为减少此类灾害造成的生命财产损失,采用数学模型对溃坝事故进行模拟以确定风险范围,为应急决策者提供决策依据就显得尤为重要。
在溃坝水流模拟研究中,溃口流量的计算与溃坝洪水演进的模拟是研究溃坝问题的重点。目前,计算溃口流量的数值模型已有很多。如Fread[2]于1984年开发的DAMBRK模型,该模型被用于美国国家气象局的溃坝洪水预报工作;Singh等[3]开发的BEED模型,该模型曾应用于4起历史溃坝事故,模拟结果中溃坝洪峰流量和溃口形成时间都与观测值拟合良好,但溃口顶部的计算值与观测值偏差较大;Fread[4]于1988年提出的BREACH模型,该模型可模拟由漫顶和管涌引起的溃坝,曾应用三起溃坝实验进行了检验,模拟结果与观测值拥有较好的一致性,但在洪峰流量上有一定的偏差。Wu[5]于2013年提出的溃坝模型,该模型可模拟漫顶和管涌引起的溃坝,并应用物理实验和实际案例的50组数据进行了验证,在溃口峰值流量、溃口宽度上都与观测值基本吻合;在洪水演进方面,河道的一维模型由于其较高的计算效率和灵活性而得到广泛应用[6],如张大伟等[7]基于地理信息系统开发的一维溃坝洪水分析系统,可快速、便捷地对溃坝洪水风险进行分析计算,但溃坝洪水通常会冲入下游平原地带,此时水流具有明显的二维运动性质,一维模型便不再适用。为此夏军强等[8]在无结构网格下建立了采用有限体积法的二维水动力模型,模拟研究了溃坝洪水在复杂边界及实际地形上的流动过程。曹引等[9]基于结构网格建立了适应复杂地形和不规则边界的二维水动力模型,并通过物理实验和实际算例对模型进行了验证。但溃坝过程是一个包含上游库区水动力、溃口演变和下游淹没区洪水演进的过程,以上学者均未完全考虑此过程,胡晓张等[10]建立了包含该过程的数学模型,其在上游库区采用一维模型,下游淹没区采用二维水动力模型,溃口采用宽顶堰公式进行连接,但该模型溃口过程较为简单,未考虑溃口演变的土动力学问题。同时,溃坝洪水的二维演进过程普遍距离长、范围大,从而导致计算量极大,为提高计算效率,许栋等[11]通过基于信息传递接口(MPI)的集群计算技术实现大范围洪水演进模拟,但该方法需在大型并行计算集群上运行,所需成本较高。
本文采用源项法将溃口演变模型DB-IWHR和基于GPU加速技术的二维水动力模型进行耦合,建立了一个包含上游库区二维水动力过程、溃口演变和下游淹没区二维洪水演进的高性能全过程耦合模型。通过对一个土石坝和两个堰塞坝溃决算例的模拟,耦合模型对上游库区、溃口流量、下游演进区的模拟效果较好,且计算效率较高,验证了耦合模型的可靠性和适用性。
2 模型简介
耦合模型使用源项法将溃口演变模型(DB-IWHR)与基于GPU加速技术的二维水动力模型耦合起来,可实现对土石坝、堰塞坝溃坝流量的计算及上游库区水动力与下游洪水演进过程的高性能模拟。
2.1 溃口演变模型本文采用的溃口演变模型为Chen等[12]提出的DB-IWHR溃坝模型,该模型主要包括溃口流量计算、溃口冲刷和溃口扩展三部分。
溃口流量采用宽顶堰公式进行计算,公式如下:

式中:Q溃口流量,m3/s;C为流量系数,建议的取值范围为1.43~1.69m1/2/s[13];B为溃口宽度,m;H为水库水位,m;zb为溃口底高程,m。在溃口演变计算中,溃口扩展过程通过B反映,溃口冲刷过程通过zb反映,两者的变化共同模拟溃口演变过程。
溃口冲刷过程为Chen等提出的双曲线模型[12],其表达式为:

式中:v=k(τ-τc)为扣除临界剪应力后的剪应力,k为在剪应力τ范围内允许dz/dt接近其极值的单位变换因子,τc为临界剪应力,此处k取100[13]。双曲线模型有一当v接近无限值时的渐近线(见图1),其值为1/b,它代表了土体可能的最大侵蚀率;1/a表示v等于0时曲线的斜率。其中τ可由下式计算:

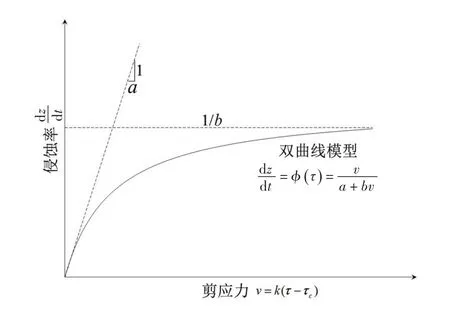
图1 双曲线侵蚀率模型
式中:γ为水的容重,N/m3;J为引流槽坡降;R为水力半径,m,若渠道宽度B远大于水深h,R可近似取h;n为糙率。
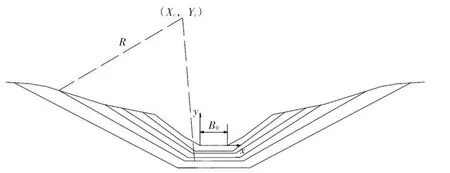
图2 溃口侧向崩塌过程等效简化图
溃口扩展过程为岩土工程中已经被广泛使用的圆弧滑动面总应力分析方法:简化的Bishop法。通过搜索可能的滑裂面,进行溃口扩展的数值模拟,在实际计算过程中,溃口的模拟崩塌过程可简化为图2的梯形断面崩塌[14]。假定横向扩展等于下切深度,对整个溃口断面而言,两侧均向河岸靠近,则有:

式中:Bend为溃口终止宽度;B0为溃口初始宽度;z0为溃口初始底高程;zend为最后一个滑面的渠底高程,即溃口停止扩展时的溃口底高程。
取水面宽度为溃口宽度,水面宽度B为:
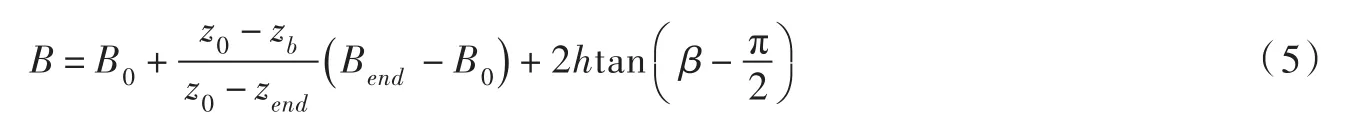
式中:h为溃口处水深,由于在此处该值未知,可采用上一步的h进行计算;β为溃口边坡与溃口底部之间的夹角,可用下式计算β:

式中:β0为溃口边坡与溃口底部之间的初始夹角,可假定边坡处于自然休止角来确定β0;βend为在最后一个滑面时,溃口边坡与溃口底部之间夹角。
2.2 二维水动力模型
2.2.1 控制方程 本文应用二维浅水方程来模拟溃坝洪水的演进过程,其矢量形式[15]如下:
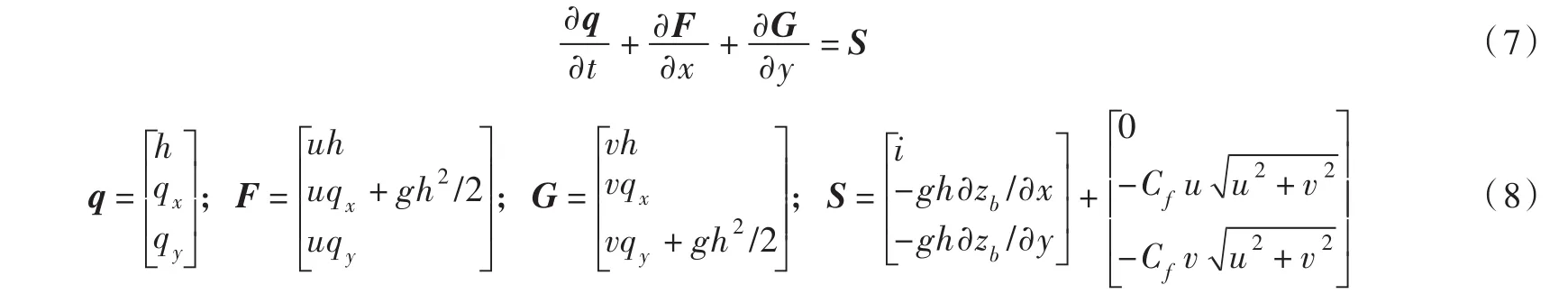
式中:q为变量矢量,包括水深h、两个方向的单宽流量qx和qy;g为重力加速度;u和v分别为x、y方向的流速;F和G分别为x、y方向的通量矢量;S为源项矢量;zb为河床底高程,为床面摩擦系数,n为曼宁系数。
2.2.2 数值方法 本模型采用Godunov格式的有限体积法求解二维浅水方程。网格单元界面通量应用HLLC格式的近似黎曼求解器求解[16]。通过静水重构来修正干湿边界处负水深。底坡源项使用模型作者提出的底坡通量法处理。摩阻源项的计算使用半隐式法来提高稳定性[17]。采用二阶显式Runge Kutta[18]法进行时间步长的推进。从而构造具有二阶时空精度的MUSCL型格式,有效解决复杂地形干湿界面处的负水深和伪高流速等现实中不存在的物理现象所造成的计算失稳和物质动量的不守恒。因溃坝洪水演进过程模拟一般尺度较大,为提高计算效率,模型作者通过CUDA语言自主编程实现GPU并行计算技术,以达到高速运算的目的[19]。
2.3 模型构建耦合模型采用基于水量平衡的源项法将一维溃口演变模型(DB-IWHR)与二维水动力模型进行耦合连接。其中溃口演变模型用来计算溃口流量过程,该模型最大的优势是在模拟溃口冲刷时采用陈祖煜等提出的双曲线冲刷模型[12],该冲刷模型在溃口冲刷的计算中比线性模型、指数模型更稳定,并且在实际工程应用中可帮助有经验的工程师减少采用不正确的侵蚀参数而造成的风险;二维水动力模型用来模拟溃口上下游区域的水动力过程,该模型由Hou[18-19]等开发,在解决复杂地形干湿界面时更加稳定,且采用GPU并行技术进行加速计算。
二维浅水方程的源项(式(7)中S)包括底坡源项、摩阻源项及耦合溃口流量的源项(式(8)中i),通过耦合溃口流量的源项i将溃口演变模型计算的流量转换为二维水动力模型溃口上下游各标记网格单元水深的变化值,以此来实现溃口上下游之间的水量交互,即为源项法。该方法简单易实现,且具有良好的网格适应性,不需特殊处理计算网格通量的HLLC黎曼求解器。图3为源项法耦合示意图,图中红色网格为土石坝区域,土石坝区域的网格仅用来描述建筑物的体型,红色网格之外的二维计算区域Ⅰ为上游库区,二维计算区域Ⅱ为下游洪水演进区。编号为2的网格为上游溃口处入流网格,编号为3的网格为下游溃口处出流网格,两种网格个数相同,网格选取的位置及个数依据溃口位置及溃口最大宽度而定,上下游的水量交互便是通过这些特殊网格实现,而溃口的扩展过程仅体现在耦合模型的一维溃坝部分中,二维水动力部分的这些特殊网格是固定的,不体现溃口扩展过程。
将溃口演变模型通过式(1)计算的溃口流量Q平均分配到上游溃口各网格,经式(9)计算后得到上游溃口处各网格单元同一时间步长内水深的变化值,对于上游溃口网格,各网格水位减去水深变化值,即为下一时刻水位值?(式(10));对于下游溃口网格,各网格水位?加上水深变化值,即为下一时刻水位值(式(11))。

式中:Q为溃口流量,m3/s;l为网格单元长度,m;w为网格单元宽度,m;Nc为上游溃口处网格单元个数;dt为模拟时间步长,s;dh为同一时间步长内单个网格单元水深的变化值,m。



图3 耦合方法示意图
2.4 GPU加速技术图形处理器(GPU)作为图形渲染设备,由于其拥有成百上千个算术运算核且内存访问带宽是同期CPU的5~10倍[20],因此GPU非常适合执行并行计算任务。模型作者通过CUDA语言,将求解二维浅水方程的各项运行于GPU上,实现了在空间上大规模计算各网格水力要素信息;采用C++语言,将数据的读写、变量初始化运行于主机CPU上,实现了模型的设置。图4为耦合模型框架图,主要描述了耦合模型计算溃坝洪水时所需的输入数据、主机与显卡GPU之间的数据交换、源项法的主要步骤及在GPU上求解浅水方程各项的计算流程。
3 工程算例
选取西班牙托斯大坝溃坝、唐家山堰塞湖溃坝、金沙江白格堰塞湖溃坝作为本文的研究案例。这3个案例均属于本文所研究的漫顶逐渐溃坝。而漫顶逐渐溃坝又包含土石坝溃坝和堰塞坝溃坝,这两类溃坝也正是目前我国主要的两种溃坝类型。其中西班牙托斯大坝为黏土心墙土石坝,这类大坝在我国是应用最广泛的坝型;唐家山堰塞湖溃坝和金沙江白格堰塞湖溃坝为山体滑坡后松散的堆积体堆积形成的堰塞坝溃坝,近年来,我国由于山体滑坡造成的堰塞湖事故明显增多,仅2018年,在金沙江和雅鲁藏布江便发生了4起由山体滑坡导致的堰塞坝溃坝事故。

图4 耦合模型原理图
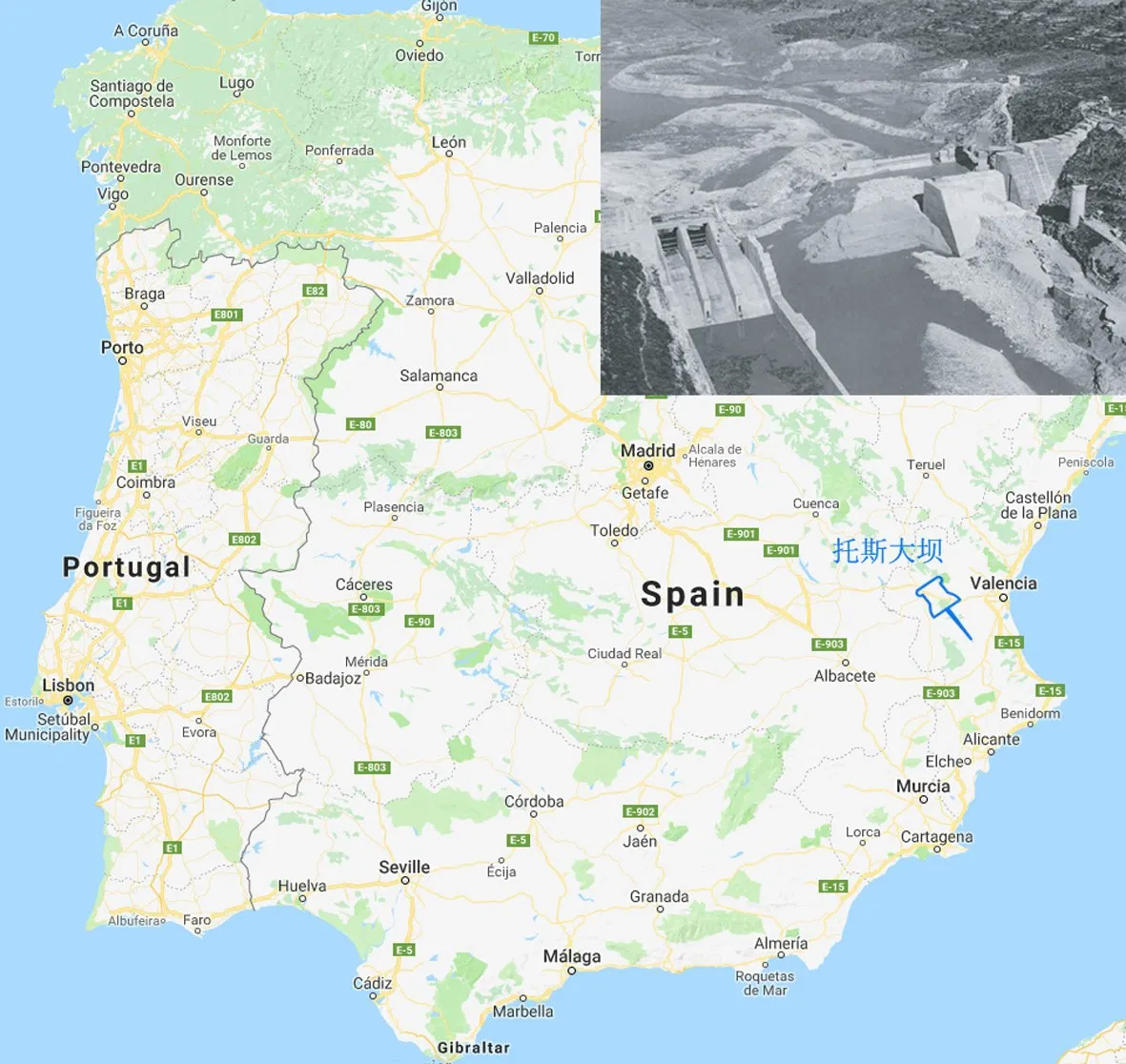
图5 托斯大坝位置图
3.1 托斯大坝溃坝托斯大坝位于西班牙胡卡尔河流域,其集水面积达到17820 km2(图5)。1982年10月20日至21日,胡卡尔河流域发生了一场极端暴雨,巨大的洪水汇流直下,直接导致下游的托斯大坝溃坝[21]。由于托斯大坝溃坝后当地政府以及很多洪水研究机构都对此次事故进行了调研,得到了该溃坝事故的详细数据资料,因此本文也应用此算例进行溃口流量及洪水演进数学模型的计算验证。
3.1.1 模型设置 根据托斯大坝溃坝后当地调研机构的数据,大坝溃坝期间水位并未超过98.5 m,故给予初始水位98.5 m。初始溃口底高程为96.0 m,初始溃口宽度取40 m。由于在大坝溃坝期间,仍有源源不断的水从上游流域汇聚而来,根据CEDEX(西班牙公共工程部研究和实验中心)提供的数据,当时汇入托斯水库的流量过程线如图6所示,将此流量过程线作为入库流量输入到溃口演变模型中。溃口流量计算参数见表1。

表1 托斯大坝溃口演变模型计算参数
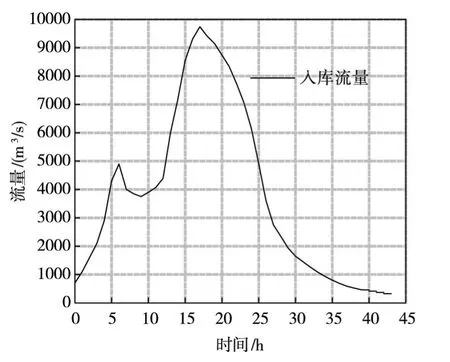
图6 托斯大坝溃坝期间入库洪水过程线
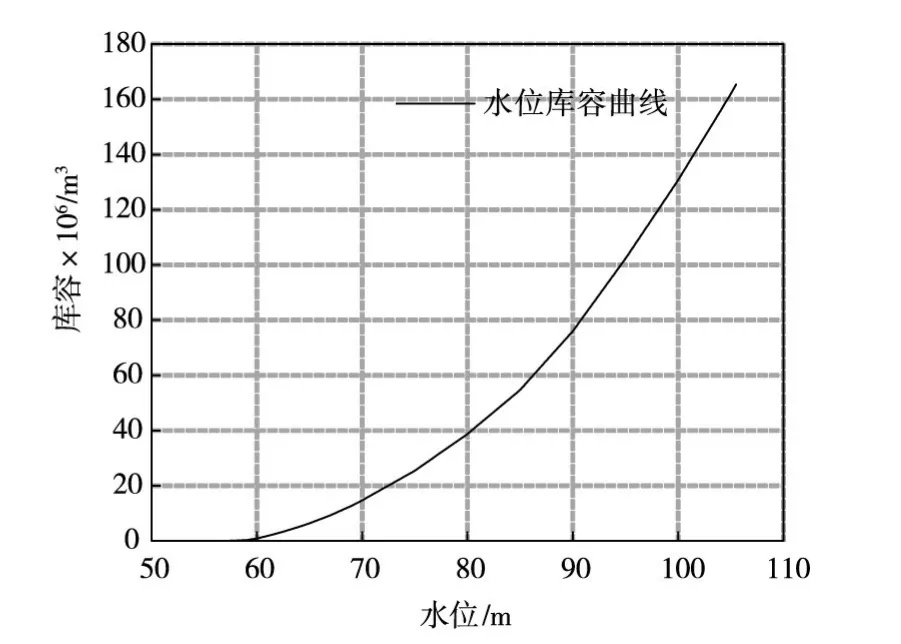
图7 托斯大坝水位库容曲线
本文模拟采用的数字地形高程数据由CEDEX提供(图8),网格精度为8 m,共有163 830个网格单元。在溃口处,由于在未发生溃坝之前存在一段时间的溢洪道过流,故将溢洪道过流流量与模拟溃坝流量拼接起来共同作为入流数据(图12),并采用源项法将其耦合进去,实现大坝下游的入流,入流位置为图8中红线,共模拟38 h,下游边界为自由出流边界,其余为闭边界。由于在测量点1两侧分布有大片橙园(图9中橙色位置),根据Alcrudo和Mulet[21]提供的曼宁系数参考值,选取河道曼宁系数0.04,橙园曼宁系数0.09。本次模拟验证,主要模拟大坝下游7 km的洪水演进过程,并在下游5.7 km处(测量点1),将耦合模型计算的水深与实测数据进行了比较。
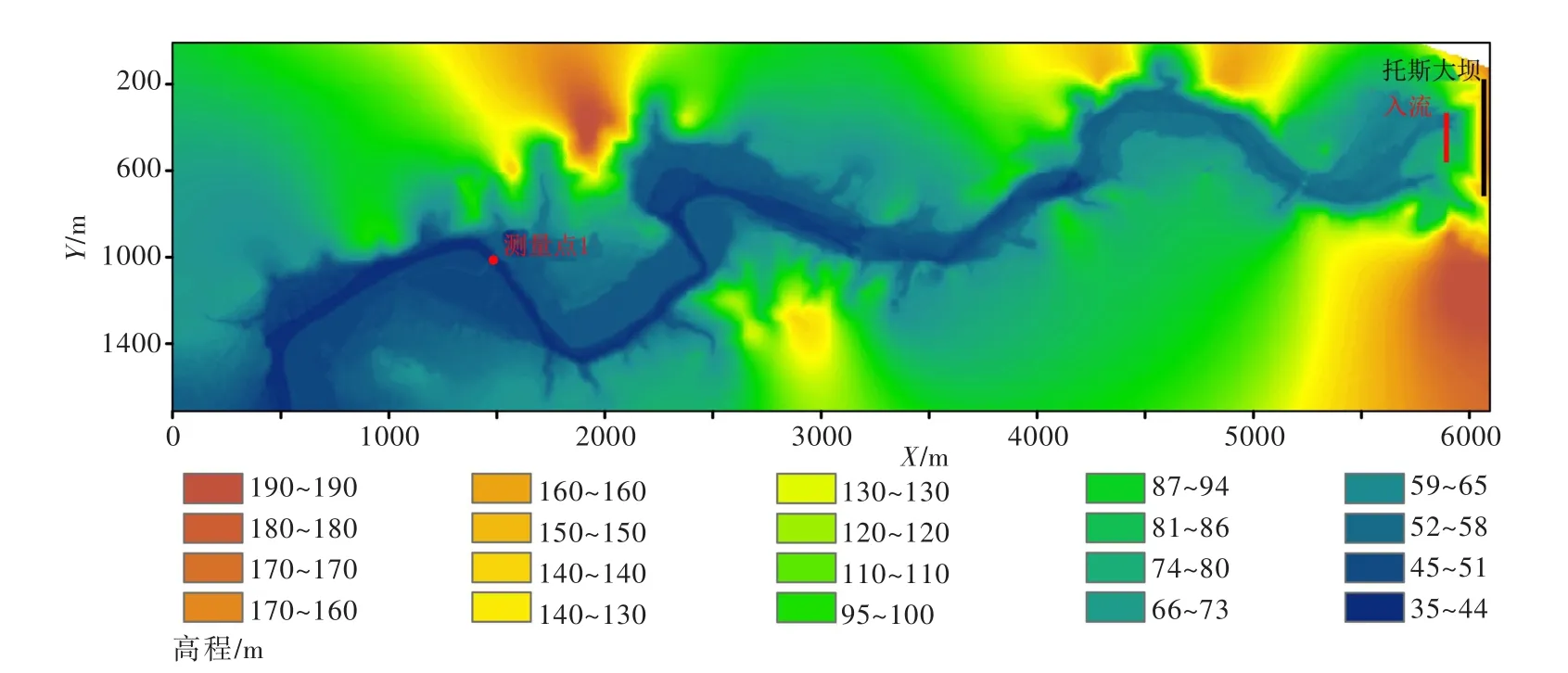
图8 研究区域地形图(相对坐标)

图9 测量点1处橙园分布图
3.1.2 结果分析 根据Alcrudo和Mulet的论文[21],在大坝失事期间,溢洪道闸门处于关闭状态,由CEDEX提供的闸门关闭情况下溢洪道水位流量曲线(图10)可知,在库水位达到98.5 m时,溢洪道流量为3252 m3/s,在此之后大坝开始溃决。由图11实测溃坝流量过程线可知,在流量达到3252 m3/s时,对应的时间为第11 h,故从第11 h开始,大坝开始漫顶。从实测溃坝流量过程线分析,漫顶后并未立即发生溃坝,而是经过1 h后溃坝才开始,因此将溃口演变模型计算的溃坝流量过程线的起点放于第12 h处。
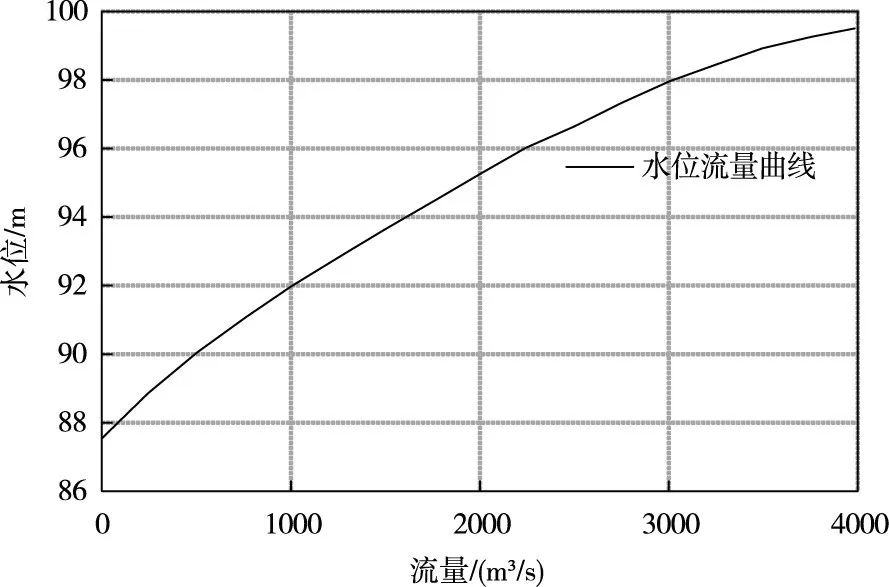
图10 溢洪道关闭闸门情况下水位流量曲线

图11 托斯大坝溃口处实测与模拟洪水过程线
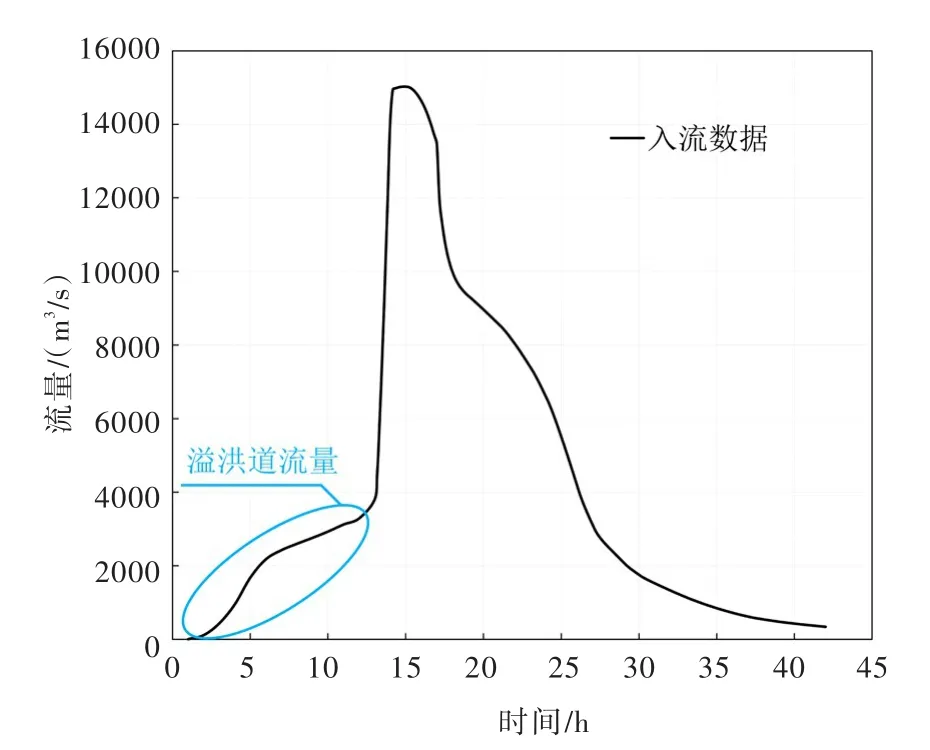
图12 入流数据(溢洪道流量与模拟流量拼接后)
在测量点1处有两种不同来源的实测数据,由于实测数据2的洪峰峰值比实测数据1的洪峰峰值高,属于最危险的情况,故本文采用数据2与模拟结果进行对比。通过测量点1处的水深对比图(图13)可以看出,在大坝未漫顶之前,对于仅从溢洪道过流水流的下游演进模拟,耦合模型模拟的结果与实测数据吻合很好,说明耦合模型计算的洪水到达时间及到达时的流量很准确。从溃坝起始时刻开始(第12 h),测量点1处的水深快速上升,2 h后水深达到最大,最大水深为18.41 m,与实测最大水深相比,模拟最大水深延迟21 min,减小0.58 m。在水深下降阶段,模拟水深与已有的一个实测数据相比,水深减少了0.68 m,模拟结果较好。采用模拟值与实测值的均方根误差RMSE来评价模型的可靠度。RMSE是评价误差效果的常用指标,值为0表示完全吻合,如果该值小于实测值标准偏差的一半,则表明模型性能良好[22]。RMSE公式为:

式中:Mi为第i个模拟值;Si为第i个实测值;N为模拟值或实测值数据总个数。经计算模拟结果的RMSE为0.4045,实测值的标准偏差为3.3367,RMSE小于实测值标准偏差的一半,模型性能良好。

图13 测量点1处水深模拟与实测结果图
3.1.3 耦合模型与MIKE21 FM模型对比分析 耦合模型的水动力模块与MIKE21 FM模型的水动力模块均通过有限体积法求解二维浅水方程,关于两个模型之间的数值方法,文献[23]做了详细的叙述,本文不再赘述。应用耦合模型与MIKE21 FM模型分别模拟托斯大坝溃坝算例,两个模型在参数选取及模型设置方面基本保持一致。不同的是耦合模型采用的入流方式为文中使用的源项耦合法,而MIKE21 FM模型采用的入流方式为边界流量入流。两者的区别在于前者仅考虑水量守恒,未考虑溃口入流处水流速度,而后者考虑了速度,但这一不同仅影响溃口近区的水流流态,且影响很小。
耦合模型与MIKE21 FM模型计算的测量点1处的水深对比结果见图14,在溢洪道过流演进阶段,MIKE21 FM计算的水深比实测小1 m左右;在溃坝发生后的过流演进阶段,其水深过程出现略微的延后现象;在退水阶段,水深与实测数据吻合很差且水深过程出现震荡现象。这是由于MIKE21 FM在干湿水深设置时为了提高模型的稳定性而采用“高级干湿水深”选项来计算,从而降低了模型计算的精度,图15为MIKE21 FM模拟的水面高程图,从图中红色方框区域可以看出在模型模拟过程中出现了现实中不存在的非正常现象。而耦合模型在溢洪道过流演进阶段及溃坝发生后的过流演进阶段的模拟水深结果均与实测吻合很好,在退水阶段也与实测较为接近。在计算效率方面,耦合模型和MIKE21 FM模型均采用GPU加速技术,所用硬件为英伟达RTX 2080显卡。耦合模型模拟耗时3722s,MIKE21 FM模型耗时63 450 s,耦合模型的计算效率是MIKE21 FM的17.04倍。
3.2 唐家山堰塞湖溃坝洪水模拟

图14 耦合模型与MIKE21 FM模型模拟与实测水深对比图
3.2.1 研究区域概况及计算条件的确定 2008年5月12日,四川省西南处的汶川县发生8.0级地震,该地震造成唐家山处山体滑坡,从而堵塞河道形成堰塞湖。本文以堰塞坝至上游20 km,至下游33.5 km长的河段为研究对象,模拟研究溃口流量过程及上下游的水动力过程。由于该区域精细地形难以获取,故基于美国对地观测卫星Terra提供的30 m分辨率DEM地形数据(图16),利用遥感影像划定河道轮廓,依据曼宁公式计算河道最大正常水深,以最大正常水深作为下挖深度来概化出水下河道地形。研究区域模拟网格总数35万。堰塞坝溃坝流量计算参数见表2,结果见图17。在堰塞坝溃口处,采用源项法将溃坝流量耦合进去,实现上下游的连接,下游边界为自由出流边界,上游边界为入流边界,入流数据为实测入库流量80 m3/s,其余边界为闭边界。根据之前学者对唐家山堰塞湖下游洪水演进的模拟经验,曼宁系数取0.035[24],共模拟24 h。

图16 研究区域地形图(相对坐标)
3.2.2 模拟结果分析 图18为堰塞坝溃决过程中上下游不同时刻的水深图,可以明显地看到下游洪水演进、上游库区水位下降、淹没范围逐渐减小的过程。图19为t=5h堰塞坝上下游局部速度矢量图,图中箭头长度代表速度大小,箭头方向代表速度方向。从图中可看出上游库区的速度普遍很小,只在溃口近区速度逐渐变大;在下游河道区域,速度在接近180°的弯道处出现明显的衰减,意味着能量的损失,这与实际现象是一致的。选取下游北川与通口处的实测流量过程与耦合模型模拟结果对比,其中下游北川距堰塞坝7 km,通口距堰塞坝33.5 km,模拟耗时18 min。从模拟结果图20可看出,北川处模拟与实测吻合较好,通口处的流量过程在上升阶段略有延迟。在北川处洪水到达时间延迟15 min,但随后流量上升速度加快,洪峰流量比实测小167 m3/s(2.55%),峰现时间一致,产生误差的主要原因是在溃坝初期(8:00—10:00),模拟的溃坝流量过程比实测溃坝流量过程小,从而导致了在北川处流量上升过程产生延迟;在通口处,溃坝洪水流量过程在上升阶段整体延后60 min左右,洪峰流量比实测小64 m3/s(1.07%),产生误差的主要原因是当洪水流经堰塞坝下游14.5 km至19 km河段时(地形图中红框区域),因已有低分辨率地形资料不能反映实际河槽形态,断面较实际呈宽浅,计算洪水出现了漫滩演进现象,致使洪水在滩地铺展开,受到的摩擦阻力增大,从而使得溃坝洪水流量过程在上升阶段出现延迟。从不同时刻水深图可看出,洪水演进的过程中,红框区域的水深相对其上下游水深均比较浅,也进一步证实了这一点。
3.3 “11.03”金沙江白格堰塞湖溃坝洪水模拟
3.3.1 研究区域概况及计算条件的确定 金沙江白格堰塞湖位于西藏自治区昌都市江达县和四川省甘孜藏族自治州白玉县交界处,2018年10月10日与11月3日,位于金沙江右岸西藏江达境内的山体在同一位置分别发生滑坡。由于二次滑坡的土石方堵塞了初次滑坡后自然泄流冲出的水槽[25],同时在初次滑坡的土石方上再堆积,致使堰塞坝高度升高,危险增加。故本文以发生在“11.03”的第二次堰塞湖事故为模拟研究对象。
由于研究区域的高精度地形资料难以获取,故同样采用本文3.2节所用方法获取DEM数据(图21)。在概化河道时,首先根据同时期卫星影像地图,在DEM上将河道平面轮廓划定出来,由于采用同时期卫星影像地图,故河道水面轮廓不会发生较大的变化,采用该影像可合理概化河道轮廓;其次通过曼宁公式计算河道最大正常水深,以最大正常水深作为下挖深度来概化河道地形。经实测资料可知,叶巴滩与苏洼龙处实测平均流量为1100 m3/s和2000 m3/s,根据DEM可知,从堰塞坝至苏洼龙段河道高程落差大约500 m,河段长235 km,平均坡降0.002,平均宽度50~150 m,根据曼宁公式可计算得到此段河道正常水深为4~8 m,选取最大正常水深作为下挖深度,故整体河道下挖8 m以概化水下河道地形。在河道概化过程中,如果下挖深度比较小,便会导致洪水更容易在河漫滩进行演进,从而对洪水到达时间及流量产生明显的影响;反之,下挖深度比较大,这种影响便会更小,因此选取最大正常水深作为下挖深度来概化水下地形是较为合理的。
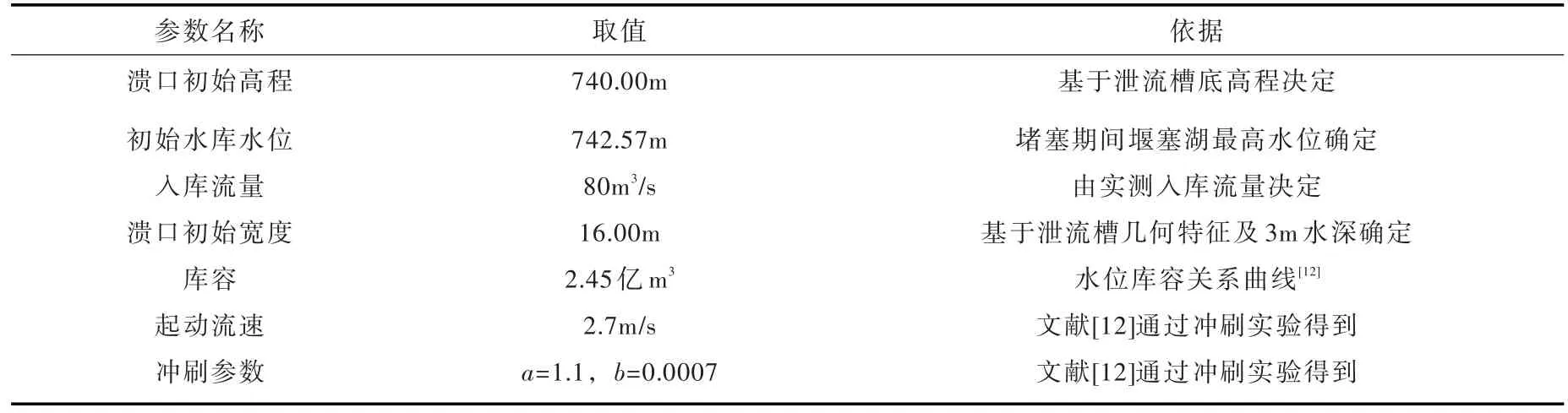
表2 唐家山堰塞湖溃口演变模型计算参数

图17 6月10日耦合模型计算溃坝流量过程线
采用溃口演变模型对溃口流量进行计算,具体计算参数见表3,模拟结果见图22。研究区域模拟网格700万个。由于金沙江断流后下游河道仍有大约200 m3/s的流量,故给予河道200 m3/s的恒定流量作为初始条件。在堰塞坝溃口处,采用源项法将溃坝流量耦合进去,实现上下游的连接,下游边

图18 溃坝洪水上下游不同时刻水深

图19 堰塞坝上下游局部速度矢量图(t=5h)
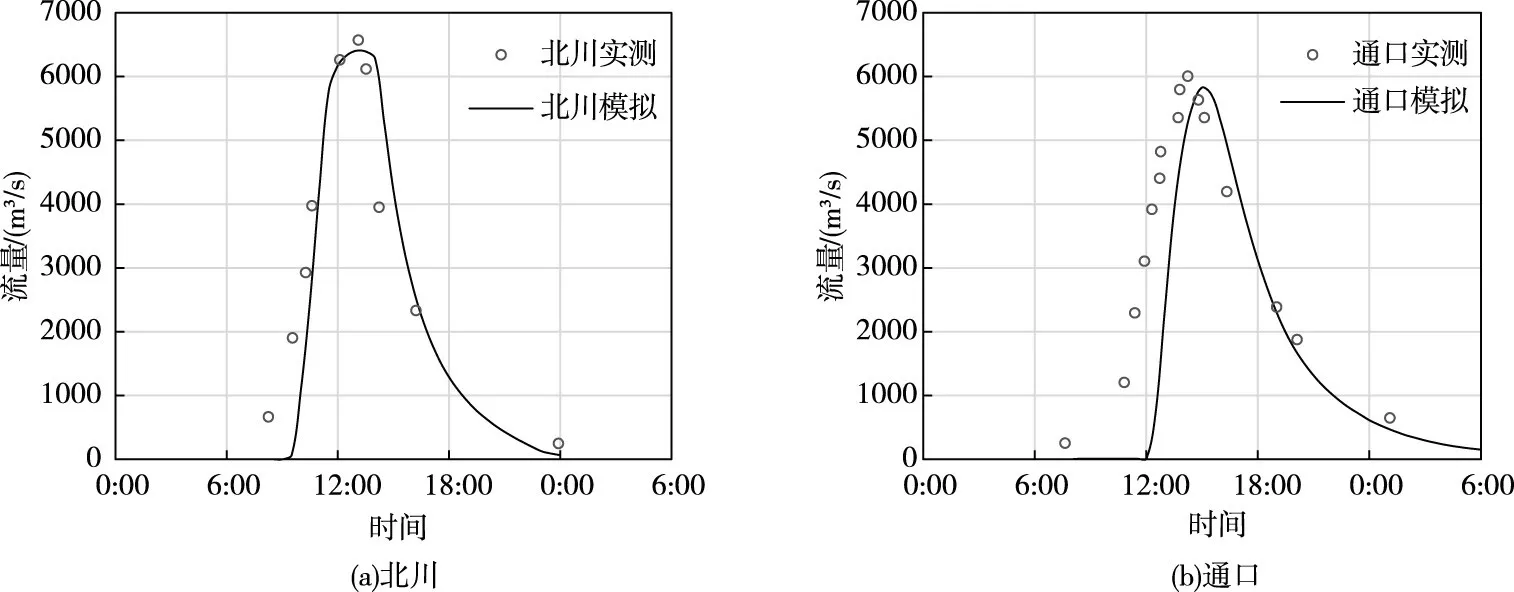
图20 6月10日北川与通口处模拟与实测流量结果

表3 “11.03”金沙江白格堰塞湖溃口演变模型计算参数

图21 研究区域地形图(相对坐标)
4 结论
本文采用源项法将溃口演变模型DB-IWHR与基于GPU加速技术的二维水动力模型进行耦合,建立了一个包含上游库区二维水动力过程、溃口演变和下游淹没区二维洪水演进的高性能全过程耦合模型。该模型有如下优点:(1)所用源项法简单易实现,且具有良好的网格适应性,不需特殊处理计算网格通量的HLLC黎曼求解器;(2)计算溃口流量考虑了溃口的竖向冲刷、侧向扩展过程;(3)采用二维水动力方法模拟溃口上下游区域洪水演进过程,引入GPU加速技术提升模拟效率。界为自由出流的开边界,上游边界为入流边界,入流数据为实测入库流量1500 m3/s,其余边界为闭边界。根据现场实际情况选取曼宁系数为0.02[26],库朗数为 0.5,共模拟 40 h 洪水演进过程。

图22 “11.03”金沙江白格堰塞湖溃坝流量过程线
3.3.2 模拟结果分析 由于下游叶巴滩与苏洼龙处均有在建电站,各电站的防洪安全极为重要,故选取这两处的模拟流量过程与实测进行对比(图23)。其中叶巴滩距堰塞坝54 km,苏洼龙距堰塞坝224 km,模拟耗时2.4 h。模拟研究结果表明,叶巴滩处模拟的洪峰流量比实测小1012 m3/s(3.59%),流量过程整体延迟2 h;苏洼龙处模拟流量过程与实测吻合较好,洪峰流量比实测小614 m3/s(3.13%),在下降阶段比实测稍大。在叶巴滩处产生误差的主要原因仍然在于模拟所用的地形数据精度不高,对主要河道地形的描述与实际河道有很大偏差,尤其是水下地形。
为对比地形概化前后对洪水传播的影响,在未经概化处理的地形上进行洪水传播模拟,模型设置的其余条件保持不变。从图23模拟结果可看出,在未概化处理的地形上,洪水到达时间出现延后及洪峰流量衰减的现象更为严重,这主要是因为未概化处理的地形未能反映河道真实地形,尤其是主河槽部分,地形偏宽浅,与实际窄深河道有偏差,导致模拟洪水在河漫滩演进,模拟水流与地形接触面积增大,模拟水深较浅,从而摩擦阻力较大,能量损失增大,流量减小,洪水到达时间延后。可见,概化后的地形更接近实际地形,对洪水传播的影响相对较小,模拟结果更加合理。
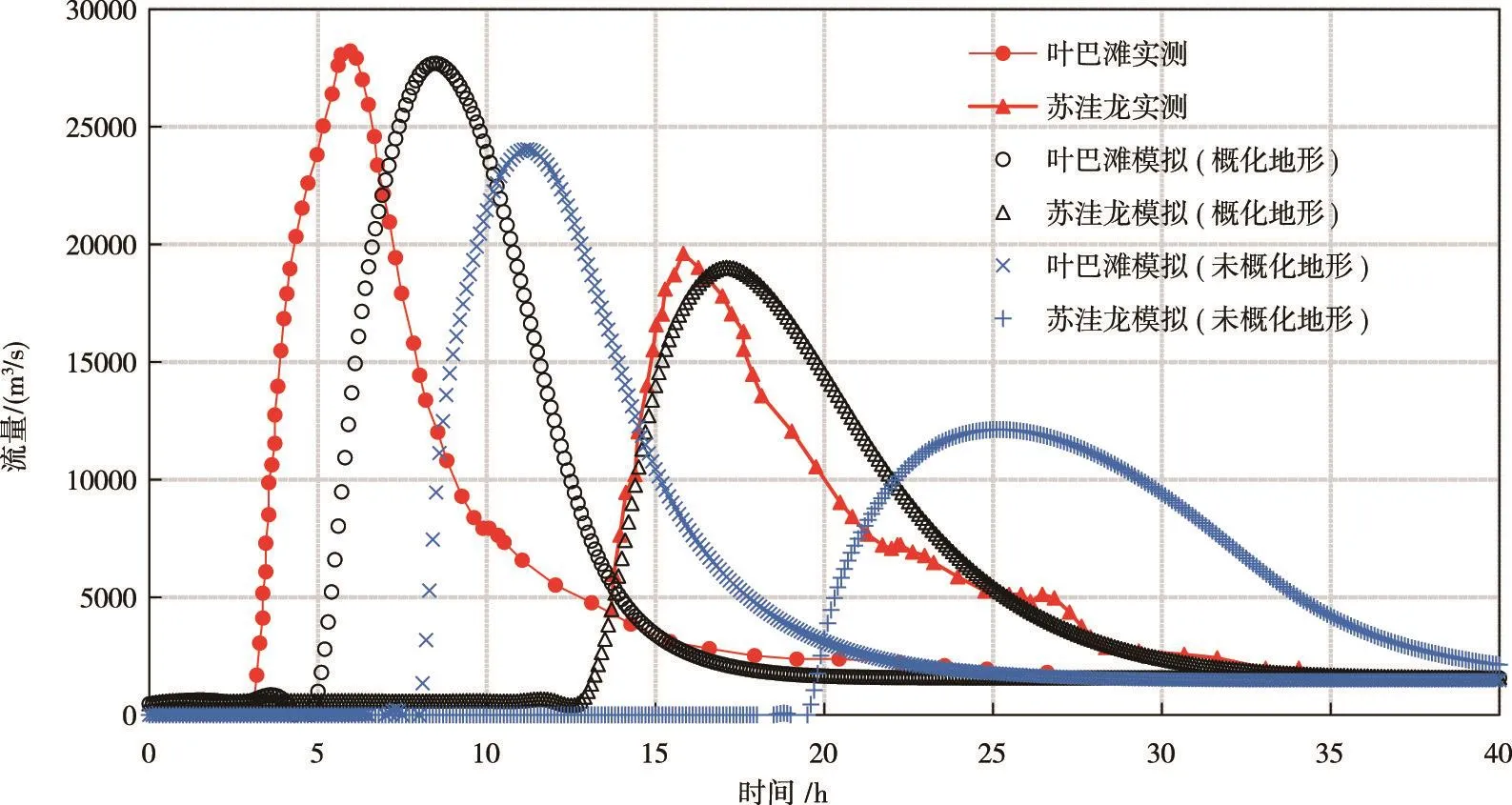
图23 叶巴滩与苏洼龙处模拟与实测流量过程
通过对西班牙托斯大坝溃坝过程及唐家山堰塞湖、金沙江白格堰塞湖的模拟,结果表明,该耦合模型对上游库区、溃口流量及下游演进区的模拟效果较好,模拟结果与实测值吻合度较高,计算效率较快,综上,基于源项法的耦合模型可实现对土石坝、堰塞坝溃坝等灾害事故的合理高效预测,为应急抢险工作提供有力支撑。
