圆弧刀廓加工螺旋锥齿轮的全齿面分区修形
2019-12-05陈义忠严宏志艾伍轶伊伟彬
陈义忠,严宏志,艾伍轶,邓 辰,伊伟彬
(1.中南大学 高性能复杂制造国家重点实验室,长沙 410012;2.中南大学 机电工程学院,长沙 410012;3.中南大学 轻铝合金学院,长沙 410012)
0 引言
刀具修形是一种高效、简便的齿面修形方法。常见的刀廓修形有:直线刀廓、抛物线刀廓和圆弧刀廓。圆弧刀廓的刀具在展成齿面时,齿廓方向修形量增大,可有效避免在轮齿根部和顶部处形成的边缘接触[1]。但圆弧刀廓在齿根和齿顶处修形会产生失配[2],导致传动误差幅值增大。针对存在的这个问题,需要对圆弧刀廓修形的齿面进行近一步修形优化。
国内外学者对齿面修形做出了许多研究。苏进展[3,4]提出基于Ease-off的弧齿锥齿轮齿面修形优化方法,沿接触迹和啮合线对小轮齿面进行双向修形,并获得目标齿面;王会良[5]将齿面划分为9个区,提出了斜齿轮沿齿长和齿廓方向上的拓扑修行方法,建立了修形齿面;聂少武[6]研究了圆弧刀廓修形对齿面形状的影响,并得出合理的圆弧刀廓半径可降低边缘接触;STADTFELD[7]设计了4段刀廓新刀具,可提高摆线锥齿轮的啮合性能;方宗德[8]提出基于齿面曲率修正方法的高阶传动误差设计,设计出高重合度弧齿锥齿轮,改善了齿轮副的啮合平稳性;唐进元[9]基于主动设计方法,由局部综合法求得满足预设定传递误差曲线且容差性较好的一组小轮加工调整参数。
本文研究了圆弧刀廓加工小轮齿面的全齿面分区修形,主要包括:首先利用圆弧刀廓将小轮齿根、齿顶处划分为两个区域,其次基于多段抛物线分区修形将齿面主要工作部分划分为大端、中间区域和小端;然后根据预设的接触迹线夹角和分区修形参数,对圆弧刀廓加工后的齿面重新设计,以获得满足预设性能的目标齿面。最后反求出一组优化后的小轮机床加工参数,并通过加载接触分析方法验证了全齿面分区修形优方法的有效性。
1 双重螺旋法加工螺旋锥齿轮副建模
1.1 圆弧刀廓齿面数学模型
本文只对双重螺旋法加工、圆弧刀修形的小轮齿面建模,大轮采用直线刀廓成形法[10]。
如图1(a)所示,a部分为刀廓的主要切削部分,圆弧半径为R1;b部分为刀廓展成齿根圆角部分,圆弧半径为ρ。坐标系σ1'={OO1;i’,j,k}与小轮刀盘固连,Oo1为刀盘中心,坐标轴k为刀盘轴线。M1、M2为小轮工作面、非工作面参考点,S01为沿参考点处切线从齿根到M2点的距离,S1为沿参考点处切线从齿顶到M2点的距离,α1为刀具齿形角,W1为刀顶距,刀盘半径为rt1(外刀半径为r1c,内刀半径为r1d)。图1(b)、(c)分别为小轮内、外刀产形面示意图,其中I表示刀倾角,θ1为刀盘相位角。

图1 小轮圆弧刀廓及其产形面
刀尖半径可由下式计算:

将a部分的产形面以矢量形式表示为:

式中的双符号,上面的符号对应外刀(工作面),下面的符号对应内刀(非工作面)。由式(2)可得到产形面的法矢为:

如图2所示,建立坐标系σ1={O';i1,j1,k1},其中,O'是机床中心,i1-j1平面为机床平面同,O1为小轮设计交叉点,Z1为径向刀位;q1为角向刀位;XB1为床位;X1为轴向轮位;E1为垂直轮位;I为刀倾角,J为刀转角;δM1为小轮轮坯安装角。产形轮的轴向与k1轴所在直线的方向相同,故单位矢量以k1=[0 0 1]T表示。
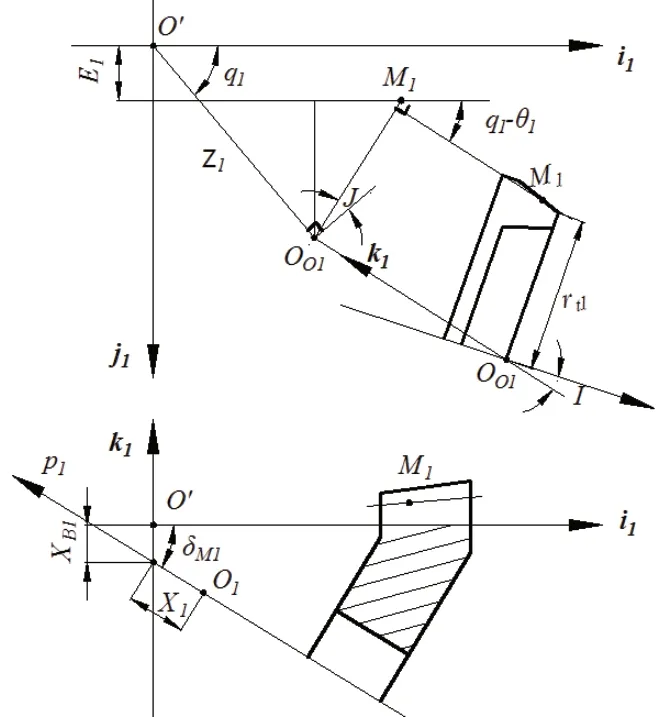
图2 小轮加工坐标系
将小轮产形面方程位置矢量表示在机床坐标系σ1中:
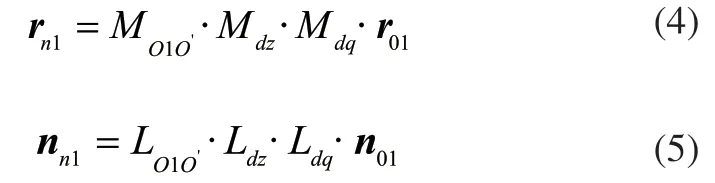
其中,MO1O'、Mdz、Mdq为中间坐标系变换矩阵[11];LO1O'、Ldz、Ldq分别对应变换矩阵的三阶主子式。
则小轮交叉点O1到机床中心O'的矢量可表示为:

产形面与小轮齿面完全共轭,以小轮设计交叉点为原点,则小轮齿面上任一点的位置矢量可表示为:

1.2 齿轮副三维模型的建立
以1对准双曲面齿轮副为研究对象,大、小轮基本参数及加工参数如表1、表2所示。将求解所得的大、小轮齿面空间坐标点导入Pro/E中,得到大、小轮齿面。根据设计要求将大、小轮进行安装,得到螺旋锥齿轮副三维模型,如图3所示。

表1 齿轮副基本参数

表2 齿轮副加工参数

图3 齿轮副三维模型
2 全齿面分区修形方法研究
本文提出的全齿面分区修形是将圆弧刀廓修形和主动设计相结合的方法,将整个齿面划分成五个区,既可有效避免在轮齿根部和顶部处形成的边缘接触,又起到对齿面沿齿长方向、齿廓方向和对角方向全方位的预控修形。
图4为小轮修形区域示意图,其中①为中间区,利用多段抛物线沿齿面啮合线修形,通过预控接触迹线方向、接触椭圆长半轴长度、传动误差对该区域进行齿面拓扑优化;②、③为利用圆弧刀廓分别对小轮齿面的齿根、齿顶进行修形的区域。④、⑤为利用多段抛物线分区修形分别对小轮齿面大端、小端进行修形的区域。
2.1 齿面啮合性能主动设计
预设大轮传动误差曲线和接触区参数,可求出与大轮完全共轭的小轮齿面。完全共轭齿面[12]相当于分区修形过程中的基准平面,然后在其基础上修形可以得到满足预设性能的小轮目标齿面。
如图5所示,横坐标φ1为小轮转角,纵坐标δφ2为大轮传动误差,b和b'为齿对间传动过程中的啮合转换点。2π/z1为单个啮合周期转角;z1是小轮齿数,δT1为转换点的传动误差。
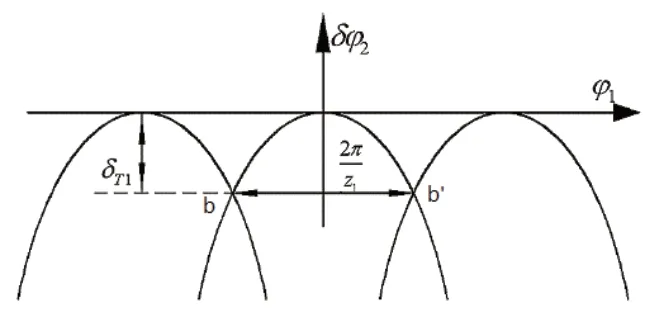
图5 预设传动误差曲线
传动误差曲线可表示为:
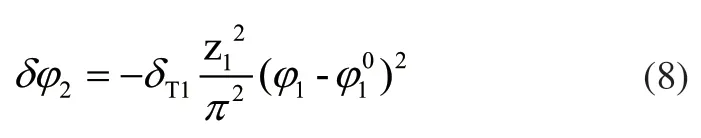
接触区的大小、位置直接影响齿轮副的啮合性能。如图6所示,M为齿面参考点,虚线区域为接触区,接触迹线与节锥线的夹角用η表示,接触椭圆长半轴长度用a表示。

图6 接触迹线示意图
2.2 多段抛物线分区主动设计
多段抛物线分区主动设计为沿啮合线方向上的修形。如图7所示,以啮合线所在的直线为x轴,以接触迹线IJ与啮合线的交点M为坐标原点,以过M点垂直于啮合线的直线为y轴,建立oxy坐标系。
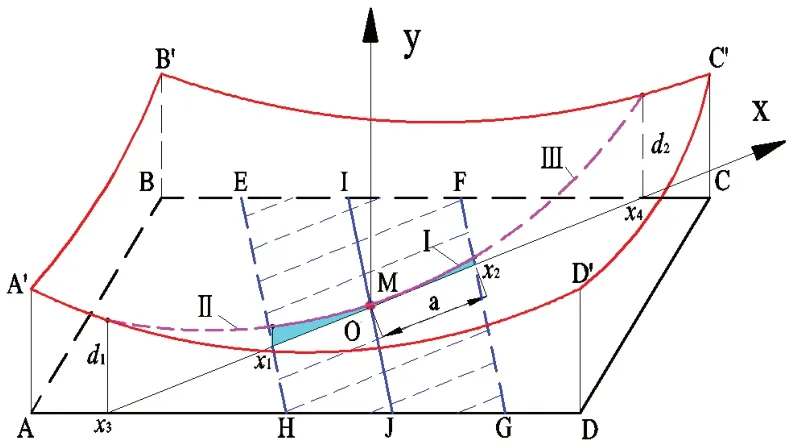
图7 多段抛物线分区修形示意图
其中ABCD表示完全共轭齿面,A'B'C'D'为修形后的目标齿面。多段抛物线分区将齿面分为三个区域:大端、小端和中间区;在中间区域内(EFGH)沿抛物线Ⅰ进行修形,在小端区域内(ABEH)沿抛物线Ⅱ进行修形,在大端区域内(CDGF)沿抛物线Ⅲ进行修形。在oxy坐标系中,x3表示小端最远齿面点,x4表示大端最远齿面点,x1x2表示齿面接触区横向长度,d1、d2分别表示小端、大端最大修形量。
沿啮合线方向的齿面法向修形量可表示为:

其中ζ为弹性变形量,一般取为0.00635mm[13],k为齿面不同的修形区域,m为修形曲线系数;Ⅰ,Ⅱ,Ⅲ段修形曲线可根据不同的修形要求,通过预控大端、小端的最大修形量d2、d1,反求出不同的修形系数m值来实现。
另外,要保证修形齿面连续可导,还应该满足:

3 算例分析
3.1 预设参数
将圆弧刀廓修形的小轮齿面定义为原始组,将全齿面分区修形的小轮齿面定义为优化组,加工参数如表2所示。对原始组齿面进行接触分析,得到原始组接触迹夹角。优化组接触迹线夹角大小和分区修形预设参数如表3、表4所示。

表3 齿面接触迹夹角η
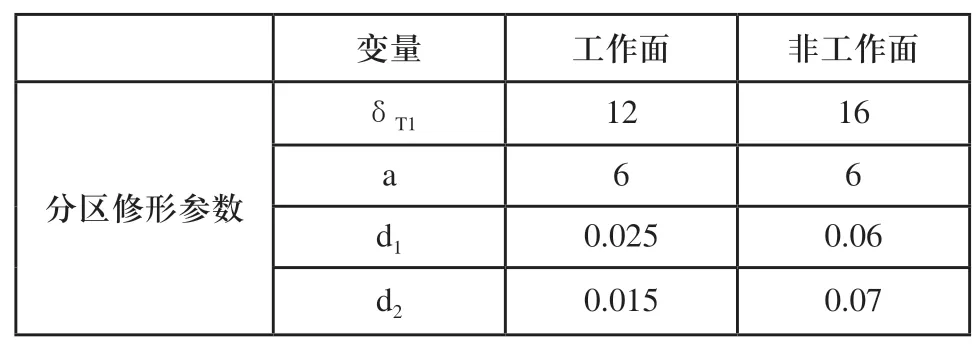
表4 优化组分区修形参数
在表4中,其中δT1单位为秒(″),其余单位为毫米(mm)。
3.2 全齿面分区修形目标齿面
原始组ease-off图如图8和图9所示,优化组齿面ease-off图如图10、图11所示。

图8 原始组的齿面(工作面)

图9 原始组的齿面(非工作面)

图10 优化组的目标齿面(工作面)

图11 优化组的目标齿面(非工作面)
3.3 加工参数反求
对比目标齿面与原始组的齿面,可得两齿面间的法向偏差。而齿面法向偏差与加工参数改变量的关系如下式所示[14],此方程为超静定非线性方程组,运用最小二乘法,求得对应的机床加工参数调整量,从而得到最终的机床加工参数。

其中,δφk为加工参数调整量,Skm为机床加工参数对齿面点的敏感系数,δdm为齿面法向偏差。
基于以上所述,可得优化组对应的机床加工参数如表5所示。

表5 优化组机床加工参数
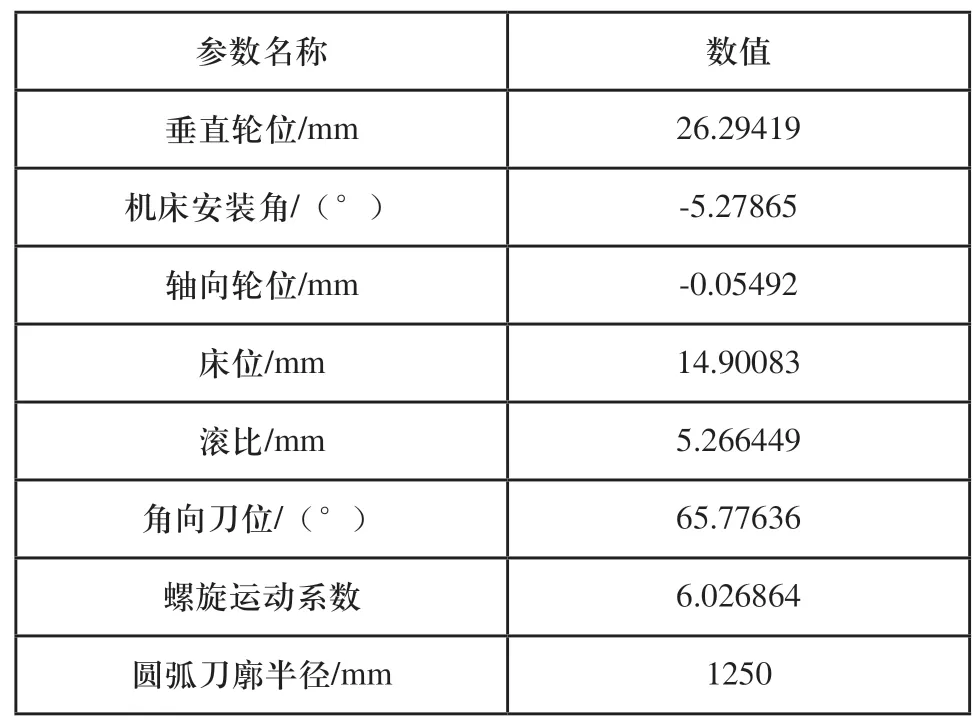
续(表5)
4 有限元加载分析(LTCA)
4.1 重合度分析
重合度是影响齿轮传动啮合性能的主要因素,是判断齿轮传动连续性及传递载荷均匀性的关键指标[15]。重合度是指小轮单齿从进入啮合到退出啮合所转过的角度Tc与Tz的比值。因此,齿面重合度可以表示为:

其中,Tz是小轮的啮合周期,为图5中小轮从b点到b'点转过的角度。
在齿轮副动态啮合过程中,小轮旋转的角度与小轮齿面瞬时接触应力所对应的时间是成正比的[16]。T表示某一单齿整个啮合过程所经历的时间,T1表示上一单齿从开始啮合到下一单齿进入啮合所经历的时间,故齿面重合度也可以表示为:

基于所求得优化组与已知的原始组齿轮参数建立对应的齿轮副模型,并导入abaqus进行有限元仿真,其中齿轮材料都为16Cr3NiWMoVNbE。设置小轮转速600r/min,大轮负载扭矩为600Nm,分别对两组齿轮副进行有限元动态啮合仿真,得到齿轮副啮合过程中载荷对接触力随时间变化的分配图,如图12、图13所示。
分析原始组第五齿的啮合过程:图12中第五齿进入啮合的时间为3.495s,完全退出啮合的时间为3.710s,在3.626s时,第六齿开始进入啮合,可知其重合度为1.64;同理可知,优化组的重合度为1.73,结果如表6所示。

图12 原始组啮合过程接触力分配图

图13 优化组啮合过程接触力分配图

表6 两组齿轮副的重合度比较
4.2 传动误差分析
传动误差曲线的波动程度可反映出齿轮副在受载条件下的动态性能,其波动程度越小,振动和噪声越小,齿轮副传动越平稳[17]。在abaqus仿真环境中可得到两组齿轮副的传动误差,如图14和图15所示。其中,P-P表示峰峰值,p-p表示单齿峰峰值。
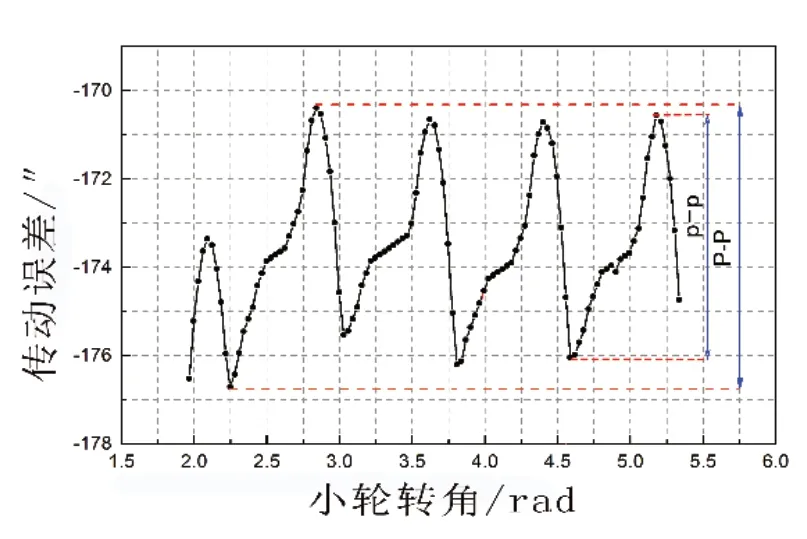
图14 原始组传动误差
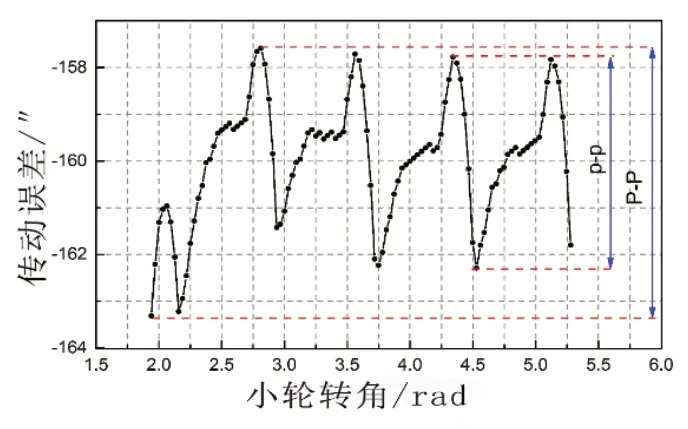
图15 优化组传动误差

表7 传动误差分析
分析图14和图15可得表7,可知:优化组传动误差的均值、P-P值和p-p值相对于原始组分别降低了7.4%、12.7%、18.15%。
4.3 齿面接触应力分析
对比分析图16和图17可知:原始组齿面间最大接触应力为1799MPa。优化组齿面间最大接触应力为1776MPa。优化组相对原始组齿面最大接触应力降低了1.3%。

图16 原始组齿面啮合区

图17 优化组齿面啮合区
5 结语
1)基于双重螺旋法的螺旋锥齿轮齿面创成原理,推导了圆弧刀廓加工小轮齿面模型;并将齿面划分为五个区域,提出了全齿面分区修形的主动控制方法。
2)通过预设接触迹夹角和分区修形参数,求出了全齿面分区修形后的目标齿面,并反求出优化后的机床加工参数。
3)通过全齿面分区修形主动设计,提高了齿面重合度,降低了齿轮副的传动误差幅值、齿面最大应力,弥补了由于圆弧刀廓修形失配引起的传动误差的波动,提高了齿轮副的运行平稳性。
