地下物流系统对集装箱运输网络的影响分析

丁 一，王玉婷，梁承姬

（上海海事大学物流科学与工程研究院，上海 201306）

0 引言

随着世界集装箱量的增长，港口行业面临着不断增加的货运量的压力，交通拥堵问题日益加剧。2017年，上海港的集装箱吞吐量达到4023万TEU，增长8.4%，再次成为全球最大的集装箱港口。作为上海港的主要集装箱港区，2017年外高桥港区突破了1960万TEU，成为世界上单一港区吞吐量最大的一个港区。按照外集卡一次运输两个20英尺标准箱，平均每月有331924辆外集卡进出外高桥港区。过多的外集卡运输加重了交通拥堵。因此，提高交通网络的运输能力是解决当前问题的关键。

目前，拓展现有的交通运输系统是提高运输能力的一种方法，属于交通网络设计问题。对于交通网络设计，Miandoabchi等[1]研究了城市离散交通网络设计问题，以新建道路为交通规划方案，建立了多目标规划模型，使用模拟退火算法解决问题。Liu等[2]考虑具有随机用户均衡约束的离散网络设计问题，减少交通网络设计的随机性。Wang等[3]在假定每条道路的容量和建设成本都是基于车道数量的情况下，设计了新建车道和扩展道路容量两种方案。Farvaresh等[4]考虑通过扩建道路容量来提高车辆通行能力，构建以最小化系统阻抗为目标的混合整数线性规划模型，也提出扩展现有的交通系统的局限性。

只扩展现有的交通运输系统无法满足日益增长的集装箱运输需求，为了减少货运增加导致的空气污染和交通拥堵，许多国家正在研究可持续的运输方式[5,6]。因而，地下物流运输系统应运而生。地下物流运输系统是一种使用隧道或管道运输货物的地下运输系统[7]。与集卡运输相比，地下物流运输系统的限制较少。

对于地下物流，目前主要有美国纽约港、新泽西港、日本东京港、比利时安特卫普港和德国鲁尔工业区进行了地下集装箱运输系统的技术研究[8～11]。2006～2008年，上海市政院研究了上海发展地下集装箱运输系统的技术和经济可行性，提出了洋山港区至外高桥港区、洋山港区至芦潮港物流园区的可能地下集装箱路线[12]。

从以上研究可以看出，对于地下物流，大多数文献研究建造技术，很少有研究引入地下物流系统对交通，货运，环境和相关问题的影响。大多数研究集中在城市交通网络设计问题，很少有研究在现有交通网络中创新交通方式。因此，本文着重研究引入地下物流系统对集装箱运输网络的影响。

1 问题描述

目前，集装箱主要依靠公路进行运输。由于集装箱货运量的增加，外集卡运输集装箱的次数明显增加，加剧了公路运输压力，码头及环线道路拥堵现象严重，交通事故也频繁发生。只扩展现有的公路容量或者新建公路，无法满足今后集装箱运输需求，将面临严峻的交通压力。同时，环境问题突出，大量外集卡尾气排放造成空气污染。

因此，本文提出引入地下物流系统对集装箱交通网络进行优化。地下物流系统由嘉定货运综合枢纽，地下物流通道和外高桥港区后方物流综合枢纽组成。外集卡通过公路运输将集装箱运至嘉定货运综合枢纽，再经由场桥和内集卡将集装箱运送至地下物流通道入口，由AGV小车运送至外高桥码头。原先通过公路分散运输的集装箱被吸引通过地下物流系统运输，改变了集装箱运输网络的交通流状态，集装箱则更集中通过地下物流通道运输，减轻公路运输压力。将引入的地下物流系统抽象成地下物流通道和原有的公路运输网络结合形成新的集装箱运输网络作为本文研究的对象，如图1所示。

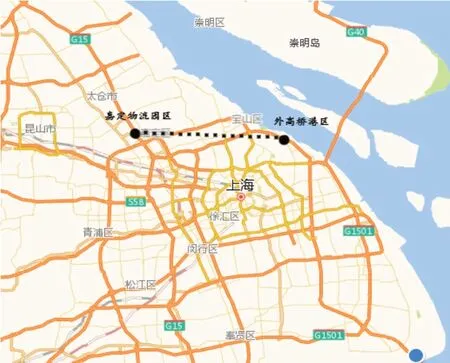
图1 引入地下物流系统后的集装箱运输网络图

结合地下物流的特征，做出以下假设：1）外集卡司机总是选择阻抗最小的道路运输集装箱；2）地下物流通道出入口与嘉定物流园区和外高桥码头已衔接；3）不考虑地下物流通道投资建设问题，假设地下物流通道已经建成；4）暂不考虑水路和铁路运输集装箱。

2 模型建立

下面将建立针对地下物流系统的集装箱运输网络模型，综合考虑系统阻抗和二氧化碳排放量两个指标，构建多目标规划模型。交通阻抗通过阻抗函数来描述，地上路段采用BPR（Bureauof Public Roads）函数，而地下物流通道的阻抗取决于AGV小车速度和地下物流通道长度[13]。

2.1 符号说明

集合和参数：A1为集装箱交通网络中地上路段的集合；A2为集装箱交通网络中地下路段的集合；E为集装箱交通网络中所有路段的集合；Rw为OD对w的所有路径集合；Q为OD需求有界集合；xa为路段或地下物流通道的集装箱运输量；la为路段或地下物流通道的长度；va是路段或AGV小车的行驶速度；Er为外集卡二氧化碳排放系数；Euls为AGV小车二氧化碳排放系数；ca为地上路段或地下物流通道的实际通行能力；为地上路段的阻抗函数；为地下物流通道的阻抗函数；α和β是参数，其值设为0.15和4；qw为OD对w的集装箱运输需求量；为OD对w的集装箱运输需求量的“名义值”；为OD对w的第k条路径的集装箱运输量；σak为0～1变量，当且仅当地上路段或者地下物流通道在路径k上时为1，否则为0。

2.2 数学模型

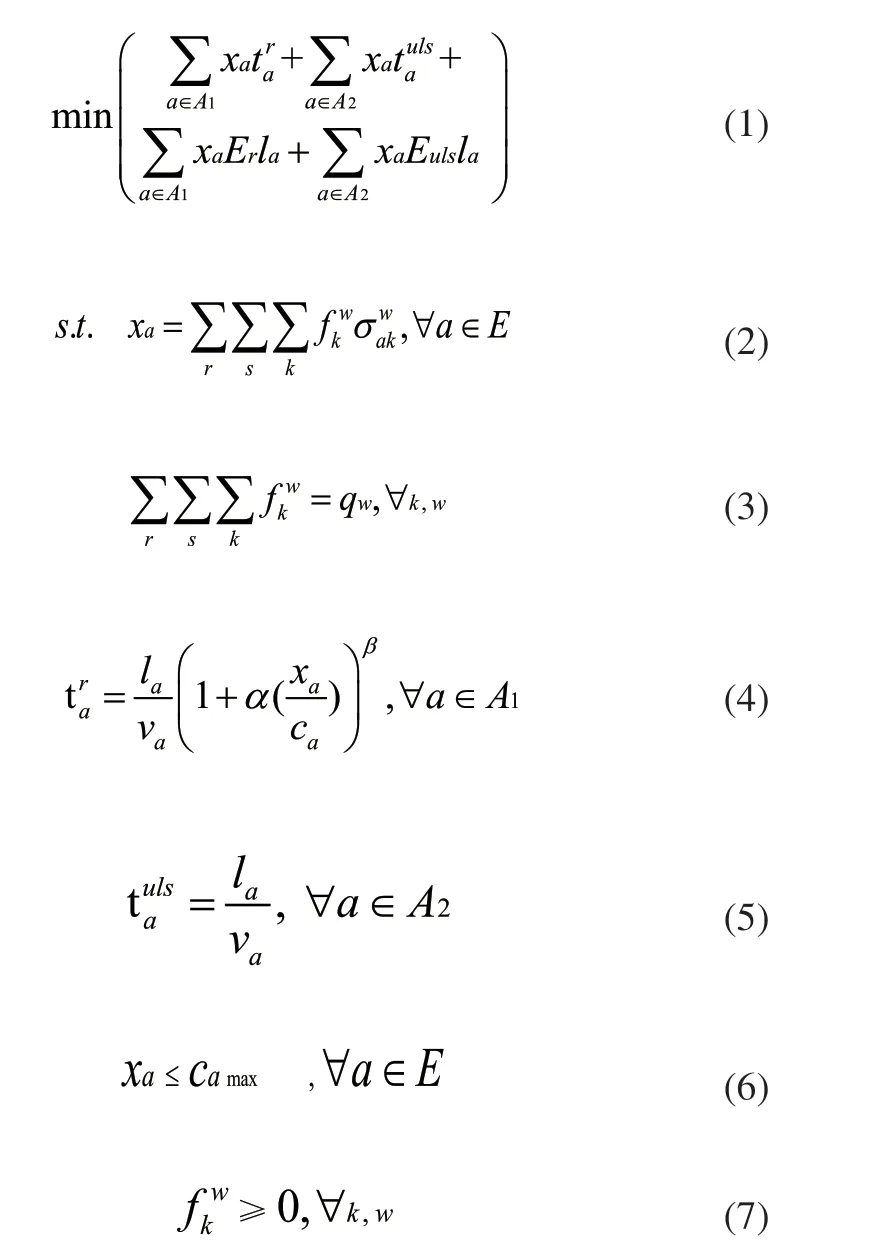
目标函数（1）最小化地上路段和地下物流通道的的总系统阻抗和二氧化碳总排放量。条件约束（2）表示路段a的集装箱运输量和路径集装箱运输量的关系。条件约束（3）表示路径集装箱运输量和总集装箱运输量的关系。条件约束（4）、（5）分别表示路段和地下物流的阻抗函数。条件约束（6）表示路段a的流量不能超过其最大通行能力。条件约束（7）表示路径k上的集装箱运输量大于等于0。

2.3 模型优化

在交通网络中，OD需求具有不确定性，鲁棒优化是处理不确定性问题的重要方法。针对集装箱运输需求的不确定性，本文利用一个有界集合来表示集装箱运输需求的不确定性，得到：

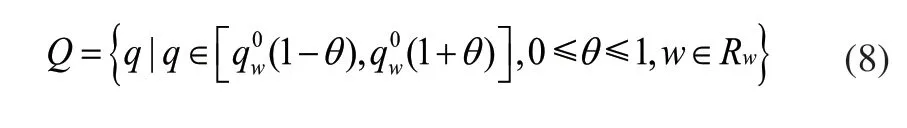
优化后的数学模型为：

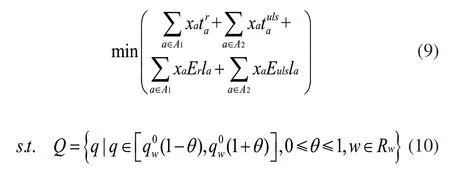
其余约束同式(2)～式(7)。

3 蚁群算法设计

蚁群算法最早是由Dorigo等[14]提出，特别适用于组合优化问题。针对本文建立的多目标规划模型，基于蚁群算法的思想，对系统最优情况下的集装箱运输量分配问题进行求解。

3.1 参数设置

1）能见度：能见度以距离来衡量，本文考虑以集装箱运输量作为变量，即：

2）信息素：针对本文要解决的问题，考虑交通网络中的地下物流通道和原有路段的通行能力，引进阻抗函数，因此第k只蚂蚁在路段和地下物流通道的信息素量公式调整为：

式中，E表示蚂蚁循环一次释放的信息素总量。随着时间推进，蚂蚁遗留的信息素逐渐蒸发。因此，当所有蚂蚁完成一次集装箱运输量分配后，信息素浓度需要进行实时更新，即：

其中，ρ(0<ρ<1)表示信息素的挥发程度。

3）转移概率：在最初t=0时刻时，各路径的信息素都相同，则蚂蚁选择路径的概率相同。但是随着一次循环完成后，路段上的信息素浓度和能见度都发生变化，所以结合上面对信息素浓度和能见度的公式的调整，将蚂蚁的转移概率调整为：

其中，a-allowedk表示蚂蚁下一步选择的路段，α为信息素重要程度因子，β为能见度重要程度因子。

3.2 算法步骤

Step1：设置算法参数，取α=1，β=2，ρ=0.7，Q=100，将集装箱运输量作为蚂蚁数量m。输入路网信息，并且初始化路段集装箱运输量。

Step2：将m只蚂蚁分成两批进行集装箱运输量分配。第一批蚂蚁放在路网起点上，随机选择路段，完成一次分配，计算此时道路的上的蚂蚁数，即路段集装箱运输量和阻抗函数，并且根据公式更新蚂蚁信息量，得到路段初始信息素。

Step3：从第二批蚂蚁开始，蚂蚁通过转移概率来计算任意相邻路段的行走概率并转移到下一节点，计算此时路网中路段蚂蚁数和阻抗函数，记录当前的最优解，并且更新信息量。

Step4：更新后的信息素量若满足路段最大能力的限制，则进行下一步，否则终止。

Step5：计算目标函数值，即系统的阻抗函数值和碳排放量，找出路网系统最优解。

Step6：若m只蚂蚁全部循环一次结束，转至7），否则转至3）。

Step7：满足最大循环次数，则循环结束输出最优解，否则转2）。

4 算例分析

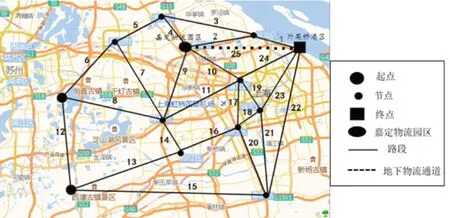
图2 交通网络图

图2所示交通网络中，有13个节点，25条路段，其中包括嘉定货运综合枢纽到外高桥码头之间的地下物流通道。地下集装箱运输网络为引入地下物流系统后的网络。统计2016年外高桥码头8月到10月的集装箱运输量，总计2089317TEU。假设AGV小车的速度为60km/h，集卡速度为45km/h。初始数据如表1所示。

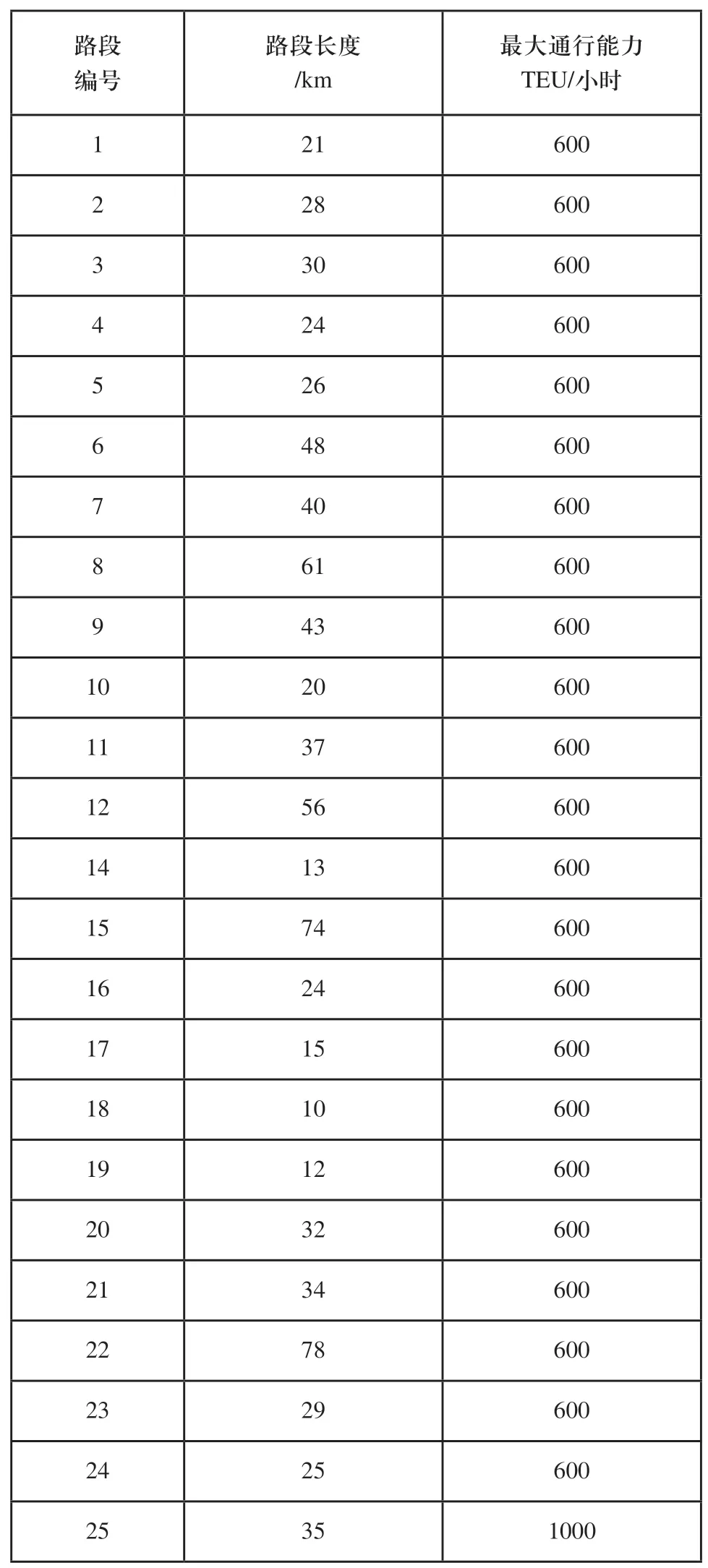
表1 初始数据

本文引入平均度和平均路径长度来评价交通网络结构，并且考虑加权网络。平均度反映网络连通性，计算公式为式中，Nj是节点i的相邻节点的集合，wij为路段集装箱运输量，n1为网络中节点数量。平均路径长度反映网络传输效率，计算公式为L=1/n2(∑a(ta/xa))，由Qin[15]等提出，式中n2表示交通网络中路段的数量。

4.1 算例求解

在固定OD需求和基本通行能力，并且公路集装箱运输网络二氧化碳排放系数为0.3kg/km，地下集装箱运输网络二氧化碳排放系数为0.2kg/km的情况下，使用MATLAB（R2014b）对多目标规划模型进行求解，得到的结果如表2、图3所示。

表2 结果对比

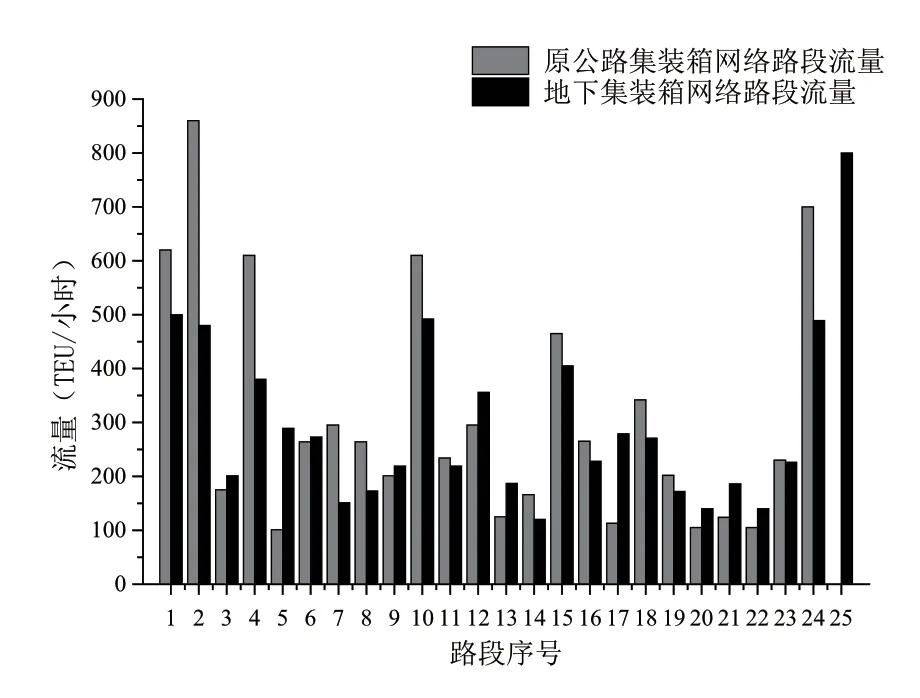
图3 流量对比

由表2可看出，地下集装箱运输网络系统阻抗和二氧化碳排放量分别减少40%和44%，在缓解交通拥堵和减排上效果明显。优化后的网络平均度增加到720，平均路径长度降低为245，地下集装箱运输网络的连通性和整体性增强，传输效率得到提高。同时，蚁群算法求解时间在20s左右，有较好的求解效果。

如图3所示，集装箱运输量在地上路段和地下通道上得到合理分配。原公路集装箱运输网络中路段1，路段2，路段4，路段10和路段24的集装箱运输量已超出给定的600TEU/小时，明显造成交通网络拥堵。优化后，地下集装箱运输网络中，这些路段的运输量降低至给定的范围，地下物流通道承担更多的运输量，明显减少拥堵。

4.2 灵敏度分析

为进一步分析引入地下物流对集装箱运输网络的影响，从OD需求，通行能力和二氧化碳排放这三个方面进行灵敏度分析。

4.2.1 OD需求变动的影响分析

本节通过控制OD需求不确定范围的参数θ来分析对集装箱运输网络的影响。

图4 不同参数下系统阻抗和网络测度值

图4显示了在集装箱运输需求变动的情况下交通网络的系统阻抗增加，但地下集装箱运输网络的增量更小。θ取0.3，0.6和0.9时，公路集装箱运输网络的系统阻抗分别为7000小时，7260小时，7600小时。地下集装箱运输网络的系统阻抗分别为4250小时，4325小时，4400小时。此时，地下集装箱运输网络的阻抗增量更小，需求的变动对其影响更小，使其更稳定。对交通网络拓扑结构而言，地下集装箱运输网络的平均度更大，平均路径长度更小，网络的连通性、可达性、传输效率增强。在需求变动的情况下，地下物流通道凸显其可达性强和运输效率高的优势。

4.2.2 通行能力变动的影响分析

通行能力受到很多因素的影响，如天气、道路拥堵状况等，将会造成道路通行能力折减，本文采用式CP=CBf1f2f3…fn进行修正，f为折减系数。假设f=1代表固定通行能力情况，f=0.9代表上下班高峰期对道路通行能力的折减系数，f=0.8代表节假日对道路通行能力的折减系数，f=0.7代表恶劣天气对道路通行能力的折减系数。通过不同的折减系数来评估通行能力对集装箱运输网络的影响，如图5所示。

由图5可以看出，恶劣天气、节假日、上班高峰期对原公路集装箱运输网络影响较大，系统阻抗最高达到7398小时，系统阻抗明显增加。而对于地下集装箱运输网络，系统阻抗增量很小，对其影响较小，地下物流通道应对天气和道路变化的优势明显，交通网络的抗毁性更好。在天气和道路因素变化造成拥堵的情况下，外集卡司机更愿意选择有地下物流通道的路线，此时网络的连通性和可达性更好。

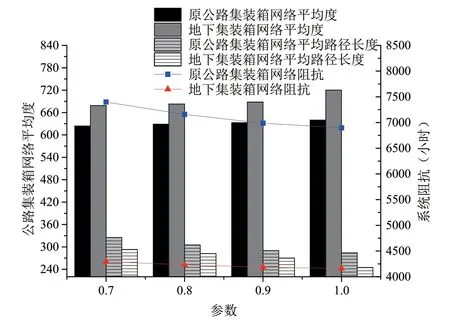
图5 不同折减系数下系统阻抗和网络测度值

4.2.3 二氧化碳排放的影响分析

参照国家温室气体清单指南和上海电力碳排放系数，将高峰期柴油二氧化碳排放系数设为1.1kg/km，非高峰期为0.9kg/km。将高峰期电力二氧化碳排放系数设为0.4kg/km，非高峰期为0.3kg/km。本节对高峰时期和低峰时期的二氧化碳排放量进行比较，来分析优化前后集装箱运输网络减排效果，得到如表3和图6所示结果。

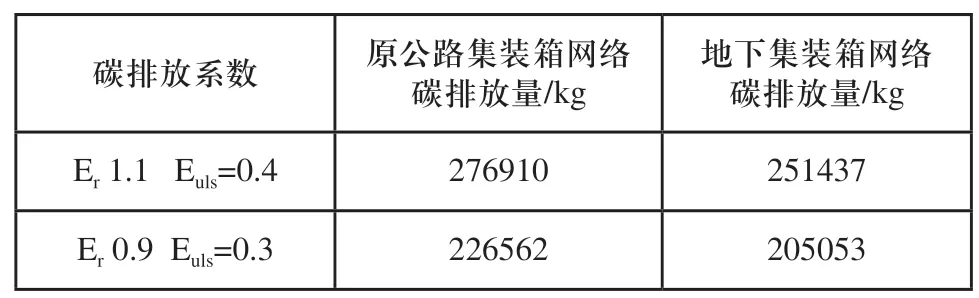
表3 碳排放量结果对比

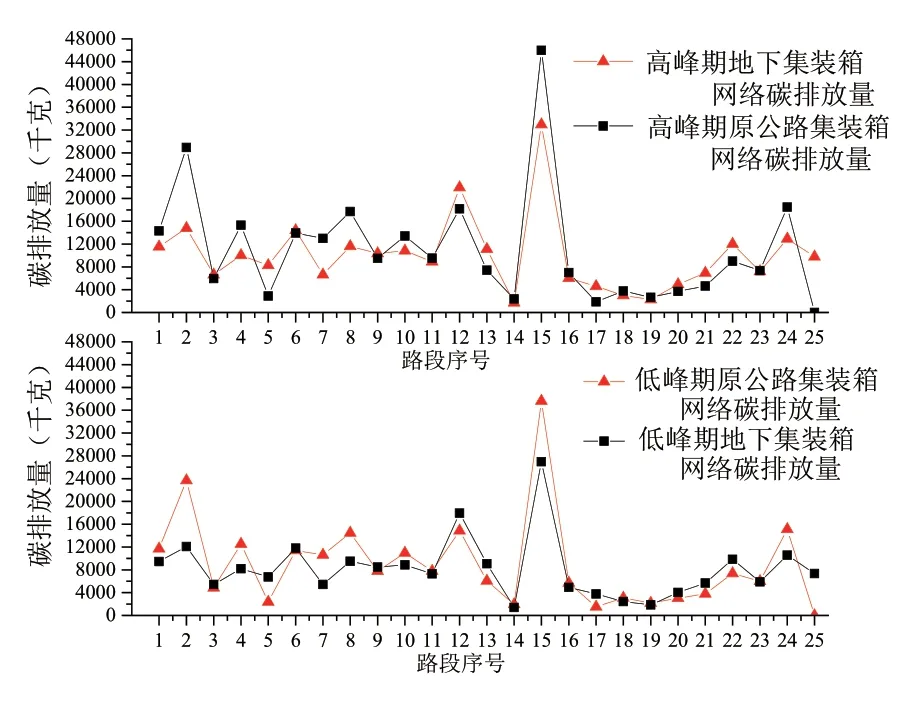
图6 路段碳排放量

表3所示为优化前后总的二氧化碳排放量。无论是在高峰期还是非高峰期，地下集装箱运输网络的碳排放量都比原公路集装箱交通网络小，高峰期碳排放量减少25473千克，非高峰期减少21509千克。地下集装箱运输网络各路段碳排放量分布更加均衡，地下物流通道碳排放量相对较小，如图6所示。从长远角度考虑，地下物流运输以电力为动力，而集卡运输以柴油为动力，地下物流通道不仅可以减少碳排放量，而且可以减少能源消耗，环境效益将会越来越明显，符合可持续性发展要求。

5 结语

本文针对引入地下物流系统后的集装箱运输网络，构建了考虑系统阻抗和碳排放的多目标规划模型。在算例分析中，对原集装箱运输网络和地下集装箱运输网络进行对比分析。结果表明，地下物流运输系统能有效减少港口拥堵，缓解了集装箱运输压力。在环境污染方面，地下物流运输系统碳排放量明显减少，从长远角度考虑，其环境效益可观。同时，地下物流系统不受天气等外界因素的影响，运输更加稳定，实现了高效、安全、无中断物流运输。通过本文研究，为优化集装箱运输网络提供了一种方法。