穿纤维微穿孔板吸声系数的有限元仿真
2019-12-04李晨曦何立燕
李晨曦 胡 莹 何立燕
(中国商飞上海飞机设计研究院 上海 201210)
0 引言
随着科技的发展,日常生活中的噪声污染也日益严重。因此,人们对降噪吸声产品的需求也日益增高。常用的吸声材料多是多孔性纤维或泡沫材料,如玻璃棉、人造纤维、开孔泡沫材料等。这些材料主要通过气流流经孔隙时的黏滞效应和内摩擦效应等将声能转化为其他类型的能量,以此达到吸声的作用。这类产品吸声频带宽、价格便宜,广泛地应用于汽车制造业、厅堂声学设计等方面。但多孔性材料容易产生粉尘污染,这限制了多孔性材料在医院、食品加工厂、微电子产业等方面的应用[1]。而马大猷院士[2]提出的微穿孔板吸声结构可以弥补多孔材料在这方面的缺陷。
经典的微穿孔板吸声结构的薄板表面分布着微小穿孔,孔径常在1 mm左右。由于黏滞效应,这样的微孔可以提供足够高的声阻,从而提供有效的吸声效果[3]。但与传统的纤维或泡沫材料相比,微穿孔板的吸声频带较窄,因此,如何拓宽微穿孔板的吸声频带成为了微穿孔板相关研究的热点之一。国内外研究人员曾尝试用各种方法拓宽微穿孔板的吸声频带,如将微穿孔板的后空腔改为非常规形态[4-5]或用赫姆赫兹共振器代替[6],将微孔的形态改为圆锥形[7]等,这些非典型的微穿孔板结构均有良好的吸声效果。然而,文献[4-6]中改变后空腔并不是改变微穿孔板结构本身,也常常受到实际安装环境的限制。将微孔改为圆锥形则增加了微穿孔板的加工难度和加工成本。Chin等[8]用kenaf fiber and polylactic acid制成了复合材料微穿孔板,但其加工方法仍是传统的混合、打孔、热处理等,因此未能降低微穿孔板的加工难度和成本。
马大猷院士[2]提出的微穿孔板吸声结构经典理论可以用来准确模拟典型微穿孔板的声学特性,也可以用来针对特定频率设计微穿孔板。然而,对于非典型的微穿孔板结构,需要新的理论模型或其他仿真方法。Herdtle等[7]提出了圆锥孔微穿孔板的理论模型。Li等[9]提出了考虑薄膜振动边界条件对微穿孔薄膜声阻抗影响的理论,但未涉及微穿孔板的结构。Temiz等[10]研究了非均匀分布的微穿孔在考虑板振动情况下的声阻抗,然而也未涉及微穿孔板的结构。然而对于更复杂的非典型微穿孔结构,理论模型的建立更加困难。因此,有限元分析(Finite element analysis,FEA)成为对非典型微穿孔结构进行研究的新方法之一。Bolton等[11]用计算流体力学(Computational fluid dynamics,CFD)算法研究了典型微穿孔板的末端修正。Carbajo等[12]则证明了含有黏滞效应的FEA算法可以用来对微穿孔板进行声学仿真。
本文用有限元算法建立了典型微穿孔板和穿入不同数量金属纤维的微穿孔板模型,研究了两种微穿孔板的吸声系数、声阻抗和微孔内法向质点速度的空间分布,并进行了试验验证。用微孔体积减去穿入纤维体积求得的等效孔径和等效穿孔率代入经典微穿孔板理论求得了穿入纤维的微穿孔板吸声系数理论值,发现理论值与试验结果有较大差异。这证明由于穿入纤维的结构较为复杂,穿入纤维引起的黏滞声学效应也较为复杂,有必要使用有限元模型对穿入纤维的微穿孔板进行仿真。有限元仿真和试验数据表明,穿入金属纤维可以拓宽微穿孔板的吸声频带,但吸声系数也随之下降。本文第1节详细描述了两种有限元模型的建模方法,并用典型微穿孔板吸声系数的试验结果、理论解和仿真结果进行对比,验证了有限元模型的有效性;第2节是试验样品的制备与吸声系数的测量;第3节先用穿入纤维前后微穿孔板的吸声系数试验结果和仿真结果的对比验证了穿入纤维的微穿孔板有限元模型的有效性,然后用声阻抗和微孔内法向质点速度的空间分布分析了穿入纤维对微穿孔板声学性能的影响。研究结果表明,考虑黏滞效应的有限元模型可以有效模拟穿入纤维前后微穿孔板的声学特性,有限元仿真方法适用于结构相对复杂的微穿孔结构的声学建模,能直观地体现微孔复杂结构的影响,值得继续深入研究和工程应用。
1 穿纤维微穿孔板的有限元法建模
1.1 穿纤维微穿孔板及经典微穿孔板的有限元模型
为研究穿纤维微穿孔板的有限元建模,本文对典型的微穿孔板进行有限元仿真,并研究了穿入纤维后该微穿孔板的有限元模型。微穿孔板及穿入纤维的材料、结构参数如表1所示。穿入纤维的根数从0根(空白对照组,即经典的无纤维微穿孔板结构)、3根、7根增加到11根。
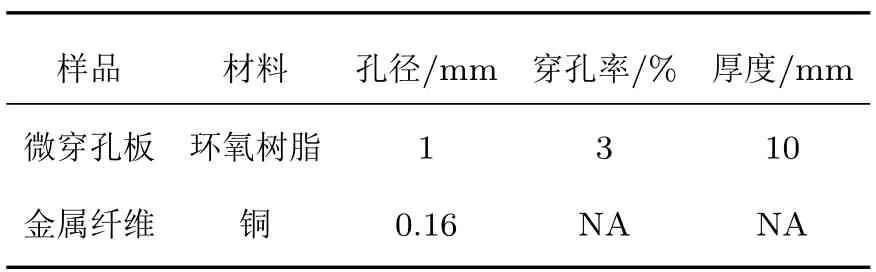
表1 微穿孔板及穿入纤维的结构参数Table1 Structural parameters of the MPPs and the inserted fibers
由于微穿孔板的吸声性能主要受微孔中的边界层黏滞效应影响,本文选用Comsol软件中的thermoacoustics模块对微穿孔板和穿入纤维的微穿孔板进行仿真。仿真频率为100~1600 Hz,此频率上限是由验证试验中使用的阻抗管决定的,详见2.2节。由于微穿孔板及穿入纤维的微穿孔板都是规则的圆孔结构,本文使用的有限元模型都是1/4对称模型,以加速计算过程。有限元模型的截面图如图1和图2所示。图1是微穿孔板及穿入纤维的微穿孔板的微孔有限元模型。图2是该微孔两端与外界空气连接部分的有限元模型示意图,外界空气层的尺寸是孔径的两倍,这保证了仿真模型的准确性。如图1和图2所示,本文的有限元仿真模型中,仅考虑穿入的金属纤维的空间占位和纤维边界的黏滞效应,金属纤维在流体中的振动、金属纤维与周围声场的声能热能交换均未考虑。
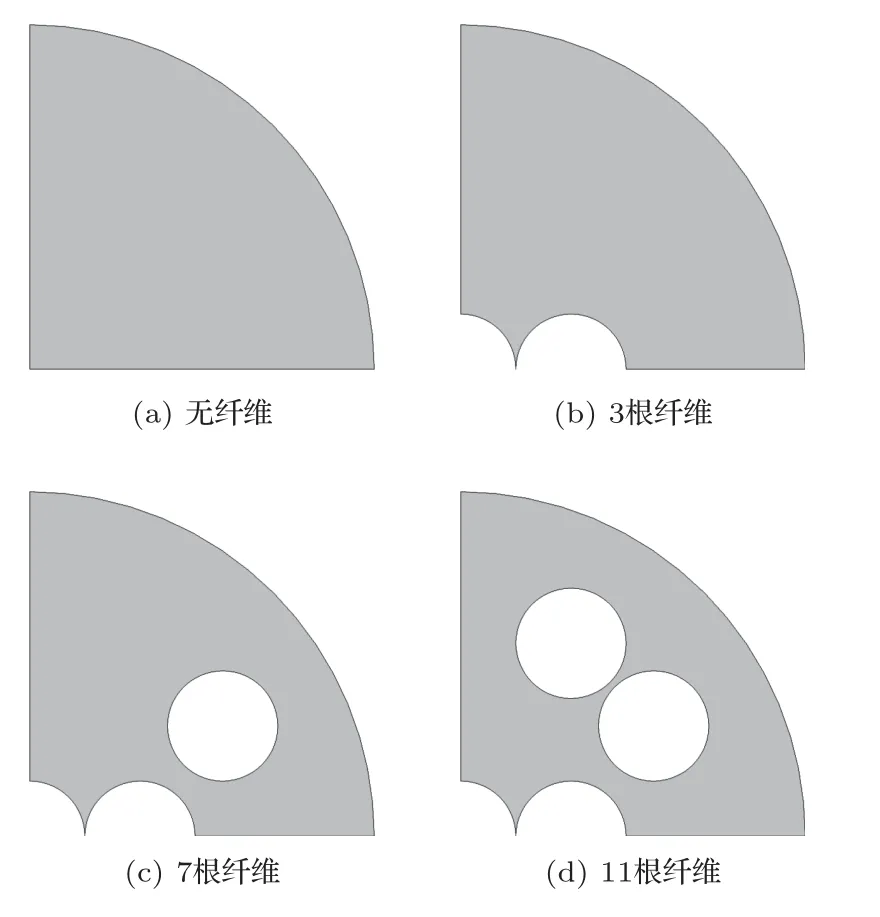
图1 微穿孔板及穿入纤维的微穿孔板的有限元模型Fig.1 FEA models of a perforation of the MPP without and with metal fibers
图3显示了穿入3根纤维的微穿孔板的1/4有限元完整模型。在微孔两端的空气层两端,使用perfectly match layer边界完全吸收层吸收平面波。在微孔某一端的空气层中设置平面波法向入射声源,以此在声场中形成法向入射的平面波声场。为保证仿真程序能较好地模拟微孔中边界层的黏滞效应对声场的影响,本文中微孔部分的网格尺寸较小,最大网格尺寸为1600 Hz时边界层厚度的1/3。仿真完成后,提取微孔一端的声压和法向质点速度即可得到微穿孔板的声阻抗,从而可以计算出微穿孔板的吸声系数。
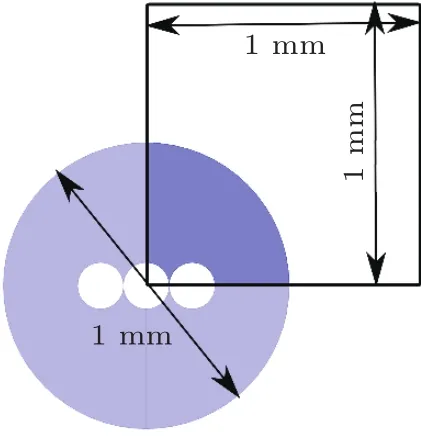
图2 穿入3根纤维的微穿孔板的1/4有限元模型,微孔部分Fig.2 A quarter FEA model of the MPP with 3 metal fibers,perforation only

图3 穿入3根纤维的微穿孔板的1/4有限元模型,完整模型Fig.3 A quarter FEA model of the MPP with 3 metal fibers,full model
1.2 经典微穿孔板的模型验证
为验证本文提出的有限元模型,选择无纤维的经典微穿孔板结构进行仿真,并将仿真结果与试验结果和理论值进行对比,如图4所示。微穿孔板的制备和试验过程的详细描述在第2节。由图4可以看出,理论结果与试验结果在共振频率以下吻合度较好,共振频率以上实验结果略高于理论结果,仿真结果的共振峰偏向低频20 Hz,但三条吸声曲线峰值和趋势均一致。因此可以认为仿真模型能较好地模拟微穿孔板的吸声特性,可以用该模型对穿纤维的微穿孔板进行有限元仿真。
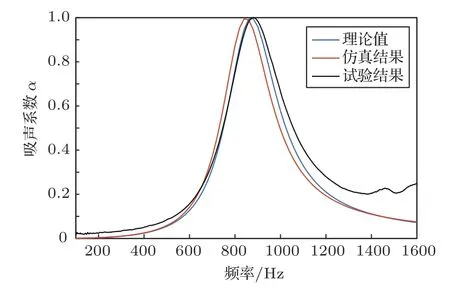
图4 理论、仿真和试验得到的无纤维微穿孔板的吸声系数,后空腔深度为10 mmFig.4 Comparation of the sound absorption coefficients obtained by the classic theory,the proposed simulation,and the measurement,the depth of the backing cavity is 10 mm
2 穿纤维微穿孔板有限元模型的试验验证
2.1 穿纤维微穿孔板的制备
为验证本文提出的有限元模型,本文制备了穿入铜纤维的微穿孔板。微穿孔板由环氧树脂制成,按表1所示的结构参数用台钻穿孔。穿入的铜纤维如图5所示,其材料参数如表1所示。图6是穿入11根铜纤维后的微穿孔板。

图5 穿入微穿孔板的铜纤维Fig.5 The copper fibers inserted into the MPP

图6 穿入铜纤维后的微穿孔板,穿入纤维数量为11根Fig.6 The MPP with 11 copper fibers inserted
2.2 穿纤维微穿孔板的吸声系数试验
本文用阻抗管法进行吸声系数试验,如图7所示。本文使用的是B&K公司的4206型阻抗管及其适配的传声器、功率放大器,信号采集系统为Pulse 3560C系统,并用白噪音信号进行激励。
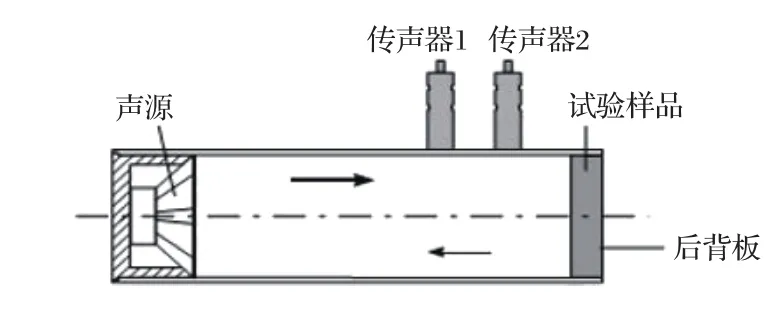
图7 阻抗管法测吸声系数示意图Fig.7 The measurement of the sound absorption coefficient using the impedance tube with two microphones
微穿孔板远离声源端附加一个10 mm厚的空气层作为后空腔。测试过程中采集两个传声器之间的传递函数,以此计算出微穿孔板和后空腔组合结构的吸声系数。后空腔的影响未在有限元仿真模型中模拟,但可以用仿真得到的声阻抗加上后空腔的声阻抗来模拟含后空腔的微穿孔板声阻抗,从而得到含后空腔的微穿孔板吸声系数。考虑到实际测量重复装配过程中后空腔厚度的误差以及穿入金属纤维后金属纤维厚度对后空腔的影响,本文中计算中的后空腔厚度允许±2 mm误差。
3 穿纤维微穿孔板吸声系数试验结果与仿真结果的对比
3.1 穿入纤维对微穿孔板吸声系数的影响
本文对比了微穿孔板穿入3根、7根、11根金属纤维前后吸声系数的仿真结果和试验结果,分别如图8和图9所示。仿真结果和试验结果均含有后空腔影响,后空腔厚度如2.2节所述。图8中的吸声系数仿真结果显示,随着穿入纤维数量的增加,吸声系数的峰值降低,吸声系数峰值出现的频率向低频移动。图9的试验结果显示相同的峰值降低、频率向低频移动的趋势。图10为用微孔体积减去穿入纤维体积求得的等效孔径和等效穿孔率代入经典微穿孔板理论求得的穿入纤维的微穿孔板吸声系数理论值,与试验结果有较大差异,证明了使用有限元模型对穿入纤维的微穿孔板进行仿真的必要性。由此可见,本文提出的有限元模型可以有效模拟穿入纤维前后微穿孔板的声学特性。

图8 典型微穿孔板与穿纤维微穿孔板吸声系数的仿真结果Fig.8 Simulation results of the sound absorption coefficients of the classic MPP and the MPP with copper fibers
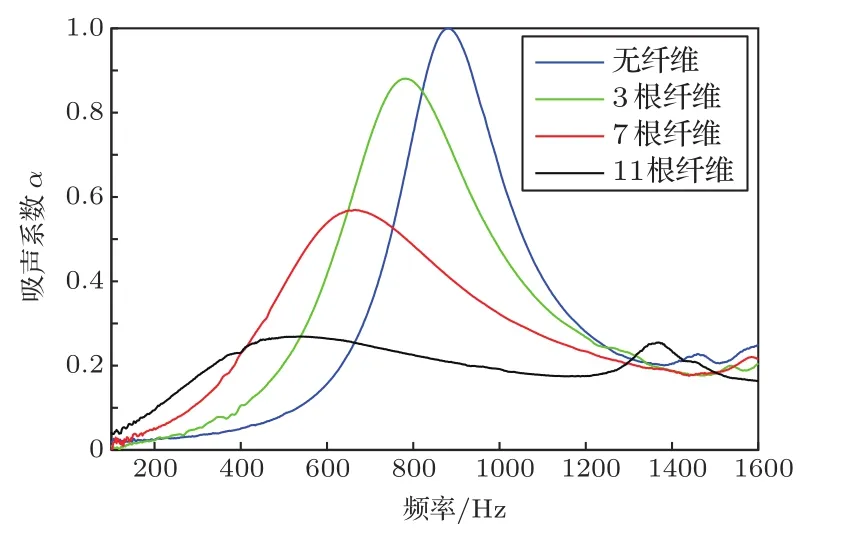
图9 典型微穿孔板与穿纤维微穿孔板吸声系数的试验结果Fig.9 Experimental results of the sound absorption coefficients of the classic MPP and the MPP with copper fibers

图10 典型微穿孔板与穿纤维微穿孔板吸声系数的理论结果,使用等效孔径和等效穿孔率Fig.10 Analytical results of the sound absorption coefficients of the classic MPP and the MPP with copper fibers,using the equivalent diameter and the equivalent perforation ratio
对比图8和图9可以发现,尽管仿真结果和试验结果显示出相同的趋势,穿纤维微穿孔板的吸声系数仿真结果在共振频率上普遍低于相应的试验结果,而在1000 Hz以上则普遍略高于试验结果。这些仿真结果和试验结果之间的差异可能由以下原因引起:(1)如1.1节所述,本文的有限元仿真模型中,仅考虑穿入的金属纤维的空间占位和纤维边界的黏滞效应,金属纤维在流体中的振动、金属纤维与周围声场的声能热能交换均未考虑,而这些被有限元模型忽略的因素都可能引起有限元仿真的误差;(2)对比图1和图6发现,试验样品中的金属纤维是连续穿入的,因此在微孔两端存在横向的金属纤维,这些横向的金属纤维会影响入射声场的变化,也会产生微孔表面的黏滞效应,而这些都未在有限元模型中体现,因此可能造成了误差。综上所述,尽管有限元仿真中忽略了一些因素造成了一定的误差,有限元仿真可以有效模拟穿入纤维前后微穿孔板的声学特性,为穿纤维微穿孔板的声学性能研究提供了便利和新的研究方法,值得继续研究。
3.2 穿入纤维对微穿孔板声阻抗的影响
如3.1节所述,图8中的吸声系数仿真结果显示,随着穿入纤维数量的增加,吸声系数的峰值降低,吸声系数峰值出现的频率向低频移动,而图9的试验结果证明了这一趋势实际存在。由于仿真和试验中均使用相同的微穿孔板,可以认为穿入的纤维是引起这一趋势变化的唯一因素。因此可以推测,穿入金属纤维导致微孔内的黏滞效应增加,声阻增加,而高声阻会引起吸声系数的降低[13]。
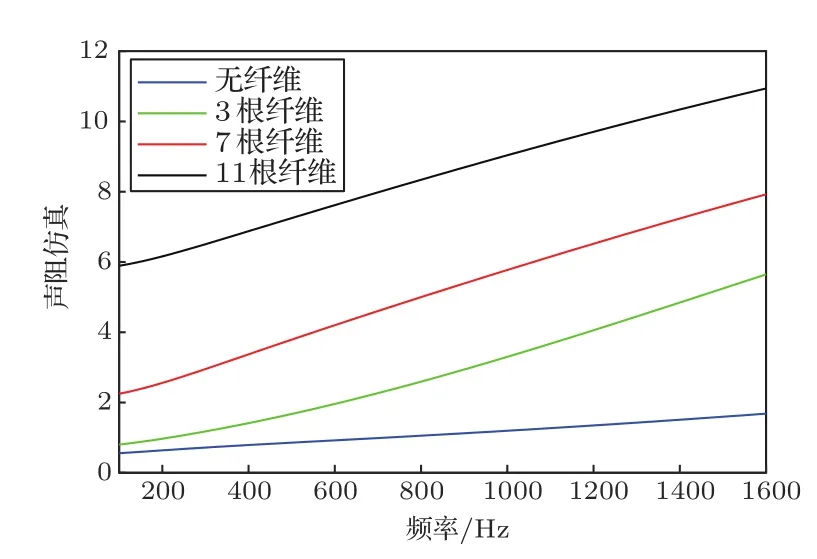
图11 典型微穿孔板与穿纤维微穿孔板有限元仿真的声阻Fig.11 Simulated resistance of the MPP without and with 3,7,and 11 metal fibers
图11是典型微穿孔板与穿纤维微穿孔板声阻的仿真结果。由图11可以看出,随着穿入纤维数量的增加,声阻仿真结果在仿真频带内呈增加趋势。这证明了穿入金属纤维导致微孔内的黏滞效应增加、声阻增加、吸声系数降低的推测。图12是典型微穿孔板与穿纤维微穿孔板声抗的仿真结果,其中均未考虑后空腔对声抗的影响。由图12可以看出,随着穿入纤维数量的增加,声抗的仿真数据在低于700 Hz的频带内差别不大,而在700 Hz以上频率随着穿入纤维的增加而稍有降低。图12 典型微穿孔板与穿纤维微穿孔板有限元仿真的声抗(无后空腔影响)
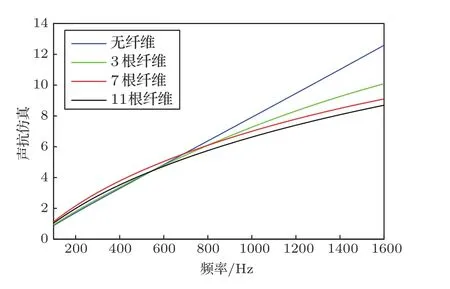
图12 典型微穿孔板与穿纤维微穿孔板有限元仿真的声抗(无后空腔影响)Fig.12 Simulated reactance of the MPP without and with 3,7,and 11 metal fibers(without the effect of the back cavity)
3.3 穿入纤维对微穿孔内边界层的影响
从微穿孔板经典理论可知,微穿孔板的吸声主要是由微孔内质点速度的黏滞效应引起的,主要与微穿孔内的质点速度分布和边界层有关[2-3]。为了进一步分析穿入纤维对微穿孔板声学特性的影响,本文绘制了200 Hz和600 Hz时微孔内的法向质点速度云图,分别如图13和图14所示。
由图13和图14可以发现,对无纤维的典型微穿孔板而言,在200 Hz和600 Hz时法向质点速度分布都是微孔中心较高,微孔边界为0,符合微穿孔板理论[2-3]。穿入3根纤维时,从200 Hz和600 Hz时法向质点速度分布云图上可以明显看到微孔边界上的黏滞效应导致的低速区域,但纤维导致的黏滞效应并不明显。这是由于如图1和图2所示,本文使用的有限元模型假设3根纤维在微孔正中心位置,而该位置的法向质点速度较高,使纤维的黏滞效应很难体现,纤维引起的边界层太薄以至于无法显示出来。穿入7根和11根纤维后,可以明显看到在1/4模型中间部位的纤维边界上出现了低速区域,而且该低速区域可与微孔边界上原本存在的低速区域连起来,形成较大的低速区域。这些现象体现了穿入纤维对微穿孔板黏滞效应和边界层的影响,符合吸声系数和声阻抗分析的趋势。
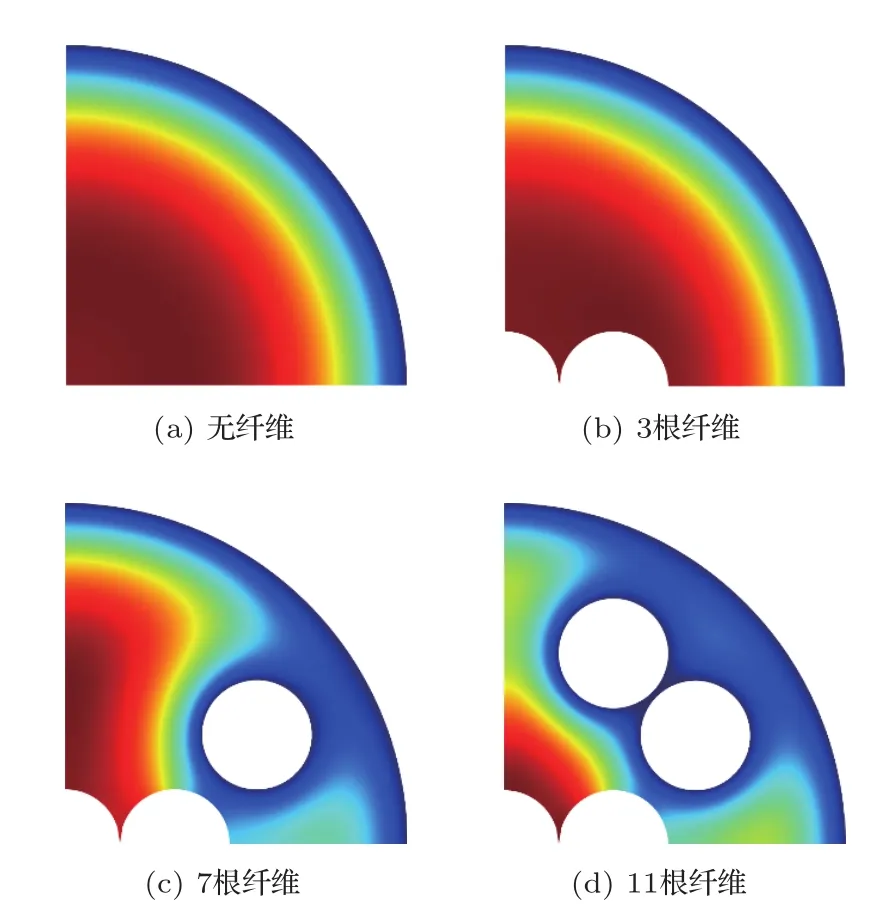
图13 200 Hz微穿孔板及穿入纤维的微穿孔板的法向质点速度仿真结果Fig.13 The simulated results of the particle velocity in the perforation at 200 Hz
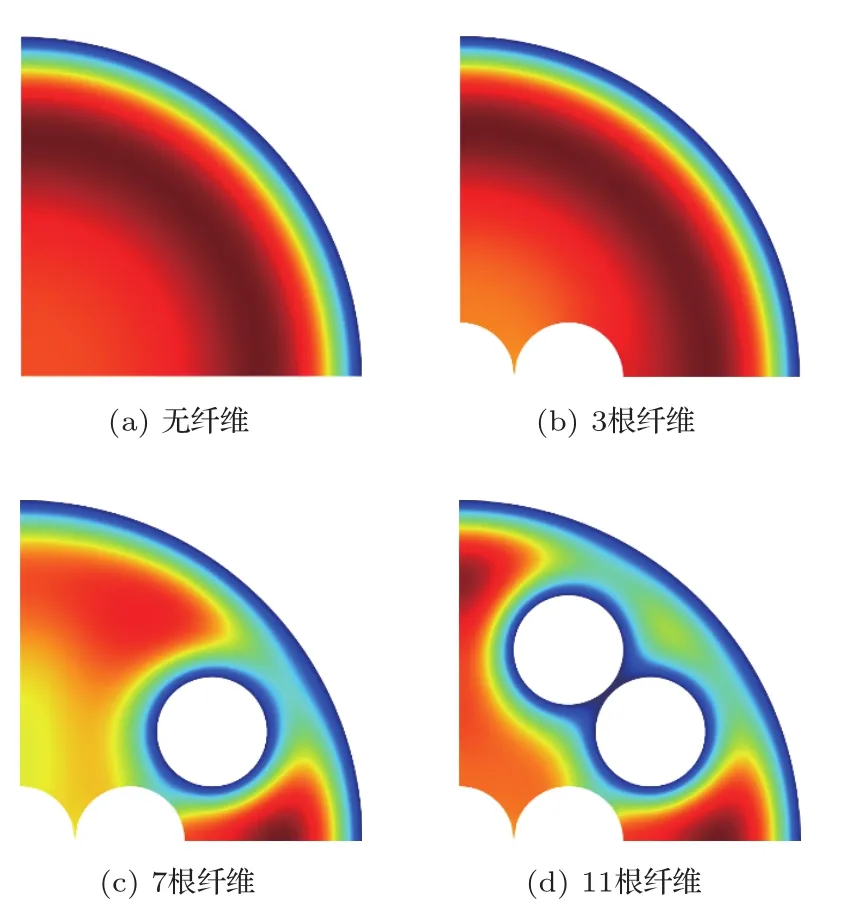
图14 600 Hz微穿孔板及穿入纤维的微穿孔板的法向质点速度仿真结果Fig.14 The simulated results of the particle velocity in the perforation at 600 Hz
4 结论
本文利用有限元建模方法研究了穿纤维微穿孔板的吸声特性、声阻抗以及微孔内的黏滞效应,并用试验验证了有限元模型的仿真效果。主要结论如下;
(1)吸声系数仿真结果与试验结果趋势一致,存在误差主要是因为现有仿真模型忽略了金属纤维在流体中的振动、金属纤维与周围声场的声能热能交换、试验样品与几何模型之间的差异等因素;
(2)对声阻抗的仿真结果表明,穿入金属纤维导致微孔内的黏滞效应增加,声阻增加,而高声阻会引起吸声系数的降低,而声抗变化不大;
(3)分析法向质点速度分布云图发现,随着穿入金属纤维数量的增加,黏滞效应引起的低质点速度区域增大,这符合吸声系数和声阻抗分析的趋势。
试验结果及微穿孔板吸声原理表明,考虑黏滞效应的有限元模型可以有效模拟穿入纤维前后微穿孔板的声学特性,证明有限元仿真方法适用于典型微穿孔板和穿纤维微穿孔板的声学研究。因此,有限元仿真方法适用于结构相对复杂的微穿孔结构的声学建模,仿真结果有效,能直观地体现微孔复杂结构的影响,值得在微穿孔板相关研究中继续深入研究和应用。
