基于改进EKF算法的动力锂电池SOC估算技术研究

蒋 聪，吴 斌，王顺利，熊 鑫

(西南科技大学信息工程学院，四川 绵阳 621010)

0 引言

近年来，随着锂电池内部正负极、隔膜和电解液等材料的不断优化改进，工作性能高速发展，使得锂电池大量运用在新能源汽车、航空、分布式储能等领域。而锂电池荷电状态(state of charge，SOC)的准确估算是锂电池组安全高效工作的重要参数[1]，是判断电池管理系统(battery management system，BMS)优劣的关键依据。但因为动力锂电池所具有很强的非线性特征，以及外部复杂环境和使用工况的影响，如温度、放电倍率等，在实际应用中仍然难以保证算法的可靠性和对SOC估计精度，最终将降低电池管理系统的工作效率和安全性。本文提出一种基于改进扩展卡尔曼的SOC估算算法，可以有效防止因计算机字长度有限而引起的滤波发散。

1 等效模型构建

1.1 理论分析

电池等效电路模型图如图1所示。

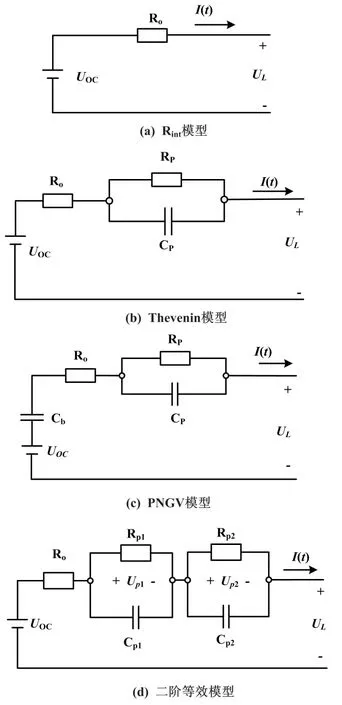
图1 电池等效电路模型

一般电池模型分为电化学模型、等效电路模型、纯数学模型，由于等效电路模型具有结构简单、物理意义明确的特点，在研究中使用较为广泛。常用等效电路模型有Rint模型、Thevenin模型、PNGV模型和二阶等效模型。

在Rint模型中：R0为锂电池的欧姆内阻，表征锂电池电流突变引起的瞬时压降；UOC为理想电压源表征开路电压；I为电池的环路电流，设定其放电方向为正；UL为锂电池负载端电压。在Rint模型基础上添加1个RC并联回路表征电池的极化效应，分别为极化内阻Rp、极化电容Cp，模拟电池充放电过程中的电压缓慢变化，得到了Thevenin模型。在Thevenin模型上添加Cb，表征负载电流随时间产生的开路电压变化，得到了PNGV模型。在Thevenin模型上再添加一个RC并联回路，得到了二阶等效模型。

简单的模型便于计算，但不能准确地描述电池的工作特性，复杂的模型能更好地表征电池的充放电特性，但计算量会大大增加，降低了模型的适应性和推广应用。Lai等比较了不同阶数等效电路模型对于SOC估算效果的影响[2-5]，其中二阶以上，模型精度增加并不明显，但计算量大大增加。综合考虑精确建模和模型简约，本文采用二阶等效电路模型。根据基尔霍夫(Kirchhoff)电路定律，结合图1(d)，可以列出式(1)。

(1)

式中:UL为负载端电压；Uoc(SOC)为开路电压；i为负载电流；RO为欧姆内阻；UP1、UP2为两个极化电容端电压；CP1、CP2为极化电容；t为时间。

针对所选取的二阶等效模型，选取[SOCUP1UP2]作为状态变量，结合式(1)及SOC的定义，经过离散化可以列出锂电池离散状态空间方程如式(2)所示。

(2)

式中:下标k为当前时刻，k+1代表下一时刻；Qn为电池额定电量；SOC为电池荷电状态，当前电量和电池额定电量的比值；h为库伦效率；T为采样周期；RO为欧姆内阻；Rp1、Rp2为极化内阻；UP1、UP2为两个极化电容端电压；t1、t2为时间常数，t1=Rp1Cp1、t2=Rp2Cp2；UL为负载端电压；Uoc为开路电压。

二阶等效电路模型所需要辨识的参数有欧姆内阻RO、开路电压Uoc、极化内阻Rp1、Rp2和极化电容Cp1、Cp2。这里选择对动力锂电池进行混合脉冲功率性能(hybridge pulse power characteristic，HPPC)测试试验，根据锂电池外部特性变化，运用Matlab软件根据最小二乘原理进行离线参数辨识。

1.2 HPPC试验

以中航锂电三元锂电池LFP50AH为研究对象，电池测试设备为亚科源BTS750-200-100-4，参考《美国Freedom CAR电池试验手册》对锂电池进行HPPC试验。单次HPPC试验工步过程为：以放电倍率1 C(这里电流为50 A)恒流放电10 s、搁置40 s、以放电倍率1 C(这里电流为50 A)恒流充电10 s、再搁置。HPPC试验电流电压曲线如图2所示。

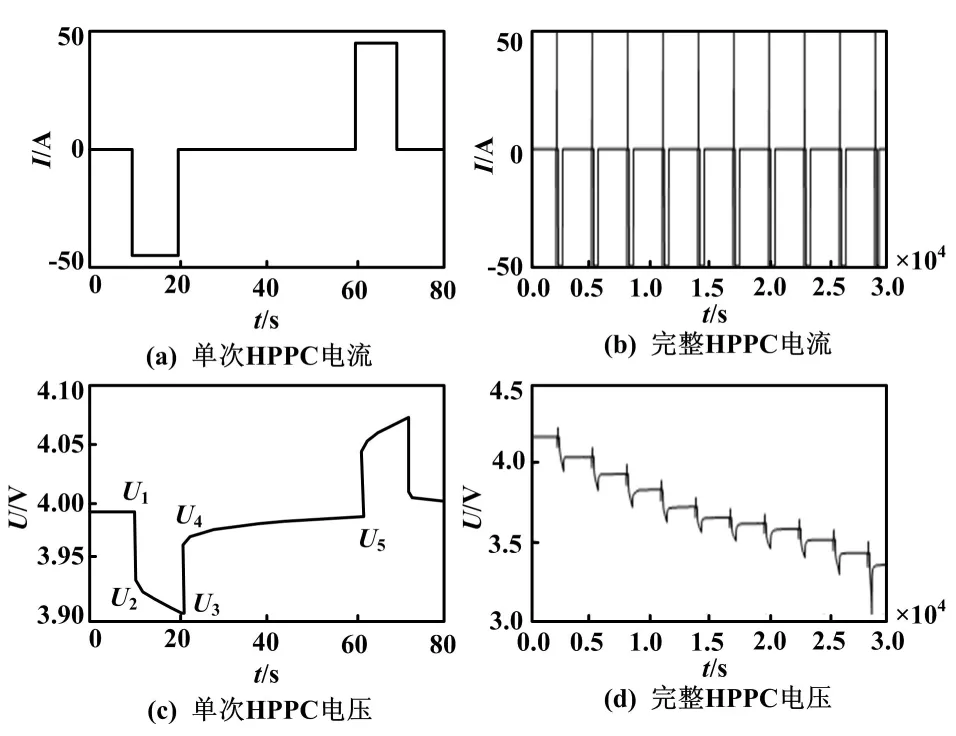
图2 HPPC试验电流电压曲线图

分析图2，可以得到以下4个阶段特点。

①t1时刻开始放电。锂电池端电压从U1突降变为U2。这主要是由于锂电池欧姆内阻引起的电压变化。

②从t2到t3期间，锂电池端电压从U2缓慢下降到U3。这是由于电池极化效应存在，放电电流对极化电容充电的过程，是双RC串联回路的零状态响应。

③从t3到t4期间，锂电池端电压从U3突升变为U4。这同样是由于锂电池欧姆内阻引起的电压变化。

④从t4到t5期间，锂电池端电压从U4缓慢回升到U5。这是极化电容对极化电阻放电的过程，是双RC电路的零输入响应。

1.3 模型参数辨识

1.3.1 开路电压

开路电压UOC是电池在长时间静置状态下电池正负两端稳定的电压。试验表明，将电池静置40 min后的电压稳定，可以认为等于电池的开路电压。故可以取图2(a)中U1为该SOC值下对应的开路电压。通过上述HPPC试验，可以直接读出SOC值0.1～1对应的10个开路电压值。

1.3.2 欧姆内阻

由特征可知，锂电池在放电瞬间以及停止瞬间端电压会突变，均是由于欧姆内阻导致的。故可以选取两电压差求均值除以电流得到欧姆电阻，如式(3)所示。

(3)

式中：U1为图2(c)中开始放电时锂电池端电压；U2为图2(c)中U1突降后端电压；U3为图2(c)中放电10 s结束时端电压；U4为图2(c)中U3电压突升后端电压；I为放电电流，其值为50 A。

1.3.3 极化电容极化电阻

从图2(a)特征可以看出，从t2到t3期间，锂电池端电压从U2缓慢下降到U3。这是由于电池极化效应存在，放电电流对极化电容充电的过程是双RC回路串联的零状态响应。对电路进行时域分析，选取t2到t3期间数据，可以得到一个端电压UL与时间t的函数关系，如式(4)所示。

UL(t)=U2-IRP1[1-e-t/τ1]-IRP2[1-exp-t/τ2]

(4)

式中：UL(t)为负载端电压；t为时间，从U2为0时刻开始计时。

将极化内阻Rp1、Rp2以及t1、t2作为未知量，根据公式(4)和从t2到t3期间的数据。运用Matlab中的cftool拟合工具，可以直接得到4个值，再根据公式t1=Rp1Cp1、t2=Rp2Cp2，求出极化电容Cp1、Cp2。

2 SOC估算算法

电池的SOC估算是一个明显的隐马尔科夫模型，针对传统SOC估算方法对初值的依赖以及算法的稳定性，提出一种在扩展卡尔曼算法基础上，将状态协方差矩阵进行平方根分解得到的扩展卡尔曼滤波(extended Kalman filter,EKF)算法，具有SOC初值自适应修正能力，也有效防止因为计算机字长有限而可能引起的滤波发散。

卡尔曼滤波主要步骤是设定状态向量初值X(0|0)及其协方差矩阵初值P(0|0)，根据模型计算下一时刻估计值，再计算卡尔曼增益，通过卡尔曼增益修正估计值。在实际运用中，有时出现滤波发散问题。这可能是由于计算机的舍入误差(计算误差)，使得P(k|k-1)、P(k|k)的计算值失去非负定性，导致K(k)的计算失真，造成误差越来越大。对于矩阵S，可得SST是对称非负定的。

锂电池SOC估算流程如图3所示。

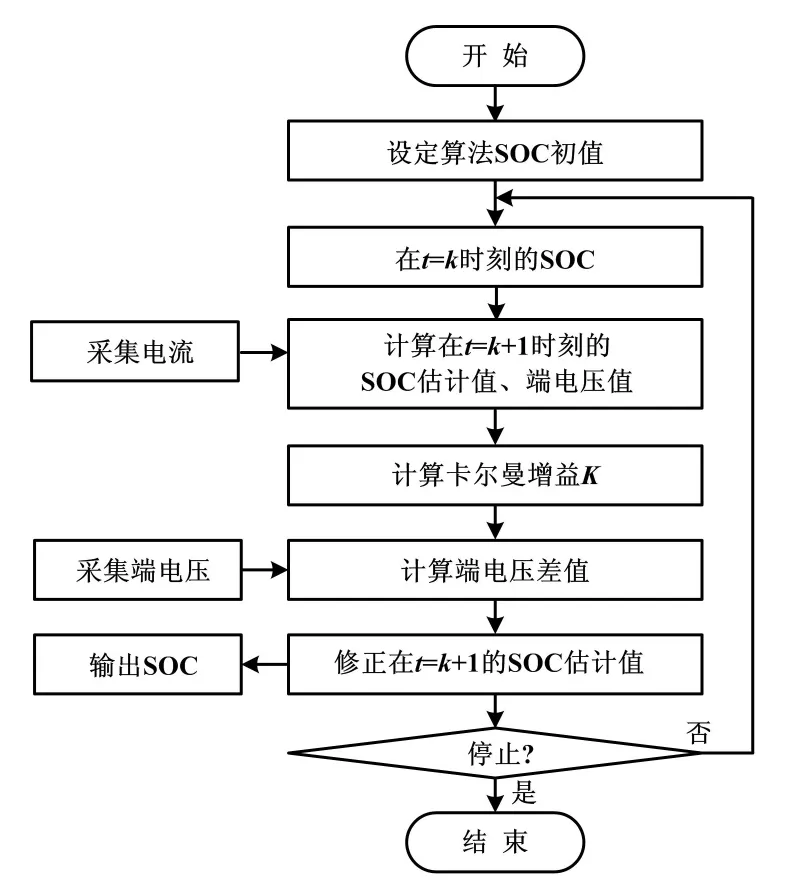
图3 锂电池SOC估算流程图

因此，可将状态协方差矩阵P(k|k)进行分解为S(k|k)S(k|k))T，任何时刻至少具有非负定性。矩阵的分解方法如式(5)和式(6)所示。

(5)

(6)

式中：Pnn为协方差矩阵中第n行n列的值；Snn为分解协方差矩阵中第n行n列的值。

根据式(5)、式(6)，对协方差矩阵P进行矩阵分解，故此可以得到相应的改进扩展卡尔曼算法。首先是设定算法初值X(0|0)、S(0|0)。然后进入时间更新预测阶段，根据状态空间模型从(k-1)时刻的最优预测值X(k-1|k-1)根据式(2)直接计算出的k时刻预测值X(k|k-1)及其对应状态变量协方差矩阵P(k|k-1)的分解矩阵S(k|k-1)，改进的扩展卡尔曼算法计算过程预测阶段式(7)和式(8)所示。

X(k|k-1)=A(k)X(k-1|(k-1)+BIk

(7)

S(k|k-1)=A(k)S(k-1|k-1)

(8)

式中：X(k|k-1)为根据公式从(k-1)时刻计算得到k时刻系统状态；X(k-1|k-1)为(k-1)时刻观测更新修正后的系统状态；A(k)为状态转移矩阵；B为控制矩阵；S(k|k-1)为从(k-1)时刻计算得到k时刻协方差分解矩阵；S(k-1|k-1)为(k-1)时刻观测更新修正后协方差分解矩阵。

接着观测更新修正阶段，通过计算卡尔曼增益K(k),如式(9)所示。再对直接计算出的k时刻预测值X(k|k-1)及协方差分解矩阵S(k|k-1)进行修正，得到了最优估计值X(k|k)。计算过程如式(10)和式(11)所示。

(9)

X(k|k)=X(k|k-1)+K(k)[UL(k)-H(k)×

(k|k-1)-BI(k)]

(10)

(11)

式中：K(k)为卡尔曼增益；Fk、αk、γk为使公式简洁的中间量；R为观测白噪声的方差；H(k)为观测矩阵；X(k|k)为k时刻观测更新修正后的系统状态；H(k)为状态转移矩阵；S(k|k)为k时刻观测更新修正后协方差分解矩阵。

在给定初值X(0|0)、S(0|0)的情况下，通过以上公式进行迭代，就可以得到每个时刻状态向量X(k|k)。根据所选取的状态向量为[SOCUP1UP2]T,输出估计状态量的第一项即为需要的SOC估计值。根据以上算法进行SOC估算，因为P(0|0)非负定，至少应保证状态协方差矩阵P(k|k)总是非负定的，从而克服因计算机字长有限而可能引起的滤波发散。

3 试验验证

3.1 BBDST工况

本文参考北京公交动态测试(Beijing bus dynamic stress test，BBDST)工况，设置工况试验，对所用中航锂电LFP50AH三元锂电池进行测试。电池充放电设备是由深圳市亚科源科技有限公司提供的BTS750-200-100- 4电池检测设备，BBDST工况是对北京公交车起步、加速、滑行、制动、急加速、停车等各个环节的数据采集后进行处理所得到工况。由于本文是对锂电池单体进行研究，根据实际情况，将每步工况功率按比例缩小。BBDST工况描述如表1所示。

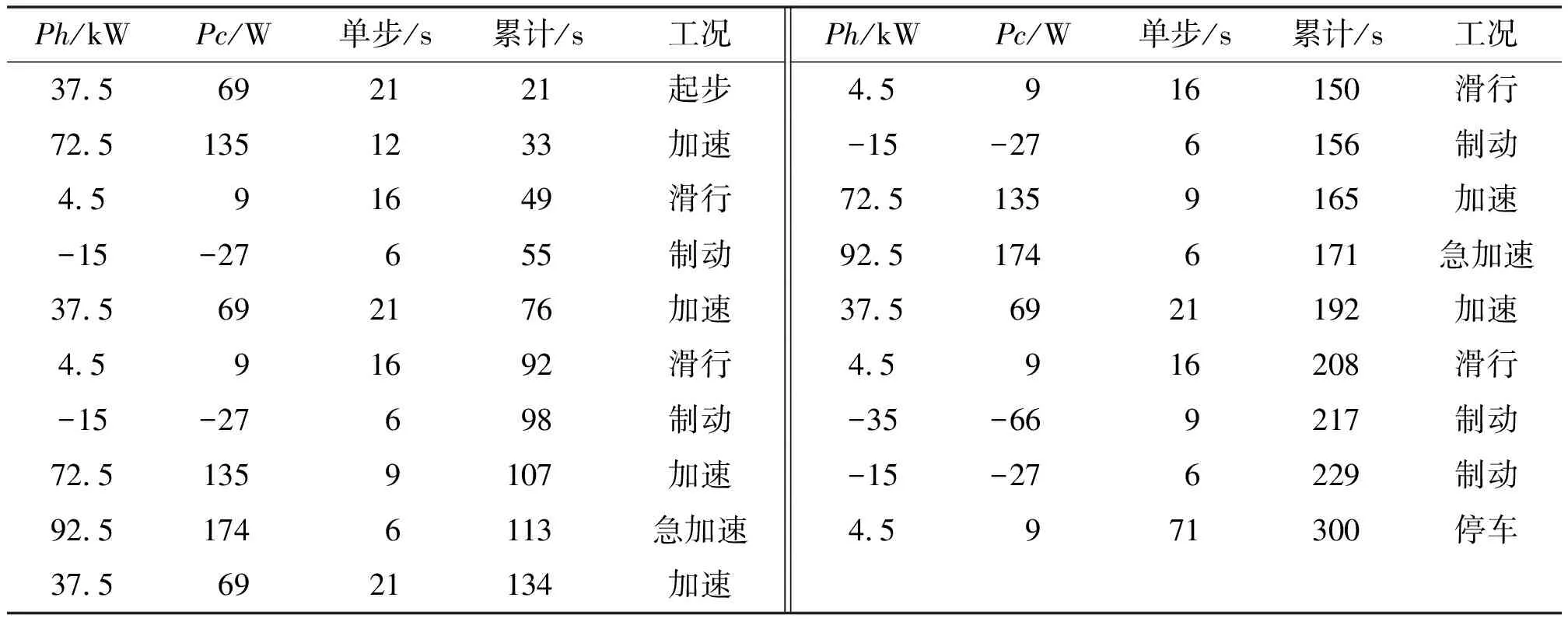
表1 BBDST工况描述

表1中:Ph为真实的公交车起步加速滑行等工况下电池输出功率。由于是对50 Ah锂电池单体进行试验，对Ph进行减小，得到了Pc中数据。Pc为本次对中航锂电LFP50AH三元锂电池进行试验所用工况数据。单步为每一步工况时长，累计为工况累计时长。从表1可知，一次完整BBDST工况时长300 s。这里对电池进行20次BBDST工况测试。BBDST工况试验数据如图4所示。

图4 BBDST工况试验数据

随着循环次数增加，放电电流增大，电池端电压整体呈现下降趋势

3.2 仿真结果与分析

选择在Matlab/Simulink中建立仿真系统模型，用于验证算法SOC估算效果。结合根据前面知识，如所获得二阶等效电路模型参数数据、BBDST试验数据，建立Simulink仿真模型[6-10]。

运行仿真后得到SOC估算结果如图5所示。

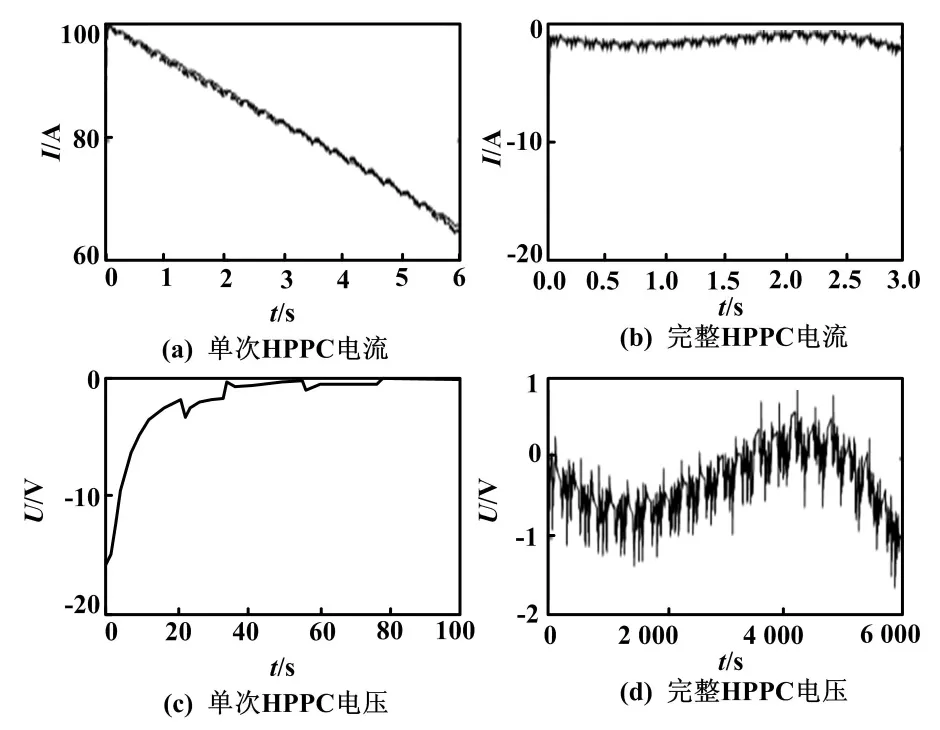
图5 SOC估算结果

从图5(a)所示的SOC估算图可知：20次BBDST工况试验，所用锂电池SOC从100%下降到65%，初始SOC误差为25%；改进EKF迭代10s后误差降低到10%，80 s后最大误差低于2%。对误差值取绝对值后，再取平均数，得到平均误差为0.45%。结果表明，算法估算效果良好，且具有很强的修正初值误差的能力。

4 结束语

对动力锂电池LFP50AH建立二阶等效电路模型，使用改进EKF算法进行SOC估算。在BBDST工况下，设定初始SOC误差为25%。仿真结果表明，锂电池SOC估算误差在10 s后低于10%，在80 s后最大误差低于2%，全程平均误差为0.45%。改进EKF算法能有效修正SOC初值引起的误差，并防止因为计算机字长有限而引起的滤波发散，且估算效果良好。