基于非迭代多点插值DFT的谐波电能计量算法

唐旭明，翁东波，宋雅楠，郝晶晶，张 明，李 冰

(1.国网淮南供电公司，安徽 淮南 232007；2.烟台东方威思顿电气有限公司，山东 烟台 264000)

0 引言

伴随国民经济快速发展的需求，现代化电气高速铁路、特高压输电等加快投入使用。一方面，这促进了固态开关器件、非线性电力电子开关负载、工业设备整流器和逆变器新型电力电子器件在电网系统中大量应用，使得系统控制、保护等更为准确、稳定。另一方面，非线性电力电子器件应用产生大量谐波(稳态或动态)[1-2]所带来的电能质量问题，不仅危及供电系统整体安全、稳定运行，而且直接影响电能计量的准确性，进而造成巨大的经济损失。因此，在这种情况下，精确谐波电能计量显得尤为必要和重要。这已成为电力公用事业及其客户的重要研究课题。

在非正弦含谐波情况下，谐波标准IEEE STD 1459[3]有功功率定义为：

(1)

式(1)表明，准确估计测量直流、基波及各次谐波参数(幅值、相位及频率)是确保谐波电能精确计量的前提。常用谐波估计算法分为时域和频域两大类。由于频域方法具有高精度和较低计算负担，在处理实时应用时它们通常比时域方法更受青睐。

插值离散傅里叶变换(interpolated discrete Fourier transform,IpDFT)是较广泛采用的频域方法。该类算法采用加窗和插值的方法，分别处理非相干采样引起的频谱泄漏，以及由频谱中离散频率引起的栅栏效应引起的估计不准确影响，并基于快速傅里叶变换(fast Fourier transform,FFT)使得算法实现简单且可用于实时处理。典型IpDFT算法有非参数插值(补零、线性调频和频率翘曲[3-4])和特定时间窗函数方法。其中，通过剖析频谱泄漏现象的本质，采用加余弦窗(包括多级卷积窗[5-6])的线性插值及多点谱线加权插值(multipoint weighted interpolated discrete fourier transform,MWIpDFT)方法是目前研究的重要方向[7-11]。该类方法通常分粗略估计和精细补偿校正两步实现。粗略估计通过基于频率估计器对采样信号使用加窗FFT(windowing FFT,WFFT)并搜索幅度谱全局最大值实现；精细补偿校正通常通过内插与最大谱线相邻谱线来实现，以补偿校正栅栏效应导致的偏移误差。

在插值补偿校正时，由于偏移补偿量与DFT谱线幅度谱的非线性关系通常采用多项式近似逼近，因而在一定程度上降低了补偿精度。文献[12]提出提升插值离散傅里叶变换(enhanced interpolated discrete Fourier transform,EIpDFT)算法。其核心在于采用迭代过程消除了与共轭分量及其他频次谐波对参数估计结果的影响，大幅度提高了频率校正及幅值相位估计精度。但迭代过程的高额计算成本使得其在实时计算应用存在困难。

因此，本文在EIpDFT算法的基础上，采用非迭代方式扩展应用基于任意阶最大衰减旁瓣窗(maximum decay sidelobe windows,MSDW)的多点插值方法，在短时间窗长内对多频谐波信号的基本正弦分量进行参数估计。最后，根据谐波标准IEEE STD 1459功率定义，将得到的谐波参数用于谐波电能准确计量。一方面，非迭代方式有效降低了每次参数估计的计算负担。另一方面，短时间窗截断使得该类算法还可应用于快速波动情况下电网信号谐波参数估计，扩大了IpDFT的应用范围。

1 通用加窗傅里叶变换

假设信号中仅含有单一频率分量，其离散时间采样表示为：

(2)

式中：An、fin和θin分别为信号幅值、频率和起始相位；fs、N为采样频率和采样点数。

实际情况下，考虑非同采样情况，信号频率可以表示为：

(3)

式中：Δf为N点采样下的频率分辨率；η为信号截断周期数；l(整数)为η的四舍五入值；τ∈[-0.5,0.5]为信号频率在离散谱线间的所处位置，即归一化情况的频率偏差。

对N点离散信号进行加窗w(n)傅里叶变换，得：

λ-η)ejθin+W(l+λ+η)e-jθin

(4)

式中：λ用于确定在插值中使用的多条谱线位置[13]；W()为窗函数的离散频谱表达式。

根据H阶最大衰减旁瓣余弦窗的定义：

(5)

对应权重系数分别为：

(6)

(7)

则当H>1、ζ=N及N>1时，H阶最大衰减旁瓣余弦窗的频谱表达式近似为：

(8)

根据式(8)，H≤6的窗函数系数及重要性能指标，包括主瓣宽度(MLBW)、旁瓣衰减速度(SLdec,单位dB/oct)及等效噪声带宽(ENBW)。最大衰减旁瓣余弦窗参数如表1所示。

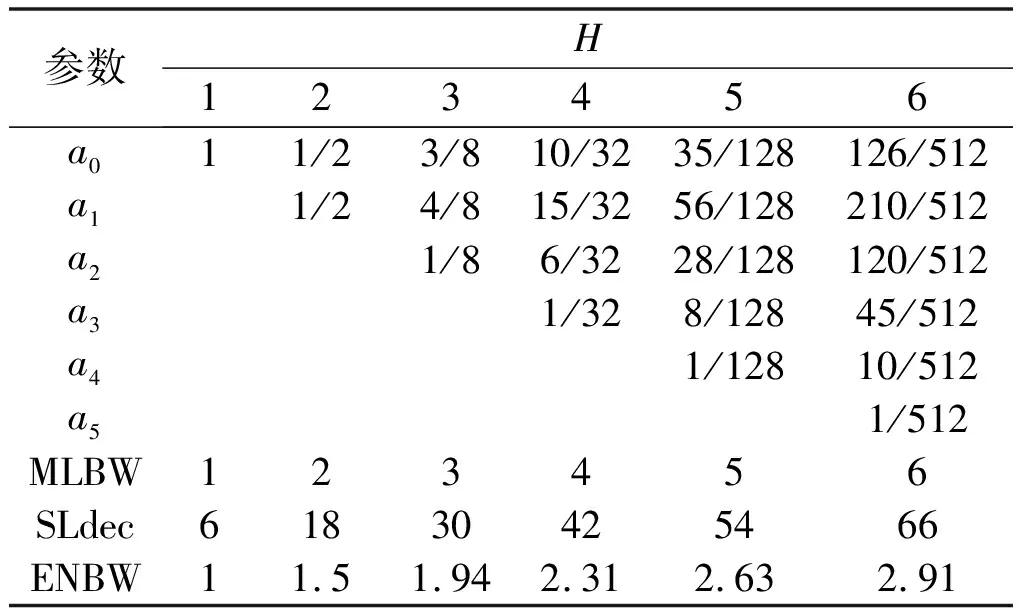
表1 最大衰减旁瓣余弦窗参数

2 插值校正

多点插值校正方法在前述加窗DFT基础上，通常分两步实现：粗略估计和精细补偿校正。以常用三谱线插值修正算法为例[15]。首先，利用局部峰值搜索(周期图)，在等间隔离散频谱上寻找实际峰值频率点附近最大谱线，将其作为粗略频率估计值。其次，联立峰值谱线左右两个次最大谱线幅值，采用非线性拟合方式得到频率修正系数，完成精细补偿校正过程(若需进一步计算幅值和相位，则可再次通过非线性拟合方式得到频率修正系数与幅值及相位的关系，将其代入得到幅值和相位的补偿校正)。

值得注意的有两点：①非线性拟合方式精度与其采用的计算方法有着直接的关系，同时也额外增加了计算成本；②在利用三谱线非线性拟合求频率修正的过程中，常用方法往往忽略了共轭负频率部分旁瓣泄漏的影响(如文献[5])。插值校正流程如图1所示。

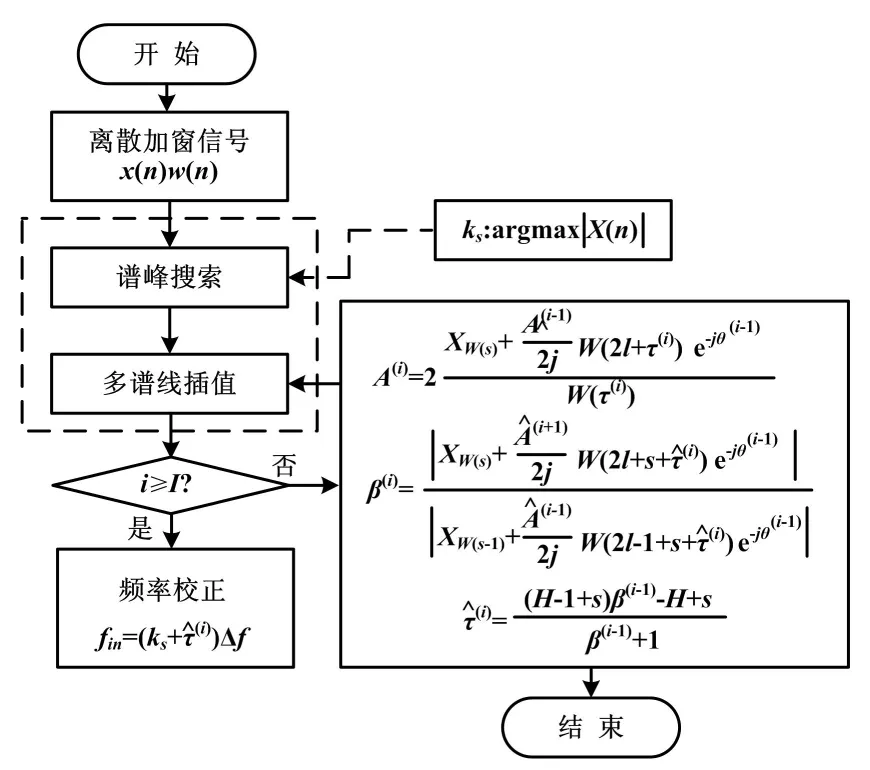
图1 插值校正流程图

为解决上述两个问题，文献[16-18]提出了采用迭代的提升插值离散傅里叶变换算法，对应流程如图1所示。该方法优点在于充分考虑了共轭负频率旁瓣衰减对校正方法的影响，即图1中迭代过程窗谱函数完整包含了负频率部分，对应公式为：

(9)

基于上述特点，迭代算法可以在很短信号周期内提供准确的谐波信号参数估计。但迭代过程的高额计算成本，使得其应用于实时计算时存在困难。

3 非迭代插值算法

①频率估计。

假设信号频率处于其对应离散傅里叶变换的第kp根谱线附近，联合峰值谱线左右两根次最大谱线(kp±1)，进而根据加窗傅里叶变换式(4)，可得：

(10)

式(10)可进一步化简为：

AB=0

(11)

式中：0为零矩阵。

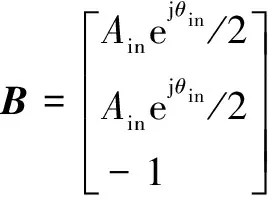
(12)

由于幅值和相位组成的变量矩阵不可能为0，因此方程系数矩阵的行列式ΔA等于0，即：

(13)

进一步根据式(8)，可得下述比例关系：

(14)

将式(14)代入式(13)，利用行列式性质，化简为：

(15)

通过对上述行列式分解，可得关于η的代数方程为：

Γ1-η2Γ2=0

(16)

(17)

则可得频率估计为：

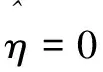
(18)

②幅值和相位估计。

假设：

(19)

则根据式(4)可得：

(20)

同理，联合左右两根次最大谱线(kp±1)，以矩阵方式重写式(20)，可得：

CD=E

(21)

矩阵C、D和E分别为：

(22)

D=[ab]T

(23)

E=[XR(kp)XR(kp)]T

(24)

联立式(21)～式(24)，采用最小二乘法，可得：

(25)

则幅值和相位分别为：

(26)

基于非迭代散点插值校正可精确得到单一频率信号参数估计。通过前述推导，上述估计方法可进一步扩展应用于谐波情况下各频次参数估计，具体差异在于式(11)和式(20)所对应的系数矩阵构造。

4 谐波电能计量

根据前述得到的被测信号基波和各次谐波分量的幅值、相位和频率，可完成基波和谐波电能精确计算。假设电网电压电流信号分别为：

(27)

根据IEC STD 61000-4-7，在k个基波周期T内，单一频率分量的标准谐波电能公式为：

(28)

则在计及基波及各次谐波正反向电能情况下，可得总电能为：

(29)

基于非迭代插值校正谐波电能计量流程如图2所示。

图2 基于非迭代插值校正谐波电能计量流程图

5 算法仿真分析

5.1 窗谱近似误差

窗频谱及对应近似误差如图3所示。

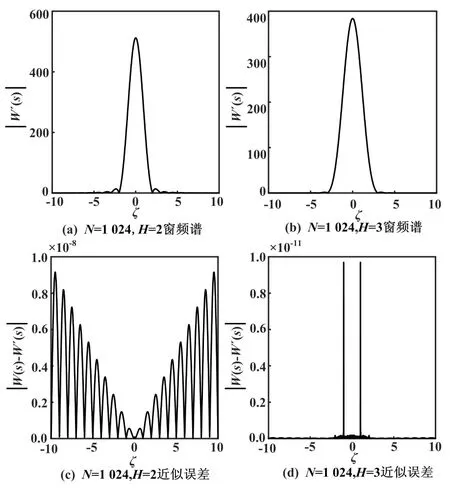
图3 窗频谱及对应近似误差图

在前述频率估计过程中，为满足方程解析过程需要，根据文献[19]近似得到最大衰减旁瓣余弦窗的频谱，因此需要分析近似可能带来的估计误差。其中，根据H阶最大衰减旁瓣余弦窗定义，其准确频谱根据离散时间傅里叶变换得到，为：

(30)

窗频谱近似首先会造成式(4)频域离散采样误差。而从图3可明显看出，在主瓣内W(ζ)与W″(ζ)近似误差非常小，基本在10-9范围以下，表明以式(17)和式(18)连续三频域离散采样点线性组合的频率估计是非常精确的。同时，用于方程求解的式(14)线性变换准确度也可以得到保证。

5.2 单一频率信号参数估计

假设单一频率离散采样信号为：

s(n)=Aincos(2πfinnT+θin)

(31)

此处参数设置分别为：幅值Ain=5;频率fin=49.52 Hz;初始相位θin=π/3;采样周期T=1/5 000 s。

上述信号充分考虑了实际电网信号频率波动范围，因而具有典型性。分别采用本文设计的非迭代三谱线插值和典型加汉宁窗三点权重插值方法。从结果可以明显看出，本文设计的方法较加汉宁窗三点权重插值方法精度高出约4个数量级，整体相对误差零级在10-6左右；值得特别注意的是在短时截断情况下，非迭代方法也可以准确得到信号参数，因而可应用于短时波动信号分析。

5.3 谐波电能计量

假设含谐波离散采样信号为：

(32)

谐波分量参数如表2所示。基波频率为49.8 Hz，采样频率为5 000 Hz。

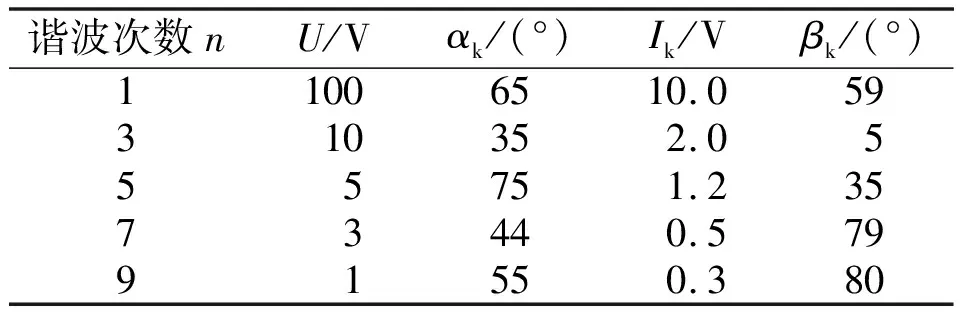
表2 谐波分量参数

首先，以电压作为分析对象，分别采用H=2、3、4、5所对应的4个不同离散时间窗，得到的不同阶窗函数下周期数与估计误差如图4所示。

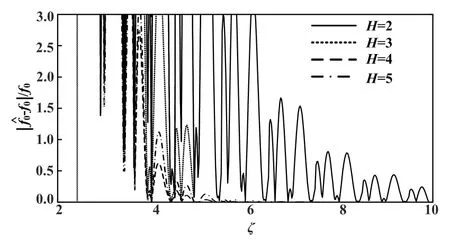
图4 不同阶窗函数下周期数与估计误差

最后以5个基波周期截断，分别计算电压、电流各次谐波幅值、相位，得到功率及误差，如表3所示。

表3 谐波分量误差

6 结束语

常用多点线性插值方法未考虑负频率共轭部分带来的长泄漏干扰，对于高精度谐波电能计量，会带来累积误差。本文提出的基于非迭代多点插值DFT精确谐波电能计量算法，充分考虑并消除了与共轭分量相关的参数估计结果的影响，利用多阶最大衰减旁瓣窗函数高精度近似，进一步消除近似误差对窗谱函数的影响。而采用稳健的三点线性组合方式，有效避免了幅值和相位波动对频率估计的影响，理论分析及仿真结果表明，该方法在短时窗情况也具有很高的计算精度，因而基于该非迭代插值方法的电能计量算法理论的可用于动态负荷谐波电能计量，较以往其他计量算法具有更广的适用性。

鉴于篇幅有限，本文未进一步就算法抗噪特性进行分析和仿真，因而下一步将重点研究算法在含噪声情况下性能评估和提升；同时，还将该算法进一步推广应用于非平稳信号参数估计，以解决复杂工况下谐波电能计量问题。