模糊自适应整定PID控制在纸浆浓度中的应用
2019-12-04曾德斌许江淳张矿伟杨杰超陆万荣李玉惠
曾德斌,许江淳,张矿伟,杨杰超,陆万荣,李玉惠
(1.昆明理工大学信息工程与自动化学院,云南 昆明 650500;2.玉溪师范学院物理与电子工程学院,云南 玉溪 653100)
0 引言
在造纸工业中,纸浆的浓度具有很多特性,例如时变性、非线性和滞后等。而在工业控制领域方面,又因为PID控制的原理相对其他控制而言具有简单和适应性强等优点,因此传统的PID控制在工业领域的地位则显得非常重要。目前,工业控制普遍采用的PID控制在参数整定方面消耗的时间较长、能量消耗较大;而且参数对整定对工业产品具有很大的影响,影响生产效率,甚至有可能不产出产品。如果利用人工去整定PID参数,人为因素成分影响又较大,同一参数在不同的专家整定结果都会存在一定的差异。即使参数都能够满足工业控制的需求,也有可能不是理想的工业控制参数。PID控制以造纸工业中的纸浆浓度误差e和纸浆浓度误差变化ec作为输入变量。模糊自适应整定PID控制在PID控制的基础上进一步利用模糊控制规则在线对其进行参数的自适应整定,从而满足造纸工业控制中的参数需求。
1 传统PID控制
在造纸工业中,纸浆浓度控制系统如图1所示。它主要由浓度传感器、控制器、调节阀等部分构成。
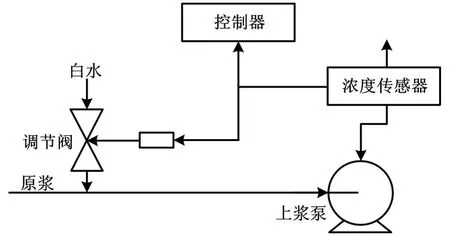
图1 纸浆浓度控制系统
传统的PID控制能够广泛应用在各行各业的控制过程中,主要是因为其结构相对简单、鲁棒性强等优点。传统PID控制系统原理如图2所示。传统的PID工业控制系统主要由PID控制器和被控对象这两部分构成[1]。在传统的PID控制中,只有对比例系数、积分系数和微分系数这三个参数依据实际的系统模型进行参数整定[2],形成既能相互配合又能够相互制约的关系,才能取得很好的控制效果,从而满足不同的工业控制需求。传统的PID控制系统往往能够根据不同的工业控制对象来对控制参数进行整定[3]。
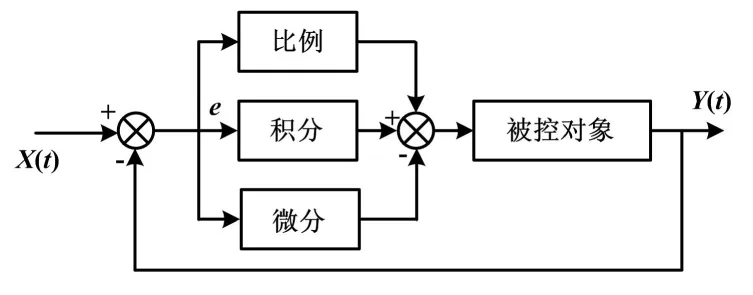
图2 传统PID控制系统原理图
PID的控制规律为:
(1)
式中:Kp、Ki、Kd分别为PID控制的调节器中的比例系数、积分系数以及微分系数。
通常对传统的增量式的PID控制算法进行离散化,具体的离散化的形式如式(2)所示:
Δu(k)=u(k)-u(k-1)=kp[e(k)-e(k-1)]+
kie(k)+kd[e(k)-2e(k-1)+e(k-2)]
(2)
式中:k为系统模型的采样信号;e(k)为系统在第k次采样时刻中的理论输出与实际输出之间的偏差值;e(k-1)为系统在第(k-1)次采样时刻的偏差值;u(k)为当前采样时刻的控制量。
实际上,在大多数的工业生产过程中,被控对象往往具有滞后、时变性等特点[4]。如果仍然要利用传统的PID控制器对其进行控制,在一定程度上就很难满足工业控制的要求,进而实现理想的控制效果。传统的PID控制在应用方面受到一定条件的限制。
2 Mamdani模糊系统
模糊系统主要由两种模糊推理系统模型组成:一类是Mamdani系统模型,它的模糊推理规则的后件是输出量的某一模糊集合,通常又被称为模糊系统的标准模型[5];另一类是模糊规则的后件是输入语言变量的函数,其典型的情况是输入变量的线性组合[6]。
在Madani型的模糊逻辑推理系统中,它的模糊语言值是模糊规则的前件和后件。其具体的形式如下所示。
IFxiisA1andx2isA2and……
andxnisANTHENyisB
其中:Ai(i=1,2,…,n)是输入语言值;B是输出模糊语言值。
基于Mamdani模型的模糊逻辑系统原理如图3所示。Mamdani主要由许许多多的“IF THEN”来构成它的模糊规则库。
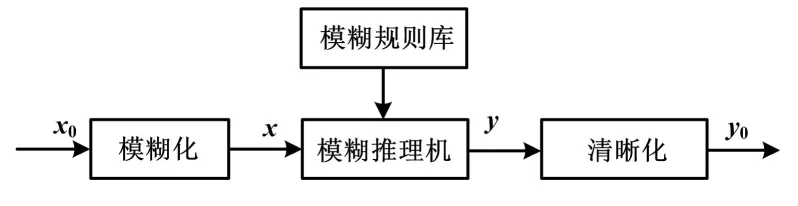
图3 基于Mamdani模型的模糊逻辑系统原理图
Mamdani采用一阶梯度寻优算法调节,如式(3)、式(4)所示:
(3)
(4)
在求得文中的系统模型的一阶梯度后,参数调整的Madani学习算法通常是最后步骤,如式(5)~式(7)所示:
(5)
(6)
(7)
3 模糊自适应整定PID控制
3.1 模糊自适应PID控制原理
模糊自适应PID控制系统能够对控制过程中的许多因素进行检测分析,例如其他一些不确定的条件、迟滞等因素,再利用模糊推理的控制规则方式在线自适应整定PID的Kp、Ki、Kd参数,从而实现在线自适应整定参数。模糊自适应PID控制系统结构如图4所示。
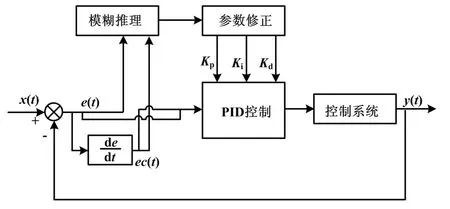
图4 模糊自适应PID控制系统结构图
由图4分析得知,基于模糊自适应PID控制系统主要由两大功能模块组成[7]:PID控制器控制模块、模糊控制器的参数整定模块。在模糊控制器的参数整定模块中,系统把纸浆浓度偏差e(t)和纸浆浓度偏差变化量ec(t)作为模糊系统的输入变量,PID控制器的ΔKp、ΔKi、ΔKd作为模糊控制器的输出变量和PID控制器的输入变量;然后再根据预先规定的模糊规则,对其参数的整定进行模糊推理,从而实现在线实时调节PID控制器的参数。
3.2 模糊自适应PID控制器设计
因为造纸工业中对于精度以及多维度有需求的模糊控制系统模型有益于提升系统的控制精度,然而又因为高维度的控制系统的控制规则太繁杂,会导致控制算法难以实现等一系列的问题。通过对造纸行业的纸浆浓度进行综合分析以及文献查阅,用二维的模糊控制器作为模糊自适应PID控制系统的控制器。
①确定系统的输入输出变量。由系统模型分析可知,该模型的核心为纸浆浓度中的水分控制,而水分主要由PID控制器控制,PID控制的参数的整定部分是由模糊控制器进行在线自适应整定。本文选取以e及ec作为模糊控制器的输入变量,PID控制参数的变化量ΔKp、ΔKi、ΔKd作为模糊控制器的输出。
②定义模糊子集。对整个纸浆浓度的系统模型进行综合分析,定义了e和ec为模糊控制器的输入变量,而模糊控制器的输出变量为ΔKp、ΔKi、ΔKd。对输入输出的模糊子集为进行了预定义,分别为{NB(负大),NM(负中),NS(负小),Z0 (零),PS(正小),PM(正中),PB(正大)},定义它们的模糊论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。
③确定隶属函数。模糊子集的语言变量论域文献中,通常采用隶属度函数来进行函数描述。这是因为隶属度函数往往能够对事物的模糊性进行一个很好的描述。隶属度函数由线性的隶属度函数和非线性的隶属度函数两大类构成[8]。其中,以三角形隶属度函数、高斯型隶属度函数、梯形隶属度函数、S型隶属度函数等隶属度函数最为常见。本文综合分析了纸浆浓度的特性,用三角形隶属毒函数作为本文的隶属度函数。三角形隶属度函数的具体形式如式(3)所示:
(3)
④建立模糊控制规则表。模糊控制器的e及ec的隶属度函数如图5所示。模糊PID控制器的ΔKp、ΔKi、ΔKd的控制规则如表1所示。
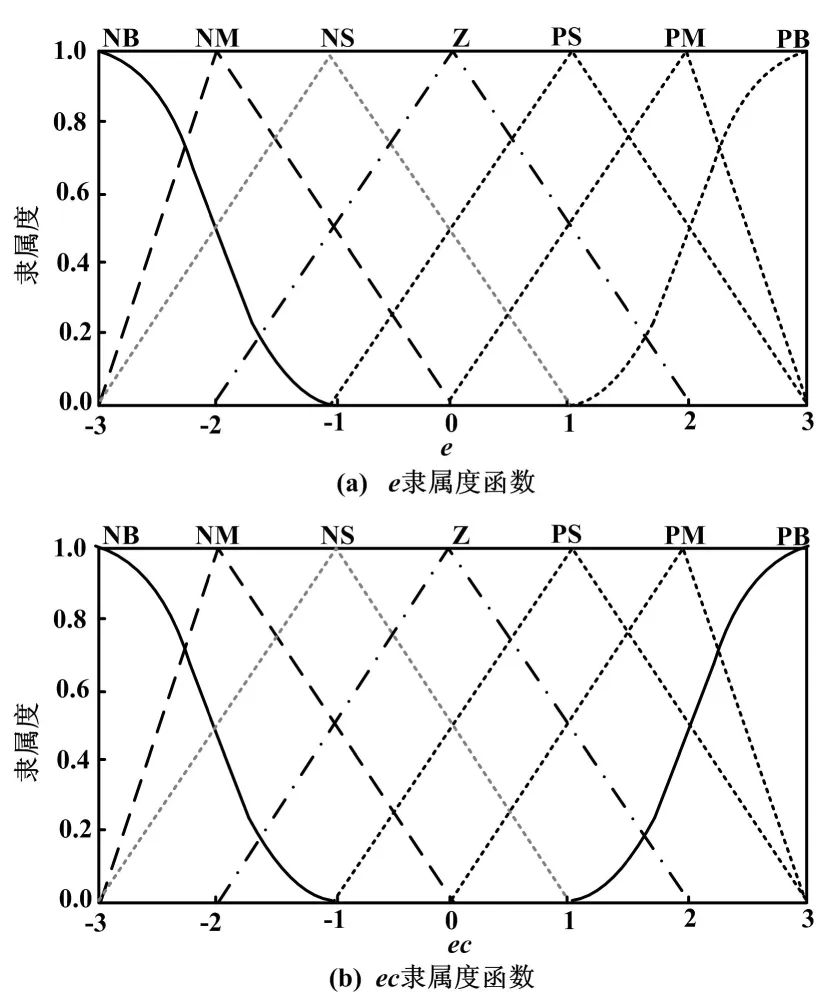
图5 隶属度函数
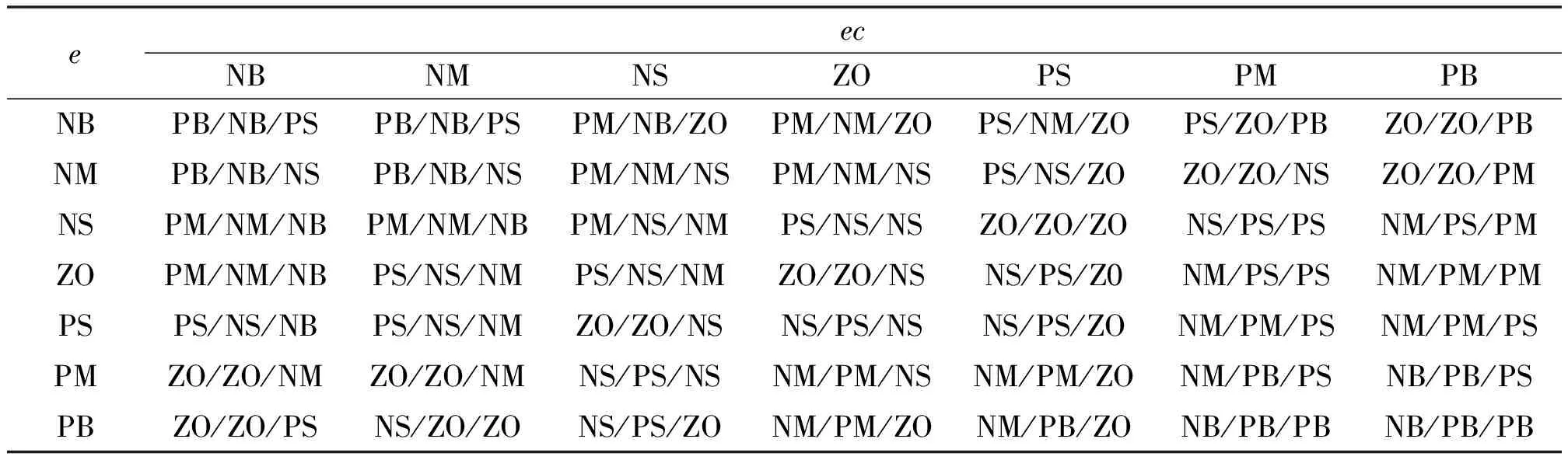
表1 模糊PID控制器的ΔKP、ΔKI、ΔKD的控制规则
根据预先定义的模糊控制规则,可以将模糊控制规则表改写为以下的“IF THEN”形式。
运用模糊自适应的规则去整定PID控制器的关键参数,参数表达式如式(9)所示。
(9)
式中:Kp0、Ki0、Kd0均为系统预先赋值的初始值;ΔKp、ΔKi、ΔKd均为模糊自适应控制器的输出值。
⑤模糊推理及解模糊。文中采用Mamdani推理方法对纸浆浓度进行模糊推理,而在工业控制领域则主要采用加权平均法进行解模糊。输出值由式(10)决定。
(10)
4 纸浆浓度仿真试验
在造纸工业中,不同的纸张质量对于纸浆浓度的要求也不一样。因此,纸浆浓度控制系统中的过程参数主要由纸张的质量要求所决定。当生产80 g/m2的纸时,它的纸浆浓度的控制系统的传递函数如式(11)所示。
(11)
在Matlab中构建一个以e及ec作为系统模型的输入,以kp、ki、kd作为系统模型的输出。
当生产80 g/m2的纸时,本文采用传统PID控制和模糊自适应PID控制两种控制系统对纸浆浓度的系统模型进行仿真。
无扰动的系统响应如图6所示。

图6 无扰动的系统响应图
从图6分析得知,模糊自适应PID控制在进入稳态时间短于传统的PID控制,而且振荡的幅度也比传统的PID控制[9]。
有扰动的系统响应如图7所示。
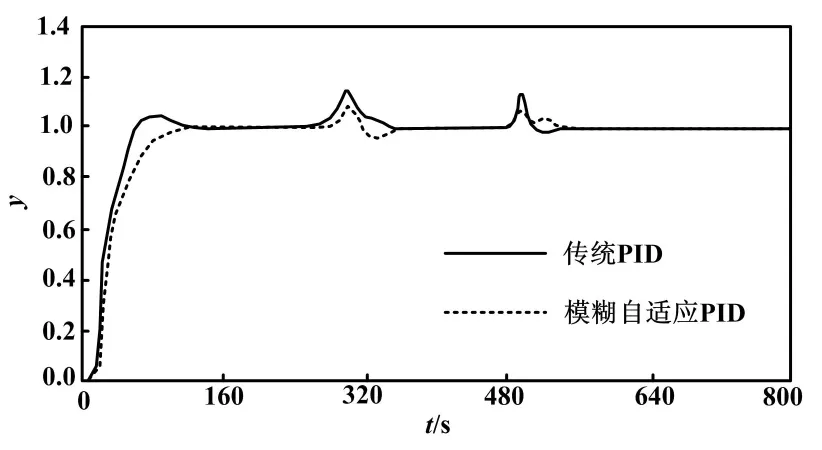
图7 有扰动的系统响应图
由图7可知:传统的PID控制在有干扰的情况下往往会产生较大幅度的振荡;而模糊自适应PID控制即使是在有同样的干扰情况下,振荡的幅度也比传统的PID控制的振荡幅度小,而且恢复到稳态的时间也快于传统的PID控制。
由以上试验结果可知,模糊自适应PID控制不仅在抗干扰能力、稳态性能、振荡幅度等方面明显优于传统的PID控制,而且它的调控性能明显优于传统的PID控制。
5 结束语
在造纸行业中的生产过程中,纸浆浓度的稳态调节对达到不同纸张质量标准要求起着举足轻重的作用。参数整定问题长期以来都是传统PID控制器的缺陷[6-10]。本文将模糊推理技术与传统的PID控制技术相结合,使用模糊自适应PID控制,能够实现对Kp、Ki、Kd的实时在线自适应参数整定,适用性较强。
