一种基于深度神经网络的调制盲识别方法*

吕 荧

（驻广州第二军事代表室，广东 广州 510000）

0 引 言

在现代无线通信中，信号调制盲识别具有重要的作用。随着电磁环境的日益复杂，正确识别出通信信号的调制类型是实现后续解调和译码的前提。因此，对于认知无线电[1]与非合作通信系统，调制盲识别作为一项关键技术有着很高的研究价值。信号调制识别技术在军事和民用通信领域的应用十分广泛，如无线电监测、干扰源辨别分析、智能信号传输和网络电磁对抗等方面。美军联合战术无线电系统JTRS中运用调制识别算法对信号样式进行识别，从而提供给各类电台之间相互通信的重要波形类别参数。在2016年自适应认知电子战行为学习（Behavior of Learning and Adaptive Detection in Electronic-war，BLADE）项目中，其装备将实时分析调制类型等，能够快速识别并描述威胁信号。在民用监测接收机方面，德国R&S公司的ESMD、美国Keysight公司的E3238S分析仪等，都通过调制盲识别技术获取采集数据的调制类型，有助于开展频谱管理任务。调制盲识别方法也可用于电子对抗中对雷达脉内识别的实现，为判别雷达个体目标属性（Specific Emitter Identification，SEI）等工作打下了基础。开展调制盲识别技术研究，已受到了许多国内外研究学者与机构的高度重视和关注。

传统的调制盲识别技术包括基于统计特征的方法和基于最大似然准则的方法[2]。一般来说，基于统计特征的方法的思路是依靠接收数据的统计模型，使用概率论等得出信号的特征参数。一些新思路则可以通过基于机器学习等良好的人工智能分类决策方法实现识别。这类算法能够在缺乏先验知识的情况下，利用数据学习模型进行训练，可以获得较好的分类性能。信号的调制盲识别在本质上可分成两个步骤：特征提取与分类。其中，过去常用的分类器有决策树、支持向量机（Support Vector Machine，SVM）等，但是在实际环境中识别性能并不理想。以前的一些算法多集中在高斯白噪声信道情况下的分析，而在衰落信道中识别率将明显降低。因此，本文提出了一种基于深度神经网络的改进识别思路。该算法首先通过对实际复杂信道中的信号多种统计特征进行分析，合理选取出与调制信号具有强相关性的特征，然后将挖掘的统计特征数据输入深度神经网络（Deep Neural Network，DNN）分类器，利用其高维尺度适于对复杂数据结构分类的优势，可以得到在衰落信道中的更好识别效果。新方法在低信噪比条件下正确识别率较优，可识别BPSK、QPSK、8PSK、16QAM和64QAM等多种调制信号，在处理过程中还进行了优化，减少了运算开销，具有工程实用性。

1 信号模型分析

数字基带信号r(t)的计算模型通常可表示为：

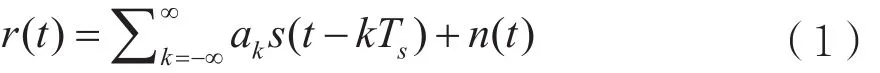
其中Ts表示数字信号的符号周期，ak表示调制的信息符号，n(t)表示噪声信号。s(t)为信号总的脉冲响应，包括脉冲成型滤波器、匹配滤波器和信道冲激响应等。在衰落信道中，s(t)的幅度是时变的，且变化量由多普勒频偏fc确定。接收端信号的离散样本点可由对信号r(t)在t=nT时刻进行采样得到，其中T表示采样周期，Ts/T表示过采样因子。

图1为流程框图。首先把系统接收端的通信信号进行滤波、正交变频等预处理操作，然后通过从信号样本中提取有用的参数特征，包含时频域特征和其他各种变换域特征。对于复杂的电磁环境，预处理模块能够在一定程度上实现去噪、去干扰等，保证特征参数提取模块输入合适的信号数据。在调制分类部分，需精确区别判断信号样式，因此设计合适的分类思路十分关键，会影响调制样式识别正确率。通常有统计模式结构分类思路、神经网络型结构分类思路以及决策型结构分类思路等，其中决策型结构分类思路实现比较简单，更符合工程实际应用。

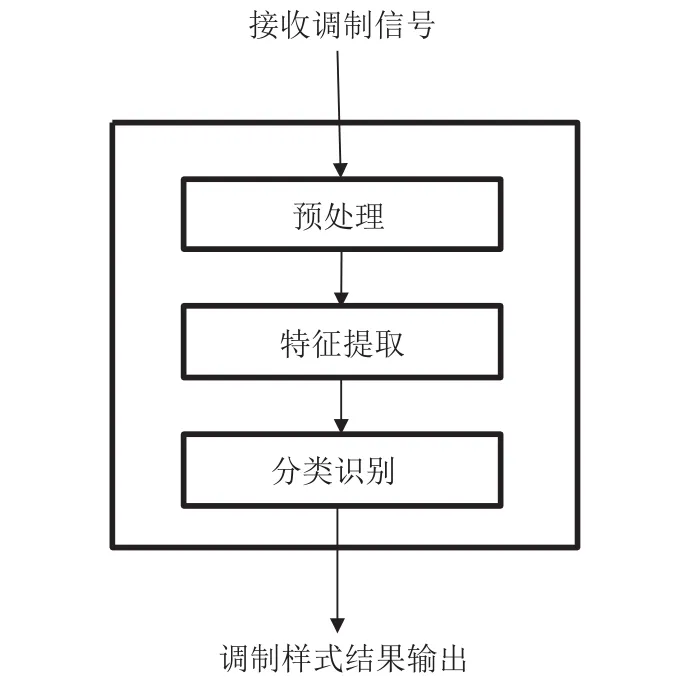
图1 信号调制样式识别总体流程

2 算法分析与改进

2.1 特征提取方法分析

特征提取作为调制识别中的重要部分，可为后续待开展的识别分类工作提供正确的参数特征基础[3-4]。

为了提供丰富的调制类型信息，本文分析选取了多种统计特征，包括高阶累积量特征、互熵特征和偏斜度特征等。

2.1.1 高阶累积量特征

设Cnm表示m个共轭变量的n阶累积量，则n个变量x1,…,xn的联合累积量可表示为：

其中，π在集合{1,…,n}的所有分区列表中运行，B遍历π的分区中所有块的列表，E(·)代表数学期望运算符。

对2阶累积量进行计算的表达式为：

对4阶累积量进行计算的表达式为：

对6阶累积量进行计算的表达式为：

2.1.2 偏斜度特征

这两种特征都可由标准差计算推导得出。偏斜度变换量σv可表示为：

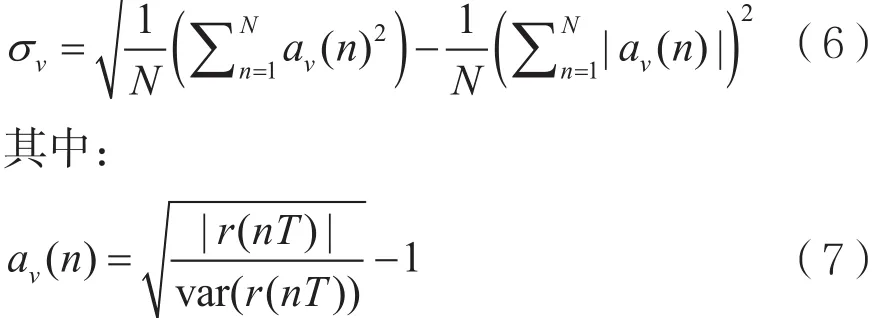
其中，var(.)代表数学方差运算符，r(nT)表示信号在t=nT时刻的离散样本。

2.1.3 互熵特征

调制类型的互相关性可用特征和类标签之间的互熵信息进行计算，第i个特征xi与类标签c之间的互熵特征计算式可表示为：

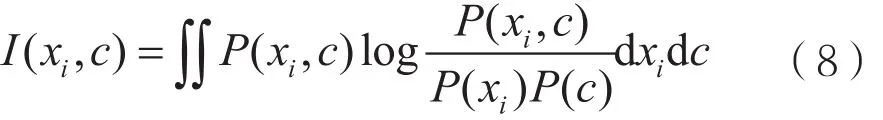
上述3种特征，在缺少联合分布P(xi,c)先验信息的情况下，可通过Pazen加窗方法实现对互熵的定量估计。调制类型的相关性越强，互熵的值越大。设衰落信道中的多普勒频偏为100 Hz，表1给出了高斯信道和衰落信道环境中28个特征互熵信息计算值的递减顺序。

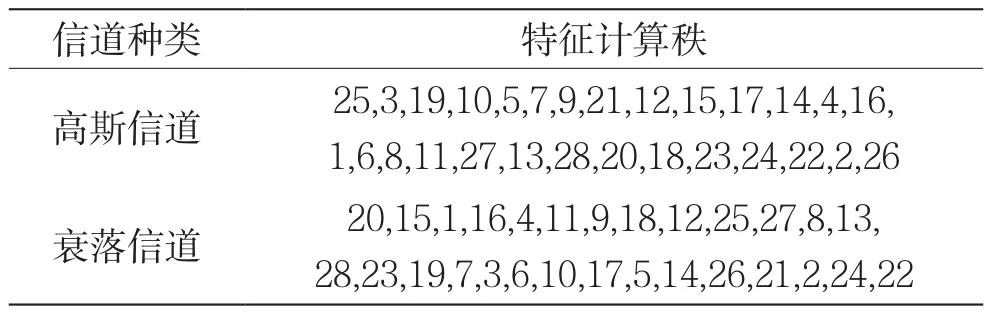
表1 两种信道中的互熵秩

2.2 神经网络分类器分析

深度神经网络（Deep Neural Networks，DNN）是一种典型的机器学习算法，常用于对数据进行分类，利用其高维尺度适于对复杂数据结构分类的优势，得到优良的识别效果。基于深度神经网络的信号样本训练器，通常采用基于反向传播类型的神经网络进行数据信号样本的训练，且用负对数似然函数作为代价函数，因此可在衰落信道中得到优化训练的样本数据。一般可选择20%的数据用于评估检验。当检验误差在迭代过程中减少时，学习速率也将降低。实际处理时，使用16 000个信号特征向量训练神经网络，其中20%用于验证，从而可用10 000个测试样本评价分类精度，初始学习率设为0.01，训练单元包含的样本数量设为50。

图2为一种对BPSK、QPSK、8PSK、16QAM和64QAM调制信号的深度神经网络分类器结构图。

图2 使用神经网络的分类结构

图2 的神经网络分类器具有4层隐层的全连接前馈结构，可使用校正线性单位函数作为非线性函数。输入到输出各层的隐含节点数分别设为500、200、40和5。在输出层，可选用归一化指数函数（softmax）生成与前述待识别的5种调制样式的相关概率统计数。处理时应将输入到神经网络中的各个信号特征向量元素进行归一化，能够得到以最大概率输出的调制识别结果。不同于其他类型的分类识别思路，DNN分类器在特征空间维数较高的情况下也能很好地从大量特征中提取有用信息，并提供良好的识别性能。

3 仿真结果及性能分析

仿真参数如下：采样率200 MHz，频率70 MHz，码速率1 Mb/s，样本点数8 192，仿真次数2 000次，噪声为高斯白噪声。采用本文方法进行信号调制样式识别，得出正确识别率，仿真结果如图3所示。

从图3可以看出，本文方法是一种有效的信号调制样式识别方法。在SNR＞5 dB时，对各调制种类的识别正确概率可达到90%以上。

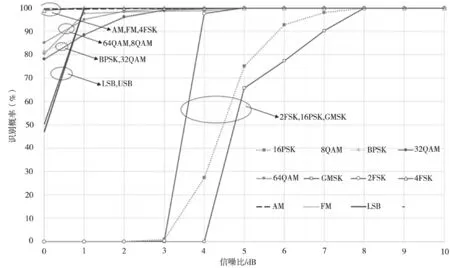
图3 此处方法对各调制样式的正确识别率曲线

对过去的传统基于最大似然判决方法和本文的方法进行性能仿真比较，横轴表示信噪比，纵轴表示调制样式的平均识别率，结果如图4所示。

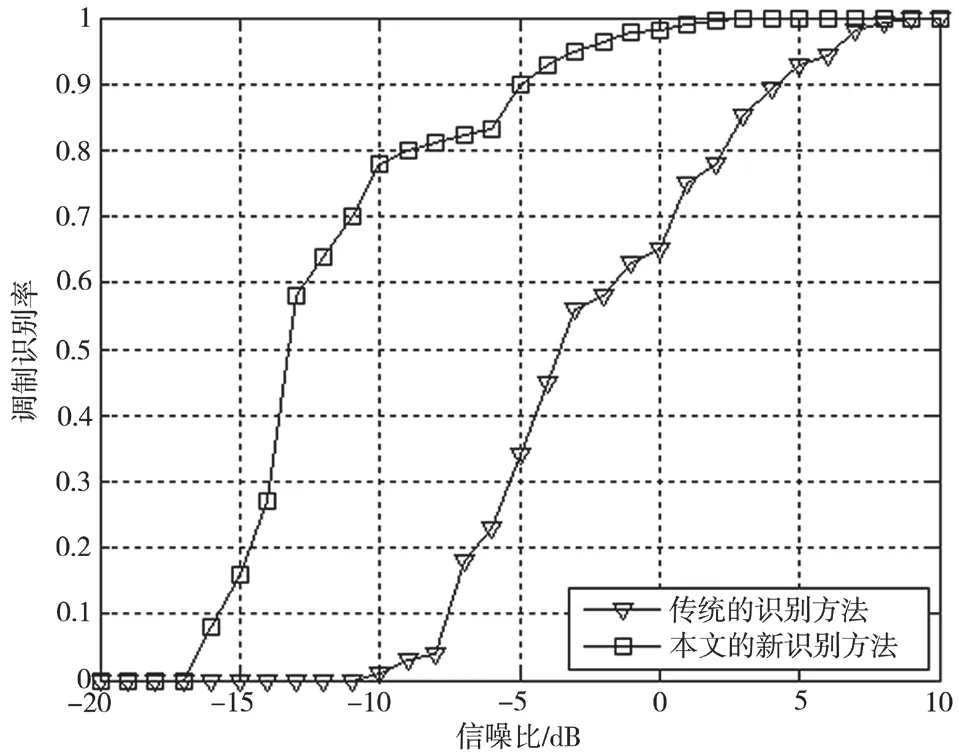
图4 本文中方法与过去传统方法的性能比较

可以得出，新方法比起过去一些调制样式识别方法，性能表现更优。

4 结 语

随着通信技术的不断发展，信号的调制类型变得复杂多样，并需要考虑实际信道环境，从而对调制类型盲识别研究提出了更高要求。本文提出了一种基于多种特征提取结合深度神经网络（DNN）分类器的融合改进方法。仿真表明，该方法相对于传统的识别算法能够改善调制盲识别的分析性能。今后将进一步优化，为解决信号调制盲识别问题提供一种更有效的手段，并且为网电对抗领域的研究贡献力量。