一种Kannala模型的鱼眼相机标定方法优化

张春森，严 露，于 振

（西安科技大学 测绘科学与技术学院，陕西 西安710054）

0 引 言

三维重建技术已被广泛的应用于生活和科研工作中，特别是在街景重现、城市导航、文物保护、工业设计等方面［1］，展现出了极强的生命力和影响力。三维重建技术的重点在于如何获取目标场景或物体的深度信息［2］。在景物深度信息已知的条件下，只需要经过数据的配准及融合，即可实现景物的三维重建。在这一过程中，鱼眼相机由于视角范围大，可以达到甚至超过180°［3］，为近距离拍摄大范围场景创造了条件，同时也为三维重建提供了便利。但是鱼眼相机拍摄的图像存在较大的畸变，不能直接用来匹配应用，需要对图像进行校正。在现有的校正方法中，通常需要首先对鱼眼相机进行标定获取包括等效焦距、图像中心、畸变系数等相关参数［4］。

Geyer等提出适用于摄像机系统的中心折反射式球面统一模型用来进行鱼眼相机的标定［5］。Ying等将鱼眼相机拍摄的标定图像的空间线投影到一个大圆圈，利用投影在大圆圈的数学关系优化相机参数，由于没有对空间线之间的位置进行约束，只能作粗略估计［6］。Scaramuzza等假设利用泰勒级数的展开描述相机的成像过程，其系数为需要校正的相机内参数。用于估计参数的四步线性最小二乘法，与普通最小二乘法相比，此方法更准确［7］。刘凤英等针对于全景相机利用光束法空三平差法获得了精确的标定参数［8］。程梦娇等通过激光扫描仪获取需要标定空间的三维点云图，然后利用SIFT算法描述相机与扫描数据的对应关系，并进行选择，剔除不需要或误差大的特征点，采用三维随机采样一致性滤波器对相机标定的参数进行估计［9］。林春雨等根据相机成像坐标系之间的转换，可获得该点的物理尺寸及相机焦距，得出相机标定的内参矩阵和旋转矩阵［10］。

Kannala在等距投影模型的基础上提出了一种通用的多项式形式的鱼眼相机模型［11］。然而基于多项式的畸变函数表示方法有局限性，由于高次多项式在计算上的复杂性，当畸变函数的设计较为复杂时，多项式模型的求解计算误差会很大［12］。为此，文中给出了一种采用分段多项式逼近的鱼眼相机检校模型［13］，以实现对多项式函数模型的优化，通过对鱼眼相机获取的真实场景影像的三维重建，证明了所给方法能有效提高模型标定的计算效果。

1 鱼眼相机的相机模型和畸变

1.1 常用的鱼眼相机模型

普通相机成像遵循的是针孔相机模型，在成像过程中实际场景中的直线仍被投影为图像平面上的直线［14］。如果使用针孔相机成像模型，当鱼眼相机的视场角到180°时，投影到成像平面的场景将会变的无限大。所以，为了让鱼眼相机拥有较大的视场角并且可以将图像投影到有限的成像平面，须允许相机畸变的存在。在这些畸变中，最严重的畸变是径向畸变，因此主要考虑径向畸变对相机成像的影响。目前，用于模拟鱼眼相机成像过程的模型包括4个模型：等距投影模型，等立体角投影模型，正交投影模型及体投影模型。Kannala鱼眼相机一般多项式近似模型是基于等距投影模型提出的。

式（1）为等距投影关系式，θ为成像点p与投影中心连线与主轴的夹角；f为焦距；r为投影中心到成像点之间的球面半径。

由高斯光学求得径向放大率为式（2）

切向放大率为式（3）

根据式（1）和式（3）可得式（4）

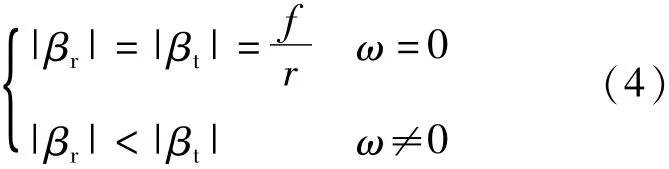
由式（4）可得到如下结论

1）视场角相等的点在像面上有等径向距离［15］，称之为“等距投影”；

2）等距投影的鱼眼相机，对于给定的球面物成像时，其径向放大率βr不变。切向放大率随θ的增大而变大。

1.2 鱼眼相机的畸变

为了使鱼眼镜头的视角非常大，设计者必须做出牺牲，以允许鱼眼图像产生更大的变形。这种变形包括径向畸变、切向畸变和薄透镜畸变［16］。

1.2.1 径向畸变

径向畸变是沿着透镜的径向在畸变中心处的图像像素中心的畸变，即远离透镜中心的地方产生的形变更大。径向畸变主要包括远离光轴和靠近光轴产生的枕形畸变和桶形畸变。枕形畸变的形成是由于图像的中心向光轴中心靠拢，如图1（a）所示。桶形畸变的形成是由于图像的中心偏离光轴中心，如图1（b）所示。径向畸变的表示可以根据泰勒级数展开的前几项进行表示，经过校正的坐标为式（5）

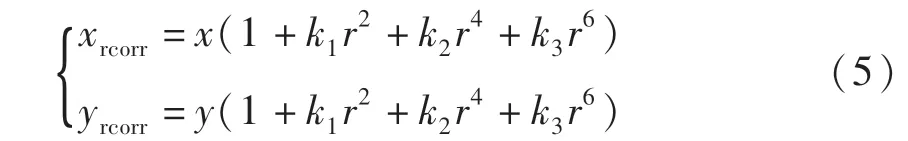
图1 径向畸变示意图Fig.1 Radial distortion diagram

1.2.2 切向畸变

切向畸变是由于安装误差而引起的畸变，因为切向畸变的存在，一个矩形投影到成像平面上可能会变成梯形。切向畸变由参数p1和p2描述，经过校正的坐标为式（6）

1.2.3 薄棱镜畸变

薄棱镜畸变是由于镜头的设计、制造和装配的过程中存在误差造成了图像的畸变，称为薄棱镜畸变［17］。与径向畸变和切向畸变做比较可知，鱼眼相机的畸变类型中影响相对较小的畸变是薄棱镜畸变。如果引入全部的畸变会增加畸变参数，从而造成计算复杂并且难以求解，为此主要考虑对成像影响比较大的径向畸变和切向畸变，综合上述可以用参数k1，k2，k3，p1，p2来描述。

2 基于多项式的鱼眼相机标定

2.1 Kannala相机模型

Kannala提出了一个鱼眼相机的一般近似模型，该模型是基于等距投影模型［18］提出的。Opencv中使用的正是Kannala提出的鱼眼相机的一般近似模型。公式（7）给出了统一写成等距投影模型的鱼眼相机模型。

式中 θd为θ的奇函数，将θd进行泰勒展开可以得到θ的奇次多项式，Kannala取前5项就可以很好的近似各种投影模型，并且针对于各种投影模型有充足的自由度。式（8）为θd的泰勒展开的前5项。

根据多项式模型得到空间点到鱼眼图像点的变换过程如下，世界坐标［XW，YW，ZW］到相机坐标［XC，YC，ZC］的转换关系为式（9）

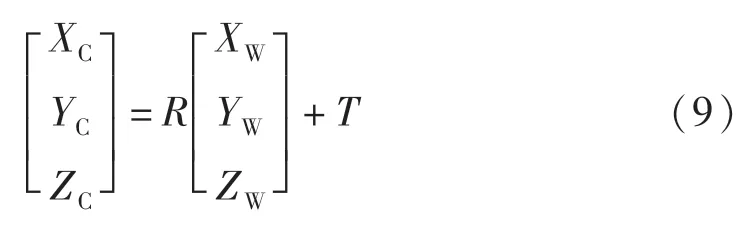
式中

2.2 分段多项式逼近模型

用多项式逼近函数［19］时，一般认为多项式系数越高逼近效果就越好，但是当次数越来越高时，进行插值会出现龙格效应。为了使拟合效果更好，同时避免龙格效应，选择分段多项式插值法。已知函数f（x）的分段线性插值函数IN（x）一般形式如式（14）

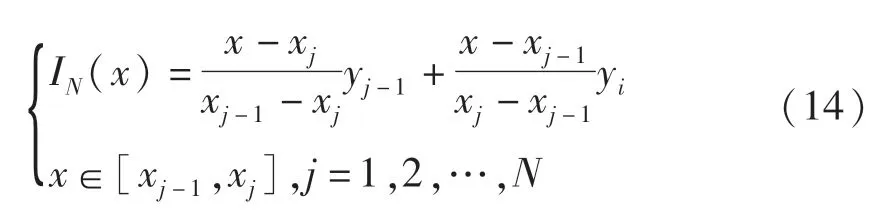
式中yi为函数f（x）在xi处对应的值。可以证明当节点加密时，分段线性插值函数与被插函数有很好的近似性。尽管分段插值函数可以很好地拟合被插函数，但是在节点处，插值函数一般不可导。为此，引入3次样条插值。即使用3次样条函数作为插值函数。3次样条函数定义为：给定区间［a，b］的一个划分Δ，如果函数s（x）满足以下2个条件则s（x）称为3次样条函数。

1）s（x）在一个小区间［xj-1，xj］（j=1，2，…，N）是一个3次多项式；

2）s（x）在整个区间上有连续二阶连续导数。最小二乘法是通过最小化拟合函数与被拟合函数之间的误差平方和寻找最佳拟合函数，即最小。

可以用2-范数的形式表示

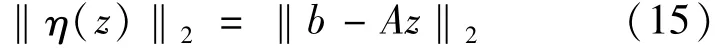
‖·‖定义为2-范数，η（z）=‖b-Az‖2定义为误差矢量［20］。可以证明，方程组的最小二乘解是唯一的，可以用式（16）的形式表示

3 实验与分析

3.1 相机标定及结果

采用12×9的黑白棋盘格为鱼眼相机标定板，通过对标定图像采集、棋盘格角点提取、以及基于C/C++语言结合Open CV 3.0编写标定程序，最终得到鱼眼相机参数。

实验使用GoPro生产的HERO4 Black鱼眼相机进行12次有效拍摄，并用文中所给的算法进行相机标定与影像校正。图2为鱼眼相机检校模板原始影像，图3为检校模板角点检测结果，表1为鱼眼相机标定结果，包括内参数和镜头畸变系数。为测试检校参数的准确度，对原始检校模板影像进行校正恢复，结果如图4所示。

图2 原始鱼眼图像Fig.2 Original fisheye images

表1 图像标定结果Table 1 Image calibration results

3.2 实验分析

如图4所示，针对某些校正图像中出现“拉伸”的情况，主要原因是在进行拍摄时，标定板相对于相机是倾斜的，并不与相机光轴垂直，所以会出现近大远小的情况，也就是“拉伸”的情况。相对于人的视觉情况而言，虽然感觉图像存在“拉伸”，但根据透视原理，符合空间分布情况。

对于拍摄的照片，分别利用文中方法和传统Kannala模型对鱼眼相机进行标定，得到了不同模型计算出的相机的平移矩阵和旋转矩阵，以此计算每张图像的反投影误差（表2），图5为可视化的反投影误差，可以看出：利用文中所给方法图像的误差有了明显降低，总体平均误差为0.012 417 1 pixel，与传统Kannala模型的0.029 267 6 pixel相比，降低了0.016 850 5 pixel.

图3 角点检测结果Fig.3 Corner detection results

图4 鱼眼图像校正效果Fig.4 Correction effect of fisheye image

表2 反投影误差分析Table 2 Analysis of back projection error

为进一步验证文中标定方法及所得相机参数的有效性，基于多视图立体视觉对影像目标进行三维重建并与无相机检校参数三维重建进行比较，图6为利用检校获得内参数和畸变系数对原图像进行校正比较，图7，图8分别为采用多视图立体技术将SFM产生的稀疏点云稠密化过程中的影像特征提取与匹配以及点云重建。图9分别为无相机参数及有相机参数三维重建比较。如图9所示，当加入相机参数和畸变系数之后，明显改善了图像扭曲的问题，显示的纹理特征比较全面，得到的三维模型更加真实。

图5 反投影误差Fig.5 Back-project errors

图6 原始图像与校正图像Fig.6 Original image and corrected images

图7 特征提取与匹配Fig.7 Feature extraction and matching

图8 点云重建Fig.8 Point cloud reconstruction

图9 三维模型Fig.9 Three-dimensional model

4 结 论

1）在研究Kannala提出的基于多项式的鱼眼相机成像模型（Kannala模型）的基础上，建立分段多项式逼近模型对其进行了优化改进。

2）通过设计标定板，使用GoPro生产的HERO4 Black鱼眼相机进行拍摄，利用C/C++语言结合Open CV 3.0编写标定程序，得到相机的内参数和畸变系数，并用其校正原始图像。

3）利用反投影误差定量分析传统Kannala模型和文中算法的相机标定的计算效果。对原始图像和校正图像结合运动恢复结构（SFM）进行特征提取和立体匹配，获得加密的三维点云。根据Meshlab对加密的三维点云进行网格化处理，分别获得原始图像和校正图像的多视图立体视觉三维重建模型，定性分析文中算法的优越性。