离散余弦拟谱方法求解反应扩散方程
2019-12-03张荣培杨程程
张荣培, 杨程程, 刘 佳
(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 沈阳师范大学 大学外语教学部, 沈阳 110034)
0 引 言
离散余弦变换(discrete cosine transform,DCT)主要用到余弦函数逼近给定样本函数的最小二乘和插值[1],在信号处理[2]、图像压缩[3]以及偏微分方程求解领域[4-5]得到了广泛的应用。由于DCT能够将空域的信号转换到频域上,具有良好的相关性的性能。
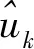
其次,将离散余弦变换应用于求解偏微分方程。将要逼近的函数u的最小二乘余弦插值多项式代入微分方程,余弦拟谱离散化应用于空间导数,然后在这些离散点集上应用配置方法,结合离散余弦变换,最终得到关于频域上的常微分方程组。通过向后Euler方法离散时间导数使之具有更好的稳定性,应用Picard迭代求解非线性代数方程组。在求解过程中,使用了快速余弦变换,提高了计算效率。
1 离散余弦变换
首先,将求解区域划分成J个网格,然后取每个网格的中心点得到离散点集。对于函数u,将[a,b]剖分为J个网格,定义
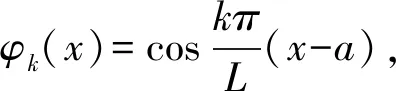
定理1 当-(2J-1)≤k≤2J-1时,有
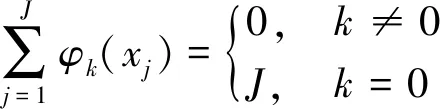
(1)
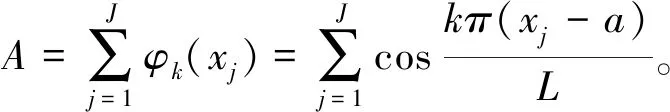
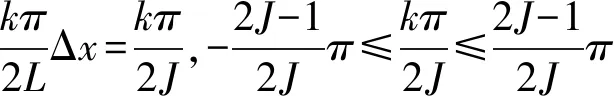
故得证。
定理2 函数{φk},k=0,1,…J-1在点集{xj}上正交,即
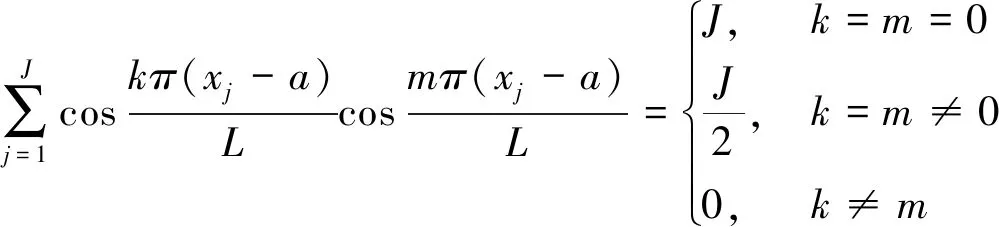
(2)
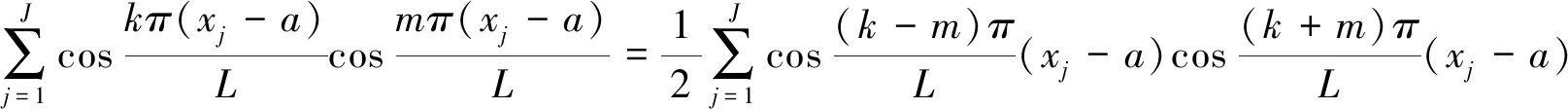
当k=m时,式(2)显然成立。当k≠m时,即k-m≠0,有-(J-1)≤k-m≤J-1,1≤k+m≤2J-1由定理1可证。
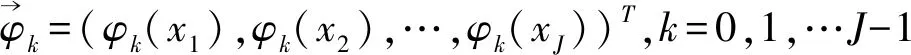
这说明了余弦函数{φk},k=0,1,…,J-1在点集{xj}(j=1,2,…,J)上是正交的。
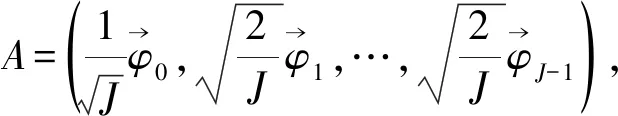
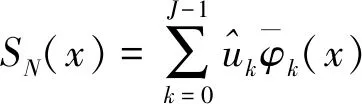
(3)
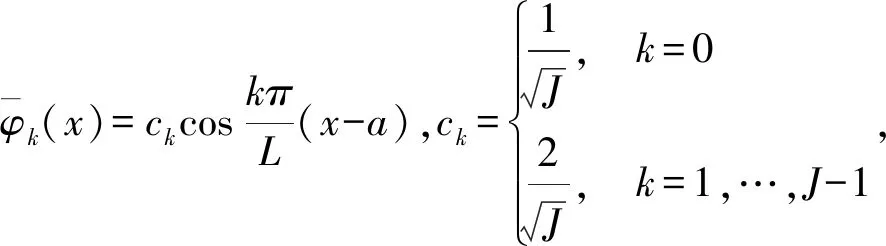
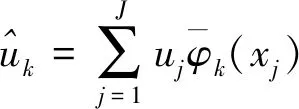
(4)
如果将离散点集代入最小二乘余弦逼近多项式(3)中,得到函数值uj等于SN(xj)。下面给出证明,

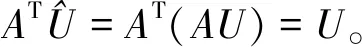
(5)
2 在反应扩散方程中的应用
反应扩散方程(组)是一类非线性偏微分方程,在生态学[6-8]、燃烧学[9]和化学反应流[10]等领域有着重要的应用。近年来,许多学者对该方程提出了许多数值方法,比如紧致积分因子法[11]、间断有限元法[12]、 格子Boltzmann方法[13]。下面将上面的离散余弦变换应用于求解偏微分方程,得到余弦拟谱方法[14]。考虑如下一维反应扩散方程
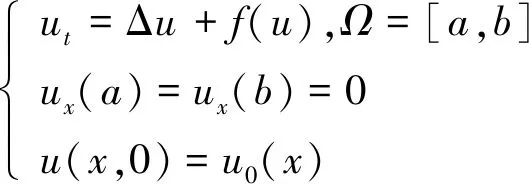
(6)
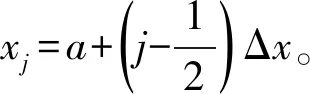
由定理3和上述二阶导数离散得

该非线性方程组可由如下Picard迭代法求解
3 数值算例
下面给出反应扩散方程的一些算例。在凝胶反应中,Gray-Scott方程模拟化学反应。对应的无量纲反应扩散方程为
其中:u,v为系统变量,代表反应物——基质和催化剂的浓度;Du,Dv为扩散系数;A,B为系统控制参量——无尺度的流速度和催化剂的衰变常数[15]。
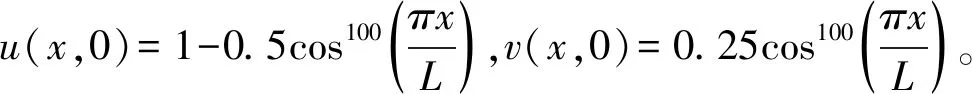

图1 u,v的数值解图,当A=0.01,B=0.1时Fig.1 The plot of solution of u,v at A=0.01,B=0.1
在图2中,取t=4 000,A=0.01,B=0.1,可以看到,2个脉冲每一个都分裂成2个行波脉冲,现在产生了4个脉冲,又过了一段时间,这4个脉冲再一次分裂,此时得到了8个脉冲。这个过程在2个脉冲之外继续,直到填满整个间隔,在这个自我复制的过程中,v在2个峰之间成幅度减小,在脉冲之间u不趋近于1,u的最大值随着2个行波脉冲之间距离的增加而增加。

图2 u,v的数值解图,当A=0.01,B=0.1时Fig.2 The plot of solution of u,v at A=0.01,B=0.1
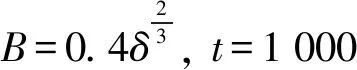
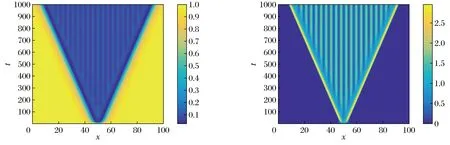
图3 u,v的数值解图,当Fig.3 The plot of solution of u,v at
4 结 论
本文推导了离散余弦变换是如何得到的,通过离散余弦变换的方法对反应扩散方程进行了求解。首先通过考虑区域上有具有齐次Neumann边界的函数u,将求解区域划分为N个网格,取每个网格的中心点得到离散点集。然后根据余弦函数族在点集上的正交性,得到函数u的最小二乘余弦逼近多项式SN。将离散点集代入SN中,可以证明SN(xj)=uj。通过建立映射得到了离散余弦变换,然后应用离散余弦变换得到了关于频域上的常微分方程组,通过向后Euler方法离散时间导数,最后应用Picard迭代求解非线性代数方程组。通过对数值算例的数值结果进行仿真计算,证实了通过离散余弦变换来求解反应扩散方程是有效的,快速的。
