加工时间可控的单机工期分配问题
2019-12-03赵玉芳富晓双
赵玉芳, 田 野, 富晓双
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
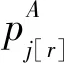
文献[6-8]是近期国内有关加工时间可控的单机排序问题的论文。近年带有资源分配的排序问题也受到更多学者的关注,即通过给工件分配额外资源的方式减少工件加工的时间。SHABTAY和KASPI[9]提出凸资源消耗函数:pj=(wj/uj)k,其中wj为基本加工时间,uj>0为分配给工件Jj的资源量,k是给定的整数。WEI等[10]研究了工件的实际加工时间为关于开始加工时间和资源分配线性函数的单机排序问题。文献[11-16]是关于资源分配相关的文章。高洁等[8]分别研究了带有与工件位置相关的学习效应和与工件开始时间相关的恶化效应的单机排序问题。并对带有资源约束的情况讨论了线性资源分配的单机工期排序问题。WANG等[16]研究了带有资源分配的单机提前延误排序问题。其中工件的加工时间是关于开始时间、资源分配的函数。并证明此问题是多项式可解的。
本文研究了带有学习效应、恶化效应和资源分配的单机工期分配问题。文献[16]从2种不同加工时间函数和3种不同的工期分配方法的角度分析了带有资源分配的单机工期分配模型。本文的不同之处是提出凸性资源分配情况下工件的实际加工时间,表示为:pjr=(pjar-1/uj)c+bt,uj>0。并从CON、SLK及DIF这3种不同的工期分配问题的角度分析。找到最优排序π*,使包含提前、延误、工期、总资源消耗的目标函数最小。并证明这些问题都是多项式时间可解的。
1 问题描述
本文研究带有学习效应、恶化效应及资源分配的单机工期排序问题,模型描述如下:
设有n个工件且在0时刻全部到达,n个工件的集合为J={J1,J2,…,Jn},其中pj表示工件Jj的基本加工时间,dj表示工件Jj的工期。对于任意给定的排序π,研究带有凸性资源分配问题,工件的实际加工时间为
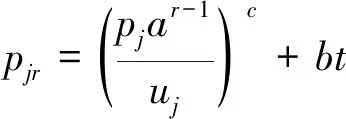
(1)
其中:b表示工件的恶化系数,且b≥0;0
用[j]表示第j个位置的工件;Cj表示工件Jj的完工时间。Ej=max{0,dj-Cj}表示工件Jj提前时间;Tj=max{Cj-dj,0}表示工件Jj延误时间;α、β、γ分别表示工件提前、延误和工期的单位系数,Gj表示单位惩罚加权系数。目标是确定最优排序π*,使目标函数值最优。其中目标函数包含提前、延误、工期、资源分配等,表示为
本文从3种常见的工期分配问题的角度进行研究。3种工期分配问题分别为
1) 公共工期(CON):所有工件都有相同的工期dj=d(j=1,2,…,n),其中d≥0为决策变量;
2) 松弛工期(SLK):dj=pj+q,j=1,2,…,n,其中q≥0为决策变量;
3) 无限制工期(DIF):每个工件都有不同的工期,且工期的分配不受任何限制。
用三参数表示法,本文研究的问题可表示为
2 主要结论
关于CON、SLK及DIF三种工期分配问题,与文献[16]类似,有如下结论:

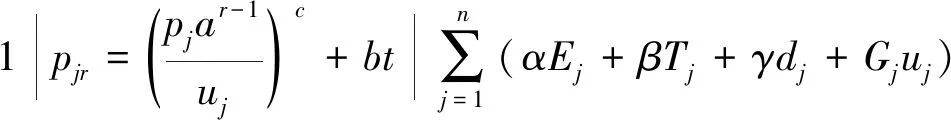

图1 排序π*的甘特图Fig.1 The Gantt chart of sequence π*
1) 对于CON工期,最优工期的值与某个工件的完工时间相同,即d=C[k];
2) 对于SLK工期,决策变量q=C[k-1];
3) 对于DIF工期,如果当γ≥β有dj=0;当γ<β有dj=Cj。
证明 对于CON工期,假设d在第k个工件加工过程中。即d-C[k-1]=δ>0。
此时目标函数为
若记:A=α(k-1)-β(n-k+1)+γn
则f(d,π)=Aδ+B

其中k由下式得到
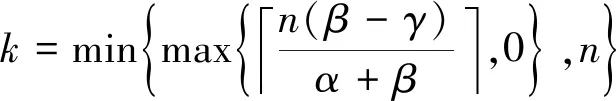
(2)
同理可证SLK及DIF工期。
对于不带资源分配的问题有如下结论:

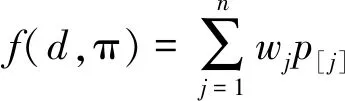
(3)
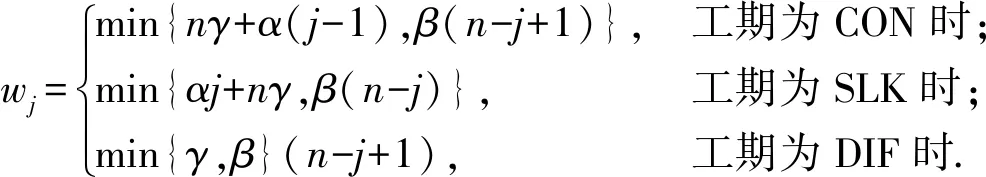

2.1 CON工期
在CON工期分配问题中,所有工件都有相同的工期dj=d(j=1,2,…,n),d≥0,最优工期的值与某个工件的完工时间相同d=C[k],其中k值可由式(2)得到。则前k-1个工件提前;第k个工件恰好在工期时间完成;第k+1个到第n个工件延误。对于任意排序π有
综上,目标函数为
设wj=min{nγ+α(j-1),β(n-j+1)},则
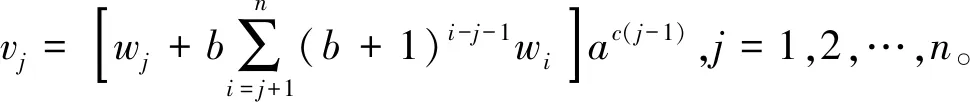
2.2 SLK工期
综上,目标函数为
设wj=min{αj+nγ,β(n-j)},与CON工期推导类似可得
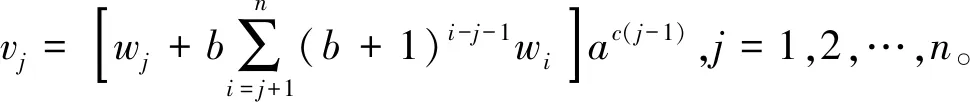
2.3 DIF工期
由引理2可知,对于DIF工期分配问题,在最优排序中,当γ≥β时有dj=0。此时对于任意j,Ej=0,Tj=Cj;当γ<β时有dj=Cj。此时对于任意j,Ej=Cj,Tj=0。综上,目标函数为
设wj=min{γ,β}(n-j+1)。与CON工期推导类似可得
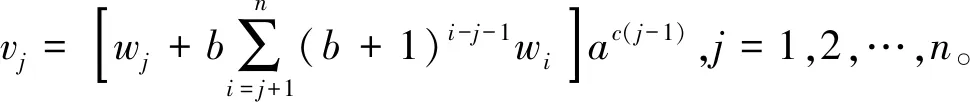
综上,CON、SLK及DIF这3种不同工期分配问题的目标函数表达形式类似。则可以得到以下引理:
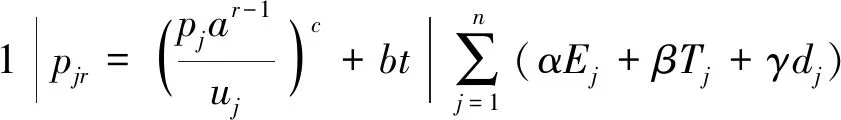
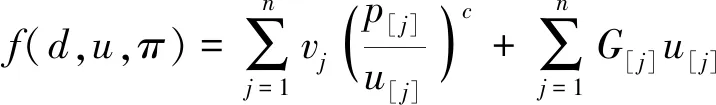
(4)
其中
引理5 对于任意排序π,CON、SLK及DIF这3种不同工期分配问题的最优资源分配均可以写为
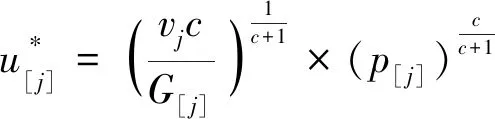
(5)
证明 由式(5)知,对于任意排序π,为了使目标函数最优,需对式(4)求导:
令f′=0有

对于CON、SLK及DIF这3种不同工期分配问题,将式(5)代入式(4)中得到
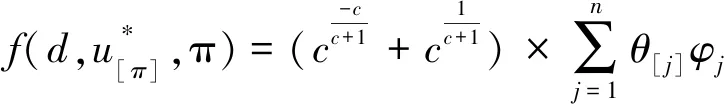
(6)
其中
由式(7)和式(8)知,θ[j]只与工件相关,φj只与位置相关。为了找到3种不同工期分配问题下凸性资源消耗函数的最优排序,需要将位置惩罚φj与工件相关花费θ[j]进行最优匹配:
引理6 3种不同工期分配方法下凸性资源消耗函数的最优排序π*可以通过以下方法得到:位置惩罚φj的最小值与工件相关花费θ[j]的最大值相匹配,位置惩罚φj的第2小的值与工件相关花费θ[j]的第2大的值相匹配,以此类推。
证明 由文献[18]知,2个向量相乘逆序排列时函数值最小
对于该问题可用如下算法求解:
算法
步骤2 由式(7)、式(8)计算φj与θ[j]的值,其中j=1,2,…,n;
步骤3 按位置惩罚φj的值从小到大,相关花费θ[j]的值从大到小的顺序进行匹配。
定理1 算法能在O(nlogn)时间内解决3种不同工期分配方法下凸性资源分配函数的排序问题。
证明 算法中步骤1、2可以在线性时间内执行,步骤3需要用O(nlogn)时间内执行,因此算法的总计算复杂度为O(nlogn)。
3 结 论
本文研究了带有学习效应、恶化效应和资源分配相关的单机工期分配问题。确定了最优排序,使包含提前、延误、工期、总资源消耗的函数最小。证明该问题在O(nlogn)时间内可解。本文仅研究了单机状态下的排序问题,还可将该问题推广至平行机或流水作业等其他复杂的排序问题;或者还可以增加影响工件加工时间的其他因素,比如带有维修的情况。