基于纵横弯曲理论在役测量刚性吊架的工作载荷
2019-12-02黄小波潘万军朱晓锋付勇阙家嘉
黄小波,潘万军,朱晓锋,付勇,阙家嘉
(苏州热工研究院有限公司再制造中心结构强度所,江苏苏州215000)
1 研究背景
管道支吊架是管道系统的重要组成部分,它起着承载管道重量,限制管道位移和控制管道振动的作用。管道设计过程中,要求每个支吊架在不同的工况下承载特定的载荷[1]。但是,在管道及其支吊架的安装过程中,难免会因为制造误差、安装误差及各种因素导致管道的实际运行状态与设计存在偏差。管道支吊架的实际承载载荷与设计载荷之间的偏差无疑是使管道处于不良工作状态的最直接且影响最大的因素。然而,除了弹簧支吊架能够读取具体载荷,其他所有支吊架的工作载荷都无法直接获取。而且在安装过程中,没有相关安装标准要求测量刚性吊架的载荷[2],导致管道安装之后其实际状态与其设
计状态之间存在无法度量的差异。这对管道及设备的运行及寿命都不利。
为了明确在役刚性吊架的具体承载载荷,更加全面地评估和掌控管道系统的运行状态,延长管道及设备的使用寿命,本文以纵横弯曲理论为基础,设计了一种在役测量管道刚性吊架工作载荷的方法。
2 吊杆的纵横弯曲
2.1 轴向拉力和横向剪力共同作用时吊杆的弯曲变形
刚性吊架的吊杆多为细长螺杆,在结构上可以将吊杆视为梁进行计算。传统意义上的结构梁主要承受横向载荷的作用,且在发生弯曲变形时形变量远小于梁的横向尺寸,因此,建立梁的绕曲线微分方程时,不考虑轴向力对梁的弯曲变形的影响。这种简化对结构梁有足够的精度,能满足工程实际的需要。但是由于吊杆比一般结构梁有更大纵横比,当吊杆受到横向载荷作用时,会发生与横向尺寸同等量级甚至更大的位移,并且吊杆主要承受轴向载荷。当把吊杆简化为梁进行计算时,必须考虑轴向力因弯曲变形而产生的弯矩[3]。该类弯曲即称为纵横弯曲。
根据管道刚性吊架的实际情况将吊杆简化为简支梁,吊杆在轴向拉力及横向剪力共同作用下的变形如图1 所示。
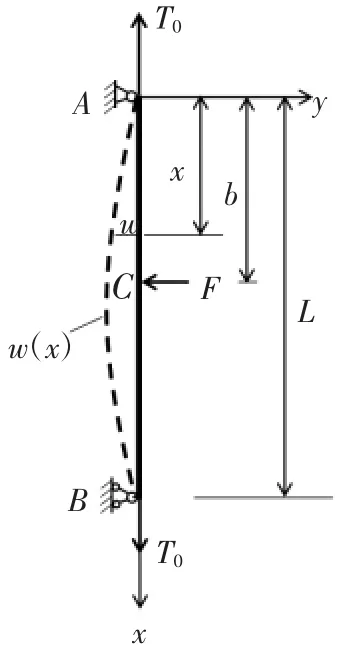
图1 吊杆在横向拉力和轴向剪力共同作用下的变形
假设吊杆材料的弹性模量为E,对应弯曲变形方向的截面惯性矩为I。则相应的弯曲刚度为EI。变形后吊杆的绕曲线微分方程为:
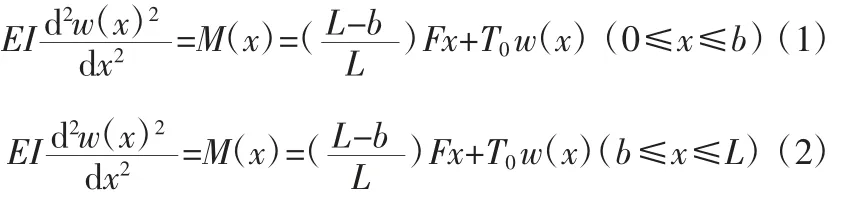
式中,w(x)为绕曲线方程;M(x)为截面x上的弯矩。式(1)和式(2)等号右边第一项表示横向剪力F对截面x产生的弯矩;第二项表示轴向拉力T0对截面x产生的弯矩。由于在图示坐标系下绕曲线w(x)为负值,拉力T0的存在减小了拉杆截面上所受的弯矩;L为杆长;b为剪力F的作用点与杆端的距离。本方法中视吊杆为均匀等截面直杆,弯曲刚度EI为常数,则式(1)和式(2)均为常系数非齐次线性微分方程,规定k2=T0/EI,则其通解为:

式中,A、B、C、D为任意常数,由吊杆的位移边界条件确定,有
w(x=0)=w(x=L)=0。则:

另外,在横向力F作用处的截面x=b上,由式(3)和式(4)
表示的吊杆绕曲线有相同的绕度和转角,从而有:
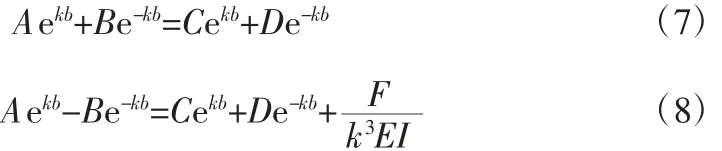
联合上述4 个位移边界条件可以得出A、B、C、D的表达式,从而得到载荷T0和F共同作用下吊杆的绕曲线方程为:

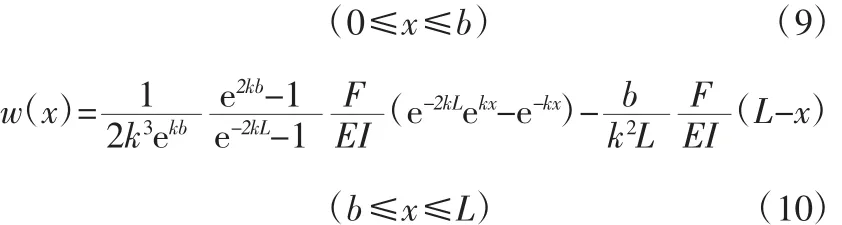
考虑一种特殊情况,将横向剪力F作用于吊杆中点(b=L/2),则此时吊杆的绕曲线方程简化为:

此时,吊杆中点处的挠度为:
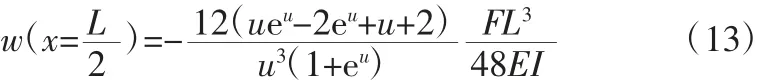
2.2 影响因子及其特性
等式(13)右边第二个因子FL3/48EI表示只有横向力F作用时,吊杆中间位置x=L/2 处的绕度,第一个因子12(ueu-2eu+u+2)/u3(1+eu)除与吊杆的材料参数及几何尺寸有关,只与轴向拉力T0有关,因此,其表示轴向拉力T0对吊杆弯曲变形的影响,将其命名为影响因子并令α=12(ueu-2eu+u+2)/u3(1+eu)。
2.2.1 有界性
F作用时的理论值即理论上当T0趋近于0 时,横向剪力将不能使吊杆产生弯曲变形[4]。
2.2.2 单调性
可以证明,α 在T0∈[0,∞)上单调递减,也即当轴向拉力T0增大时,吊杆将越不容易发生弯曲变形。需要特别指出的是,本文定义的影响因子α 越大意味着轴向拉力T0对吊杆弯曲变形的影响越小,反之亦然。α 的单调性保证了T0与α 的之间的一一对应关系,从而保证了本文设计的载荷测量方法的可行性。给定长度L=2000mm,截面半径D=20mm 及弹性模量E=210 000N/mm2的吊杆,其影响因子α 随轴向拉力T0的变化关系如图2 所示。
3 刚性吊架载荷测量及误差分析
3.1 载荷测量步骤
载荷测量步骤为:(1)对于需要测量的刚性吊架,根据其几何尺寸和材料参数确定出类似图2所示的影响因子随轴向拉力变化的曲线或表格;(2)在吊杆中点处作用横向剪力F使吊杆发生轻微的弯曲变形,记录横向剪力F及作用点的绕度w(x=L/2)。将所得结果代入式(13)计算出此时的影响因子α,进而通过查步骤(1)中所绘制的曲线或表格得到吊杆的载荷。(3)为了得到更加精确的测量值,在横向加载时记录一系列数值,通过拟合得到吊杆的载荷。

图2 特定吊杆影响因子α 随轴向拉力T0 的变化关系
3.2 误差分析
本方法中有很多因素会导致误差,如吊杆几何尺寸的测量、加载载荷的测量以及吊杆挠度的测量等都会有一定的误差,此类误差可以通过采用精密的仪器设备来降低。另一类误差如横向加载时吊杆轴向拉力的变化、吊杆中间连接件的影响以及位移边界条件的简化等是理论模型中没有包含的因素,因此,无法通过精确测量来降低或消除。
3.2.1 横向加载时轴向拉力的变化
刚性吊架吊杆下端与管部连接承载管道重量,在对其进行横向加载的过程中,吊杆轴向位移量与管道向上位移动态平衡。吊杆下端的轴向自由度介于无约束与约束之间,而在理论模型中,假定了吊杆下端为简支约束,即轴向自由度不受约束。因此,实际测量所得的吊杆载荷是已对吊杆横向加载后吊杆所承受的拉力,测量值较实际值偏大。但是测量值介于吊杆下端轴向自由度无约束与被约束时横向加载产生相同挠度时的轴向拉力值之间。
图3 给出了长度L=2000mm,截面直径D=20mm 及弹性模量E=210 000N/mm2的吊杆承受10kN 的轴向拉力,下端轴向自由度分别为无约束和被约束情况下,对其进行横向加载时轴向拉力随吊杆中点横向绕度变化的数值模拟结果。由图3 可知,当吊杆下端轴向自由度无约束时,其轴向拉力不随横向加载而变化。而当吊杆下端轴向自由度被约束时,其轴向拉力随横向加载而增大。当吊杆中间挠度为5mm 时其增量为,当吊杆中间绕度为10mm 时,其增量达到36.1%。尽管刚性吊架的实际情况介于二者之间,但是为了得到精确的测量结果,通常需要通过一系列的取值进行拟合得到吊架的载荷,以此消除横向加载引起轴向载荷变化造成的误差。
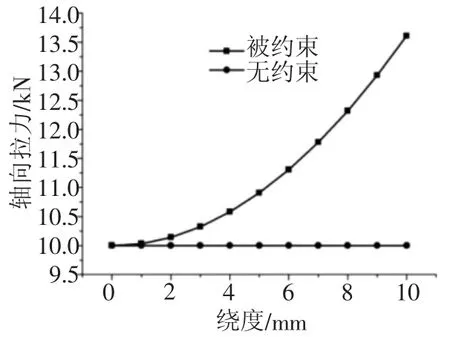
图3 2 种约束状态下轴向拉力随横向绕度的变化
3.2.2 中间连接件的影响
有的刚性吊架为了便于调节而配有花篮螺丝,或者为了延长吊杆而有螺杆连接件等。这些部件的存在往往使其所在位置的抗弯刚度增加,相同横向载荷作用下,实际测得的挠度较理论模型偏小,使采用理论模型计算出来的影响因子偏小,导致测量的结果较实际载荷偏大。对于螺杆连接件和花篮螺丝的长度远小于吊杆长度的刚性吊架,因花篮螺丝和连接件不会对整个吊杆的弯曲刚度引起较大变化且吊杆挠曲线曲率半径足够大,这些部件所产生的误差是可以忽略的。
3.2.3 端部约束的简化
前文讨论了刚性吊架下端简化为简支约束会对轴向拉力测量结果产生误差,这主要是针对吊杆的轴线方向的自由度而言,而对于吊杆端部横向的自由度以及3 个方向的转动自由度约束的简化是否合理,也会使理论与实际产生偏差。理论模型中,吊杆两端均假设为简支约束。实际情况下,吊杆的上、下端往往通过吊耳与管部或钢结构相连,即使与钢结构直接连接时也增设了半球形的垫片使吊杆能够自由转动。因此,将其端部约束简化为简支约束是合理的,不会使测量结果产生较大误差。
4 结论
本文设计了一种刚性吊架载荷的在役测量方法。该方法可以随时测量刚性吊架的工作载荷,解决了管道系统中刚性吊架安装后无法获得其具体承载载荷的难题,使人们更加精确地评估和控制管道系统的运行状态,保证管道系统及设备安全稳定运行的同时延长其使用寿命。本文推导的影响因子以及杆件轴向拉力测量方法不仅适用于刚性吊架,还适用于工程结构中任何承受轴向拉力的杆件的载荷测量,对该类结构的工作状态的评估具有重要意义。
