混流式水轮机径向振动的传递路径分析
2019-12-02职保平秦净净李正星
职保平, 秦净净, 李正星, 于 洋
(1. 小流域水利河南省高校工程技术研究中心,河南 开封 475004;2. 西藏自治区水利电力规划勘测设计研究院,拉萨 850000;3. 国家电投集团云南国际电力投资有限公司伊江建设分公司,云南 腾冲 679100)
水电站厂房结构振动问题复杂,振源间的耦联关系与厂房结构的复杂性是制约其发展的重要因素。目前在振源的解析处理、各结构响应的分析在机理与仿真方面研究成果丰富[1-5],随着技术的发展,有限元法逐步取代了传递矩阵法,但在实际工程中,由于边界条件、物理参数等不确定参数的存在,使有限元计算存在不小的误差,近年来,针对该问题,发展了基于试验和理论分析相结合的振动分析方法[6-7],以及引入随机参数结合实测数据来反演修正仿真结果[8-9]等方法。
在工程结构问题中,结构参数、外荷载的不确定性是客观存在的,目前主要有随机理论、模糊数学和区间分析三种基本方法。其中,由于区间分析只需较少的已知信息(如材料参数的界限、测量信息误差范围等),能够比较客观反映事实,减少了认为因素的影响,提高分析结果的可靠性,而且,得到结果也包含可行解集的一个最小区间集合,为实际工程提供简便。近年来,应用区间分析方法进行结构分析的研究日益受到重视[10]。
随着机组尺寸的增加、支撑刚度的相对降低和运行工况的频繁变化,机组水力、机械和电磁振源之间的耦合作用越来越明显,而目前关于多阵元耦合作用机理及其诱发厂房结构相互作用的问题研究相对滞后,尚缺乏明确的机理表达和完善的研究模型。
本文从约束振动作用的构件为出发点,从振动传递的角度,避开振源之间耦合的机理表达,在竖向研究的基础上[11],展开对更为复杂的径向振动传递规律进行分析,给出各振源通过各导轴承的比例,同时在分析中引入区间参数,一定程度上能够解决简化模型带来的误差问题,从而拟合实际问题,为全面分析水电机组振动传递特性提供理论基础和数据支撑,因此,本文针对径向振动的传递路径分析是十分有必要且有意义的。
1 建立机组-厂房耦联系统数学模型
1.1 径向振动的主要来源
作用在机组轴系上的外力主要有各种不平衡力、导轴承的油膜力和蜗壳、尾水管等处水流的脉动压力,以半伞式机组为例,力的简化模型如图1所示。在这些激振力的作用下,水轮机的振动既是周期的,又是随机的。

图1 半伞式机组旋转轴系-厂房结构受力简化模型Fig.1 Simplified force model of semi-umbrella unit rotating shaft system structure
水电机组厂房结构受到的主要不平衡力有:①由旋转部件质量分布不均匀引起的机械不平衡力;②轴线与法兰不垂直、轴线与推力轴承镜板不垂直或各导轴承间隙不等引起的转子作弓状回旋所产生的不平衡力;③由于转子磁极外圆或定子内腔不圆或转子与定子不同心等,导致转子四周的磁拉力不对称所产生的不平衡磁拉力;④由转轮叶片形状不一致或迷宫间隙发生周期性变化引起的水力不平衡力;⑤在流道内的流体周向不对称,所产生脉动压力载荷;⑥各导轴承内的油膜压力。
以上几种不平衡力是相互作用相互影响,投产的立式水轮发电机组中,约有10%的机组发生过加剧振动,加剧振动的原因约有60%是由水力脉动荷载和旋转体不平衡荷载。
但无论何种机组,何种荷载,最终对机组径向振动主要由上导轴承、下导轴承或者水导轴承来约束。中大型水电机组汇总,各个导轴承多采用多瓦块构成的可倾瓦式滑动轴承,可将导轴承简化为一个弹簧进行处理。表1给出了各个厂房各轴承的典型刚度值[12],根据各个振动分量的理论解,结合各电站分析中所采用的参数,最终可确定参数的扰动范围。

表1 各电站计算中轴承刚度值的设定Tab.1 Bearing stiffness value of power stations
机组的径向振动通过各导轴承传递至混凝土基础,在计算产生各轴承刚度的前提下,可建立数学模型进行简化计算。
1.2 径向振动的传递路径
经过长期的理论研究及实践检验,水电机组厂房结构的径向振动传导主要由以下方式传递:路径①上导~上机架~千斤顶~风罩~厂房;路径②下导~下机架~地脚螺丝~厂房;路径③水导~顶盖~厂房。
三种路径中:路径①是大轴由上导轴承约束所受到的径向力通过上机架传递至千斤顶进一步传递至风罩,最终传递至厂房;路径②是大轴由下导轴承约束所受到的不平衡力由下机架基础地脚螺丝传递至厂房;而机墩由若干个指点,产生相应个方向的作用力组合;路径③是指水导轴承水平作用力通过顶盖系统传递至附近混凝土。
1.3 简化模型的建立
以立式半伞式水轮发电机组为例,其转动部分的径向振动通过导轴承、机架、地脚螺丝传给钢筋混凝土机墩,对机组厂房结构的简化如下:
将大轴看无质量的弹性连续梁,将其质量做附加质量加至轴的三个节点m1,m2,m3处,节点之间的大轴刚度用k1,k2表示。
m1为励磁机转子带轴和1/2大轴顶部至转子支架的轴系质量及其他作用在大轴顶部的质量;m2为转子支架中心体质量、1/2支臂的总质量和1/2整个轴质量;m3为水轮机转轮质量、水导轴承座、水体附加质量和1/2转子支架至水轮机处轴的质量。
m4为上机架靠近大轴处集中质量、1/2上机架支臂及上导轴承座的总质量;上机架与大轴通过上导轴承连接,可将其简化刚度k3;上机架简化为无重力梁,其刚度之和为k4;上机架外端通过千斤顶固定于风罩上,假定千斤顶支撑足够,使上机架与风罩呈刚性连接。
风罩一般为混凝土结构,将其作为等效节点m5考虑,节点质量包含风罩质量及1/2上机架支臂质量,风罩混凝结构的刚度为k5,下部与混凝土基础固结。
由于转子边缘处的磁轭、磁极质量较支臂的质量大得多,故将支臂简化成无质量弹性杆,将其质量平均分配给转子边缘和支架中心体。设全部支臂的刚度之和为k6,转子边缘处的集中质量为m6,简化为单自由度节点。
m7为下机架靠近大轴处集中质量、下导轴承座及1/2支臂的总质量;质量m7通过简化成等效刚度为k7的下导轴承与质量m2连接;下机架支臂简化为无重力梁,其刚度为k8下机架外端刚性固定于混凝土基础上,暂忽略基础的耦联作用;下机架也简化为单自由度节点。
将顶盖上的附加部件作为附加质量考虑,节点m8为顶盖靠近大轴处集中质量、水导轴承座及1/2顶盖系统的总质量,将顶盖系统简化为无重力梁,其刚度为k9,其中,m8通过简化成等效刚度为k10的水导轴承与简化为等效刚度为k11水力密封联立与m3节点相连接。大型机组的尺寸和重量都比较大,为计算方便,对机墩进行简化:蜗壳底部结构假定为刚性基础,而由于蜗壳外围混凝土与机墩之间跨度较大,将机墩至蜗壳顶部之间混凝土做等效节点m9考虑,其刚度为k12,蜗壳顶部至围岩部分的混凝土做等效节点m10考虑,其刚度为k13。机墩结构近似按轴对称计算,蜗壳层取轴对称平均断面处理。简化模型如图2所示。
将轴系、转子、下机架、顶盖、机墩平衡方程归并到一起,扩展后得到总刚度阵为

(1)

图2 半伞式机组径向振动简化模型Fig.2 Radial vibration simplified model of semi-umbrella unit
式中:k10-11为由水导轴承和水力密封联立的结果。阻尼阵与刚度阵类似,质量阵采用集中质量,形成总体质量阵为
M=diag{m1,m2,m3,m4,m5,m6,m7,m8,m9,m10}
(2)

U={u1,u2,u3,u4,u5,u6,u7,u8,u9,u10}F(t)={0,0,F0eiωt,0,0,0,0,0,0,0}
(3)
式中:Ud为U的均值,最终可得系统的动力平衡方程
(-ω2M+iωC+K)U=F(t)
(4)
定义传递率为传递力的幅值与振源的幅值之比
βt=|Ft/F0|
(5)
通过求解不同路径的传递率即可得出振动路径在频域内的梯度排序。
1.4 区间参数化的分析
(6)
则区间变量可表示为x=xc+δx,δx∈ΔxI=[-xr,xr],δx为对称区间变量。区间参数的分析无需已知参数的概率分布等先验知识,区间运算在进行加减运算时,当区间变量为标准化对称区间变量时,加减运算并不会产生区间扩张的问题,但在乘法计算时易造成解的区间扩张,使结果范围扩大,如何求解正确的解区间是目前研究的热点。在实际应用中,应避免使用乘除法进行区间变量的运算。

考虑到参数在小范围内变化,采用摄动法来求解方程
(7)
将含有区间参数的传导函数FaI在a=ac进行Taylor展开,忽略二阶以上分量,参数具有区间数学中的自然区间扩张可得
(8)
式中:符号∘为Hadamard积。根据区间加减法计算定理得
(9)
由区间相等的充要条件有

(10)
该方法在计算中仅运用区间运算中的加法法则,能够一定程度上避免区间扩散的影响。
2 算例分析
以某巨型水电站为例,该水电站采用地下式发电厂房,伞式机组,单机容量为700 MW,进口段蜗壳直径达7.0 m,机组布置图如图3所示,机组与厂房的主要材料属性如表2所示,主要部件的重量、尺寸如表3所示,表中数据由设计图纸与初设报告提供。

表2 机组与厂房主要材料参数Tab.2 Main material parameters of the unit and powerhouse

图3 某水电站机组布置图Fig.3 Layout of the hydropower station
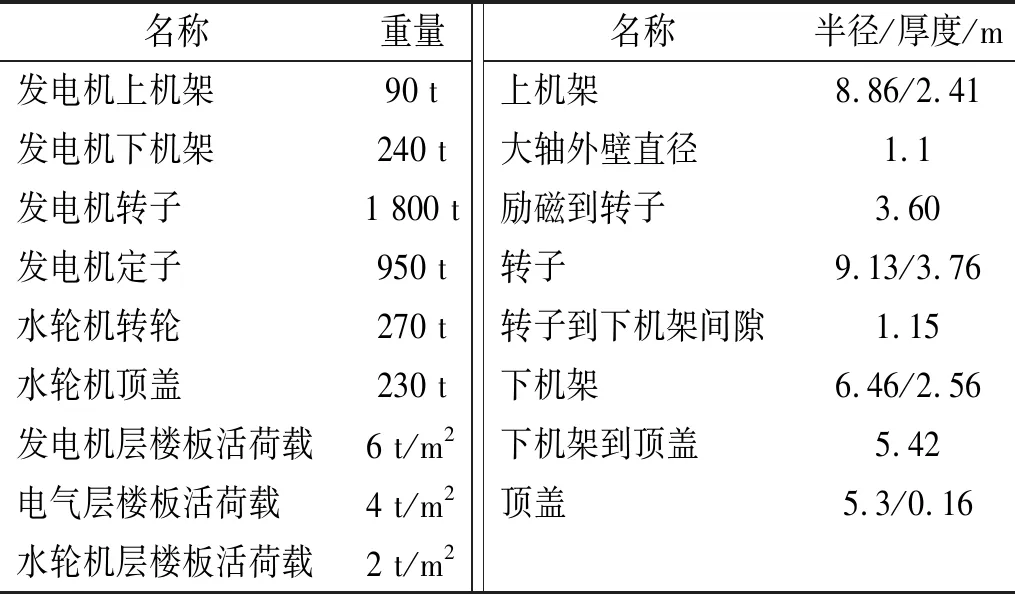
名称重量发电机上机架90 t发电机下机架240 t发电机转子1 800 t发电机定子950 t水轮机转轮270 t水轮机顶盖230 t发电机层楼板活荷载6 t/m2电气层楼板活荷载4 t/m2水轮机层楼板活荷载2 t/m2名称半径/厚度/m上机架8.86/2.41大轴外壁直径1.1励磁到转子3.60转子9.13/3.76转子到下机架间隙1.15下机架6.46/2.56下机架到顶盖5.42顶盖5.3/0.16
各部件的质量由尺寸和材料属性计算得到,等效节点的简化方式按照“2.2”节进行处理,各节点的等效质量见表4。
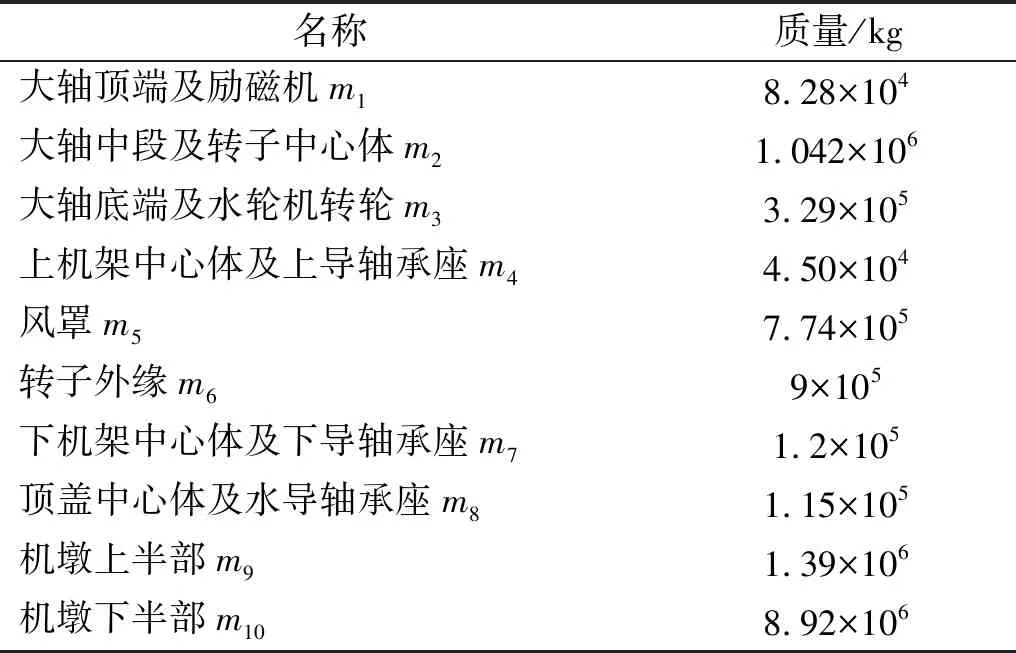
表4 各节点的等效质量Tab.4 The equivalent mass of the nodes
节点等效刚度的计算成果如表5所示。其中,机组大轴、风罩、上机架、下机架、顶盖、机墩等部件的刚度由结构自身特性计算得到,计算仅采用杆单元刚度计算方式进行处理,折减系数为质量参数和图纸计算质量的比值。折减系数的选取及各部件等效刚度、阻尼、质量的计算并不严谨,这是由于本算例仅为传递路径的计算寻找一种方法,数据是否与实际情况严格相等并不在讨论范围内。
各导轴承及密封刚度的选取主要依托于现有、同容量级别工程的公开数据,主要选取原则如下:
上导轴承的等效刚度k3,由单块轴瓦的等效刚度1.36×109N/m进行计算,该电站中上导轴承含16个轴瓦,可计算等效刚度k3=2.176×1010N/m;
下导轴承含36个轴瓦,有效面积25 956 cm2,油量28 000 L,摆幅约束为0.15 mm,可计算等效刚度k7=4.896×1010N/m;
水导轴承单个轴瓦的刚度为1.36×109N/m,本机组水导轴承共含24个轴瓦,可计算等效刚度k11=3.264×1010N/m;
顶盖系统的等效刚度k10主要与顶盖处水封压力和间隙大小有关,但该数据难以得到,在本算例中仅以渔子溪4号机组测试数据为准,即实测大间隙处的水封力为17.3×104N,间隙为1 mm,可计算等效刚度k10=1.73×108N/m。
上述参数中油膜、水封刚度获取较难,且刚度随时间变化,在以往的分析中,导轴承单个轴瓦刚度多取值从2×109~3×109N/m,取值范围较大,因此取k3,k7,k10,k11及其相应的阻尼,参数的区间半径为0.2倍的均值。
结构的等效阻尼采用黏滞阻尼进行计算,其中阻尼比选用0.05。图4~图7给出了各径向不平衡力经过各个路径的传导率排序及传递力的梯度排序。
图4和图7给出了不平衡磁拉力沿上导轴承、下导轴承、水导轴承传递至厂房机墩的传递率排序,并给出了当各导轴承、水力密封参数存在0.2倍均值扰动时,传递率随不平衡力频率变化是的特性曲线。在该模型中,主要是由水导轴承及水力密封进行传递,即在本模型中,由于水导轴承与水力密封联立的路径传导刚度最小,因此传递作用显著高于另外两条路径。

图4 不平衡磁拉力沿各路径的振动传导率及局部放大图Fig.4 The vibration transmissibility and local enlargement of the unbalanced magnetic pull along each path

图5 机械不平衡力沿各路径的振动传导率及放大图Fig.5 The vibration transmissibility and local enlargement of the mechanical unbalance force along each path
图5和图7给出了机械不平衡力沿各导轴承传递至厂房机墩结构的传递率排序,并给出了关键参数存在0.2倍均值扰动时,传递率随不平衡力频率变化是的特性曲线。由转子大轴不对中等产生的工作回旋等所造成的机械不平衡力在三条路径中,仍主要由水导轴承路径传递,相较于不平衡磁拉力的传导过程而言,由于机械不平衡力远离上导轴承约束的路径,路径刚度有一定变化,水导轴承传递率幅度上升,上导轴承传递作用下降。

图6 水力不平衡力沿各路径的振动传导率及放大图Fig.6 The vibration transmissibility and local enlargement of the hydraulic unbalance force along each path

图7 各激励源沿各路径的振动传导百分比Fig.7 Vibration transmission percentage of the each exciting sources
图6和图7给出了水力不平衡力沿各导轴承传递至厂房机墩结构的传递率排序,并给出了关键参数存在0.2倍均值扰动时,传递率随不平衡力频率变化是的特性曲线。由水力脉动产生的水力不平衡力,在三条路径中,主要由水导轴承约束路径进行传递,相较于不平衡磁拉力和机械不平力的传导过程而言,在水力不平衡力的传导过程中,水导轴承及水力密封传递作用进一步提升,扰动作用进一步放大。
3 结 论
多径向激励源在多路径振动传导过程中的特性十分复杂,其机理研究目前尚无定论,本文以振动传导的作用方式来分析各振动源的传播机理,通过算例表明,所提出的分析方法是可行的,在一定条件下能够进行径向振动的激振源的传播方式的分析,确立传递的比例。通过引入参数的扰动性,给出振动特征的取值范围,一定程度上避免了简化所带来的误差,为进一步参数识别提供依据,最终,为水电机组的振动机理研究、安全评价体系建立提供理论支撑。
但在分析中,由于算例简化程度较高,各不平衡力的传导百分比并未随频率发生变化,结构的特性研究较为理想化,其规律较为一致。在实际结构应用时,需提供更为完善的资料、建立详实的有限元矩阵进行分析,并加载时程激励数据,这也是下一步工作的内容,同时,径向振动分析方法中,未考虑结构的扭转振动,竖向振动与径向振动并未联立分析,这也是需要深入研究的内容。
