基于Weibull分布的岸桥铰点退化特征提取方法研究
2019-12-02侯美慧孙德建
侯美慧, 胡 雄, 王 冰, 孙德建
( 上海海事大学 物流工程学院, 上海 201306)
岸边集装箱起重机,简称岸桥,是码头进行集装箱装卸作业的重型起重机械[1]。岸桥金属结构及铰点位置如图1所示。岸桥结构主要由前后两片门框、拉杆和桥架组成。小车轨道一般由铺设在前后大梁上的两条长轨和接轨处的两条短轨组成[2]。大梁铰点[3]既是岸桥整体钢结构的一个动铰,又是小车轨道的支撑结构。在频繁的循环作业中,小车轨道持续承受着复杂的交变载荷[4]和起制动惯性力,轨道铰点处也会承受剧烈的冲击,在长时间的作用下,轨道铰点会产生松动甚至变形,影响小车系统的安全运行。轨道铰点处的振动监测信号蕴含着丰富的健康状态信息,分析并挖掘[5]其中的退化特征信息,能够有助于了解铰点的性能退化状态,从而提高岸桥的运行可靠性。
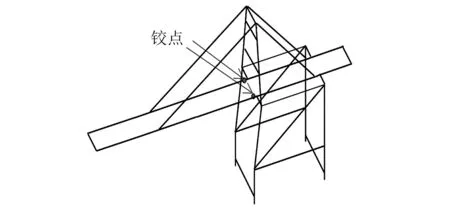
图1 岸桥铰点示意图Fig.1 STS crane turning point
性能退化特征能够将性能退化规律实现参数化,近年来已在轴承、液压泵的研究中取得了一定的进展,实现了对退化状态的识别。刘鹏等[6]提取的形态梯度谱熵作为退化特征能有效的反映滚动轴承的性能退化趋势。王冰等[7]利用GG聚类模糊方法实现了对性能退化状态的识别。田再克等[8]基于改进的MF-DFA方法实现了液压泵性能退化特征的提取。由于岸桥运行工况复杂,现场试验难度大,因此,当前针对岸桥铰点开展退化特征研究的文献相对较少。该对象的研究热点集中在铰点结构的改良以及ANSYS建模上。邓传月等[9]应用小波包方法研究了轨道铰点的机械性能特征参数的统计特征,提取出了不同频段的特征参数,以此作为不同工况的特征参数。
轨道铰点振动信号具有典型的非平稳、非线性、随机性特性。从统计分布理论分析其退化特征,是一条有效的途径。在常见的统计分布模型中,Weibull分布模型由Weibull提出,是一种典型的机械零部件可靠性的分布模型,在寿命预测领域得到了成功的应用。陈昌等[10]将Weibull分布与最小二乘支持向量机相结合应用到滚动轴承的退化趋势预测中,充分发挥了Weibull分布形状参数在早期故障敏感度及粒子群优化的最小二乘支持向量机预测模型优势,预测精度较高。陈光宇等[11]将Weibull分布应用到系统全寿命周期成本建模与决策中,表明了该方法在工程应用上的实效性,为系统工程师开展可靠性设计优化提供了系统的思路和方法。魏艳华等[12]将Weibull分布与贝叶斯估计相结合对混合Gibbs算法给出的数据进行估计,有效的证明了混合Gibbs算法的广泛适应性、可行性、稳定性、有效性。
综上所述,本文针对铰点性能退化特征提取问题展开研究,提出一种基于Weibull分布的铰点退化特征提取方法。首先对数据进行预处理并采用局部最小值法滤除本底噪声,之后对去噪后的数据建立Weibull分布模型,提取其尺度参数和形状参数,并通过VMD(Variational Mode Decomposition)算法提取出参数的趋势项,以此作为评估铰点健康状态的特征参数。
1 基本理论
1.1 Weibull分布
Weibull分布的概率密度函数[13-14]可表示为
(1)
式中:α为形状参数;β为尺度参数;γ为位置参数。
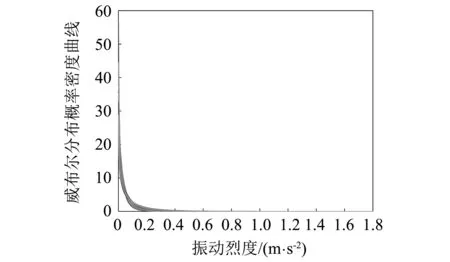
Weibull分布的概率密度曲线如图2所示。可以看出,曲线的形状随着形状参数α的变化而变化,α的改变对分布曲线形式有很大影响。形状参数决定分布密度曲线的形状,当α不同时,其曲线的形状也不同。
当0<α<1时,分布密度为x的减函数;当α=1时,分布呈指数型;当α>1时,密度曲线成单峰分布形式,峰值随α的增大而减小;当α=2时,称为瑞利分布;当α=3.5时,Weibull分布实际已经很接近正态分布了。形状参数值越大,Weibull分布概率密度函数的峰值越大,图形越陡峭。尺度参数β不影响分布的形状,起缩小和放大横坐标尺度的作用,决定曲线放大与缩小比例常数的大小。尺度参数值越大,分布的密度曲线越平缓。位置参数决定分布曲线在坐标系里的起点位置,使曲线在横轴方向左右移动,不影响曲线形状。
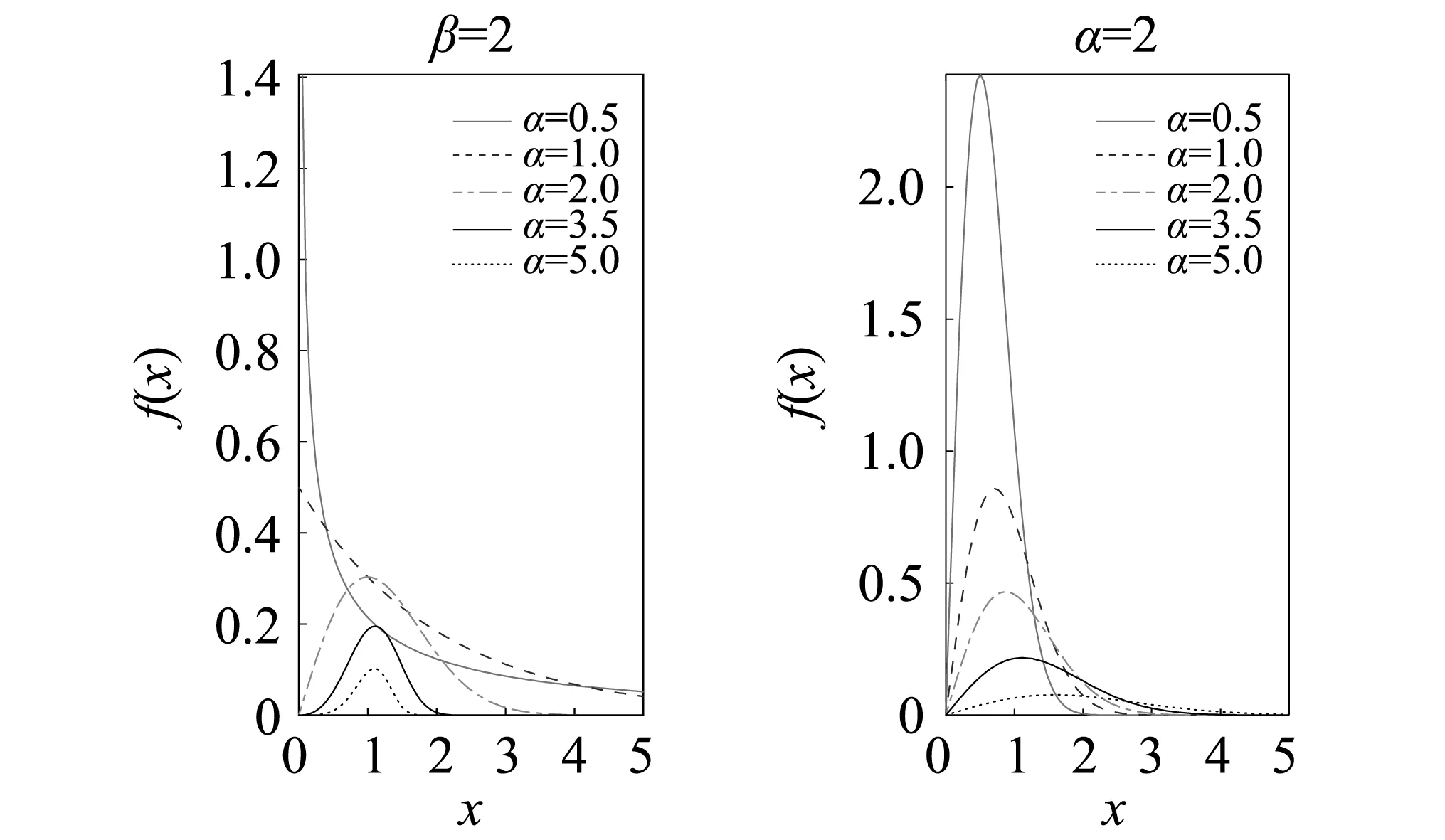
图2 Weibull分布密度曲线Fig.2 Weibull distribution density curve
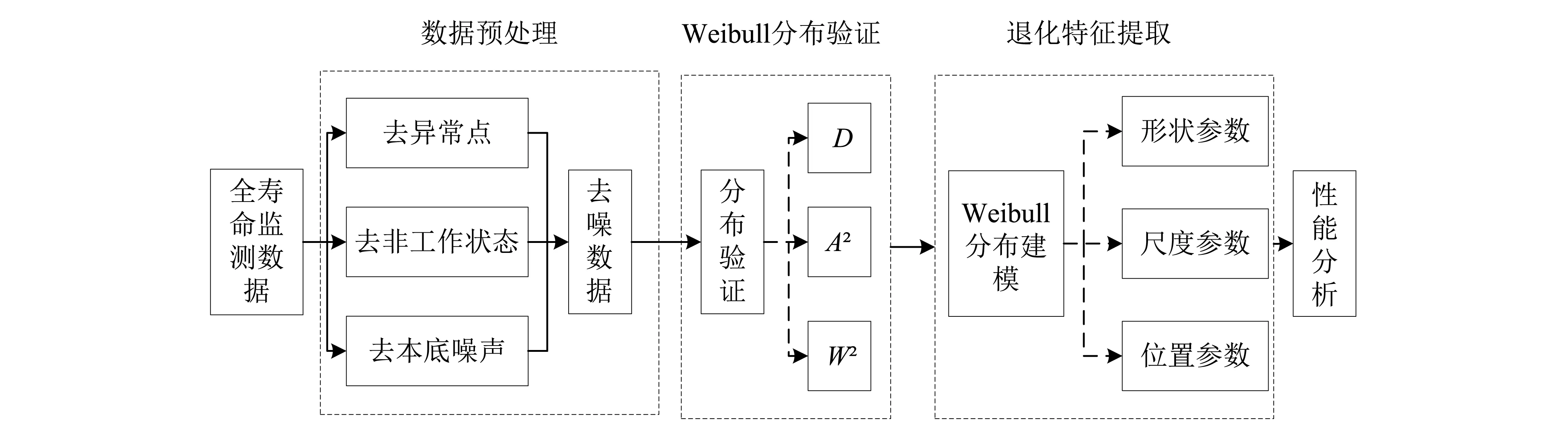
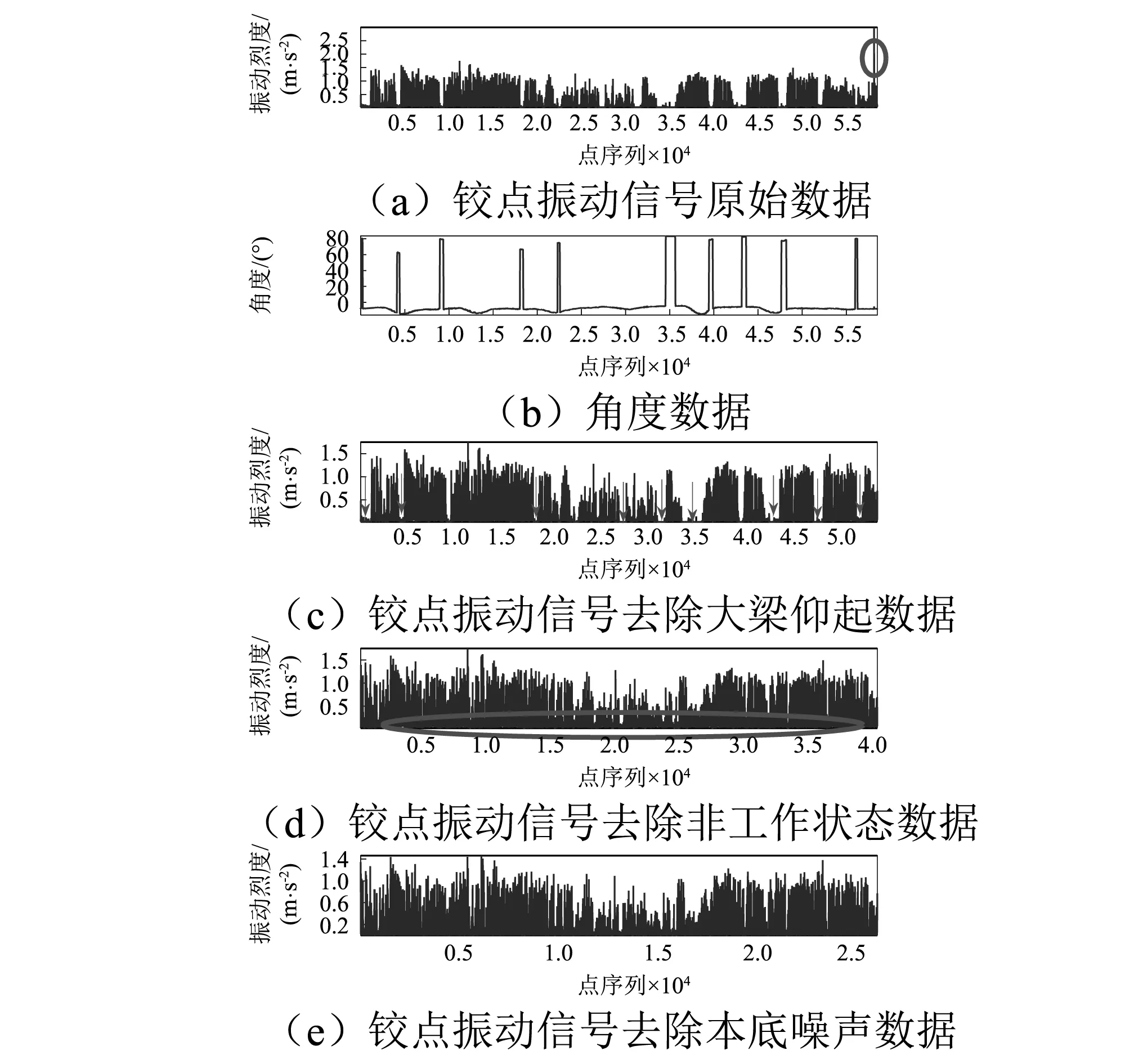
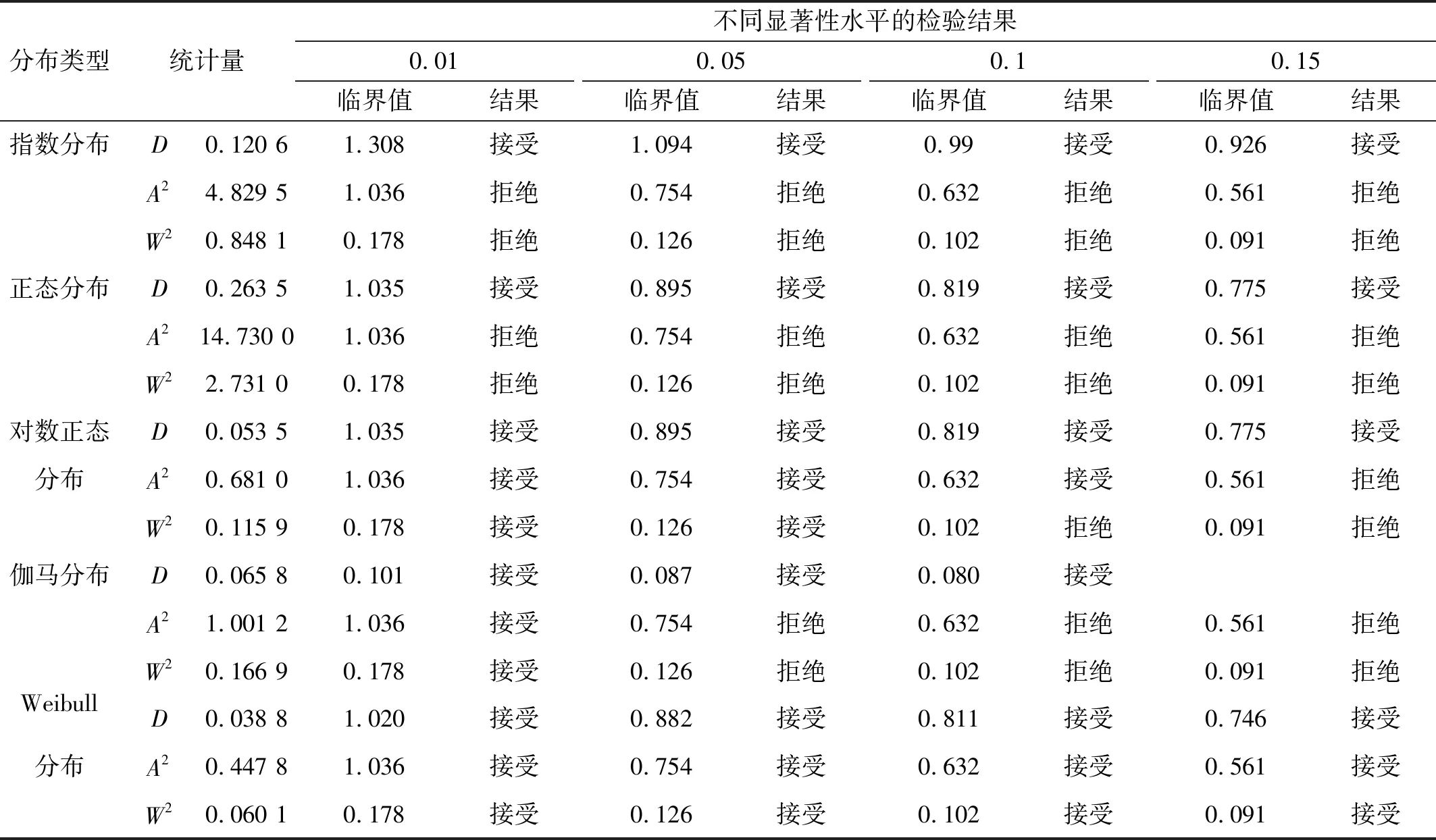
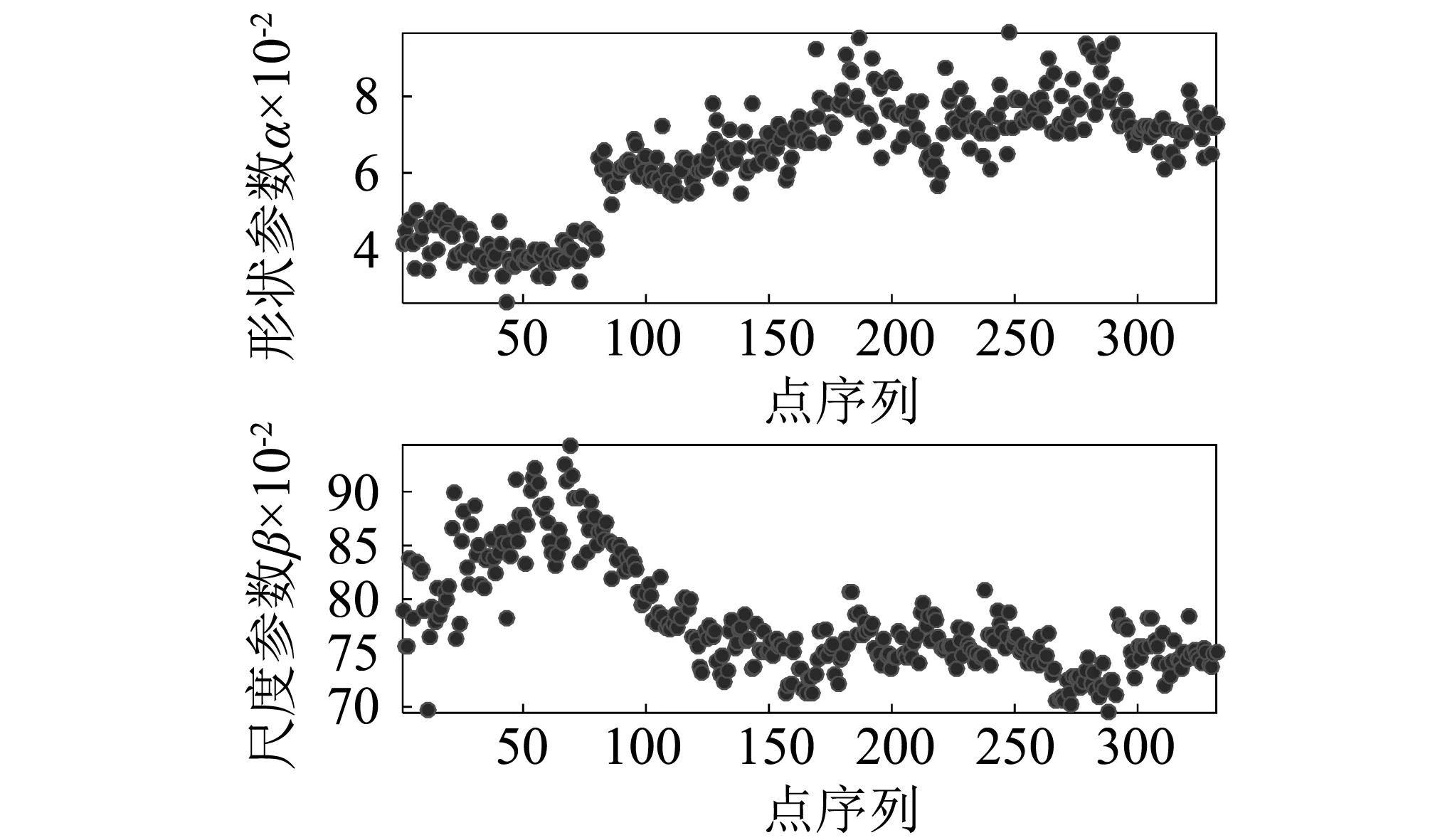
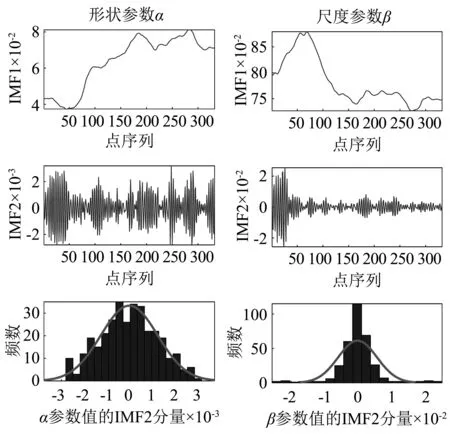
根据给出的Weibull概率密度函数f(x),可以求出变量的分布函数F(xp),即xξ小于某一数值xp的概率P(xξ (2) 该积分表示在0和xp之间曲线与横坐标所包围的面积,通过积分得 (3) 将式(3)的xp用任意的x代替,则可得到Weibull分布函数 (4) 设样本容量为n的随机变量X[15],将样本以升序排列构成顺序统计量x(1) (5) EDF统计量是基于经验分布函Fn(x)构造的统计量,主要描述理论分布函数F(x,θ)与经验分布函Fn(x)之间的差异,通常用两者间的距离来描述,而不同距离的构造方式将得到不同的EDF统计量。Kolmogorov-Smirnov统计量即上确界型统计量D统计量,是按一致距离建立的统计量。Cramer-von Mises统计量即均方型统计量,是以L2距离建立的统计量,包括平方差型统计量A2统计量和W2统计量。 样本容量为n的上确界型统计量Dn为 (6) 式中:∀x为任意x;R为x的定义域。 样本容量为n的平方差型统计量为 (7) 令zi=F(xi,θ),将式(6) 、式(7) 进行积分变换后可得其数值计算公式 (8) (9) (10) 用数值计算的方法根据式(8)、式(9)、式(10)可以计算出统计量D,A2,W2。将D,A2,W2与不同显著性水平下各种假定分布的临界值[16]进行对比,若统计量D,A2,W2的计算值小于临界值,则接受原概率分布假设; 否则拒绝原假设,认为该样本数据不符合原假设的分布模型。 基于岸桥铰点振动信号非线性、非平稳的特点,提出一种基于Weibull分布的岸桥铰点退化特征提取方法。考虑到岸桥实际工况复杂,非工况状态以及噪声干扰严重,首先对数据进行预处理。然后对处理后的数据进行Weibull分布建模,提取分布的形状参数和尺度参数,以此作为性能退化特征。该算法的具体流程如图3所示。 按照图3所示的基本流程,具体的特征提取算法如下: 假设输入信号为X={x1,x2,…,xn},其中n是信号的长度,基于Weibull分布的岸桥铰点振动信号退化特征提取方法的具体实现步骤如下: 图3 基于Weibull分布的退化特征向量提取流程Fig.3 Degradation feature extraction flow using Weibull distribution 步骤1去除异常数据。有些数据明显的较大或者不符合实际情况的,需要剔除,否则就无法有效的获取数据中所蕴含的有效信息。 步骤2去除非工作状态。首先根据大梁俯仰角度的值区分工作状态和非工作状态,当大梁仰起时属于非工作状态,根据角度数据去除该部分数据。但是有时大梁水平岸桥也处于非工作状态,则需要用特殊的方法区分。如振动信号,非作业状态时振动的波动整体非常小,但也会夹杂着一些大的波动,根据这个特点区分大梁水平时的非工作状态。 步骤3去除本底噪声。在本文中本底噪声是指岸桥振动载荷谱信号出现的接近于地毯值的噪声信号。本底噪声产生的原因是由于周围环境中其他机构运行的影响,它的存在主要干扰了振动信号,对其幅值造成一定的偏差,本文应用局部最小值法去除本底噪声。本底噪声具有随机性和可变性,它的大小不能确定,将振动信号细分成若干微小信号段,由于此微段中信号的变化可以忽略不计,可以将本底噪声看成是等大小的。使用局部最小值法的最突出优点是,它可以根据数据特点选择划分长度Δp,且方法较简单。 步骤4Weibull分布验证。根据EDF统计量D,A2,W2的计算值,验证数据的统计分布规律符合Weibull分布。 步骤5退化特征提取。将去噪后的振动数据进行Weibull分布建模,得到形状参数α、尺度参数β、位置参数γ。将得到的尺度参数和形状参数分别进行VMD分解,分解出尺度参数和形状参数的趋势项分量。根据参数的趋势项,评估铰点健康状态。 采用铰点全寿命振动监测数据进行实例分析。该数据来自课题组网络型起重机状态监评系统(NetCMAS)长期在线监测采集的岸桥铰点数据,监测对象为某集装箱码头#8114岸桥。NetCMAS系统主界面如图4所示。振动传感器安装于大梁两侧铰接区域,传感器类型为608A振动加速度传感器。安装方向为V向,如图5所示。信号采样频率2 500 Hz,采样时间0.8 s,采样间隔为8 s。记录得到振动加速度的有效值,并实时存储。 图4 NetCMAS系统界面Fig.4 NetCMAS system interface 图5 传感器安装位置Fig.5 Sensor installation position 按照预处理流程对岸桥振动原始信号进行预处理。 (1)滤除非工作状态 异常点,如图6(a)所示,圆圈中的数据明显跟其它数据不符,为异常点,剔除。然后根据图6(b)角度数据去非工作状态数据,得到如图6(c)所示数据。其次根据非作业状态时振动的波动整体非常的小的特点再次提取出工作状态数据,图6(c)中箭头所指的数据可以看出是岸桥非工作状态的数据,在寻找铰点振动信号的分布规律时应该去掉,得到如图6(d)所示数据。 (2)滤除本地噪声 本文应用局部最小值法去除本底噪声,结果如图6(e)所示。 图6 数据处理过程图Fig.6 Data processing 为了验证试验数据的分布符合Weibull分布。选取某周的岸桥铰点振动载荷为样本,为了保证统计量的渐近有效性,未知参数矢量θ采用极大似然估计。将预处理后的铰点振动数据由式(8)~式(10) 计算出统计量D,A2,W2的值。由表1检验结果表明Weibull分布作为岸桥铰点载荷分布模型较好。 按照上述方法对监测得到的332组数据进行Weibull分布拟合,得到的Weibull分布概率密度曲线如图7所示,得到的尺度参数和形状参数变化趋势如图8所示。可以看出,尺度和形状参数呈现一定的变化趋势,但仍然存在一定的随机波动性。 图7 岸桥铰点Weibull分布拟合Fig.7 STS crane turning point Weibull distribution fitting 表1 岸桥铰点振动载荷5种分布条件下的EDF统计量检验结果Tab.1 The tested results of STS crane turning point vibration load EDF statistics under the condition of five kinds of distribution 图8 尺度参数和形状参数变化趋势Fig.8 Scale and shape parameters trend 为了提取尺度参数与形状参数的主趋势,采用变分模态分解方法[17](VMD)对参数趋势进行处理,经过多次实验分析,本文设置分解层数为2。图9显示了VMD分解的效果图,可以看出,IMF1能够较好地体现尺度参数和形状参数的趋势项。因此,分别采用两个参数的IMF1分量作为描述铰点健康状态的退化特征。以IMF2做频数分布图,并采用正态分布拟合,发现数据符合正态分布。 分析图9中的IMF1变化趋势可以看出,形状参数α在1~50组时呈现减小的趋势,而后在50~184组呈现逐渐增大的趋势,并在184组取得最大值,之后在185~210组逐渐减小后又从211组逐渐增大,到达284组时取得最大值,之后逐渐减小并保持平稳。经检查发现,184组所对应的时间,轨道铰点处已经发生了磨损,钢垫板厚度减小。由于大型的整改对于港口的集装箱装卸量有很大的影响,只是对小车进行了局部调整后继续投入工作,调整之后的铰点数据信号也有了一定的好转。但从211组开始,形状参数α稳步增加,在284组时,经检查发现,小车轨道有了严重的磨损,停工检修时发现钢垫片已经被磨损的只剩几毫米,如图10所示,上轨道也已经形成了不可修复的损伤。更换钢垫片后,其形状参数α逐渐减小并保持平稳。 图9 参数趋势项提取Fig.9 Extract the parameter trend 图10 磨损的钢垫片Fig.10 Worn steel gasket 岸桥整机的机械性能对港口的装卸量有很大的影响,其不可修复的损伤对于整机的寿命有很大的影响。通过对岸桥#8114铰点振动信号从好到坏的全寿命数据的Weibull分布建模,根据参数的变化找到评估铰点健康状态的依据,可以有效的避免轨道发生不可修复的损伤。根据形状参数α的发展趋势,对岸桥铰点的振动状态进行健康评估。通过图9可知,当岸桥处于磨合期时,形状参数α呈现逐渐降低的趋势;当处于正常工作状态时,形状参数α呈现平稳或者逐渐增加的趋势。当形状参数α的发展趋势出现波峰时,要及时对轨道进行修整,避免发生不可修复的损伤。对于大型机械来说,某些故障的发生并不是突发性的,有些故障发生后,还是可以继续运作,但是带伤运作的机械往往带来的是不可预估的危险。 (1)基于岸桥工况的复杂性,提取岸桥铰点工作状态时的数据更有利于统计分析其分布特征。采用局部最小值法可以有效的去除岸桥铰点振动载荷数据的本底噪声。 (2)通过EDF统计量,发现Weibull分布假设能很好地符合岸桥#8114铰点振动载荷的分布特征。 (3)Weibull分布尺度参数和形状参数的变化趋势可以有效的对岸桥铰点的状态进行预警评价。岸桥铰点处于磨合期时,尺度参数呈现减小的趋势;岸桥铰点处于正常工作状态时,尺度参数呈现平稳或者逐渐增加的趋势;岸桥铰点出现故障时,尺度参数会出现波峰。1.2 EDF统计量
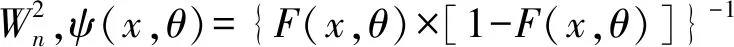
2 基于Weibull分布的铰点退化特征提取
3 实例分析
3.1 数据采集


3.2 数据预处理
3.3 Weibull分布验证
3.4 退化特征提取

4 结 论
