建设高职数学“金课”教学探索
2019-11-30靳娜王小燕
靳娜 王小燕


摘 要:为构建全员、全程、全课程的“三全”育人体系,教育部提出要高校拒绝“水课”,打造“两性一度”的高校优质课堂。建设有深度、有难度、有挑战的“金课”越来越受到重视。对于高职教育领域“金课”也同样受到极大的关注。尤其是高职教育的数学课程,学生不爱学应付了事,老师苦口婆心教不会,教学循规蹈矩,按部就班,缺乏创新。为了改变高职院校数学学习现状,将有丰富内涵的“金课”引入到高职数学课堂迫在眉睫。教师要从课前、课中、课后3个方面做足功课,通过“线上”“线下”互动实现兼顾深度难度,打造丰富有趣,有思考有创新的“金课”。
关键词:高职数学 教学改革 “金课”
中图分类号:G712 文獻标识码:A 文章编号:1672-3791(2019)09(c)-0077-02
日前,教育部发布《关于职业院校专业人才培养方案制订与实施工作的指导意见》。《意见》表明职业院校要推进教师、教材、教法改革,充分利用案例教学,情景教学等教学方式,加强课堂教学管理,广泛运用启发式、探究式、讨论式、参与式等教学方法规范教学秩序,推广翻转式、混合式教学等新型教学模式,推动课堂教学革命,打造优质课堂。随后,教育部高等教育提出“建设中国金课”。至此,“消灭水课、打造金课”已成为高等教育界共识,如何打造高职“金课”,已成为高等职业教育界关注的焦点[1]。目前中国高职教育存在教风怠惰、学风散漫,打造高职“金课”就要充分重视课堂教学,努力营造课堂教学氛围提高课堂教学效率[2]。
数学作为一门基础学科,不仅是高职生学习专业技能的基石,也是学生继续教育,终身学习的基础。同时,数学是提高学生科学素养的一门重要课程,学习数学能够提高学生发现问题、分析问题和解决问题的能力,对学生形成理性思维有着极大的帮助。就目前高职院校中的数学教学出现了诸如教师教学困难,学生学习兴趣较低,整体课堂教学效率不高等突出问题。要想改变这种低效率的课堂教学局面,只有在教学过程中应用科技发展红利,引入现代信息技术教学手段,充分了解学生学习规律和教学规律,贴近生活实际,增加学生的学习兴趣,使学生意识到数学学习的重要性,从而提高课堂教学效率[3]。
为了打造高职数学“金课”,实现“两性一度”的金课标准,就要适应学生自身特点,重视学生“最近发展区”,不能反复教授旧知,亦不能拔苗助长,因此数学教师就要全身心投入,从课前备课预习直到课后检查巩固,一定要竭尽全力,下足功夫精心准备。圆锥曲线的概念教学就应当重视概念形成过程与概念的发展应用,只有学生深入理解概念才能做到应用自如。
1 教学案例
以五年制高等职业教育规划教材数学科目中第九章《圆锥曲线》中《椭圆及其标准方程》为例,该节知识是解析几何里面比较典型的例子,学生要借助平面直角坐标系利用点的运动轨迹思想和代数运算工具来解决几何问题。课程设置的教学目标是要求学生了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用;经历从具体情境中抽象出圆锥曲线中椭圆模型的过程,掌握掌握椭圆的定义、标准方程特点。通过椭圆与其标准方程的学习,进一步体会数形结合思想,锻炼学生的逻辑思维能力和实际动手能力。
1.1 课前准备
课前教师要查阅课程相关资料,整理出有利于教学目标实现的历史素材,案例和学生感兴趣的话题,必要时要学习和制作教学动画。学起源于疑,为提高学生对圆锥曲线知识的学习热情,要求学生分组收集关于圆锥曲线知识的资料,如:
(1)学习圆锥曲线的背景和意义以及圆锥曲线的发展过程。
(2)该文要学习几种圆锥曲线图形。
(3)用绘图工具绘制一个带有椭圆形状的班级logo。
学生通过上网进行有目标、高效率的预习,明确了与圆锥曲线有关的历史背景、数学人物、椭圆的实践意义,增强了学生学习椭圆的兴趣,学生更深刻地了解学习椭圆的必要性和重要性。
1.2 课堂教学
1.2.1 情景引入
教师先考查学生预习情况,做出评价并且介绍该节课的知识背景。为了抓住学生的兴趣点,提高学生注意力,调动学生的主动参与和思考,教师要用多媒体展示宇宙中行星运行轨迹、奥林匹克公园的鸟巢俯视图等。
目的:通过介绍圆锥曲线的历史背景(如古希腊、梅内克缪斯)、太空星球运动轨迹(如开普勒第一定律),让学生了解数学发展对科技进步的重要意义,深刻感受到数学的美妙,体验探索发现的快乐,产生热爱数学、热爱科学的情感。从而引导学生关注我国航天事业的发展历史、卫星发射的重要意义,用视频、图像、数据来展现数学进步与科技发展,数据化时代与人类生活密不可分,息息相关。
1.2.2 探索新知
(1)要求学生通过预习每人画出一组曲线或者由椭圆图形组成的图形。
目的:学生会发现他们画出的椭圆有横着的,有竖着的,而组合的图形又是千变万化。这样既活跃了课堂的气氛又让学生的想象力得到释放。
(2)启发式提问,让学生进一步思考探究。
问题一:同学们画出的椭圆尽管形状不相同但是都有共同特点,那么如何用数学语言来统一概括椭圆的定义呢?
问题二:同学们学过圆的定义,圆是平面内动点到一个定点的距离相等的点的集合,那么形成的椭圆动点是和几个定点之间有关?
(3)问题驱动,用动画演示椭圆轨迹形成。
学生可以观察到一个动点A和两个定F1,F2点之间存在一种等量关系。经过仔细观察和思考可以得出这种关系就是|AF1|+|AF2|=2α(定长)从而得出椭圆的一般定义:平面内到两个定点F1,F2的距离之和等于定长2α(α﹥0)的点的轨迹是椭圆。
(4)探究式提问,引起更深层次思考
问题一:逐渐缩小两定点F1,F2间的距离,直至两定点重合图形会有什么变化?
问题二:若2α=|F1F2|,2α﹥|F1F2|,2α﹤|F1F2|图形会怎样变化?
通过演示提问,学生对椭圆定义有了深刻的理解,明白限定条件(定长2α,定距离|F1F2|)对于椭圆定义意义重大,从而体会到数学语言的严谨和准确,对学生思维的缜密性进行了训练。
1.2.3 体验转化、类比的思维方式
(1)在学习曲线方程的基础上,建立适当的直角坐标系是解决问题的关键。以过定点F1、F2,的直线为x轴,线段F1,F2的垂直平分线为y轴的直角坐标系是较简单的一种。设椭圆上任意一动点M(x,y),由椭圆定义带入条件等式后得到。如何去运算简化公式,是学生遇到的第一个难题,学生的计算能力有限,会花费很大力气,教师引导学生为了化难为易就需要进行移项处理,将代数式转化为。学生遇到的第二个难题是到这一步。教师要引导学生引入新的参数b,将代数式b2=α2-c2带入再进行简化最后得到的标准方程。经过由难到易的代数式转化和引入新的参数,学生体会到遇事要先进行假设和周密的考虑,必要时要转换新思维把复杂问题简单化,不能因循守旧。
(2)得到椭圆标准方程之后,通过前面探究椭圆概念过程的铺垫,学生很容易理解焦点分别在x轴和y轴,两种椭圆图形,就会相对应有两个标准方程,即:和。那么如何根据标准式去判断椭圆焦点的位置。通过观察和指导,学生很快会发现并掌握判断椭圆焦点所在位置的方法。
1.2.4 随堂检测效果
教师在准备好的习题里面,将整理好的有针对性和目的性的练习题发给学生,学生可以利用手机端进行课堂自测,自测提交答案以后,教师可以第一时间统计出错题率。这样既丰富了课堂教学形式也给学生带来新的学习体验,又可以让学生享受科技发展带来的福利,手机也是很好的学习工具。
1.3 课后巩固
课后教师要给学生布置与该节知识点相对应的习题,和通过该节内容来解决实际问题或以提升能力为目的的练习。
所以习题可以分为以下3个层次。
第一层次,必会题型。针对全班同学,尤其是基础差的同学也要求会做。如:
(1)求动点M到定點F1(0,4),F2(0,-4)的距离之和是12的轨迹方程。
(2)求椭圆5x2+6y2=30的焦点坐标,实轴长和虚轴长。
第二层次,基础典型题。学生需要进行判断和思考,有一定数学基础,逻辑思维清析,语言组织能力强,如:
(1)已知椭圆的一个顶点坐标是(3,0),长轴是短轴的3倍,求椭圆标准方程。
(2)已知椭圆焦点坐标是(0,10),求椭圆标准方程。
第三层次,研究性题目。如:
(1)求中心在原点,一个焦点在直线3x-4y+12=0上的椭圆标准方程。
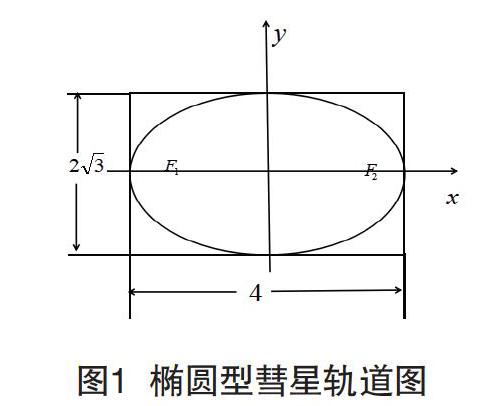
(2)如图1所示,有一副椭圆型彗星轨道图,长4cm,高cm,已知o为椭圆中心,A1、A2是长轴两端点,太阳位于椭圆的左焦点F1处,建立适当的坐标系写出椭圆方程,并求出当彗星运行到太阳正上方时二者在图上的距离。
通过课后3个层次的练习思考,学生对圆锥曲线的认识更加深刻,知识掌握情况较好。这种分层次教学应用于不同学生,起到了有教无类、量体裁衣的效果,使学生对自己学习数学的自信心得到加强。
2 结语
总之,高职数学基础课程在明确学生的知识、能力和素质要求的前提下要注重学用相长、知行合一,引导学生自我管理、主动学习,提高学习效率,着力培养学生的创新精神和实践能力。打造高职数学“金课”,对数学教育提出了更高的要求和挑战,数学教育要培养学生解题途径的思维方式和思维品质,从而进一步潜移默化地影响学生对数学的认识和情感,从这个意义上讲,好的数学教育就是学生学习的资源和动力,“金课”能否代替“水课”,就看学习资源提供的学习价值如何。如果每一堂课的教学设计中融入更多的智慧和创造,数学教育质量就越高,学生的学习资源就越丰富,就越对学生的能力发展有益。
参考文献
[1] 侯长林.应用型高校打造“金课”要体现“七性”[J].职教论坛,2019(3):58-59.
[2] 忻叶.从“水课”到“金课”[J].江苏教育,2019(4):1.
[3] 叶春暖.浅谈激发中职学生数学学习动机的教学策略[J].教育界,2018(35):42-43.
[4] 梁栋,朱鸿玲.数学概念二次教学的实践与思考[J].数学教育学报,2015,2(24):86-87.
