圆幂定理所蕴含的数学思想
2019-11-30王欢欢
王欢欢
【摘要】数学思想在教学过程中的渗透有利于锻炼学生的逻辑思维与创造性思维.圆幂定理揭示了过同一点的弦,切线及割线之间存在的比例关系.本文主要探讨圆幂定理在中学平面几何运用中的三类数学思想,旨在对圆幂定理的教学提供一些参考.
【关键词】圆幂定理;数学思想;统一性
数学思想是对数学知识、理论、方法和规律性的本质认识,是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观点,它在认识活动中被反复运用,带有普遍指导意义,是建立数学和运用数学解决问题的指导思想.常见的数学思想有数形结合思想、分类讨论思想、函数与方程思想、极限思想等.
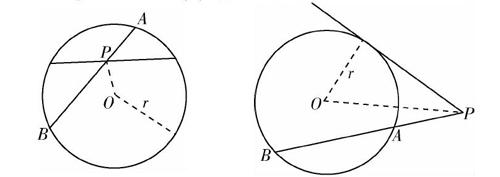
圆幂定理是相交弦定理、切割線定理、割线定理及推论的统称,其中相交弦定理与割线定理被欧几里得编入了《几何原本》(第三篇的第35个命题和第36个命题).这三个定理可以统一地表示为:过一定点P向圆O作任一直线交圆O于两点,定点P到两交点的距离之积为定值PA·PB=|OP2·r2|(|OP2·r2|),即如下图所示.
圆幂定理不仅在初中解平面几何题中有所涉及,在人教A版高中数学教材选修4-1第一章第三节对圆幂定理也有详细的介绍,是几何中的重要定理,因此,对圆幂定理的研究有很多.参考文献[1]-[3]从圆幂定理的应用角度探讨圆幂定理;参考文献[4]-[6]从圆幂定理的推广角度研究圆幂定理;参考文献[7]-[9]从教学设计角度研究圆幂定理.本文主要从数学思想方面探究圆幂定理,总结了圆幂定理在定理所蕴含的几何与代数转化的数学思想,几何中的运动变化思想,数学的统一思想三类数学思想,并由此提出了一些教学建议.
一、几何与代数转化的思想
圆幂定理描述了满足特定位置关系情况下的线段之间的数量关系,实质上就是把线段之间的长度关系用代数上的比例关系表达,因此,圆幂定理本身就可以看成是几何与代数的转换.在几何证明过程中,恰当地运用圆幂定理可以将几何问题转化为代数问题,从而简洁地解答几何问题.例如,运用圆幂定理求线段的长可以利用比例关系设出方程,解答方程得到未知线段的长.运用圆幂定理证明线段的长相等可以利用线段之间的比例关系的转化来证明.虽然学生在学习及应用圆幂定理过程中能够明确感受到将一个复杂的几何问题,有时把它转化为一个代数问题会更好地解决,但这仅仅是学生的一种数感,需要教师在教学过程中不仅渗透这种几何与代数转换的思想,还要对这种方法进行总结,以便学生在遇到几何问题时不仅仅局限于联想几何方面的知识,还能有将几何问题转化为代数问题的思维.
二、几何中的运动变化思想
在圆幂定理中,将弦内分(或外分)成两条线段的定点的位置是任意的,可以在圆内、圆上、圆外.因此,可以把它看成一个“动点”.当这个“动点”运动到圆内时,出现相交弦定理;当“动点”运动到圆外时出现割线定理,而这时将其中一条割线视为“动直线”变换到切线位置时就会出现切割线定理.在上述基础上,保持切线和“动点”的位置不变,将割线绕“动点”旋转使它经过圆心.设“动点”P(P在圆外)与圆心O的距离为d,圆的半径为r,切点为A.根据切割线定理可以得PA2=(d+r)(d-r)=d2-r2.这就把三个定理写成了圆幂定理的统一的形式.教师通过这种运动变化的思想来设计教学过程,不仅能使学生清楚明了地看到三个定理间的关系,而且还能加深学生对圆幂定理统一形式的理解.更重要的是让学生体会到几何中的许多问题都来自同一模型,虽然图形中的某些要素的位置关系不同,但本质是相同的,培养学生的辩证思维能力.
三、数学的统一性
(一)定理形式的统一性
相交弦定理、切割线定理、割线定理都能够统一成一种形式,即过一定点P向圆O作任一直线交圆O于两点,定点P到两交点的距离之积为定值(该点到圆心的距离与圆的半径的平方差的绝对值).
(二)证明结果的统一性
欧几里得在《几何原本》中运用了等面积法证明相交弦定理和割线定理,在高中数学选修4-1中运用了相似三角形来证明圆幂定理,还有人用极坐标来证明圆幂定理.虽然证明方法不同,但是,最后得到了相同的结论,反映了证明结果的统一性.
定理形式的统一方便学生对公式的记忆,证明结果的统一让学生感受到数学“殊途同归”的魔力.教师在教学过程中应带领学生一起鉴赏数学的统一美与简洁美,感受数学的魅力,增加学生对学习数学的兴趣.
在圆幂定理的教学设计中,教师渗透几何与代数转换的思想,运动变化思想,并引领学生鉴赏数学的统一美,笔者认为会取得好的效果.
【参考文献】
[1]王青.圆幂定理的应用[J].铜仁师专学报(综合版),2001(3):94-99.
[2]孟维帅.巧用圆幂定理解决直线和圆参数方程中一类问题[J].中学数学杂志,2018(5):46-47.
[3]刘亮.圆幂定理在解析几何中的巧用[J].中学生数学,2015(21):8-9.
[4]谢玉兰.圆幂定理在椭圆上的推广及其若干推论[J].中学数学研究,2018(8):26-27.
[5]陈波.从圆幂定理到圆锥曲线幂定理[J].数学教学,2016(5):42-45.
[6]谢兆帅.球幂定理——将平面中的圆幂定理推广到立体几何中[J].数学学习与研究,2015(7):102.
[7]李树臣.圆幂定理的教学设想[J].中学数学教学参考,1998(12):11-12.
[8]李琦玲.从圆幂定理谈教育数学和信息技术与数学课程的整合[J].语数外学习(高中版中旬),2015(2):33-35.
[9]刘敬烈.关于圆幂定理的教学设想[J].数学教学通讯,1985(1):4-5.
[10]许康.数学美与创造力[M].哈尔滨:哈尔滨工业大学出版社,2016.
[11]韩庆师.初等数学基础分析[M].天津:新蕾出版社,2009.
[12]孙月光.初中几何教学研究[M].上海:上海教育出版社,2000.
