浅海孤子内波对水平纵向相关性的影响∗
2019-11-30张泽众骆文于周益清
张泽众 骆文于 庞 哲 周益清
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
近年来,孤子内波、涡旋、海洋锋面等海水介质的不均匀性对声场的影响受到广泛的关注。我国具有广阔的海岸线,在我国南中国海大陆架海域常有孤子内波的观测报告出现,当孤子内波在声波传播路径上出现时,由于内波在水平方向上引起大范围的声速剖面起伏,从而引起声传播的起伏。有时这种起伏是相当可观的,可以在几十公里的距离上增加数十分贝的额外传播损失。
孤子内波作为影响声场的主要因素之一,一直是近年来水声研究的热点之一,人们对孤子内波展开了大量的工作。1991年,Zhou 等[1]指出孤子内波的存在会影响声场声压传播损失,这种影响与声源频率和孤子内波频率有关。1995年,美国新泽西大陆架海域浅海声传播实验SWARM’95 (Shallow Water Acoustics in a Random Medium)发现由于孤子内波的影响,导致声场能量有1∼7 dB 的起伏[2−5]。2001年–2003年,蔡树群等[6]分析了南中国海北部孤子内波现象,讨论了目前南中国海孤子内波研究中存在的一些问题。2011年,李整林等[7]分析了孤子内波引起的高号简正波到达时间起伏。
声场水平相干特性是影响声呐阵探测性能的重要因素。导致声场水平纵向相关下降的主要因素有介质的不均匀性和多途干涉,通过研究孤子内波对水平纵向相关性的影响,对分析孤子内波海域声呐探测具有重要的意义。由于海洋介质的不均匀性、海底不平、多途效应都会对声场的水平纵向相关性产生影响,因此对水平纵向性的研究得到了广泛的关注。宋俊等[8]从物理意义上研究分析了浅海孤子内波存在下水平纵向相关性的周期性变化。Guo 等[9]、Li 等[10]研究了水平纵向相关性半径与频率和距离的关系。胡治国等[11]研究了深海不平海底对水平纵向相关性的影响。
在研究声场的特性与规律时,通常采用波动理论、射线理论、简正波理论及抛物方程理论等声场分析方法。抛物方程方法采用步进算法计算声场,因此有利于计算环境参数随水平方向变化的声场。本文利用简正波理论对声线通过孤子内波后的声压进行了理论推导,并通过声压来计算出两点之间的水平纵向相关系数。然后通过二维抛物方程模型(Range-dependent acoustic model,RAM),仿真了浅海孤子内波对150 Hz 声场信号的水平纵向相关系数的影响。最后将仿真结果与理论推导结果进行对比,结果一致。
1 问题描述
1.1 波导模型
图1是浅海波导声速剖面示意图,海底为平坦海底并且深度为40 m,温跃层深度从15 m到27 m,温跃层以上海水声速为1530 m/s,温跃层以下海水声速为1480 m/s。上表面为理想海面,海底为液态半空间海底,海底声速为1530 m/s,密度为1.5 g/cm3,吸收系数为0.2 dB/λ。声速随深度分布表示式为

其中,c1和c2分别表示温跃层上下声速,z1和z2分别表示温跃层上下边界的深度,ξ(c1−c2)/(z1−z2)为温跃层声速负梯度。

图1 水平波导声速剖面图Fig.1 Horizontal waveguide sound velocity profile
1.2 内波模型
本文采用常见的双曲正割剖面,如果满足浅海条件,则单个孤子内波的KdV 方程的典型解析解为[2]

其中,η(r)代表孤子内波随距离的位移,∆代表波包宽度,a为孤子内波的幅度,r为水平距离,R为孤子内波中心位置。当传播路径上存在孤子内波时,声速表达式如下:当孤子内波距声源位置为8 km时,计算距离内的二维声速剖面如图2所示。


图2 孤子内波声速剖面Fig.2 Soliton internal wave sound velocity profile
2 水平纵向相关性
声场的水平纵向相关性刻画了在声传播方向上同一接收深度、不同水平距离处两个接收点的声场相似程度。设水听器分别位于声传播方向上相同深度并有一定纵向间隔的(r,Zr)和(r+∆r,Zr)两点,则这两个水听器同时接收到的信号波形之间的归一化互相关系数为水平纵向相关系数,定义为

其中,pr(t)和pr+∆r(t)分别表示两点接收到的声信号声压时域波形,τ为时延,∆r为水平纵向间隔,满足∆r ≪r。利用傅里叶变换可得频域内的水平纵向相关系数表达式:其中,Pr(ω)和Pr+∆r(ω)分别为两点接收到的声信号频谱,*表示复数共轭,ω表示角频率,ω0和∆ω分别表示发射信号的中心角频率和带宽,τ同样表示时延。
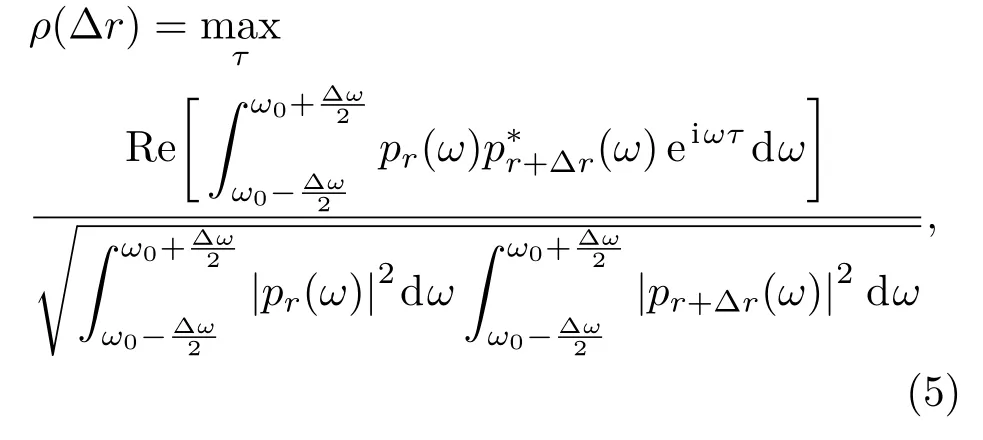
3 孤子内波对声场的影响
孤子内波环境的水平波导示意图如图3所示:孤子内波幅度为15 m,宽度为100 m,速度ν= 1 m/s;声源位于35 m;接收器位于深度为40 m、距声源10 km 处。计算接收器与接收器后距离∆r=100 m两点的相关系数。

图3 孤子内波水平波导示意图Fig.3 Horizontal waveguide diagram of soliton internal wave
用耦合简正波理论来描述图3所示的孤子内波存在时的水平波导问题。孤子内波将声场分为孤子内波前、中、后三部分,分别用符号I、II、III 来表示三个区域,声源的角频率为ω,然后计算单频声源的声压:

式(6)中,C#m和qm分别为第m号简正波本征值的模式系数和实部,ψm(z)为本征函数,并且服从归一化形式:

其中,ρω为海水的密度。
在区域I 和区域III,由于没有孤子内波的影响,所以简正波系数CIm、和本征值等不随距离变化而改变。假设声源深度为zs、功率为Ws时,可以得到区域I的简正波系数如下:

式(8)中,cs为声源处海水声速。区域II中由于孤子内波的存在,简正波系数(r)可以用一阶微分方程来求得:

其中,∆qmn=qm −qn,Vmn的表达式为
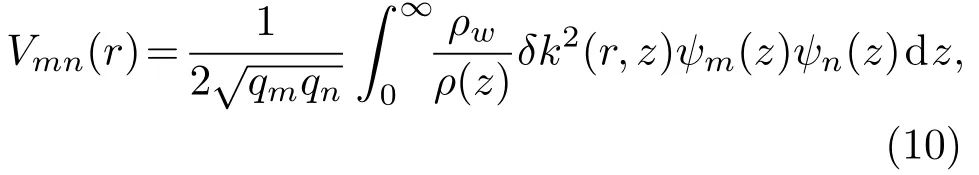
式(10)中,k(r,z)表示在区域II 中有内波扰动的波数,在区域I和区域III 中用k0(z)=ω/c0(z)表示无内波扰动时的波数,由于内波扰动引起的波数变化δk2(r,z),并且符合k2(r,z)=k20(z)+δk2(r,z)。

将式(11)代入式(9)可得
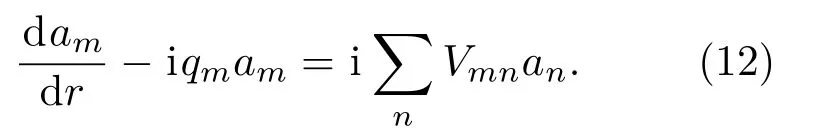
在区域II内,式(12)可以写成如下形式:

由式(13)可得矩阵U只与内波参数有关。然后分别利用区域I、区域II和区域II、区域III边界条件可得

式(13)中,Smn(L)=Umn(L)exp(−iqmL),并且同样只与内波参数有关与内波位置无关,则区域III中的声压可以写成:

式(15)中,

根据相关函数表达式可得

其中,Ωmnkl=Ωmn −Ωkl,当且仅当m=n或者k=l时所对应分量对声强起伏起主要作用。
运用抛物方程模型(RAM)对上面的波导环境进行仿真,中心频率是150 Hz,带宽50 Hz,可以得出前五号简正波的数值,如表1所示。

表1 简正波模型计算得到的前五号简正波数值Table1 The first five normal wave values calculated by normal wave model
通过公式(17),已推导出浅海孤子内波环境下两点水平纵向相关系数的一般表达式,它是由多号简正波共同干涉作用的结果。当在上述波导环境中时,因为只有两号简正波起主要作用,这样就会得到与文献[8]相同的表达式,但是当环境中存在多号简正波起主要作用时,文献[8]的表达式就不再适用,只能运用本文推导出的公式(17)来进行研究。并且它反映出水平纵向相关系数只与孤子内波的速度和特征宽度有关,而孤子内波幅度变化不是很大时对水平纵向相关系数周期和幅度的影响甚微,可以忽略。
根据上述波导环境将前两号简正波数值代入前面理论得到的结果,由公式(17)可得周期性只与exp(−(qm −qn)vt)有关,只有两号简正波的周期性可以表示为

其中,v表示孤子内波速度。如上所设v=1 m/s,得t ≈2π/(v|q1−q2|)=6 min。
在理论推导得出水平纵向相关性随时间变化的基础上,再利用上述环境和抛物方程模型得到的声压数据来计算水平纵向相关系数,如图4所示:蓝色实线表示模型计算得到的水平纵向相关系数,红色虚线表示理论计算结果,理论值与计算值得到水平纵向相关系数周期约为6 min,并且水平纵向相关系数幅度大小也基本吻合。
从物理机制上对只有两号简正波时水平纵向相关系数的周期性进行阐述。图5传播损失中也可以看出前两号简正波干涉距离r= 2π/|q1−q2| ≈0.36 km,当孤子内波未经过前两号简正波干涉区域时,都会对水平纵向相关系数产生一次影响,文中设孤子内波速度v= 1 m/s,得到干涉周期t=r/v= 6 min,与前面得到的结果一致。这样就从理论公式、模型仿真和物理意义上共同导出只有前两号简正波环境下水平纵向相关性的周期。

图4 孤子内波幅度为15 m 水平纵向相关系数Fig.4 Horizontal longitudinal correlation coefficient variation curve with time

图5 接收深度40 m 传播损失曲线Fig.5 Propagation loss curve at 40 m reception depth
下面来看孤子内波幅度的改变对水平纵向相关性的影响。从公式(17)中可以看出,水平纵向相关性与孤子内波幅度无关而与孤子内波的特征宽度有关,当只有孤子内波幅度变化时对水平纵向相关系数不会有影响,但是当幅度的改变造成特征宽度改变时,就会对水平纵向相关系数造成影响。由图6可以看出,当孤子内波幅度减小到10 m 时,水平纵向相关系数和孤子内波幅度为15 m 时基本一致,并不影响水平纵向相关系数的大小和周期性。所以当孤子内波幅度变化很小时对水平纵向相关系数幅度和周期的影响可以忽略,这与模拟得到的结果一致。

图6 孤子内波幅度分别为15 m、10 m 时水平纵向相关系数Fig.6 The horizontal longitudinal correlation coefficient when the amplitude of the soliton internal wave is 15 m and 10 m
4 结论
本文通过简正波理论和孤子内波边界条件推导出孤子内波后方的声压表达式,然后利用声压推导出两点的水平纵向相关系数一般表达式,适用于所有浅海孤子内波环境。然后对中心频率为150 Hz的声信号用抛物方程理论进行仿真计算,并与理论推导对比验证推导出的水平纵向相关系数。得到以下结论:
(1)孤子内波存在情况下,简正波干涉显著影响声场水平纵向相关性。
(2)在本文特定浅海环境的水平波导情况下,由于前两号简正波占主导地位,所以水平纵向相关性会随时间呈现出周期性变化,在文中所设环境和信号及内波参数情形下,周期为6 min。但是当波导环境变化,多号简正波占主导地位时,要利用公式(17)重新进行推导,公式t= 2π/(v|q1−q2|)将不再适用。
(3)孤子内波幅度变化不是很大时,其幅度改变不会引起水平纵向相关系数周期和幅度的显著变化。
5 研究展望
孤子内波作为声折射率显著不同于无内波区域的一种特殊不均匀水团,关于其对声场的研究更加深入,本文忽略了孤子内波的水平折射效应,研究了对二维声场水平纵向相关性的影响,未来将在以下方面完善对孤子内波研究的工作:
(1)由于孤子内波的水平折射效应不可忽视,已经建立适用于孤子内波环境的三维耦合简正波模型,下一步将利用三维模型研究孤子内波对三维声场的影响以及对三维声场水平纵向相关性和水平横向相关性的研究,并通过实验验证仿真结果。
(2)孤子内波与声源和接收器的相对位置对三维声场的影响很大,将考虑三维声场中孤子内波位置的改变对水平纵向相关性的影响。
