利用声音反射信号重建室内空间结构的研究∗
2019-11-30宋浠瑜罗丽燕覃虹菱
李 悟 王 玫 宋浠瑜 罗丽燕 覃虹菱
(1 桂林电子科技大学 认知无线电与信息处理省部共建教育部重点实验室 桂林 541004)
(2 桂林理工大学信息科学与工程学院 桂林 541004)
0 引言
在室内声源定位的过程中,由于复杂的室内环境造成的混响会干扰对声源位置的判断,很难仅仅通过传声器阵列对声源进行准确定位。近年来对声源定位的一系列研究表明,在已知室内空间结构的前提下,可以建立更加准确的室内混响模型,有效分离反射信号和直达信号,实现更加精准的声源定位。如文献[1–2]提出:在进行声源定位之前,利用定向声源估计地板、天花板和墙的位置对于辅助声源定位具有重要的作用;文献[3]同时提出:利用有限元分析法建立的室内声场模型可以辅助多声源同时定位。
在研究室内空间结构重构方面,声信号易于收发处理被视为实现室内结构重构的理想信号。关于这方面的研究,不少学者也做出了很多杰出的工作。Dokmanić 等[4]在2011年提出了基于声源传声器一体的方案,借助image 模型利用一阶、二阶反射信号到达时间,通过矩阵变换确定房间结构;文献[5]提出利用脉冲信号的反射到达时间和遗传算法估计矩形或者L 形房间的几何结构;文献[6]提出将传声器和声源假设为椭圆的两个焦点,通过寻找公切线的方式确定墙壁位置;文献[7]利用墙面反射系数、各墙之间的距离、方位角、房间高度建立房间冲激响应模型,通过L1 正则化成本函数来求解以上数值重建出房间结构;Dokmanić 等在文献[8]中改善了他们的方案,利用欧式距离阵(Euclidean distance matrices,EDM)特性分类一阶反射信号到达时间,借助image模型重构出房间结构。
以上方法虽然在一定程度上解决了房间几何重构的问题,但是每一种方法都有其局限性。文献[4]提出的方法利用了二阶反射信号,但是,由于二阶信号十分微弱,不能保证每次实验都能接收到完整的二阶信号,缺乏实用性;文献[5]提出的方法需要找到一个合适的物理模型才能说明其理论的正确性;文献[6]提出的方法利用了一阶、二阶反射信号的第一到达时间,但是该时间无法通过冲激响应直接判断;文献[7]提出的方法需要处理一个非常复杂的矩阵,对建图效率有很大影响;文献[8]提出的方法引入了欧氏距离阵,但是这种方法在收发存在时间延迟的情况下误差很大,时间延迟来源于信号收发处理时间、信号响应时间和介质中传输的时间,尤其是介质中传输的时间在室内这种复杂的多径环境下很难精确测定,无法直接去除。本文针对文献[8]方法中引入的信号传播距离存在误差的问题,提出了一种基于到达时间差(Time difference of arrival,TDOA)最小二乘误差的室内建图方案,利用到达时间做差的方法消除时间延迟,通过最小二乘误差判断一阶反射信号,并实现待测房间几何结构的推测。
1 系统设计原理
1.1 image模型
image 模型是由Allen 等[9]提出的一种描述小房间混响的声学模型。文中假设声源发出的信号一部分沿直线传播直接被传声器所接收,另一部分经过墙面或者障碍物反射被传声器接收,反射符合镜面反射规律,入射角等于反射角。该方法利用反射阶数(声波经过墙壁、地板、天花板反射的次数)和房间维数表示房间混响,适用于具有规则几何结构的房间。声音在房间内传播模型类似于一个多径信道,描述房间信道情况可以用以下公式表示:
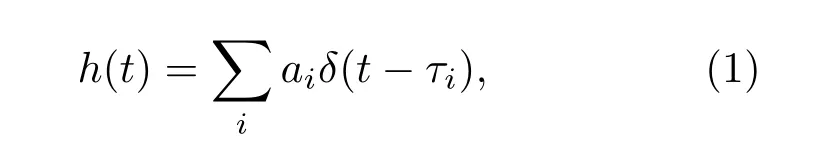
式(1)中,h(t)代表房间时域冲激响应,ai代表每一个信道的增益,τi代表每一个信道的时延。image模型如图1所示。
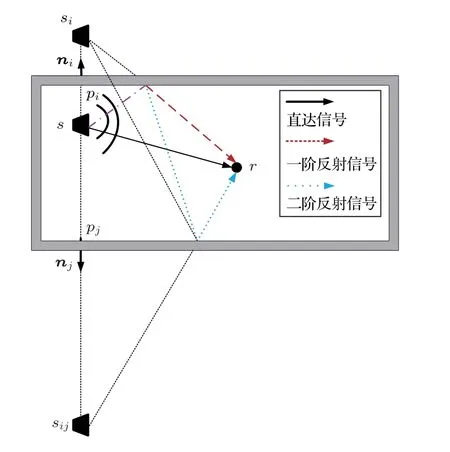
图1 image 模型下的一阶镜像源和二阶镜像源Fig.1 Image source model for first-and secondorder echoes
根据image模型:一阶镜像声源(经过一次墙面反射的镜像声源)坐标和声源坐标关于每一面反射面(墙、天花板、地板)轴对称,而镜像源和传声器的连线与反射面的交点为反射点。声源坐标定义为s,镜像声源坐标定义为si,声源一阶镜像声源点连线与墙线交点坐标定义为pi,ni定义为与实声源一阶镜像声源连线共线的指向镜像声源的单位向量,pi −s指声源指向pi点的向量,指两个向量的内积也就是声源点s到pi的距离,一阶镜像声源si可以表示为[8]
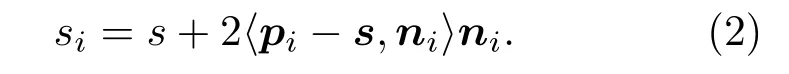
一阶镜像声源点二阶镜像声源点连线与墙线交点坐标定义为pj,nj定义为与一阶镜像声源二阶镜像声源连线共线的指向二阶镜像声源的单位向量,pj −si指一阶镜像声源指向pj的向量,⟨pj −si,nj⟩指两个向量的内积也就是一阶镜像声源点si到pj的距离,二阶镜像声源和一阶镜像声源关于另一面墙轴对称用sij表示,sij可以表示为[8]
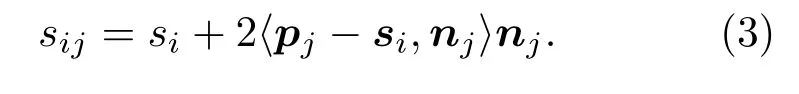
实际上,实声源和一阶镜像声源连线的中垂面就代表了房间的墙面、天花板、地板所在的位置,得到了实声源的坐标和所有一阶镜像声源的坐标相当于得到了房间的几何构型,求解实声源和一阶镜像声源的位置就是实现室内构图的途径。
1.2 室内建图存在的问题
由以上内容可知,为了求解实声源和一阶镜像声源坐标,根据声信号到达时间公式:

式(4)中,c代表声信号在空气中的传播速度,r代表传声器的位置,∥si −r∥代表声源到传声器的欧式距离。ti可以利用室内冲激响应来得到,传声器阵列r的位置已知。要求解声源si还需要解决以下几个关键问题。
1.2.1 反射信号到达传声器次序不一致
TOA(Time of arrival)代表到达时间值。对于直达信号来说,信号到达的先后顺序代表声源到传声器位置的远近,由此可以很容易判断每一个信号来自哪一个传声器。但是对于一阶反射信号来说,先收到的反射信号不一定来自同一反射面,反射信号受到声源传声器反射面三者位置关系的共同影响,有时会出现反射次序颠倒的问题,如图2[8]所示同一个声源发出的信号传声器1先收到蓝色面反射的,而传声器2 先收到红色面反射的。因此不能认为反射信号都是以同一次序到达的。无法判断反射信号的来源,定位声源坐标也就无从谈起。

图2 反射信号到达次序不一致Fig.2 Echo swapping
1.2.2 高阶反射信号干扰
由于二阶及其以上反射信号非常微弱,不能保证每次实验接收到完整的二阶信号,对于建图来说,高阶信号是不需要的成分,需要将其视为干扰进行去除。如图3所示,横轴代表到达时间,纵轴代表时间域房间冲激响应(Room impulse response,RIR)。

图3 高阶反射信号干扰Fig.3 Inference by higher-order echoes
1.3 解决方案
针对1.2.1 节提出的反射信号到达次序不一致的问题,最早研究利用声信号进行房间重构的Dokmanić 等在经典文献[8]中提出了利用欧式距离阵特性为反射信号归类的方法。
欧式距离阵指的是假设欧几里得空间X中存在N个点,

X中任意两点之间的欧式距离的平方可以表示为

展开式(6)得到

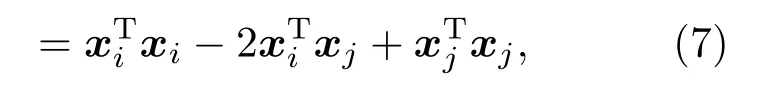
所有欧式距离平方可以构成欧式距离阵D= [dij],定义为

其中,diag 代表对角阵,1 代表所有元素都为1 的向量,EDM包含完整的节点信息,而且形式易于处理,利用EDM可以重建这N个点的位置。
首先,将传声器之间的欧式距离作为矩阵的一部分元素建立欧氏距离阵,另一部分元素来源于根据冲激响应测得的反射信号到达时间转换成的传播距离,这部分距离作为扩展与原矩阵组成增广矩阵,如图4所示。

图4 基于欧式距离阵的反射信号归类法Fig.4 Process of echo sorting by EDM
多维尺度分析法(Multidimensional scaling,MDS)是一种对EDM 经过变换来反推出符合约束条件的声源位置以及传声器位置的方法。假设X为待求的声源位置与传声器位置的坐标,x1坐标为原点,MDS可以表示为
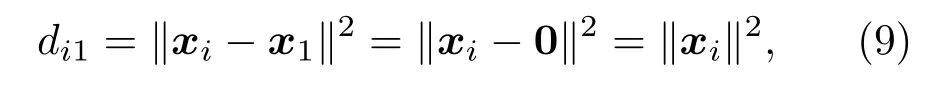
于是,

其中,d1=De1,解算XTX可得

由于XTX为方阵,利用特征值分解可以得到

其中,Λ= diag(λ1,··· ,λn),Λ为以XTX特征值为元素的对角阵,U是正交化特征向量。求解X,可以得到

为了优化重构结果,这里引入了s-stress 的概念。s-stress 用来计算重构出的点组成的EDM 与原EDM 之间的差距,可以衡量重构的准确性,计算公式如下:
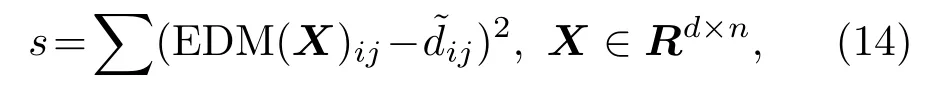
具体算法过程如下:
(1)分别计算各传声器得到的房间冲激响应。
(2)从各冲激响应里随机选取到达时间,通过公式(4)转换为传播距离。
(3)计算各传播距离的平方与原EDM 组成的增广矩阵。
(4)利用MDS 算法重构出组成矩阵的各点的坐标。
(5)计算出重建点的EDM与原EDM之间的差距s。
(6)重复以上步骤(2)∼步骤(5),直至遍历所有到达时间值。比较s的大小,其中令s最小的一组的到达时间可以被归为一类。
(7)当归类好一组到达时间,去除该组到达时间值继续分类直到结束为止。
利用欧氏距离阵分类反射信号是一种经典算法。最重要的是,这种方法借用了s-stress 的思想,重建结果是否符合预期的标准在于EDM 中的每一个距离元素是否是准确有效的,只有真实的一组来自于同一镜像声源的信号才是符合传播规律的使s值最小,因此才能成功为反射信号分类。但是,随着后期关于欧式距离法研究的深入,这种方法的不足之处也逐渐显现了出来。最重要的一点在于上文提到的分类的成功与否完全取决于距离元素的准确性。基于TOA 分类算法最大的弊端在于发射端和接收端之间存在的延迟很难处理,这些延迟包括信号处理收发的时间、信号响应时间和介质中传输的时间,介质传输的时间受温度以及室内环境影响很大。因此,这些延迟不是精确已知的,是随着时间而变化的变量。相当于实际得到的到达时间为

其中,R代表实际距离,c代表声速,∆代表收发存在的延迟,β代表测量误差。为了在室内达到10 cm的精度,假设在20◦C 的常温条件下声速为343 m/s,那么延迟不能大于0.3 ms。而在实际测试中,由于温度、线路、编码解码速度的影响,信号会出现2∼3 ms 的浮动误差,利用带有较大误差的距离进行重建显然会严重影响对反射信号归类的判断,而且还会影响求解出的声源位置的精度。
1.3.1 基于到达时间差的声源定位法
现有的利用到达时间差进行定位的方法叫做到达时间差(TDOA)法,又称为双曲线定位法,TDOA 法的最大优点在于能够通过TOA 之间做差消除常量时延项∆。在三维空间中需要至少四个传声器才能进行定位。待测声源发出的信号达到其中两个传声器之间的时间差形成以这两个传声器为焦点的双曲面,四个传声器可以形成三对双曲面,其中每两个单边双曲面相交于一条线,这两条线的交点就是声源的位置。
为了得到更加准确的定位结果,一般使用基于最小二乘误差的迭代方法来求解目标声源坐标,这种方法首先定义成本函数,表示声源目标定位精度,成本函数定义为[10]

其中,wi是权重,c是声速,是第i个传声器到达时间和基准传声器到达时间差的估计,di是待测目标与第i个传声器之间的距离值。假设目标声源的位置估计为

令成本函数公式(16)最小,可以得到声源坐标为

牛顿法、梯度下降法、高斯牛顿法、莱温伯格-马夸特法都可以用来结合公式(18)求解声源坐标,这里不再赘述具体算法。
1.3.2 基于最小二乘误差的匹配算法
为反射信号分类的思想实际还是声源定位的过程,一组反射信号能够分为一类是因为它们存在一个共同的镜像声源点。那么只要选取一组到达时间,将它们转换为传播距离,检验符合传播的条件下是否存在一个共同的交点即可。注意到两个传播距离做差可以表示为一组双曲线,那么取其中一个传播距离分别与其他n个传播距离做差就可以形成n条双曲线。如果n条双曲线可以确定唯一的一个交点,这个点就是可能的一个声源坐标,这组距离匹配成功。否则,如果不存在交点,这组距离匹配失败,原理如图5所示。

图5 利用双曲线法进行匹配的过程Fig.5 Matching echoes by TDOA method
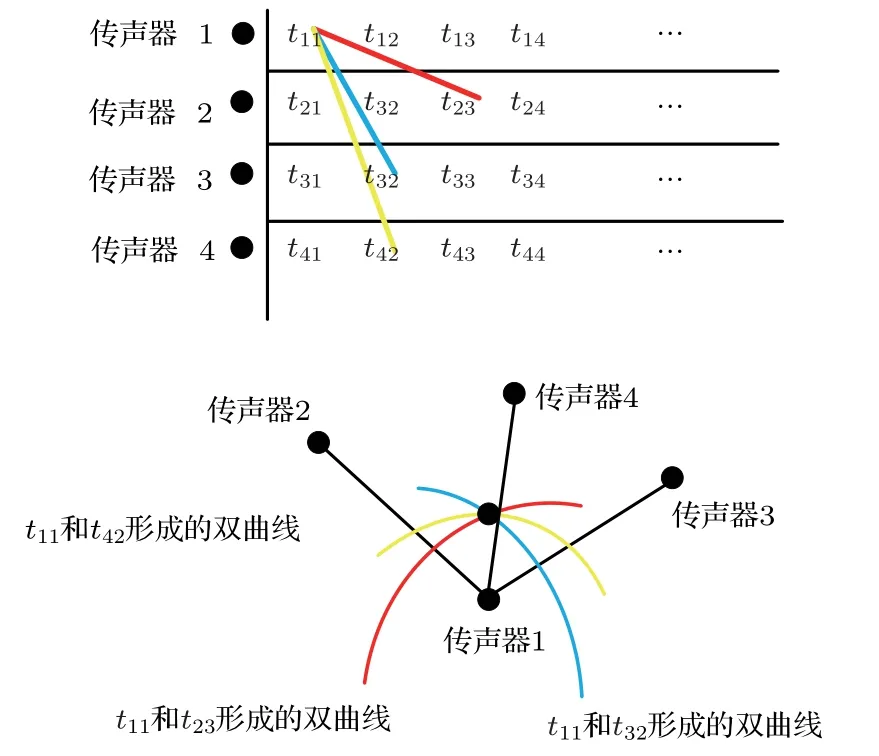
图6 反射信号遍历的过程Fig.6 Matching TOAs by the least square method combing TDOA method
算法过程如下:
(1)假设存在k个传声器,分别计算各传声器得到的房间冲激响应。
(2)从各冲激响应里得到信号到达时间t,第1个小标代表传声器序号,第2 个小标代表接收到信号的次序,例如t23代表第2 个传声器收到的第3 个反射信号。
(3)首先,令i= 1,l= 1,m= 1,···,r= 1,ε= +∞,p= (0,0,0),i < n。e为待求最小二乘误差,o为待求镜像声源坐标。
(4)以传声器1 为基准传声器,取t1i与t2l,t3m,···,tkr组成一组1× k维数组进行最小二乘误差匹配求解e(x,y,z)和坐标o。
(5)如果满足e < ε,则令ε=e,p=o。如果不满足转入第(6)步。
(6)令r=r+1,检验t1i −τ < tkr < t1i+τ是否成立。如果成立,转入第(4)步;如果不成立,令k −1=k,r=1。
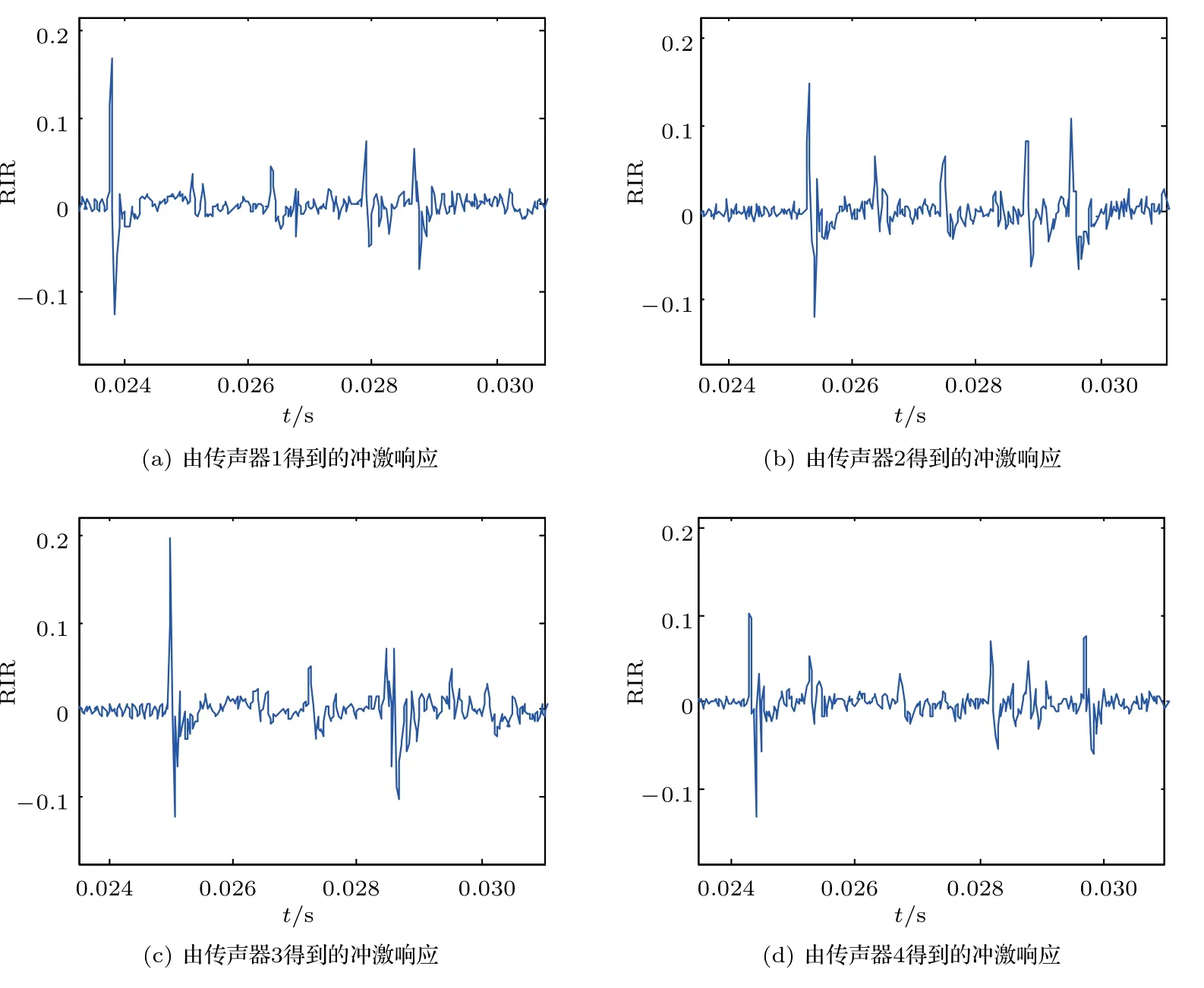
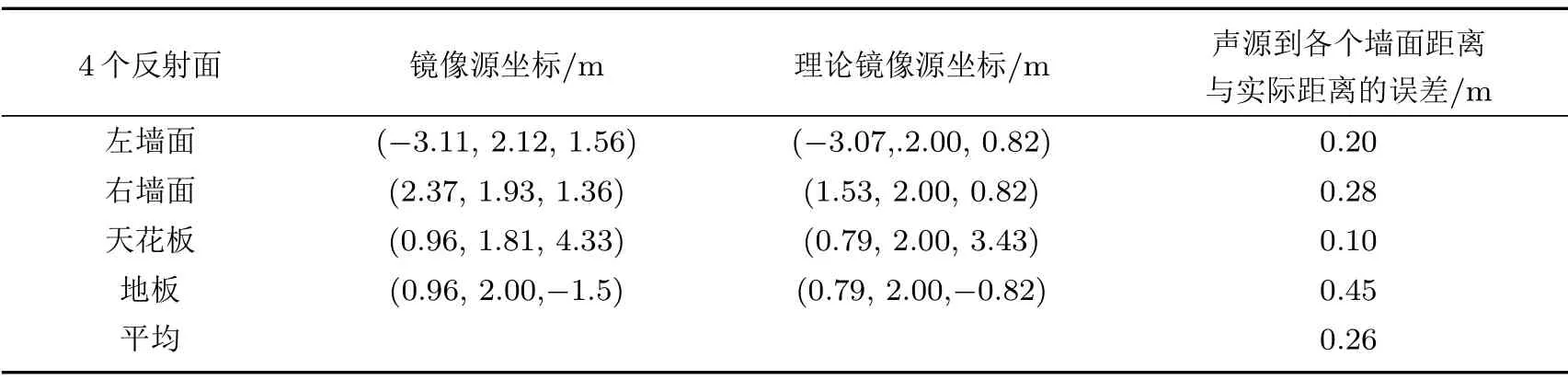
(7)检验t1i −τ ······ (8)检验t1i −τ < tlr < t1i+τ是否成立。如果成立,转入第(4)步;如果不成立,输出坐标p,此时使ε最小的一组到达时间t1i,t2l,···,tkr被分类成功。 (9)令i=i+1,l= 1,m= 1,···,r= 1,ε=+∞,p=(0,0,0)。 (10)检验i > n是否成立。如果成立,结束程序;如果不成立,转入第(4)步。 针对第(6)步不等式需要说明的是,考虑到优化算法的复杂度,不需要对每一个TOA 值都进行匹配,根据三角形原理,两边之差小于第三边,经过同一墙面反射到达传声器阵列的信号之间的波程差小于阵列两个阵元之间距离的最大值,因此在匹配的过程中设置t1i −τ ∼t1i+τ,τ=dmax/c的搜索门限就可以大大提高匹配效率。上述算法流程可以用图7表示。 1.3.3 关于信号TOA的修正 通常情况下,在确定信号到达时间时,普遍采用选择信号冲激响应的最高峰当作信号到达时间。实际上,由于传声器阵列无法做到完全的同步,再加上人为测量误差的影响,选择最高峰作为信号到达时间是不准确的,在远场定位情况下这种误差会被放大,从而影响对实际声源和镜像声源的判断。假设在44.1 kHz的采样频率下,一个冲激响应由10个采样点组成,如果信号到达时间分别位于第1 个采样点和第10个采样点,此时依然采用最高峰到达时间的话就会引入7 cm 的误差。由于直达信号易于分离,本文采用利用直达信号对反射TOA进行修正。 图7 算法流程图Fig.7 Algorithm flow chart 图8 利用直达信号修正反射波TOAFig.8 Illustration of amending reflective TOAs by matching direct signals 如图8所示,取完整直达信号峰值内的几个采样点(如图8红线内)分别进行最小二乘匹配,找到实际代表信号到达时间的位置,计算出最佳采样点位置与峰值的差距τ,在后面进行反射信号匹配时分别以tnm±τ来代替反射信号到达时间tnm,可以起到修正不同步的作用,实验证明利用这种方法进行修正可以消除4∼5 cm误差。 上述方法实现了信号的归类以及镜像声源的求解,解决了1.2.1 节的问题。对于1.2.2 节高阶干扰的问题,考虑将其转换为高阶镜像声源来去除。按照匹配的步骤从先到达的TOA 匹配到后到达的TOA,先求出镜像声源坐标可以认为是低阶镜像声源,后求出的为高阶镜像声源。考虑到二阶及其以上的声源满足图1几何关系,在这里规定,如果新求出的声源与已有的声源满足如下规律, 那么就认为新求出的声源坐标是一个二阶及其以上阶的声源。其中,s1、s2分别代表已有的声源和新求出的声源,公式(19)来源于公式(3),公式(20)中的p2代表新旧声源连线的中点,公式(21)中的n2代表已有声源指向新声源的单位向量。去除高阶干扰后再结合待测房间结构去除不合理的镜像声源就可以得到真正的一阶墙面镜像声源,从而通过几何关系得到房间的几何构型以及尺寸。 实验场景选择在桂林电子科技大学第七教学楼实验室走廊进行,走廊是宽为2.3 m、高度为2.37 m 的狭长结构,前后没有墙壁遮挡,大小合适,中间也没有其他障碍物阻挡传播路径,是理想的实验场景。实验目的是还原出左右两面墙和天花板以及地板的位置,也就是实验场景的正面轮廓。传声器选用Behringer ECM 8000 全向型传声器4 个,声源选用哈曼卡顿aura studio 音响,外置声卡选用M-AUDIO M-TRACK QUAD 4 通道声卡,另外利用一台惠普笔记本发射、采集和处理数据。为了便于去除直达信号和防止共振带来的干扰,将声源设置在距离传声器阵列较远的地方,声源距传声器阵列中心2 m,同时为了区分出左右墙的区别,声源设置在距离右边墙壁0.36 m、左边墙0.94 m 的地方,高度为0.82 m。传声器阵列采用4 个传声器设置成常见的十字形阵列,这种结构能够保证不管声源在任何位置都能处于阵列的开口方向。传声器之间的间距为0.6 m,M1∼M4 高度均为1.31 m。传声器阵列和声源与外置声卡相连,利用笔记本电脑上的abode audition 2018 采集传声器阵列接收到的信号,利用MATLAB进行后期处理。实验场景俯视图和正面实景图如图9所示。 图9 实验场景俯视图和正面实景图Fig.9 Arrangement of experimental equipment and picture of the corridor 本文选择函数形式如下的正弦扫频信号作为激励信号[11]: 根据文献[11],这种信号比较适合于求解系统冲激响应信号。根据频率响应,设定w1为500 Hz,w2为5000 Hz,T为信号时长,设置为0.01 s。 设置采样率为44.1 kHz,利用频域接收信号Y(ω)和频域发射信号S(ω)经过公式(23)计算得到的四个通道冲激响应,经过傅里叶逆变换得到的时域冲激响应如图10所示。 从图10 可以看出,率先到达的峰对应直达信号,随后反射信号依次到达。以传声器正中心靠近地面的位置为坐标原点,以走廊通行方向为y轴,以垂直两墙壁方向为x轴,以地板到天花板的垂直方向为z轴,利用四个直达信号的TOA得到声源坐标为(0.76 m,2.01 m,0.70 m)。在直达波到达后50 ms内进行搜寻,分别利用设置阈值的方式挑选出直达波后的10 个到达信号,选择这10 个的到达时间组成10×4 的一组数据,经过匹配算法分别求得声源坐标为(1.46 m,2.02 m,0.72 m)、(−3.05 m,1.96 m,0.82 m)、(0.83 m,1.97 m,3.45 m)、(0.77 m,2.03 m,−0.94 m)、(0.40 m,1.95 m,1.13 m)、(0.94 m,1.39 m,−1.46 m)、(1.09 m,−0.42 m,−2.03 m)(由于后3 个峰值到达时间不满足间隔小于阵列最大间距所对应的时间值,因此没有产生声源坐标)。绘制以上坐标在x、z方向的投影如图11所示。 图11 中五角星代表实际声源,×坐标经过公式(19)∼(21)检验不符合二阶声源定义,(0.40 m,1.95 m,1.13 m)离实声源太近显然不是符合镜像声源常理,(0.94 m,1.39 m,−1.46 m)、(1.09 m,−0.42 m,−2.03 m)这两个坐标y轴偏差太大,也可以排除。因此它们代表由噪声产生的错误声源,圆圈代表一阶镜像声源。利用真实声源和镜像声源,作它们连线的垂直平分线可以得到图12。 图10 四个通道测得的房间冲激响应Fig.10 RIRs measured by a 4-element microphone array 图11 利用TDOA 最小二乘误差法得到的镜像源坐标Fig.11 Illustration of mirror source coordinate 图12 利用TDOA 最小二乘误差法得到的走廊结构与实际走廊结构的对比Fig.12 Comparison of measured corridor structure by the least squares of TDOA and real corridor structure 图12 对应代表利用最小二乘法求出的走廊左右墙面、天花板、地面的位置以及与真实值的对比。从表1可以读出声源到各个墙面距离的误差分别为0.01 m、0.02 m、0.05 m、0.12 m,x轴方向平均误差为0.03 m,z轴方向平均误差为0.17 m,整体平均误差为0.05 m。在一定误差范围内实现了对走廊的几何重构。 作为对比,利用欧式距离法得到走廊结构以及与实际情况的对比如图13、表2所示。 表2可以得到声源到各个墙面距离的误差分别为0.20 m、0.28 m、0.10 m、0.45 m,x轴方向平均误差为0.48 m,z轴方向平均误差为0.55 m,整体平均误差为0.26 m。可以明显看出,本文提出的方法是优于欧式距离法的。 图13 利用欧氏距离法得到的走廊结构与实际走廊结构的对比Fig.13 Comparison of measured corridor structure by EDM and real corridor structure 综上所述,本文的贡献在于:(1)由于现有的建图算法基本都借助于室内冲激响应或者信号相关来得到信号传播距离,但是由信号收发编码解码的时间、线路耗材传输的时间等造成的时延会引入较大误差造成图像的严重失真,本文提出的方案通过信号TOA 做差消除系统时延带来的影响,利用最小二乘误差为信号归类,实现了较好的建图效果。(2)本方法在算法上可以实现合二为一,在进行匹配的过程中同时可以完成镜像源坐标的定位,针对欧氏距离法先匹配归类再计算坐标的方法在复杂度方面进行了优化。 表1 测试结果与实际情况的对比Table1 Comparison of measured data by the least squares of TDOA and real data 表2 测试结果与实际情况的对比Table2 comparison of measured data by EDM and real data 本文提出了一种依托image 模型,利用到达时间差最小二乘法为一阶反射波进行分类,之后利用室内声场模型实现室内空间结构重构的算法。相比于其他室内空间建图的方法,这种方法原理简单,利于实现,而且不需要额外的专业器材,只需要利用常见的传声器组成的传声器阵列和普通全向音响就可以实现较好的效果。在此基础上,为了进一步提高室内建图的精度,今后可以考虑以下方案做出改进:(1)采用全向性更好的12 面体声源;(2)增加传声器阵元的数量以及利用更有效的三维阵型;(3)利用TDOA和其他定位算法的结合实现更加精准的远场定位。本文实现了具有规则几何图形的重建,考虑到后期复杂场景的重建,可以考虑引入移动机器人测量的方法,将非直线墙(例如,折线或曲线)分为一个个小的直线,每隔一段时间发射信号并接收来探测绘制墙线。这将是未来实现复杂室内构图的一个发展方向。

1.4 建立室内图形

2 实验结果
2.1 实验场景

2.2 实验步骤
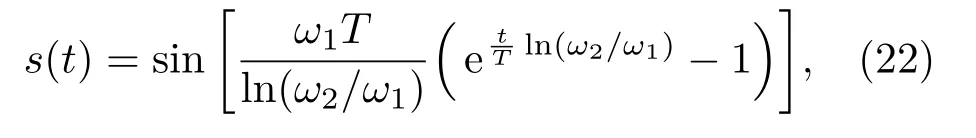

2.3 实验结果与对比




3 结论
