吸声型薄膜声学超材料低频宽带吸声性能研究∗

张忠刚 朱浩宇 罗 剑 马炳和

(西北工业大学 空天微纳系统教育部重点实验室 西安 710072)

0 引言

低频噪声控制是噪声控制中极具挑战的一个方向。低频声波传播距离远，普通的线性材料例如泡沫复合板，其耗散功率与声波频率二次方成正比，低频吸声效率很低[1]。薄膜吸声超材料(Membranetype acoustic metamaterials,MAM)通过在张紧的薄膜上固定刚性金属片，通过增加共振模式提高了低频声波在薄膜吸声超材料内部的能量密度；金属片拍动时与弹性膜接触边界包含增强的弹性曲率能量，与声波辐射模式耦合作用微弱，形成了类似共振腔的声波强吸收[2−5]。薄膜吸声超材料虽然实现了亚波长共振结构的低频有效吸声，但存在吸声频段窄、吸声系数低等问题。

2012年，Mei 等[5]制备出吸声型薄膜声学超材料，将厚度为0.2 mm 的半圆形金属片对称固定在张紧的硅胶薄膜上，实验结果显示，吸声型薄膜声学超材料样件在100～1000 Hz 内产生了多个共振吸收峰，实现了“单片薄膜超材料实现宽频吸声”的效果。随后，Yang等[6]制备了基于单极共振和偶极共振形式的双层超材料结构，实验结果显示，在特定频率附近，吸声系数达到99.7%。2014年，Chen等[7]通过理论分析证实单层薄膜吸声超材料的吸声系数不会超过0.5，但吸声单元上布置的金属片数量会影响吸收峰的数目。2015年，Yang等[8]得到了与Chen 相同的结论，Yang 等将不同质量的金属片固定在8 个单元的薄膜上，实现了200 Hz～1 kHz范围内的多个共振吸收峰，但仅有4 个吸收峰的吸声系数超过0.2。

2017年，程宝柱[9]将上述不同质量金属片对称固定薄膜上的结构定义为质量非对称结构，相同金属片非对称固定在薄膜上的结构定义为位置非对称结构，并对两种结构薄膜吸声超材料的吸声机理进行了研究。研究发现，位置非对称型薄膜声学超材料虽然理论上能在薄膜上累积较多弹性应变能，但实际仿真结果并不理想；通过对每一个质量片赋予不同的密度组成的质量非对称结构在高频区域的吸声系数有明显提升，按照升序或降序排列的结构吸声系数较为稳定。但密度梯度因为材料选择的问题难以实现。

本文采用了另一种质量非对称结构的表现形式，即通过赋予质量片不同的厚度实现质量非对称结构。相比于原先改变密度的方法，使用改变厚度的方法制作的薄膜声学超材料拥有更加优良的吸声性能，且易于实现。

综上所述，本文旨在优化拥有质量非对称结构的吸声型薄膜声学超材料的结构形式，将其制作为易于加工制造的声学超材料样品，并使用声学阻抗管测试系统对样品的吸声性能进行测试，进而利用仿真结果分析样品的吸声性能，提升该类声学超材料的实用性。

1 理论模型及仿真

图1展示了本文设计的声学超材料仿真模型，该模型由四个单胞组成，每块单胞中固定的薄膜相互独立。薄膜上嵌有厚度不同的半圆形质量片，半径为6 mm，其厚度按照等差数列的形式有序排布[8]。不同厚度质量片分布情况由图2示出。

图1 结构建模示意图(单位: mm)Fig.1 Schematic diagram of structural modeling

图2 质量片厚度分布示意图Fig.2 Thickness distribution of different mass sheets

1.1 吸声机理

吸声型薄膜声学超材料之所以能够有效吸声，是由于薄膜系统与声场发生共振耦合时，质量片与薄膜发生活塞式的整体运动导致。如图3所示，当发生此类运动时，质量片与薄膜的连接处会与没有贴合质量片的薄膜部分之间产生位移不连续区域。

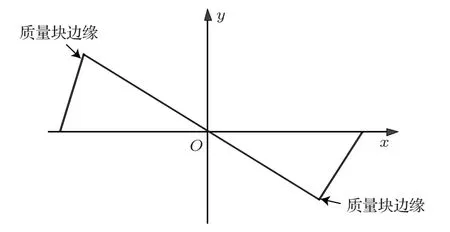
图3 薄膜形变二维示意图Fig.3 Two-dimensional schematic diagram of thin film deformation

薄膜的弹性应变能密度表达式为[1]

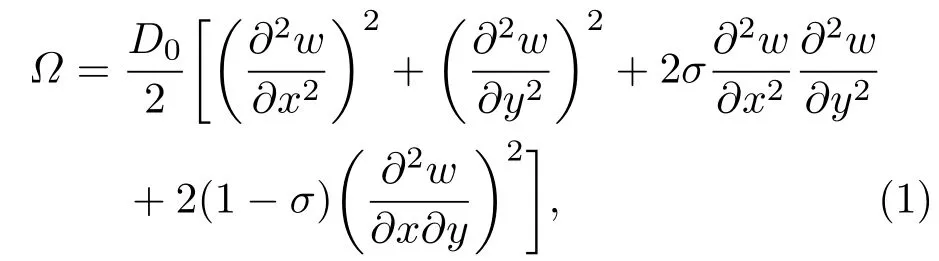
式(1)中，D0=Eh3/12(1−σ2)，E表示材料的杨氏模量，σ表示材料的泊松比；w表示薄膜沿垂直方向的位移；h表示薄膜的厚度。

由式(1)不难看出，薄膜具有的总弹性应变能为法向位移二阶空间倒数的函数，其一阶导数不连续。若对其二阶求导，可预测其倒数必然发散，即表面具有的弹性应变能趋于无穷。

因此，当超材料系统与声场发生共振时，有较多的声能在这些狭长区域被转化为薄膜的弹性应变能，进而使其达到“吸声”的效果。

图4[6]为吸声超材料的入射波和散射波的示意图。图4中物理量下标+、−分别代表吸声超材料的右侧区域和左侧区域；i和o分别代表入射波和反射波；k0为空气中的波矢。

图4 吸声超材料的入射波和散射波的示意图Fig.4 Schematic illustration of the incident and scattering process from a DMR unit

当声波入射方向垂直于薄膜吸声超材料表面时，吸声系数A与薄膜左端的入射声压pi−和透射声压po−，薄膜右端的入射声压pi+透射声压po+有关。在可听频率(20 Hz～20 kHz)下，可以认为膜厚度恒定即薄膜两侧无相对运动，则平均声压幅值守恒：

当吸声超材料左右均有声波入射时，总输入能量通量可以表示为，Z0为空气中的声阻抗。守恒的能量为能够被耗散的能量通量为，实际被吸收的能量为，那么吸声系数A可从从能量角度定义如下：

文中薄膜超材料在使用时只从一侧入射声波，pi+= 0。此时有Amax= 1/2，因此本文中薄膜超材料使用时只从一侧入射，单层薄膜吸声超材料的吸声系数不会超过0.5。

1.2 仿真结果及分析

1.2.1 质量非对称声学超材料的结构优化仿真分析

由于超材料的振动模态与质量片的质量有关，因此嵌有不同质量的薄膜的共振吸收峰对应的频率也将不同。将质量非对称型薄膜声学超材料置于声场中后，超材料不同部分的薄膜能够对不同频率的声波进行有效吸收，因此可以达到宽频范围内吸声的效果。

本文仿真部分的研究重点为探究超材料单胞中不同质量比的质量片对质量非对称薄膜声学超材料吸声性能的影响，并参考仿真结果优选性能最佳的结构进行进一步研究。

首先确定了两个吸声超材料样品的质量片的厚度，按照图2的分布顺序，两个吸声超材料质量片厚度1∼厚度8 依次为0.3 mm、0.4 mm、0.5 mm、0.6 mm、0.7 mm、0.8 mm、0.9 mm、1.0 mm 和0.5 mm、0.6 mm、0.7 mm、0.8 mm、0.9 mm、1.0 mm、1.1 mm、1.2 mm。每个超材料单胞中的质量比即厚度1/厚度2、厚度3/厚度4、厚度5/厚度6、厚度7/厚度8 依次为0.75、0.833、0.875、0.90 和0.833、0.875、0.9、0.917。不难看出样品2 各单胞质量比的分布较样品1更加密集。

图5 样品1 与样品2 各单胞吸声系数曲线Fig.5 The sound absorption coefficient curves of each cell in sample 1 and sample 2

利用有限元方法依次计算样品1、样品2 的四个超材料单胞吸声系数，结果如图5所示。由图5不难看出，样品2 在300～500 Hz处无共振吸收峰，而样品1 在该区域有且仅有一个共振吸收峰。前者单胞的共振吸收峰的分布情况相比后者更加均匀。

图6是样品1 和样品2 的整体吸声系数曲线图，也较为明晰地验证了质量比与吸声性能间的联系。但由于样品1在300～500 Hz内的共振吸收峰分布较200～300 Hz 依然较为稀疏，因此由图6不难发现其吸声系数曲线依然出现了明显的吸收谷。

基于以上发现，为进一步寻找最佳的优化方案，我们设计了a、b、c、d、e五个质量非对称型薄膜声学超材料样品，不同样品所拥有的质量片厚度不同，其他影响超材料吸声系数的因素均相同。各样品所使用的质量片厚度数值由表1示出。

图7展示了五个样品的吸声系数曲线。不难看出，样品a(0.1～0.8 mm)的吸声系数曲线最平稳，在100～1000 Hz范围内的吸声系数最优。

图6 样品1 与样品2 的整体吸声系数曲线Fig.6 Sound absorption coefficient curves of sample 1 and sample 2

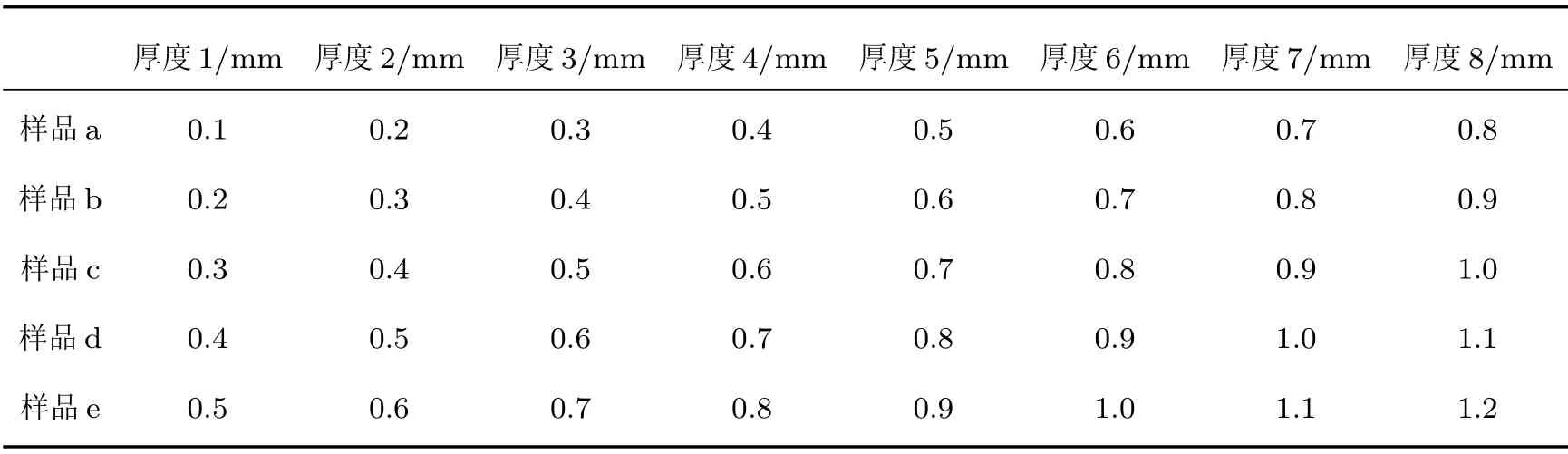
表1 各样品质量片的厚度Table1 Thickness of platelets on samples

图7 五个样品的整体吸声系数曲线Fig.7 Sound absorption coefficient curves of five samples

1.2.2 超材料的位移和能量仿真

图8是利用Comsol Multiphysics 有限元仿真软件对模型吸声系数进行仿真的结果。通过将其与质量对称结构的吸声系数曲线对比不难发现，质量非对称结构的共振吸收峰明显增多，且宽频范围内的平均吸声系数高于质量对称结构。

为进一步验证其吸声机理，本文将超材料置于声场中的位移云图和弹性应变能云图分别示于图9和图10中。

从图中不难看出，不同共振吸收峰频率对应着不同质量片的大幅振动，且大幅振动质量片的周围累积较多的弹性应变能，而与质量片距离较远的薄膜区域则几乎不累积弹性应变能。仿真结果与理论推测吻合良好。

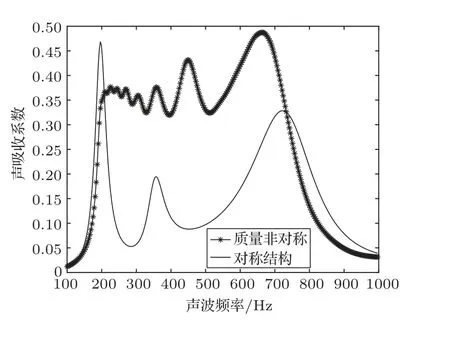
图8 对称结构与质量非对称结构仿真吸声系数曲线Fig.8 Sound absorption coefficient curve for symmetric structure and mass-asymmetrical structure

图9 厚度梯度质量非对称结构位移云图Fig.9 Displacement nephogram of asymmetric structure with thickness gradient mass

图10 厚度梯度质量非对称结构弹性应变能密度云图Fig.10 Energy density nephogram of asymmetric structure with thickness gradient mass

2 实验准备

薄膜声学超材料样品由薄膜、刚性底板和刚性质量片构成。其中，薄膜的材料为硅橡胶，材料密度为980 kg/m3，泊松比0.48，杨氏模量为0.2×109Pa，厚度为0.2 mm。底板和质量片均由4430 不锈钢材料制成，密度为7850 kg/m3,泊松比为0.28，杨氏模量为2.05×1011Pa。底板为圆形，直径为99.5 mm，质量片呈半圆形。

制备时需要先在圆形底板上加工出矩形边框，接着将薄膜在底板上张紧，使其中部区域的预应力大小及均匀程度满足实验需求，再使用硅胶将加工完成的底板与张紧的薄膜粘合。待胶凝固后，割去矩形边框外多余的薄膜。质量片按厚度梯度分布的形式粘合在矩形区域薄膜的表面。实验样品的直径略小于声学阻抗管的内径，因此需要在其四周粘贴一层弹性胶带，提高样品在阻抗管中固定的稳定性，并确保其在实验过程中便于安装和取出。样品实物如图11所示。

图11 实验样品Fig.11 Experimental sample

本实验系统主要由阻抗管、传声器、频率分析器、信号发生器、功率放大器以及扬声器组成，如图12所示。

实验中使用的声学阻抗管由声望公司生产，其型号为SW422。声管总长约为1.8 m，内径为99.8 mm，分为入射管和透射管两个部分。实验时样品需被放置在两管中间，并将两管中部卡紧，使其固定得足够稳定，且确保无漏声。阻抗管的吸声末端填充有一厚度为2 cm的圆盘状吸声海绵。

本次实验共制备两个实验样品，每个实验样品测试三次，实验结果取三次的平均值。

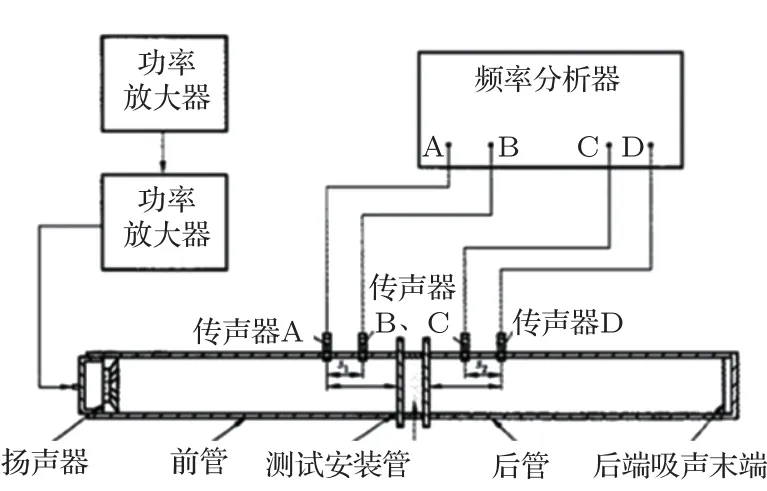
图12 测试系统示意图Fig.12 Test system diagram

3 实验结果分析

图13 中实验样品吸声系数曲线出现多个明显的共振吸收峰， 吸收峰频率范围集中在250∼800 Hz，与仿真中的200∼700 Hz 基本吻合。随着频率的升高，共振吸收峰峰值所对应的吸声系数也有所提高，这与仿真中的变化趋势类似。此外，实验样品在250～520 Hz 的低频范围内的平均吸声系数达到了0.33，部分共振吸收峰处的吸声系数达到0.45，接近单层薄膜超材料吸声最大值，实验样品达到了低频下宽频吸声的要求。

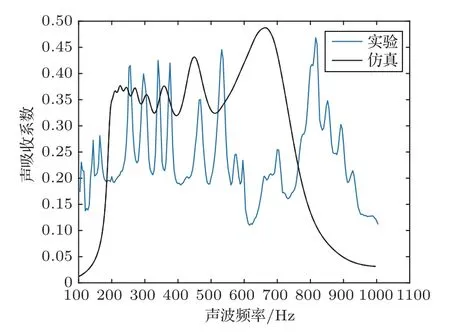
图13 实验吸声系数与仿真吸声系数曲线对比Fig.13 Comparison between experimental sound absorption coefficient curve and simulated sound absorption coefficient

图13 中，实验和仿真的吸声系数曲线存在差异，原因主要有以下几点：(1)金属片厚度误差，金属片厚度决定金属片质量，直接影响吸声频率的分布。由于金属片厚度0.1～0.3 mm有一定的加工难度，存在较大的加工误差，从而导致600∼800 Hz 范围对应的吸声系数与理论值有较大差距；(2)薄膜张紧误差；(3)试验中吸声系数的测量方式，薄膜声学超材料对声波频率变化敏感，更适合用单频声源逐频率依次测量，鉴于现有设备性能局限，未能采用单频声源逐频率测量。

通过将测试所得质量非对称薄膜声学超材料的吸声系数曲线和吸声海绵的吸声系数曲线对比，较常规吸声材料，质量非对称薄膜声学超材料有以下两点优势：首先，质量非对称薄膜声学超材料厚度小，样品的最厚区域仅为3 mm，而拥有较良好吸声性能的吸声海绵的厚度至少需要达到50 mm。其次，由图14 不难发现，质量非对称型薄膜声学超材料能够显著吸收100～1000 Hz范围内的低频声波，而吸声海绵的低频吸声能力则相对较差。

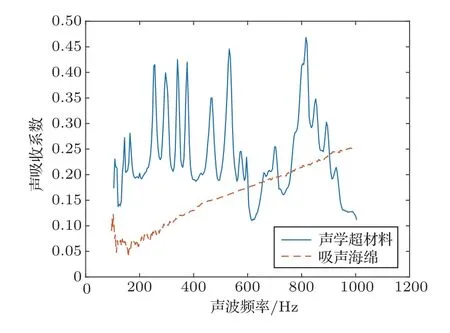
图14 薄膜声学超材料与吸声海绵吸声系数曲线对比Fig.14 Comparison of sound absorption coefficient curves between membrane sound-absorbing metamaterial and sound absorption sponge

4 结论

本文在传统吸声型薄膜声学超材料的基础上引入质量非对称结构，成功设计制作出拥有低频宽带吸声能力的薄膜声学超材料实验样品，并利用声学阻抗管测试系统对其吸声系数进行测试。测试结果与仿真结果显示出了较高的一致性。测试结果同时表明实验样品较吸声海绵拥有更加优良的低频宽带吸声性能。在今后的实验中，将设计专用夹具并改进实验设备进一步提高实验样品的制作和测试精度。