随钻声波测井圆弧状压电阵子的有限元分析∗

孙志峰 唐晓明 苏远大 陈洪海 仇 傲 李 杰

(1 中国石油大学(华东)地球科学与技术学院 青岛 266580)

(2 中海油田服务股份有限公司 北京 101149)

0 引言

随钻声波换能器是随钻声波测井仪器的核心部件，该技术目前制约我国随钻声波测井技术发展。传统的电缆声波测井仪器采用圆管换能器，利用其膨胀-收缩模态实现单极子声源发射，向井外地层辐射声波能量。而随钻声波测井仪器发射换能器需要安装在钻铤的凹槽内，由于机械安装的困难无法采用圆管换能器，通常把圆管换能器切割成均匀的四片圆弧状压电阵子，进行封装后安装在钻铤上，实现随钻单极子声源的发射[1]。圆弧状压电阵子由于切割的影响，其膨胀-收缩模态振动频率、频率响应、发射电压级等声学特性与圆管换能器有很大的差异。因此研究圆弧状压电阵子的声学性能对随钻发射换能器的设计具有参考价值。

吴金平等[2]制作了应用于随钻声波测井的圆弧状压电振子，并进行了声学性能实验研究。刘玉凯等[3]基于有限元法计算了钻铤存在对随钻多极子换能器水平指向性的影响。魏倩等[4]采用有限元法研究了三叠片圆形随钻换能器，分析了基片材料对其发射性能的影响。Fu 等[5]采用有限元分析方法对随钻声波换能器提出了优化设计方案，通过采用低阶弯曲振动模态的方式提高换能器的带宽及机电性能。陈俊圆等[6]采用有限元方法研究了适用于随钻方位测井的圆弧状声波发射换能器，考察了钻铤及换能器尺寸对声源谐振频率及水平指向性的影响。以上多数学者研究的随钻声波发射换能器均采用了圆弧状压电阵子，其声学性能决定随钻声波测井仪器的测量效果。

随钻声波测井仪一般设计几种不同尺寸的钻铤适应不同的井眼测量环境，因此需要对发射换能器的尺寸做优化设计，由于压电阵子采用的是圆弧状结构，因此很难用解析方法进行分析[7]。COMSOL Multiphysics 是一个基于高级数值方法，用于建模和模拟物理场问题的通用有限元分析软件，该软件在声波测井换能器设计及声场计算中有广泛的应用。本文采用COMSOL Multiphysics 有限元分析软件，数值模拟了圆弧状压电振子结构参数对其振动模态、谐振频率及发射电压级响应等因素的影响。

1 圆弧状压电阵子的有限元分析

1.1 圆弧状压电阵子的有限元模型

随钻声波测井仪发射换能器一般由四片圆弧状换能器组合而成，每片换能器采用环氧树脂等材料对圆弧状压电阵子进行封装，最外层再用橡胶进行封装。由于四片圆弧状压电阵子具有结构对称性，声学性能完全一致，因此仅需研究单片压电阵子的声学性能。另外由于压电振子是换能器辐射声波的核心部件，因此文本的数值模拟不考虑封装材料等因素的影响。

图1为圆弧状压电阵子结构简图。压电振子的高度H为40 mm，厚度D为5 mm，半径R为77 mm，张开角α为80◦。压电振子采用PZT-5A且厚度方向极化的压电陶瓷片。数值模拟中压电阵子采用自由边界条件。压电振子的内外表面分别施加正负电压，在外加电压信号的激励下，圆弧状压电阵子可产生弯曲振动或径向振动等模态，进而向外辐射声波能量。

图1 圆弧状压电阵子结构示意图Fig.1 Structure of arcuate shaped piezoelectric vibrator

1.2 圆弧状压电阵子的振动模态分析

在COMSOL Multiphysics 软件固体力学模块中选择压电设备物理场接口，利用特征频率研究方法可对压电设备进行模态分析。数值计算表明圆弧状压电阵子的振动模式非常丰富，主要存在弯曲振动模态及径向振动振动模态，不同的振动模态可分别用于随钻单极子、偶极子或四极子测量模式。

图2分别为圆弧状压电阵子的两种主要振动形态图。从图2(a)可以看出，圆弧状压电阵子在谐振频率为1.373 kHz 处存在弯曲振动模态，压电阵子在环向上产生弯曲振动；从图2(b)可以看出，圆弧状压电阵子在谐振频率为14.589 kHz 处存在径向振动模态，该模态类似于圆管换能器的膨胀-收缩模态。随钻声波测井单极声源激发频率范围为10 kHz～20 kHz，因此圆弧状压电阵子的径向振动模态可用于随钻单极子测量模式。而随钻偶极子或四极子激发频率范围为1 kHz～8 kHz，因此环向弯曲振动模态可用于偶极子或四极子测量模式。

图2 圆弧状压电阵子的振动模态Fig.2 Vibration mode of arcuate shaped piezoelectric vibrator

1.3 圆弧状压电阵子的频响特性分析

在COMSOL Multiphysics 软件结构力学模块中选择压电设备物理场接口，利用频域研究方法可对压电设备进行频响特征分析。对圆弧状压电阵子施加1 V 的正弦电压，可以得到压电阵子在空气中的导纳特性曲线，如图3所示。从图中可以看出，圆弧状压电阵子径向振动谐振频率为14.6 kHz，对应的电导值为2.33 mS，表明压电阵子的径向振动模态具有良好的机电转换性能。而圆弧状压电阵子在环向弯曲振动模态的谐振频率点附近无明显变化，表明这种模式的机电转换效率较差。

图4是圆弧状压电阵子在频率为14.6 kHz处的振动位移矢量图。从图中可以看出，压电阵子的中部位移矢量均沿径向方向，径向位移最大；压电阵子的两端位移矢量主要沿切向方向，径向位移很小。

图3 圆弧状压电阵子在空气中的导纳曲线Fig.3 Admittance curve of arcuate shaped piezoelectric vibrator in the air

图4 圆弧状压电阵子振动位移矢量图Fig.4 Displacement vector of arcuate shaped piezoelectric vibrator

图5是圆弧状压电阵子在频率为14.6 kHz 处，不同位置处三个方向上的位移分布。从图中可以看出，压电阵子的径向位移、切向位移沿中心点呈对称分布。压电阵子中心部位径向位移最大，且向两端逐渐递减，两端端点处径向位移趋近于零；压电阵子中心部位切向位移为零，且向两端逐渐递增，两端端点处切向位移最大；压电阵子任意点的轴向位移接近于零。

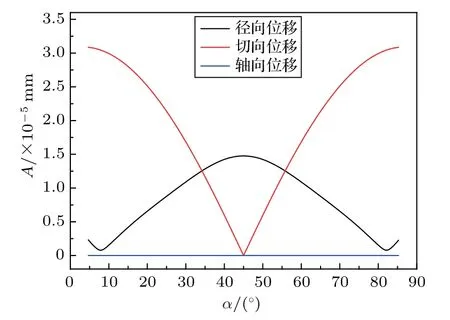
图5 圆弧状压电阵子的位移分布Fig.5 Displacement distribution of arcuate shaped piezoelectric vibrator

1.4 圆弧状压电阵子的发射电压级响应

在COMSOL Multiphysics 声学模块中选择声-压电相互作用物理场接口，利用频域研究方法可对压电设备进行发射电压级响应计算。对圆弧状压电阵子在流体域中建立几何模型，流体域为半径200 mm的球体，流体为水。为了保证换能器的激发声场在球域边界没有反射，需在球域设置厚度为40 mm的完全匹配层。对压电振子的内外表面施加1 V 的正弦电压信号，可计算声轴上满足远场条件的某点声压，利用发射电压级计算公式[8−9]计算得到圆弧状压电阵子的发射电压级响应曲线如图6所示。从图中可以看出，频率为13.9 kHz 处对应最大发射电压级幅度为137.9 dB。该频率为圆弧状压电阵子在流体中的径向振动模态谐振频率，由于流体负载作用的影响，该谐振频率略低于压电阵子在空气中的径向振动谐振频率。

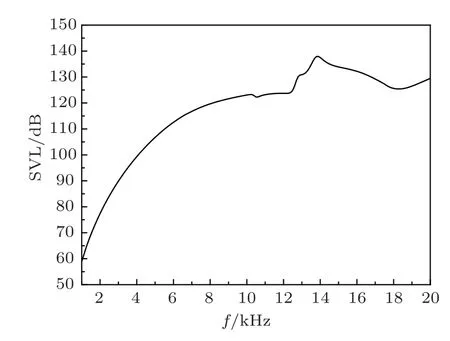
图6 圆弧状压电阵子的发射电压级响应Fig.6 Emission voltage level of arcuate shaped piezoelectric vibrator

2 结构尺寸对圆弧状压电阵子性能影响

圆弧状压电阵子结构参数对其声学性能的影响很大，影响因素主要有压电阵子厚度、高度、半径及张开角，随钻发射换能器设计需要综合考虑各种结构参数的影响，设计满足随钻测量环境的换能器。接下来在不改变圆弧状压电阵子基本结构的前提下，通过改变压电阵子的其中一个参量，分析压电阵子声学性能的变化趋势。

2.1 晶体厚度对压电阵子性能的影响

考察压电振子厚度变化对其声学性能指标的影响。模型中压电振子的高度H为40 mm，半径R为77 mm，张开角α为80◦，厚度D分别为2 mm、4 mm、6 mm、8 mm，其他参数保持不变。图7是不同厚度压电振子的性能变化图。其中，图7(a)为不同厚度圆弧状压电阵子在空气中的电导特性变化曲线，图7(b)为不同厚度压电阵子的发射电压级响应曲线。从图7中可得到不同厚度的压电振子的谐振频率、最大电导值及最大发射电压级幅值如表1所示。从表1中可以看出，随着压电阵子厚度增大，压电阵子径向振动模态的谐振频率逐渐向高频移动，电导值逐渐减小，压电阵子的最大发射电压级逐渐降低。

图7 不同厚度压电振子的性能变化Fig.7 Acoustic performance of piezoelectric vibrator with different thickness

表1 不同厚度压电振子的谐振频率、最大电导值及最大发射电压级幅值Table1 Resonance frequency,maximum conductance and maximum emission voltage level of piezoelectric vibrator with different thickness

2.2 晶体高度对压电阵子性能的影响

考察压电振子高度变化对其声学性能指标的影响。模型中压电振子的厚度D为5 mm，半径R为77 mm，张开角α为80◦，高度H分别为40 mm、50 mm、60 mm、70 mm，其他参数保持不变。图8是不同高度压电振子的性能变化图。其中，图8(a)为不同高度圆弧状压电阵子在空气中的电导特性变化曲线，图8(b)为不同高度压电阵子的发射电压级响应曲线。从图8中可得到不同高度压电振子的谐振频率、最大电导值及最大发射电压级幅值如表2所示。从表2中可以看出，随着压电阵子高度增大，压电阵子的径向振动模态的谐振频率逐渐向低频移动，电导值先增大后逐渐减小，压电阵子的最大发射电压级幅值先升高后逐渐降低。

图8 不同高度压电振子的性能变化Fig.8 Acoustic performance of piezoelectric vibrator with different height

表2 不同高度压电振子的谐振频率、最大电导值及最大发射电压级幅值Table2 Resonance frequency,maximum conductance and maximum emission voltage level of piezoelectric vibrator with different height

2.3 半径对压电阵子性能的影响

考察压电振子半径变化对其声学性能指标的影响。模型中压电振子的厚度D为5 mm，高度H为40 mm，张开角α为80◦，半径R分别为60 mm、70 mm、80 mm、90 mm，其他参数保持不变。图9是不同半径压电振子的性能变化图。其中，图9(a)为不同半径圆弧状压电阵子在空气中的电导特性变化曲线，图9(b)为不同半径压电阵子的发射电压级响应曲线。从图9中可得到不同半径压电振子的谐振频率、最大电导值及最大发射电压级幅值如表3所示。从表3中可以看出，随着压电阵子半径增大，压电阵子径向振动模态的谐振频率逐渐向低频移动，电导值逐渐增大，压电阵子的最大发射电压级幅逐渐升高。

图9 不同半径压电振子的性能变化Fig.9 Acoustic performance of piezoelectric vibrator with different radius

表3 不同半径压电振子的谐振频率、最大电导值及最大发射电压级幅值Table3 Resonance frequency,maximum conductance and maximum emission voltage level of piezoelectric vibrator with different radius

2.4 张开角度对压电阵子性能的影响

考察压电振子张开角变化对其声学性能指标的影响。模型中压电振子的厚度D为5 mm，高度H为40 mm，半径R为77 mm，张开角α分别为70◦、75◦、80◦、85◦，其他参数保持不变。图10是不同张开角压电振子的性能变化图。其中，图10(a)为不同张开角圆弧状压电阵子在空气中的电导特性变化曲线，图10(b)为不同张开角压电阵子的发射电压级响应曲线。从图10 中可得到不同张开角压电振子的谐振频率、最大电导值及最大发射电压级幅值如表4所示。从表4中可以看出，随着压电阵子张开角增大，压电阵子的径向振动模态的谐振频率逐渐向低频移动，电导值逐渐增大，压电阵子的最大发射电压级幅值逐渐降低。

表4 不同张开角压电振子的谐振频率、最大电导值及最大发射电压级幅值Table4 Resonance frequency,maximum conductance and maximum emission voltage level of piezoelectric vibrator with different opening angle

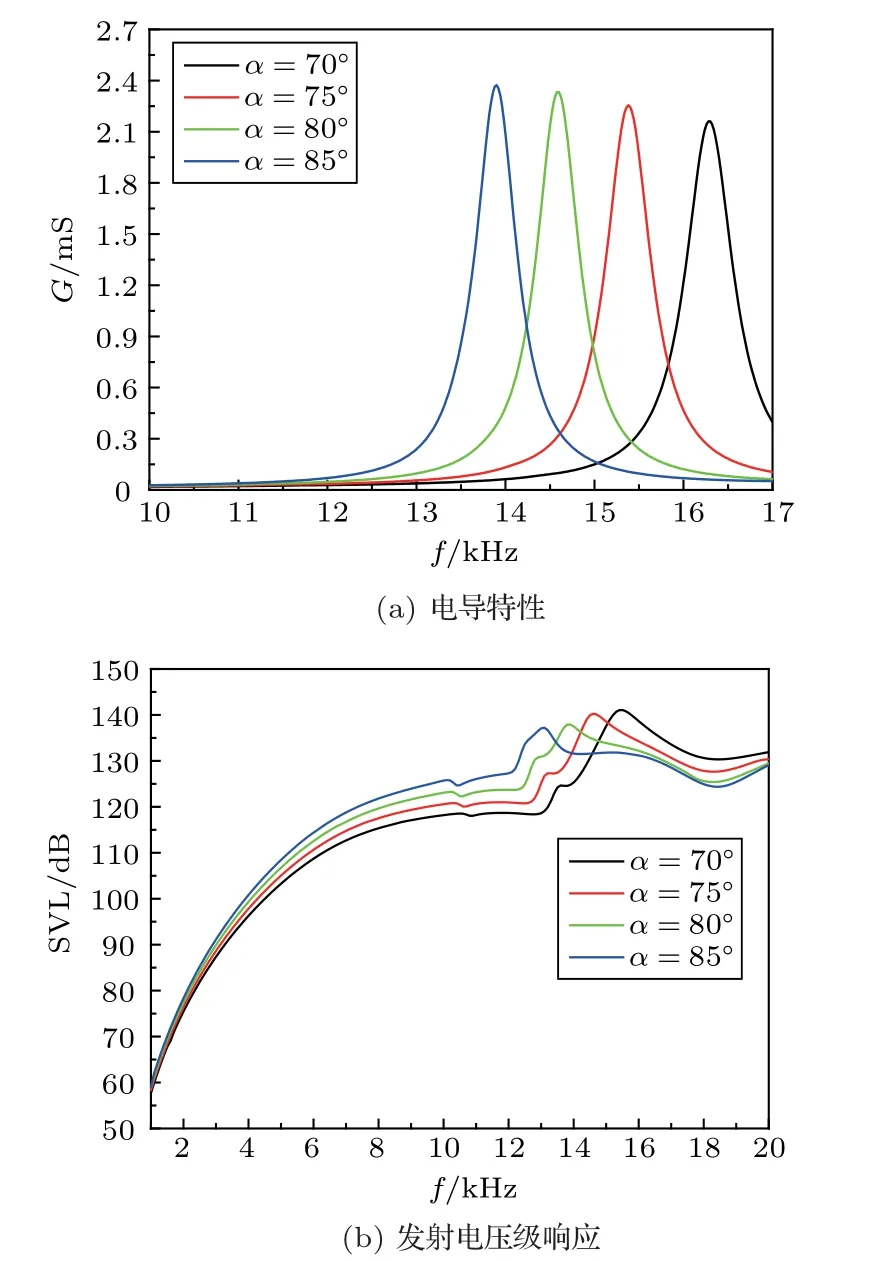
图10 不同张开角压电振子的性能变化Fig.10 Acoustic performance of piezoelectric vibrator with different opening angle

3 圆弧状压电阵子的优化设计

随钻声波测井仪测量时由于钻头尺寸不同，需要设计几种不同尺寸的工具以适应不同的井眼环境条件，如斯伦贝谢公司研制的SonicScope 随钻多极声波测井仪设计[10]采用了4.75 in、6.75 in 及8.25 in 三种不同尺寸外径的钻铤；另外由于钻铤的外径不同，钻铤模式波的隔声阻带也有差异[11]，需要发射换能器的谐振频率工作在隔声阻带频率范围内，才能保证尽量消除钻铤模式波对地层波信号的影响。因此需要优化设计晶体尺寸使发射换能器具有最大发射效率，满足随钻声波恶劣环境的测量需求。

本文以外径为6.75 in 钻铤为例阐述圆弧状压电阵子晶体尺寸的优化设计方法。6.75 in 的钻铤外半径为85.7 mm，由于换能器安装在钻铤凹槽内，换能器的半径不宜超过钻铤外径尺寸，另外考虑晶体封装材料的厚度，所以圆弧状压电阵子晶体的半径R为83 mm。由本文第2.4 节张开角对压电阵子性能影响因素可知，晶体张开角度越大，其电导值和发射电压级越高，另外考虑换能器两端的封装材料尺寸影响，圆弧状压电阵子晶体的张开角度α为85◦。下面同时改变圆弧状压电阵子的厚度及高度参数，研究其径向振动模态的谐振频率及最大电导值变化规律。圆弧状压电阵子的厚度D从2 mm到8 mm 变化，变化步长为1 mm，高度H从40 mm到70 mm 变化，变化步长为5 mm，采用COMSOL Multiphysics 软件中的参数扫描计算方法，可以一次性计算压电阵子任意厚度及高度组合参数的电导特性曲线。图11是不同尺寸压电振子的性能变化图。其中，图11(a)为不同厚度及高度压电阵子的径向振动谐振频率。由图11(a)可见，圆弧状压电阵子的厚度D为2 mm，高度H为70 mm 时，径向振动的谐振频率存在最小值为12365 Hz；圆弧状压电阵子的厚度D为8 mm，高度H为40 mm 时，径向振动的谐振频率存在最大值为13106 Hz。图11(b)为不同厚度及高度压电阵子的最大电导值。由图11(b)可见，圆弧状压电阵子的厚度D为2 mm，高度H为55 mm时，压电阵子的存在最大电导值为9.86 mS。

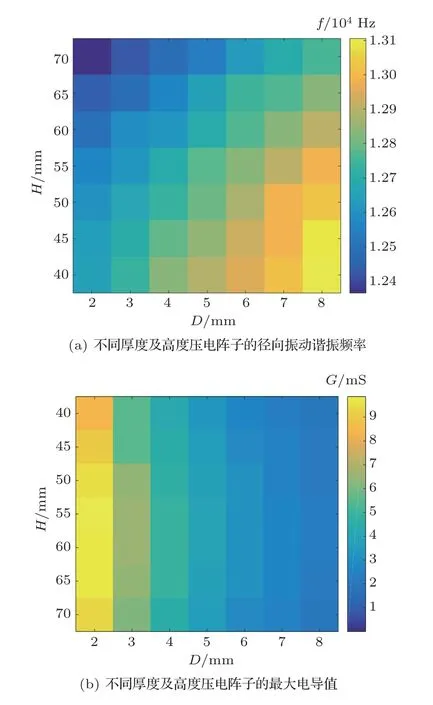
随钻声波测井仪一般采用刻槽的方式消除钻铤模式波的影响，不同的刻槽结构钻铤的隔声阻带的频率范围略有差异，一般外径为6.75 in 钻铤的隔声阻带中心频率约为13 kHz，发射换能器的径向振动谐振频率工作在该频率附近，测量信号中钻铤模式波对地层波的影响越小[12]。若某随钻声波测井仪钻铤的隔声阻带中心频率为12.8 kHz，由图11(a)可见，多种的厚度与高度组合均满足该谐振频率值，但是结合图11(b)使换能器具有最大的电导值，那么最优的圆弧状压电阵子厚度应为5 mm 或6 mm，高度为55 mm，该尺寸的圆弧状压电阵子径向振动谐振频率既满足隔声阻带中心频率的要求，同时又保证其有最大的发射电压级。

4 结论

本文采用有限元方法数值模拟了随钻声波测井圆弧状压电阵子的振动模态、频率响应及发射电压级响应，详细讨论了压电阵子几何尺寸的变化对其声学性能的影响。研究结果表明，一定频带范围内压电阵子存在多个振动模态，其中径向振动模态可以满足随钻声波测井仪单极子工作频率的要求，且发射电压级幅值较高。圆弧状压电阵子的性能参数受几何尺寸的改变影响较大。压电阵子的径向振动模态谐振频率随着陶瓷片厚度的增大而升高；随着陶瓷片高度、半径及张开角的增大而降低。最大电导值随着陶瓷片厚度的增大而减小；随着半径、张开角的增大而增大；随着陶瓷片高度的增大，电导值先增大后逐渐减小。最大发射电压级幅值随着陶瓷片厚度、张开角的增大而降低；随着半径的增大而升高；随着陶瓷片高度的增大，最大发射电压级幅值先升高后逐渐降低。在对不同外径的随钻声波发射换能器设计的时候，需要采用最优化设计方法，优化设计压电阵子几何尺寸，使谐振频率既满足随钻声波测井仪隔声阻带频率的要求，又保证发射换能器具有最大的声辐射效率。