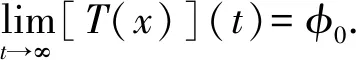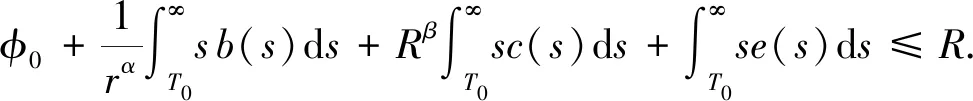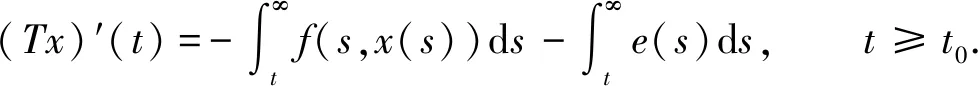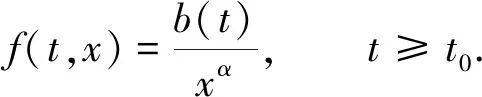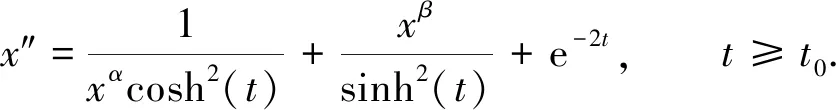带有渐近条件奇异微分方程的有界解

赵 进

(河海大学 理学院,南京 210098;扬州工业职业技术学院 基础科学部，江苏 扬州 225100)

0 引 言

考虑如下二阶奇异微分方程:

x″=f(t,x)+e(t),t≥t0∈,

(1)

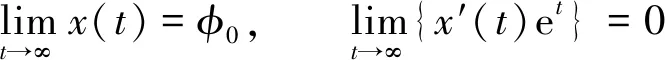
(2)

在物理学上更有意义,其中φ0>0是正常数.

Constantin等[1]利用流函数的形式建立了海洋环流运动的数学模型,并将其转化为如下一个半线性椭圆方程进行了研究:

(3)

Chu[2-4]借助文献[1]导出的模型,运用镜像对称变换和指数变换,将方程(3)转化为如下二阶常微分方程:

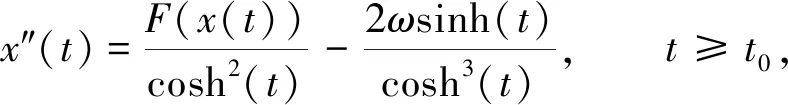
(4)

以及渐近条件

(5)

并对涡度函数F在常数、Lipschitz连续、一般非线性连续的情形下进行了系统研究.此外,关于奇异微分方程有界解的存在性研究也引起广泛关注,其中包括奇异周期问题[5-7]、奇异Dirichlet问题[8-9]等.常用的方法包括上下解、度理论和不动点定理.但目前已有的结果边界条件大部分是周期边界条件或其他分离边界条件.本文主要考虑方程(4)的一般形式,并从物理学的角度增加相应的渐近条件(2),根据Schauder不动点定理证明方程(1)-(2)有界解的存在性.

1 预备知识

为了能运用Schauder不动点定理,先把方程(1)-(2)转化成其等价的积分方程.事实上,若x(t)是方程(1)-(2)的解,则可得

(6)

此外,

其中需要假设条件

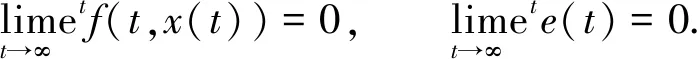
(7)

若满足式(6)的第二个条件,则对于任意的t∈[t0,+∞),可得

(8)

本文用Schauder不动点定理[10]证明积分方程(6)至少存在一个正的有界解.

2 主要结果

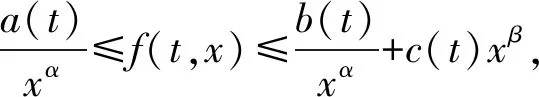
(9)

其中对于所有的t∈[t0,+∞),均有a(t),b(t),c(t)>0,且α,β>0.对于每个φ0>0,均存在T0≥t0,使得积分方程(6)至少有一个正的有界连续解x: [T0,∞)→,且满足

证明：设所有有界函数x∈C([T0,∞),)组成的集合为Banach空间X,定义

X1={x∈C([T0,∞),

(10)

这里

Ω={x∈X1: 0

其中r=φ0>0.

根据

可以证明算子T:Ω→X.此外,由

(11)

下面将应用Schauder不动点定理证明算子T在非空有界闭凸集Ω中至少有一个不动点,证明过程分三步.

1) 首先证明T(Ω)⊂Ω.对于每个x∈Ω和t≥T0,由于f和e都是非负的,可得(Tx)(t)≥φ0=r>0.根据不等式(11),有

因此,对于所有的t≥T0,有r≤(Tx)(t)≤R,从而算子T:Ω→Ω是可以定义的.

2) 证明T(Ω)在X中是相对紧的.根据Arzela-Ascoli定理,需证明T(Ω)是一致有界、等度连续和等度收敛的.令{xn}是Ω中一组任意的数列.

① 证明{Txn}在X中是一致有界的.显然,对于所有的t≥T0,有

② 证明{Txn}在X中是等度连续的.将算子(10)两边对t同时求导,可得

(12)

根据式(11),(12),对于所有的t≥T0,有

因此,对于所有的x∈Ω,有

|(Tx)′(t)|≤M,t≥T0,

其中

若{xn}是Ω中一组任意的数列,则

|(Txn)′(t)|≤M,t≥T0,n≥1.

应用中值定理,有

|(Txn)(t1)-(Txn)(t2)|≤M|t1-t2|,t1,t2≥T0,n≥1,

从而{Txn}在X中是等度连续的.

③ 证明{Txn}在X中是等度收敛的.根据

可得

即对于每个ε>0,均存在Tε>T0,使得

|(Txn)(t)-φ0|≤ε,t≥Tε,n≥1.

从而{Txn}在X中是等度收敛的.

3) 证明算子T:Ω→Ω是连续的.对一个给定的正常数ε,均存在T*≥T0,使得

由于f: [t0,T*]×[r,R]→是一致连续的,故存在一个正常数δ,使得对任意的x,y∈[r,R],且满足|x-y|<δ,均有

因此,对所有的x1,x2∈Ω且‖x1-x2‖<δ,有

由不等式

可得‖Tx1(t)-Tx2(t)‖<ε.所以算子T:Ω→Ω是连续的.

综上,算子T:Ω→Ω满足了Schauder不动点定理的所有假设条件.这里存在x∈Ω,使得T(x)=x,从而证明了积分方程(6)至少有一个边界解x: [t0,∞)→,且满足

由定理1可得：

推论1若方程(1)的非线性项满足

例1考虑如下奇异微分方程:

(13)

证明：通过计算易得

由于

于是,有

通过计算可得方程(13)解的形式,即

显然,对于t≥t0,均有x(t)>φ0.另一方面,由于

(责任编辑：李 琦，赵立芹)