无穷大树法解析哥德巴赫猜想
2019-11-27杨哲
【摘 要】采用“表达偶数与两素数间内在关系的无穷大树法”解析哥德巴赫猜想的“1+1”。
【关键词】哥德巴赫猜想;陈景润;无穷性;随机性;无穷大树法
一、引言
陈景润论文[1]称证明了“1+2”,文献[2]证明了“1+1”,本文意在解析猜想的“1+1”。
二、定理
定理1:任意一个大于2的偶数都可以表示为两个素数之和。
表达式:2n=p1+p2(1
定理2:任意一个大于2的偶数都可以表示为两个素数之和,且当偶数大于12时这样的两素数存在一对以上,偶数越大这样的两素数越多(波浪式增多)。
表达式:2n=p11+p21=p12+p22=…=p1i+p2i
定理3:任意一个大于2的偶数2n都可以表示为两素数p1,p2之和,且p1,n,p2成等差数列,其中的n是等差中项。
表达式:2n=p1+p2或n-p1=p2-n
说明:定理2及定理3是定理1的两个不同的拓展。
三、无穷大树结构
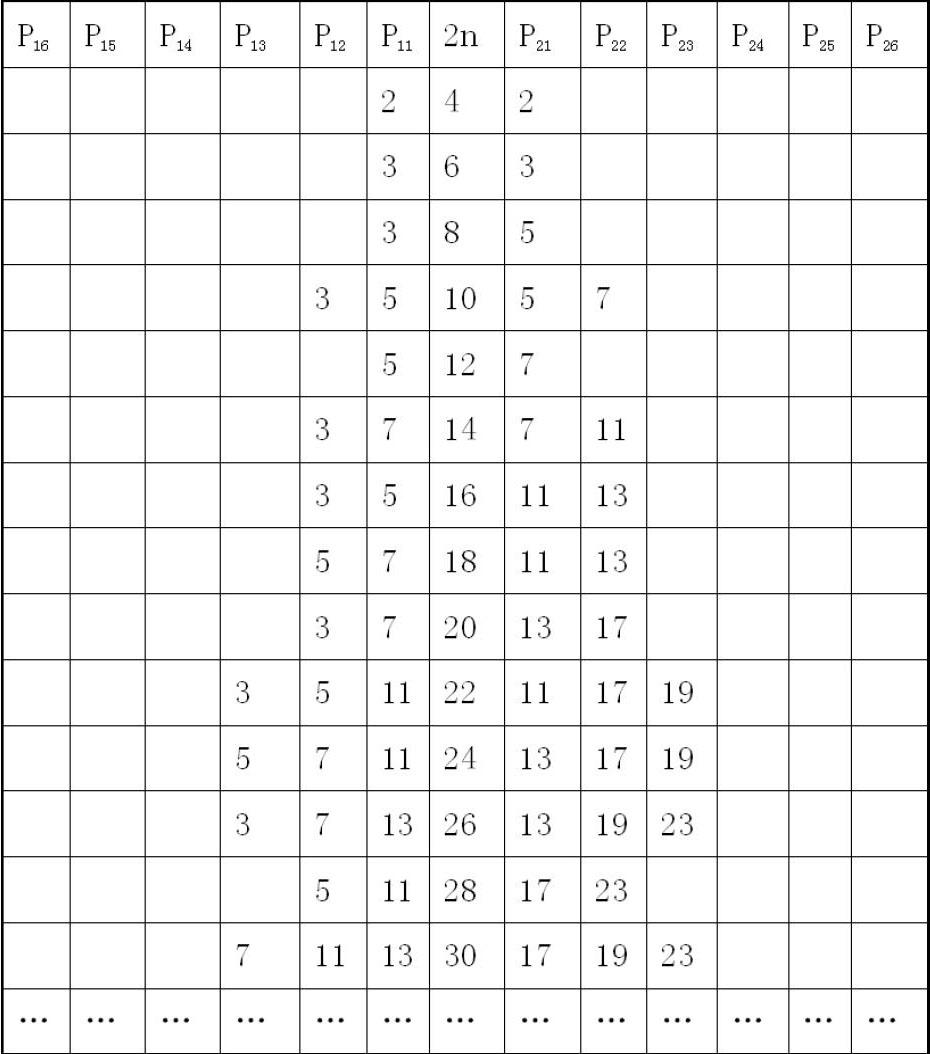
参照表1:以无穷多偶数2n为树的主干,以无穷多两素数p1i,p2i为树的左右侧枝。
例如:偶数4,6,…,26位于表1中间一列为无穷大树的“主干”,相对应的两素数位于表1中偶数两侧成为“侧枝”,两素数的和与偶数分别一一对应相等。
2…4…2;3…5…10…5…7.;3…5…16…11…13;.…3…11…22…11…19……;
3…6…3;.…5…12…7……;5…7…18…11…13;5…7…11…24…13…17…19;
3…8…5;3…7…14…7…11;3…7…20…13…17;3…7…13…26…13…19…23.
四、无穷大树计算
计算方法:每一个偶数为每一对两素数的对称中心,依次由内向外一一计算。
计算公式:2n=p11+p21=p12+p22=…=p1i+p2i(1
例如:
1个素数对:4=2+2,6=3+3,8=3+5,12=5+7
2个素数对:10=5+5=3+7,14=7+7=3+11,16=5+11=3+13,
18=7+11=5+13,20=7+13=3+17
3个素数对:22=11+11=5+17=3+19,24=11+13=7+17=5+19,
26=13+13=7+19=3+23.
偶数增大,与之对应的两素数逐渐增多(波浪式增多)。
五、无穷大树意义
偶数与素数的无穷多性决定了无穷大树的无穷大性,每一对的两素数关于每一个偶数的对应性决定了无穷大树的随机性。无穷大性及随机性,使得无穷大树具有下列意义。
表达猜想:无穷大树可以表达哥德巴赫猜想的“1=1+1”,即可以表达:“任意一个大于2的偶数都可以表示为两个素数之和。”
解析定理1:对于任一大于2的偶数,都可在无穷大树左右侧枝上各找到一个合适的素数,使两个素数的和与这个偶数相等,满足哥德巴赫猜想“1+1”。
解析定理2:对于任一大于12的偶数,都可在左右侧枝各找到2个或2个以上的素数组成多个素数对,使每个素数对的和都与这个偶数相等,且素数对成波浪式增多。
解析定理3:对于任一大于2的偶数2n,都至少可以在无穷大树的左右侧枝各找到1个素数组成1个素数对,使得素数对都与n成为等差数列,其中n是等差中项。
验证猜想:根据计算公式由内向外一一对应计算,可以验证哥德巴赫猜想。
六、无穷大树形表
表1:中间一列偶数2n为树的主干,左右两侧各一个素数组成相对应的素数对p1i,p2i为树的侧枝,而且侧枝随著主干的增长成波浪式增长。计算公式:2n=p1i+p2i (同4).
【参考文献】
[1]陈景润,大偶数表为一个素数及一个不超过两个素数的乘积之和,中国科学(数学),
1973,03(2):111-128.
[2] 杨哲,论哥德巴赫猜想,智富时代,2018年第11期:303-306页.(龙源期刊网).
[3] 杨哲,证明哥德巴赫猜想,知识文库,2019,457(09):229+232.(中国知网).
