例谈数学教学中的延伸策略
2019-11-27谢玲玲
谢玲玲
数学教学中教师应重视培养学生的思维能力、创新意识和情感价值观,但仅通过教材的学习难以实现这些目标,因此教师要钻研教材,拓宽教材,适时地进行知识的延伸。延伸,是指在讲授新内容的基础上,将知识面拓宽、引申。这样做,既能开阔学生视野,丰富他们的知识和技能,又可培养他们的创新意识。下面笔者通过几个课堂教学实例来谈谈数学教学中的延伸策略。
一、解题方法的延伸
在八年级“分式”的复习课上,教师提出问题:等式[1x(x+1)=1x-1x+1]成立吗?学生很快用异分母分式的减法验证等式成立后,教師又依次出示题目:
例1计算:[1x(x+1)+1(x+1)(x+2)+…+][1(x+2018)(x+2019)]
例2 解方程: [1x(x+3)]+[1(x+3)(x+6)]+[1(x+6)(x+9)]=[32x+18]。
学生运用问题中的结论解答例1,在成功中激发了解题的兴趣,迫不及待地想做例2。这样的延伸让学生体会在学习中所获得的快乐,变被动学习为主动学习,大大激发了学习的兴趣。
二、开放性问题设计的延伸
开放性问题思考容量大,学有余力的学生在解题过程中表现出强烈的解题欲望,从而产生浓厚的学习兴趣。而学习有点吃力的学生也能从其他同学的解题中受到启发,提高解题能力。
在教学完“平行四边形的判定”后,教师设计了这样一道习题:在四边形ABCD中,添加两个条件,使四边形ABCD是平行四边形。这道题目看似简单,学生答案却多种多样、五花八门。他们积极思考,勇于发言,激活了解题思路,积极从不同的方向寻求答案。这样的延伸体现了教学的开放性和个性化,既有利于学生对“平行四边形判定方法”的掌握和巩固,又能使学生的思维越来越灵活,应变能力越来越强,且摆脱了模式化的禁锢、束缚。
三、巧用错误进行延伸
在教学中,我们常常会遇到这样或那样的错误,在这些错误问题的处理中,如果教师能随机应变、善对错误、抓住错误进行适时延伸,便会收到意想不到的效果。
在一次听课活动中,两个学生在黑板上板演同一道习题。
计算: [4(x+1)(x+2)]+[3(x+2)(x-1)]-[2(x+1)(x-1)]
甲:原式=[4(x-1)+3(x+1)-2(x+2)(x+1)(x+2)(x-1)]=[5x-5(x+1)(x+2)(x-1)]=[5(x+1)(x+2)]。
乙:原式=[4(x-1)+3(x+1)-2(x+2)=5x-5]。
师:谁的答案正确?
生(学生异口同声):甲。
师:谁来说说乙同学错误的原因?
生:他丢分母了。
师:你们对乙同学的答案做怎样的变通就能得到正确答案?
生:我知道了,用他的结论除以(x+1)(x+2)(x-1)就可以得到正确答案。
生:哇,我明白了。
教学中,我们在面对错误时,不是戛然而止,而应该适时延伸,讨论“错在什么地方?怎样改?有多少变通的方式?”这样既帮助学生纠正了错误,又提高了他们自主学习和解决问题的能力,让所学知识得以巩固和延伸,印象则更加深刻。
四、知识模型的延伸
在数学学习中,机械式的模仿是基础知识的原始应用,在这个基础上可发展学生思维,从而挖掘解题方法。例如,在学习几何图形中线段的最值问题时可进行下面知识模型的延伸:
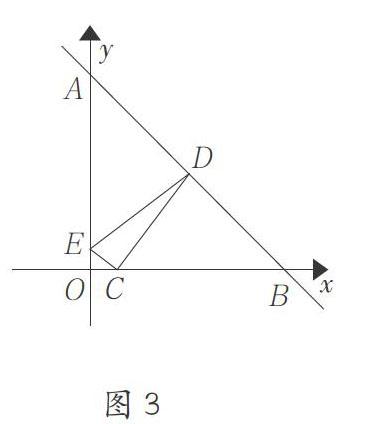
基本模型:如图1,在直线L上找一点P,使得PA+PB最小。
[A'][A][B][L]
图1
分析:作点A关于直线L的对称点A′,连接A′B交直线L于点P,则PA+PB的值最小,其依据是 。
解决问题:
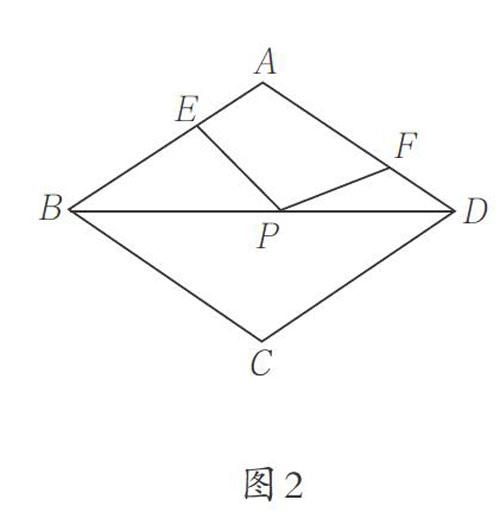
(1)如图2,在周长为12㎝的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 。
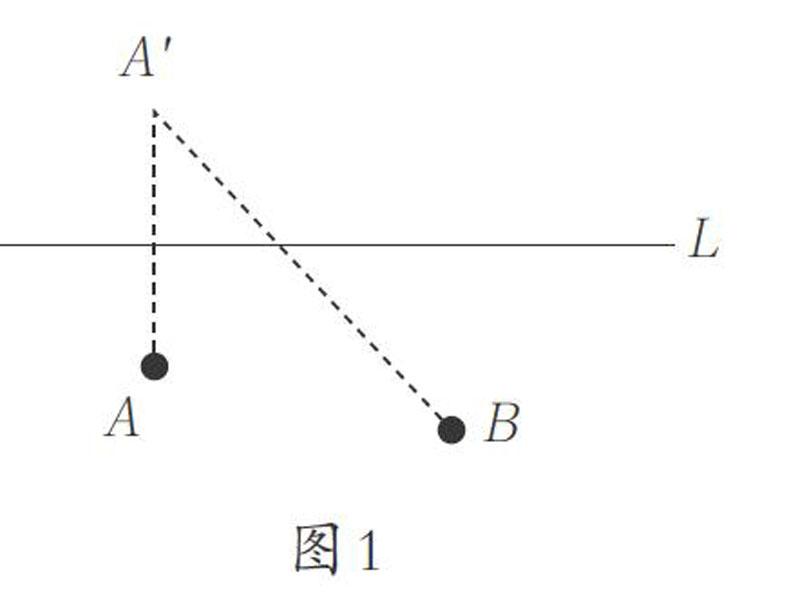
[A][E][B][P][D][F][C][A][D][E][O][C][B][x][y]
图2 图3
(2)如图3,已知C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,则△CDE周长的最小值是 。
问题(1)(2)与基本模型形异质同,它们只是基本模型的延伸,但解法相似。教学中能恰到好处地运用基本模型,就能顺利解决问题。
总之,数学教学中的延伸,不仅可以深化学生的数学思维,提高学生学习兴趣,更能为学生学习数学的可持续能力的发展夯实基础。但延伸必须看准新旧知识的生长点,必须顾及学生的认识水平和教学目标,切莫把延伸弄成不切实际的超前教育,否则就会本末倒置,适得其反。
(作者单位:江西省吉安市思源实验学校)
责任编辑 周瑜芽
E-mail:jxjyzyy@163.com
