回归学情视角： 让归纳推理学习真正发生

欧阳婷婷

培养儿童的归纳推理能力最根本的教学原则是要回归学情本位。学情永远是教学的“导航仪”和“指南针”。基于学情视角，我们会更加重视归纳推理教学中的学段差异、个体差别和体悟不佳等真实的教学问题。从真实的教学问题出发，我们才可能找寻出教学策略的全新路径。

一、追问：归纳推理教学的现状如何？

学情，顾名思义，是指学生学习的起点、状态和特点等。回归学情视角，我们不难发现：许多一线教师在归纳推理教学中忽视学情的现象比较普遍。

1.无视学段差异。学段不同，儿童的归纳推理能力必然会有差异。因为受思维水平、认知基础、学习方式等影响，各个学段儿童的接收、领悟能力差别很大，但许多教师在教学涉及归纳推理的课程内容时， 永远都采用“组织观察—引导比较—师生总结”的固定模式，缺乏深入细致的学情研究，“眉毛胡子一把抓”，使教学行为与真实学情“貌合神离”。

2.漠视个体起点。尽管我们一直强调备课要“备学生”，但在班级授课制的现状下， 很难做到“备到每一个学生”。尤其是在进行归纳推理教学时，我们很难切身体会每个学生的思维火花是如何闪耀的，他们的心弦是如何跳动的。更多情况下，我们只依据部分学生进行学情设计和实施教学，没提供兼容多样化学情的学习支架。这样使得优秀的学生依然优秀，后进的学生仍然后进，许多学生只能在原始水平层次停滞徘徊。

3.知识体悟不足。归纳推理是推理的一种重要形式，在小学阶段尤其是高年级，教师应该高度重视和培养学生对其严谨性的感悟。可是在教学中，很多教师因为小学数学的知识有限，所以大多数的归纳推理仅仅停留在举例验证层次上，没有上升到严谨完美的推理层次，学生认知始终停留在表面，体悟不深。

二、思考：归纳推理教学的基点何在？

教学行为，从它产生的那一天开始，其实质就指向“学”，而不是“教”。只有让每一个儿童的学习真正发生，归纳推理教学方可真正有效。《义务教育数学课程标准（2011年版）》明确指出：“推理是数学的基本思维方式，也是人们在学习和生活中经常使用的思维方式。”所以，回归学情视角，深度关注学生在归纳推理学习前、学习中和学习后的状态，应成为我们研究归纳推理教学的基点。

三、重构：归纳推理教学的策略在哪里？

1.面对不同学段：主攻不同层次的归纳推理能力。学段不同，儿童认知的最近发展区自然也不同。教师要寻找到归纳推理的能力层次与每个学段儿童最近发展区的最佳结合点，依据儿童学段层次，侧重培养儿童的不同能力。

（1）一二年级侧重培养儿童的观察能力。观察能力是进行归纳推理的重要基础。低段儿童的数学知识、思维能力和语言表达能力都相对匮乏，培养归纳推理的其他能力会很生硬。我们发现，一二年级的数学教材中有很多关于“数规律”和“形规律”的问题。观察这些数、形的排列特点，归纳其中的规律是每次数学活动的“标配”。所以，我们可以充分借助这些活动，重点培养学生的观察能力。

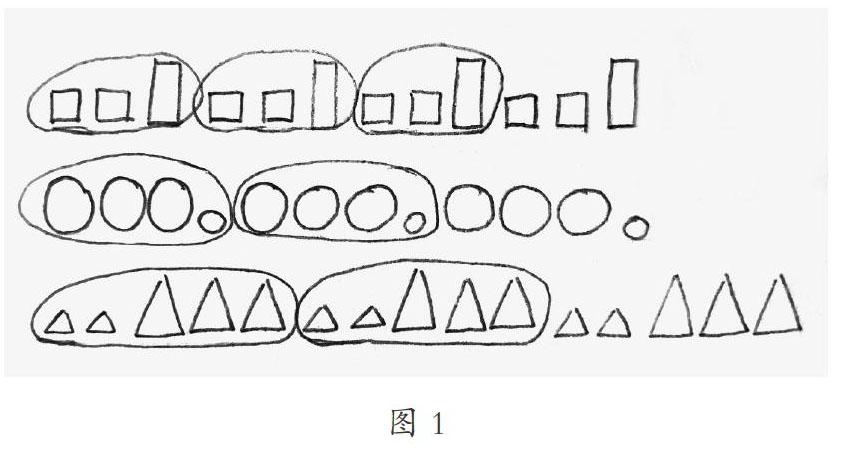
比如苏教版一年级（上）“分与合”练习中有这样一题（如图 1），这是学生第一次接触间隔排列，部分学生不容易发现其中的规律，这时教师引导学生学会观察方法至关重要。比如我们可以组织学生“数一数”“分一分”“说一说”等，然后鼓励学生“圈一圈”，再次观察比较，从而体会观察方法， 经历观察的过程，最终归纳出图形的排列规律。

图 1

（2）三四年级侧重培养儿童的猜想能力。儿童从诸多现象中形成猜想，是归纳推理的一个重要环节。面对三四年级的学生，教师培养他们在观察的基础上提出合理的猜想，应该成为培养归纳推理能力的一个阶段性重点。

比如苏教版四年级（下）“加法运算律”一课，教师与学生完成“加法交换律”和“加法结合律”学习后，补充一个环节：“根据今天的学习，你有什么大胆猜想吗？”现场有的学生猜想：“加法有交换律和结合律，那减法有没有呢？”“乘法有没有呢？”“除法呢？”面对精彩而合理的猜想，教师鼓励学生：“同学们的这些猜想都很合理，也很宝贵，说不定都是伟大的数学发现呢！”为什么要增加这个启发猜想的环节呢？因为一节课结束了不代表学生的思维活动就结束了，有了大胆猜想，哪怕是有瑕疵的猜想，他们也会用自己的方法去验证、推理、总结，从而把发展学生的推理能力延伸到课外。

（3）五六年级侧重让学生经历完整的归纳推理过程。归纳推理是一个很难用文字语言精确描述的思维过程，但其主要的思维过程是可以预见的，比如观察、比较、猜想、验证、表达等。对高年级学生而言，组织学生经历完整的归纳推理过程是形成他们归纳推理能力的重要策略。

“圆的周长”是苏教版五年级（下）的教学内容。教学中，教师组织学生根据教材情境，比较分析数据，提出合理的猜想：圆的周长是直径的 3 倍多一些。教师以此为契机， 请学生设计实验方案验证自己的猜想。学生经过组内交流，完善证明方法：“测量圆的周长，计算周长除以直径的商，分析比较数据，归纳圆周长计算公式”。 这个教学过程不但符合学生的真实学情，而且让学生比较完整地经历了归纳推理过程，真正感受到了“归纳推理过程全貌”，在學生的最近发展区提升了他们的归纳推理水平。

2.面对不同个体：搭建兼容性学习支架提升能力。苏霍姆林斯基说：“世界上没有抽象的儿童。”确实，每个教室里都没有两个完全一样的学生，每个学生都是不一样的，他们在学习过程中的差异是客观存在的。面对个体差异，我们要尽量给学生提供兼容性学习支架，帮助他们实现“不同的学生得到不同的发展”。

笔者在执教苏教版六年级（上）“正方体的展开图”一课中，就设计了兼容性的学习支架（大环节+好学具），引导学生归纳推理出正方体的展开图（如图2）。课上，学生明确展开图的含义后，笔者引导学生提出个性化的研究方向：如果沿着不同的棱剪开会不会得到不一样的展开图？是不是只要有6个正方形连起来就一定是正方体的展开图？正方体到底有多少种展开图？这些源自学生学情的真实问题成为这节课的核心问题。教学中，学生的想法很多，情绪高涨，操作规范，验证归纳的过程也非常精彩。

图 2

上述教学中，教师除了给学生提供统一的学具外，没有对归纳推理的过程做过多限制。学生设计归纳推理方案主要有两种，一种是由立体到平面，另一种是由平面到立体，代表了相反的思维方向，难易不同，但都有创造性，让归纳推理的过程可视化，实现了每个同学都有不同发展的教学目标。

3.面对知识体悟不足：丰盈归纳推理的说理支撑。在培养小学生的归纳推理能力时，如何突破“说起来重要，做起来次要”的教学窘境呢？现实教学中，教师首先要能正视小学的很多推理都是不完全归纳推理的“尴尬现状”，学生往往是半信半疑的真实感受;其次还应该设法通过说理的方式来支撑归纳推理的结论。学生只有真正感悟到了归纳推理是一个严密科学的过程，对归纳推理的领悟才会更加深刻。

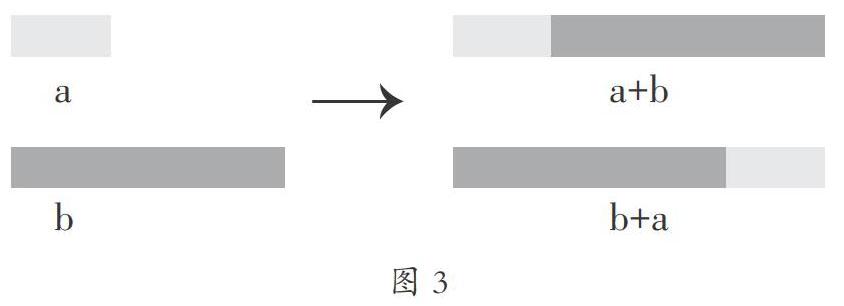
苏教版小学数学四年级（下）“加法运算律”这节课，教材上是通过举例验证， 引导学生总结出运算律的，但因为教材篇幅的限制，还是只停留在举例的层面。有学生就产生了质疑：“仅仅通过这 6 道题就可以得出加法交换律吗？怎么才能证明其他加法算式都符合这个规律呢？”面对这个疑问，教师如果不及时处理，学生就会质疑归纳推理的科学性，怎么办呢？教学中，笔者通过加法的意义来帮助学生进一步理解加法运算律，取得了良好的教学效果。用两根不同长度和颜色的彩条分别代表两个不同的加数 a 和 b（如图3），通过课件演示，同学们发现交换两根彩条的位置，彩条的长度和还是一样的，这种基于加法意义的说理支撑，毫无疑问让教材上的不完全归纳法真正获得了学生的认可。

教学，是一门需要教师终身探索的艺术。归纳推理学习的教学不容乐观，原因有很多：该内容在小学数学教材中的编排还不够完善，很多小学数学教师对归纳推理的认识不足，教学评价中对归纳推理能力考查的忽视和弱化，也有教学中偏离学情、忽视学情这个重要原因，所以回归真实学情，我们才能探寻到培养学生归纳推理能力的全新路径和教学策略，从而实现学生的推理能力高质量发展。

（作者单位：安徽省合肥市屯溪路小学）

责任编辑 周瑜芽

E-mail：jxjyzyy@163.com