用于捣固车道钉定位的磁力信号峰值检测算法*
2019-11-27吴海锋
高 萌,吴海锋,沈 勇,王 霞,曾 玉
(云南民族大学电气信息工程学院,昆明 650500)
对铁路中有砟道床进行捣固是将轨枕与道床之间的空隙捣实,使轨枕和铁轨受力均匀,道床平整密实,提高道床缓冲能力,从而确保铁路的安全运行。有砟铁路的捣固通常是由大型养路机械捣固车来完成,而捣固车在作业过程中需要提前确定下镐位置,定位一旦发生错误,镐头可能会损坏铁道和轨枕,甚至损坏捣固车[1-2],因此下镐定位是捣固作业中的重要环节。
传统的下镐定位采用人工方法,但作业强度大、效率低下,同时疲劳操作易造成作业失误。为了降低人工定位的操作强度,提高作业效率,近年来出现了多种自动定位方法。较为可行的是借助传感器实现自动下镐定位,由于传感器经过轨道扣件或道钉所产生的信号不同于其他元件的信号,因此轨道扣件可被识别,以此来确定下镐位置。常用的传感器定位有红外传感器、激光传感器和接触式传感器[2],但是它们仍然存在一定问题。红外传感器利用道钉与铁轨的不同温度来识别扣件,但是实际使用过程中两者的温差并不是很大;激光传感器中的光学仪器需要较干净的使用环境,以确保测量的有效性,但铁轨中多粉尘环境却难以保证这一条件;接触式传感器利用接触式开关来检测扣件,但该开关本身是一机械装置,其使用效果与扣件安装位置和具体形状密切相关,当扣件位置与开关不在同一水平面上或扣件本身损坏、缺失,检测性能也将受到影响。另外,计算机视觉技术也可应用于轨枕和扣件的识别[3-4],但该技术基于作业时所拍摄的图像,若拍摄光线昏暗或轨枕本身就被砟石覆盖,那识别工作也会变得困难。
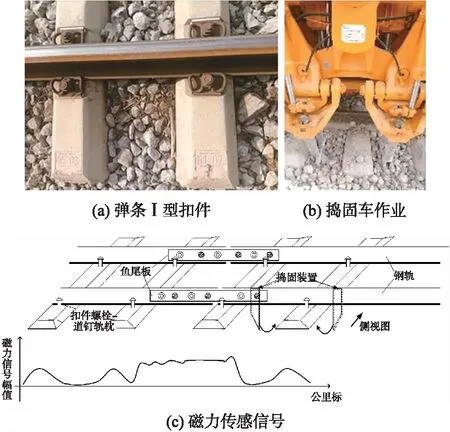
图1 弹条I型扣件轨道磁力传感信号示意图
由于以上传感器定位方法或多或少存在一定问题,我们考虑一种针对弹条式扣件轨道的多传感器联合定位系统。在该系统中,首先利用磁力传感器检测道钉或扣件,由于磁力传感器利用目标元件磁性变化的原理来进行检测,因此可减小遮挡、光照、温度、污损和接触不良等因素所带来的干扰,具有较强的环境适应性。磁力传感定位道钉问题其实是对磁力信号进行处理,其信号波形如图1所示。从图中可以看到,道钉位置对应的信号均为局部峰值点,检测到峰值信号即可找到对应的道钉,因此道钉定位问题可看作一道钉信号峰值检测问题。另外,图1所示的磁力信号还存在鱼尾板峰值信号。由于道钉信号被该信号所干扰,道钉难以被检测,需要将其去除,因此有效识别鱼尾板信号又是一个分类问题。此时,系统还需借助图像识别技术识别枕木,以此完成下镐定位。
本文主要针对该联合定位系统中磁力传感器道钉定位问题,研究一种有效、易行的峰值检测方法。在实验中,采用一组实测的磁力传感器道钉信号来评测本文方法,从漏检、假阳性和计算复杂度等方面将本文方法与传统方法作了对比,并给出了多组参数的实验结果。从实验结果看,当选用下采样、滑动窗检测、阈值分类和二次搜索方案来进行峰值检测时,漏检数和假阳性数可降为0,搜索次数为104量级,且最大道钉定位误差没有超过1 cm。
1 峰值检测算法研究
1.1 下采样处理
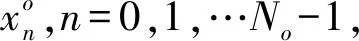
(1)
式中:Nd=⎣No/S」,⎣·」表示向下取整。
1.2 峰值检测
道钉的磁力传感器信号本质上是随距离变化的一维信号,且近似具有波谷到波峰再到波谷的规律,考虑采用滑动窗口法进行峰值检测,如图2所示。给定第w个长度L的可滑动矩形窗,窗口内序列为xw+0,xw+1,…xw+L-1,w∈{0,1,…Nd-L},若该序列中的最大值位于其中点处xw+|L/2|,则该中点就是一峰值点,表示为
xw+⎣L/2」∈A
(2)
当且仅当
xw+⎣L/2」>xw+i&xw+⎣L/2」>vthr
(3)
式中:A表示磁力传感器信号中所有峰值集合,i∈{0,1,…L-1},且i≠⎣L/2」,vthr为一阈值,以去除幅值较小的伪峰值点。相比传统的峰值检测算法,式(2)~(3)的窗口法仅需要通过几次比较就能找到峰值点,并不需要进行迭代或求目标函数。

图2 滑动窗口峰值检测图
此外,考虑到计算复杂度和漏检等因素,还需要对窗口长度L进行优化设置。减小L可以检测到更多的峰值点,理论上L=3就可确定xn为第n个采样点的峰值,只要满足xn-1
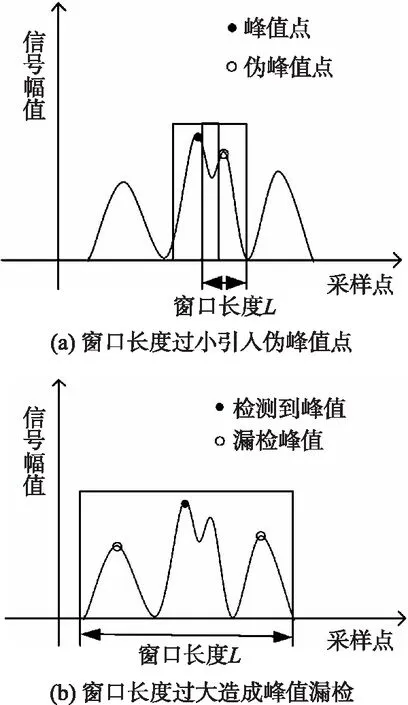
图3 窗口长度L对峰值检测的影响

图4 一道钉检测出多个峰值
1.3 重复检测
由于实际传感器信号受到噪声干扰,存在一个道钉可能对应多个峰值的现象。例如,道钉对应峰值点在短时间内退化成一直线,或变为多个峰值点,如图4所示。此时,可通过判断相邻峰值点的距离来检验是否为同一峰值,假定xn1,xn2为第n1和n2个采样点上检测到的相邻峰值,若
n1-n2≤Lthr
(4)
则认为该两个峰值点对应同一个道钉,其中Lthr表示距离的阈值。若式(4)满足,则表明一个道钉存在多个峰值点,为此还需确定最终峰值。令xn1,xn2,…xnK为一道钉对应的多个峰值点,若各峰值大小接近,最终峰值点位置可采用平均原则,表示为
(5)
若各峰值大小不一,可采用最大原则,表示为
(6)
1.4 峰值分类
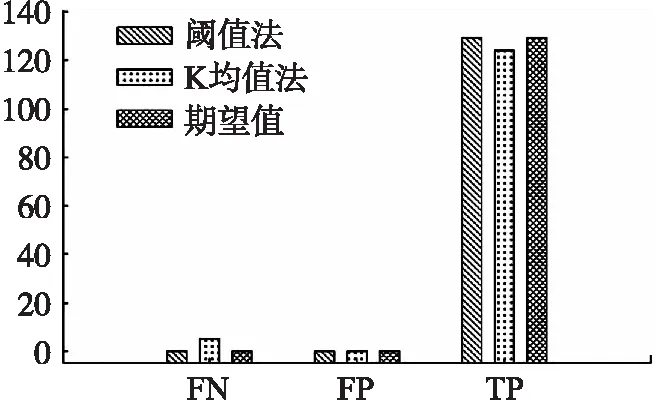
检测到的峰值可分为两类,一类对应道钉,一类对应鱼尾板,如图1所示。鱼尾板峰值信号将道钉峰值信息淹没,难以定位道钉,需要去除。一种可行的方法是用分类算法将鱼尾板信号去除,但分类算法首先要对分类对象提取特征值。主成分分析方法[5-7](Principal Component Analysis,PCA)可自动提取特征值,并实现特征的降维。我们可截取每段带有峰值的信号波形,利用PCA提取特征值,再用K均值[7-8]进行聚类。然而,K均值是一种无监督分类,计算复杂度一般较大。
此处,我们考虑用峰值大小作为特征值来进行分类。通常,鱼尾板的体积和重量均大于道钉,因此会产生更强的磁力感应信号,如图1所示,鱼尾板信号幅值要远大于道钉信号,因此用峰值大小作为特征值具有其合理性。令xn为在第n个采样点上的峰值,那么有
xn∈At
(7)
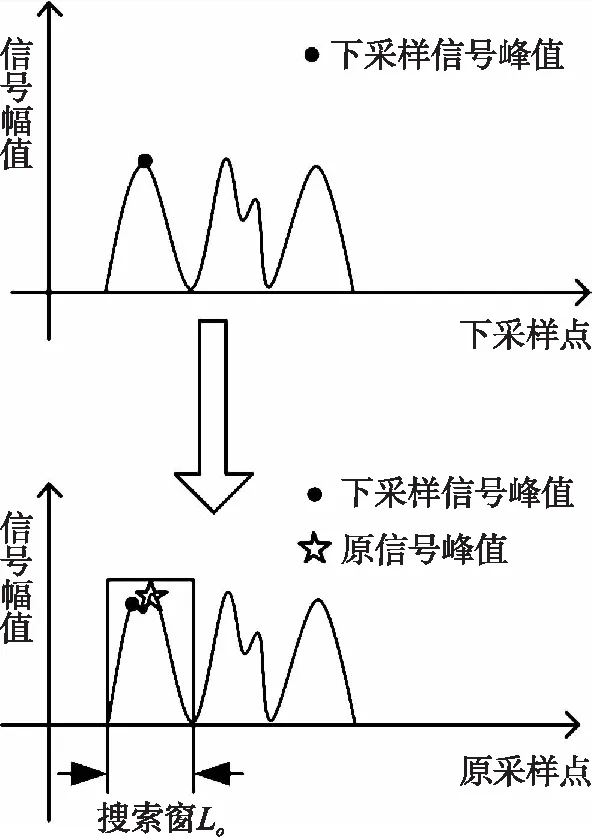
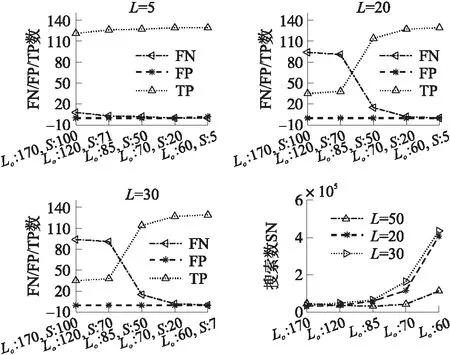
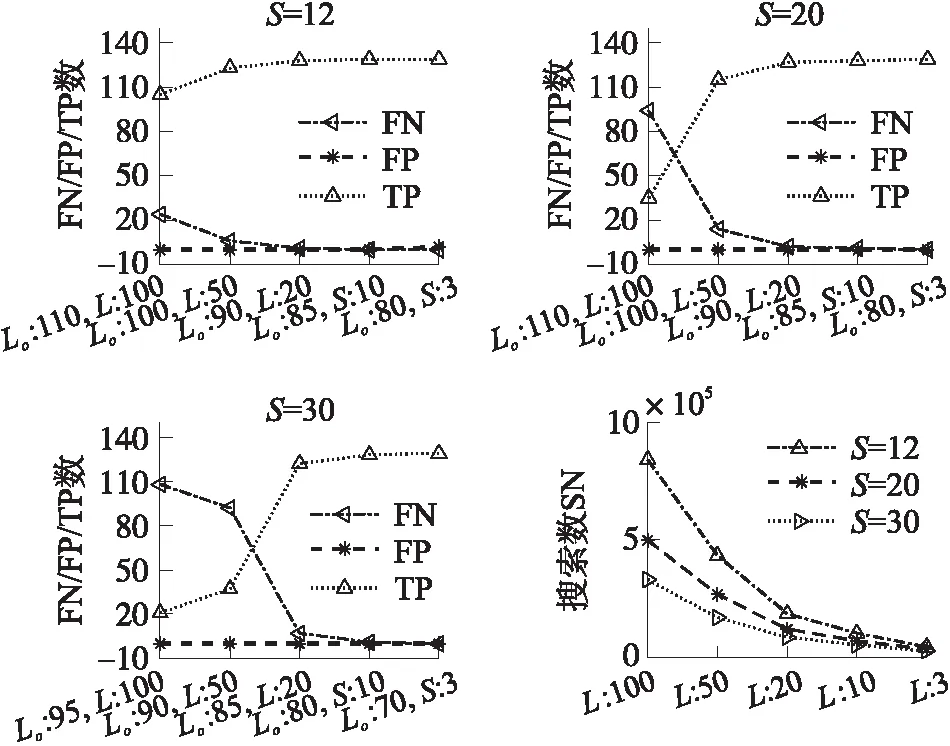
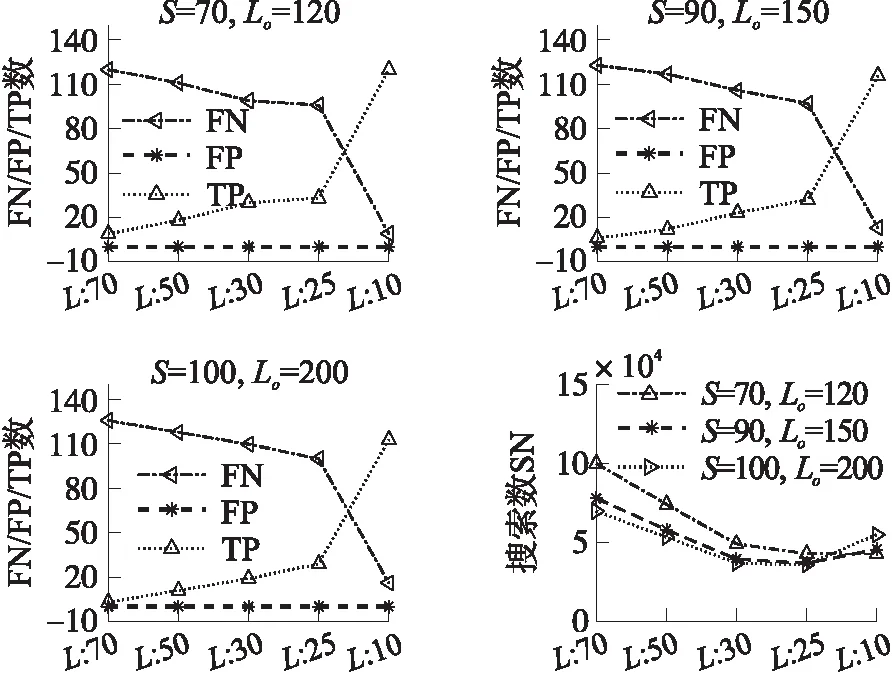
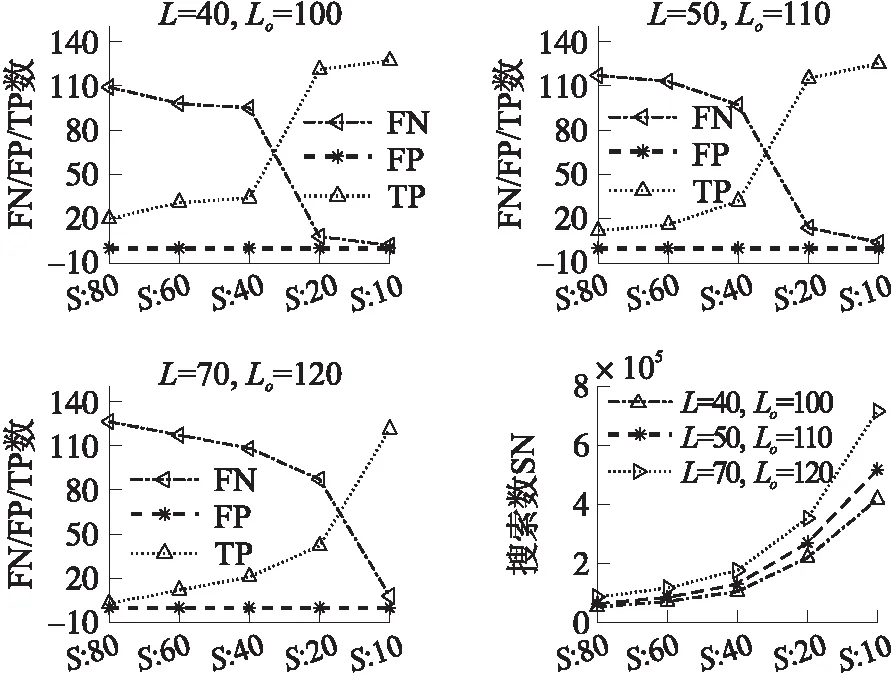
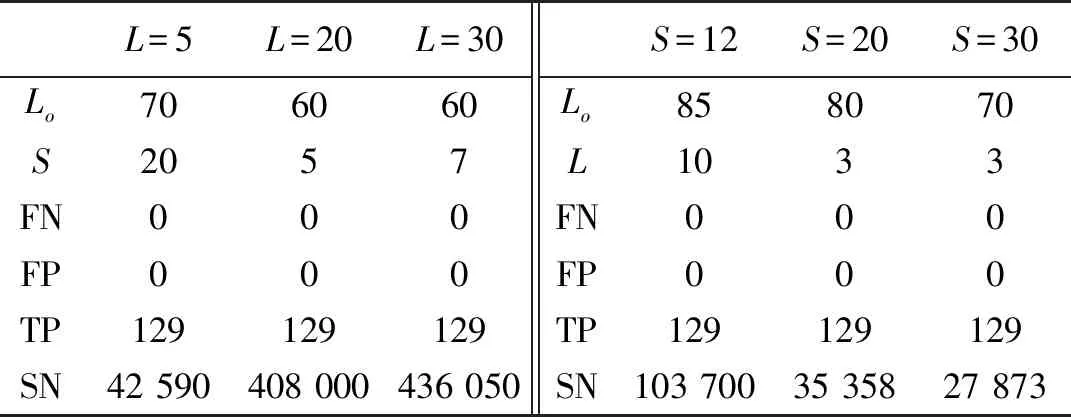
当xn 检测到道钉对应的峰值点,就需要将该峰值点的位置转化为道钉的公里标,从而确定道钉位置,完成定位。该定位过程包含以下两部分。 第一,将下采样点回溯至原采样点完成二次峰值搜索。假设经下采样平滑后信号的第n个采样点xn为一检测到的道钉峰值点,若满足 (8) 表1给出了当窗口滑动距离为1时,下采样二次搜索次数Nd×L+MpLo和非下采样搜索次数No×L′,其中L′和L分别是在原始信号检测峰值的窗口长度和下采样检测峰值的滑动窗口长度,Mp=|At|为检测的峰值点数。当采样倍数S较大时,由(1)可知Nd≪No。并且,若下采样和非下采样两者的窗口所覆盖的实际距离相等时,也有L≪L′。因此,忽略MpLo这一较小项,那么下采样的比较次数将远小于非下采样比较次数。 图5 下采样二次搜索示意图 搜索次数下采样二次搜索法Nd×L+MpLo非下采样搜索法No×L′ 第二,确定峰值点的公里标。由于磁力传感器信号以单位距离进行采样,因此峰值点公里标即是所求的道钉公里标。设磁力传感器信号以距离d进行采样,那么最终所求得的一道钉公里标为D=mod。 最后,给出道钉峰值检测步骤,如表2所示。 表2 道钉峰值检测算法 本实验中采集磁力信号的传感器利用图尔克传感器开发得到,传感器具体参数参见文献[9]。信号采集过程如图6所示,在一段弹条I型扣件的Ⅲ型混凝土轨枕(60 kg/m)的有砟铁路轨道上放置一辆有轮小车,该铁路具有完整的铁轨、枕木、道砟和道床,将磁力传感器固定于小车下方靠近铁轨处,使其能够感应到来自道钉或鱼尾板的磁力信号。然后,使小车匀速向前行驶,与此同时采集相应的磁力传感器信号。传感器采集的数据为一二维数据,一维为信号幅值,另一维为对应位置,即公里标。小车行驶距离约为100 m,按传感器1 mm距离采样,共采集到约98×103个数据点。对采集到的磁力传感器信号先经归一化至区间[0 1],然后再完成相应峰值检测。 图6 磁力传感器信号采集图 在本实验中,我们对比了多种算法的检测结果,分别是下采样滑动窗多峰检测算法(DSPD,Downsampling Slid-window Peak Detection)、非下采样滑动窗多峰检测算法(NSPD,Non-Downsampling Slid-window Peak Detection),以及自动多尺度峰值检测[10-11](Automatic Multiscale-based Peak Detection,AMPD)和斐波那契多峰检测[12](Fibonacci Peak Detection,FPD),其中DSPD和NSPD均为表2给出的道钉定位的峰值检测算法,两者区别仅在于是否使用了式(1)和式(8)的下采样二次峰值检测。另外,将式(7)的阈值分类法和PCA的K均值分类方法进行对比,K均值参数设置参见表3。以上算法的其他相关参数设置见表4。 表3 PCA和K均值参数设置 表4 各算法参数及初始化设置 图7 不同峰值检测算法的对比 最后,实验结果引入真阳性数(True Positive,TP)、假阴性数(False Negative,FN)即漏检数、假阳性数(False Positive,FP)和搜索次数(Search Numbers,SN)等指标来评判各算法性能。同时,还给出最大定位误差Emax的结果,定义为: (9) 2.2.1 峰值检测方案对比 图7给出DSPD、NSPD、FPD和AMPD四种峰值检测算法的FP,FN和TP数,其中DSPD和NSPD所选用的相关参数见表4。从图中可以看到,AMPD和FPD两种算法存在了漏检,而DSPD和NSPD在选用表4的参数时却不存在漏检和假阳。其原因在于AMPD和FPD的检测特性依赖于其参数选择,而参数的选择又由目标函数决定,由于道钉间距的随机性导致其磁力信号具有非平稳特性,因此选择固定的参数难以保证AMPD和FPD能够找到所有峰值点。 2.2.2 峰值分类方案对比 图8给出了阈值法和K均值对道钉和鱼尾板峰值信号的分类结果,图9还给出了K均值分类中聚类的结果图。从图8可以看到,K均值法存在了一定的FN数,因此其TP数也没有达到期望值。另外,K均值需先完成PCA降维才能完成无监督聚类(聚类过程见图9),因此其复杂度也比阈值法要高。相反,阈值法分类的FN和FP数均为0,取得了较好的分类结果。 图8 不同峰值分类方法结果 图9 峰信号波形及聚类图 图10 NSPD和DSPD检测对比结果 2.2.3 下采样和非下采样方案对比 图10(a)和10(b)分别给出了NSPD和DSPD两种方案的对比结果。从图10可以看出,两种方案在选用合适的参数时,均能使FN和FP数降为0,例如NSPD在L′=58和DSPD在Lo=70,S=20时。然而,两者的搜索次数却有较大差别,前者的搜索次数达到了106~107的量级,而后者的次数仅有104的量级。这一结果也表明,即使两种算法均能保证不出现假阳和漏检,但是NSPD的搜索次数要多于DSPD,因此,采用下采样方案能够减少算法的搜索次数。 2.2.4 参数L、Lo和S对算法的影响 在本小节中,将给出搜索窗口长度L、二次搜索窗口长度Lo和下采样频率S对DSPD算法性能的影响。首先,图11给出了DSPD在L=5,20和30下,检测结果随Lo和S的变化曲线图。从图11中可以看到,较小的L不仅有较小的搜索次数,而且也不会出现漏检。因此,选用较小的L既可以保证较好的峰值检测性能,同时也有较小的搜索次数。但是,也应注意到,当L=5和S=5时,出现了假阳。这一结果表明,在选用较小L时,应保证较大的S,以避免出现假阳。 图11 固定L变Lo和S峰值检测结果(DSPD) 图12 固定S变Lo和L峰值检测结果(DSPD) 图12给出了DSPD在S=12,20和30下,检测结果随Lo和L的变化曲线图。从图中可以看到,选择大的S可以有较少的搜索次数,同时为了保证不出现漏检,还需要选择较小的L。图13还给出了DSPD在固定Lo和S的情况下,检测结果随L的变化曲线。从该图中也可以看到,较小的L能保证较少的搜索次数和较少的漏检数,这一结果也与图11和图12一致。另外,图13还显示了,较大的Lo也会使漏检数增大。 图13 固定S和Lo变L峰值检测结果(DSPD) 此外,图14给出了DSPD在固定Lo和L的情况下,检测结果随S的变化曲线。从图中可以看到,一方面S增大会减少搜索次数,但另一方面也会增大漏检数。另外,与图13一致的是,应取较小的Lo,此时既能减少搜索次数,也能减少漏检数。 图14 固定L和Lo变S峰值检测结果(DSPD) 最后,由图11~图14的结果可知,若使DSPD的假阳和漏检均为0,L,Lo和S的参数组合其实并不唯一。为寻找较优参数组合,表5给出了DSPD在FP和FN均为0时,几组L,Lo和S的参数值。从表5可知,最后一列的参数组合不仅能得到0漏检和0假阳,且搜素次数也仅为104量级。该结果也表明了,DSPD的参数选用应该采用较小的L和较大的S和适中的Lo。 表5 DSPD最优检测下不同参数组合情况 2.2.5 最大道钉定位误差 在本节最后,给出本文算法的最大道钉定位误差,其定义参见式(9),结果参见表6,其中的参数选择是保证最后的峰值检测漏检和假阳数为0。从表中结果看,算法的定位误差没有超过1cm,其误差来源主要在于,一个道钉会对应于多个传感信号的峰值,或者该峰值在更小的刻度下会退化为一条直线,如图4所示。但是,本实验的测试轨道枕木间距离通常为570 mm~625 mm(以每公里铺设轨枕数目而定)。 表6 DSPD最大定位误差 通过有砟铁轨上所得到的磁力传感信号,本文研究了一种可定位道钉的峰值检测算法,主要通过与传统方案的对比确定一种简单易行的检测方案,并通过对算法相关参数分析和测试来确定较优的参数选择。虽然在实验中,我们对算法的方案和各参数进行了详细的对比,并给出了一些实验结果,但是还有以下一些问题需进一步讨论。 首先是鱼尾板峰值检测问题。由磁力传感器信号可知,当出现鱼尾板时,道钉的峰值信号将被淹没于其中,因此难以被检测到。本文仅讨论了如何区分鱼尾板和道钉的峰值信号,并没有讨论如何在这种情况下进行检测。正如前文所述,本系统将是一个联合定位系统,当磁力传感信号无法定位道钉时,将由图像检测的方法去弥补。由于图像检测方案将涉及到另外的算法,本文将不再过多介绍。 其次是定位误差问题。实验中给出的定位误差是算法检测到的峰值点与磁力信号上实际峰值点间的距离,而真正的定位误差应是算法检测的峰值点与实际道钉位置间的距离,但是后者的误差不仅取决于峰值检测算法的性能,还取决于磁力传感器本身特性。若磁力传感器信号峰值点与道钉位置产生偏差,那么即使算法再精确也难以定位准确。因此从该角度看,使用精确的磁力传感器也是决定道钉定位准确性的一个因素。另外,对道钉的定位来确定下镐位置本身具有局限性,因为道钉的安装位置会变化,因此确定轨枕间的距离就会发生偏差。为了确定道钉误差是否会导致下镐定位错误,我们对实验中弹条式扣件的安装位置进行了测量。Ⅲ型混凝土轨枕的宽度为320 mm,道钉距离铁轨中心线的长度变化范围为3 mm~4 mm,相邻轨枕中心点间的距离与每公里铺设轨枕数目有关,实际测量值范围为570 mm~625 mm(理论值为543 mm~625 mm)。通常,下镐空间是由相邻轨枕间距减去轨枕宽度、下镐保护间距和单个镐头的顶端宽度得到,实验中我们得到的下镐空间实际值为140 mm~195 mm,其中所使用的单个镐头的顶端宽度为10 mm,保护间距为100 mm(离上轨枕和下轨枕边沿各50 mm)。因此由以上数据可得,扣件安装位置是否会带来定位误差主要取决于扣件是否真正安装在轨枕宽度方向的中心线上。若安装在中心线上,则道钉间距就等于相邻轨枕间距。对于我们所实验的铁轨,道钉确实安装在轨枕宽度方向的中心线上,距离轨枕两边沿距离相等。因此,若对于Ⅲ型混凝土轨枕的弹条式扣件轨道,其安装按标准执行,那么可保证道钉间距将可认可为轨枕间距。 第三是滑动窗口距离问题。从搜索的角度看增大距离可以减少滑动窗口数,因此也能减少搜索次数。但反过来,增大滑动距离又会导致漏检。在实验中,我们仅仅考虑了滑动窗口距离为1的情形,其原因在于,提高下采样频率实际等效于增大滑动窗口距离,因此并未过多考虑其他滑动距离的情形。 图15 多道钉和组金属扣件系统图 第四,本文算法主要针对弹条式扣件的铁轨,在该扣件系统中,只有单个道钉或螺栓。在实际工程应用中,存在多个道钉或一组金属组件的轨道情形,如图15所示,此时得到传感信号会产生变化,从而带来检测误差。针对该情况,仍然可采用联合传感器检测方法,先通过分类方法,区别单道钉的信号和组金属件的信号,若是后者,则用图像检测的方法确定下镐位置。 最后是关于漏检问题。若漏检并不是一个特别需要考虑的因素,例如我们可用图像检测方式去弥补漏检的道钉时,那么我们可以通过牺牲漏检来换取算法的其他性能。从实验结果看,下采样频率增大可以有效减少搜索次数,那么大采样频率虽然会产生一些漏检数,但是却得到更快速的峰值检测算法。 本文提出了一种可根据磁力传感信号定位道钉的峰值检测算法,在该算法中我们对比了多种检测方案,并对算法的相关参数进行了分析。 实验中,采用了一组在弹条I扣件Ⅲ型混凝土枕60 kg/m有砟铁轨上得到的磁力传感信号对算法进行测试,实验结果表明,采用下采样、滑动窗口峰值检测、阈值分类和二次峰值检测的方案具有较优的检测性能。同时,为了保证算法不出现假阳和漏检,并减少计算复杂度,算法还应考虑较小的窗口长度,较大的下采样频率和适中的二次搜索窗口长度。 最终,当窗口长度设置为3,下采样频率设置为30和二次搜索窗口长度设置为70时,漏检和假阳均为0,搜索次数仅为104量级,而最大道钉定位误差未超过1 cm。1.5 二次峰值检测



2 实验
2.1 实验设置

2.2 实验结果及分析







3 讨论

4 结语
