贸易模型发展综述:共性和异性视角
2019-11-27佟家栋
王 芊,佟家栋
(南开大学 经济学院,天津 300071)
一、研究对象
国际贸易相关问题的研究是经济学一个古老而重要的组成部分,由古典经济学开始,国际贸易问题就是经济学研究的重点之一。由古典经济学集大成者大卫·李嘉图提出的比较优势理论,至今仍然是贸易理论的重要基石。自以萨缪尔森(Samuelson)为首的经济学家开创了经济分析的范式,将数理模型作为经济理论的正式表述方式开始,贸易理论模型基本经历了新古典贸易理论(neoclassical trade theory)—新贸易理论—新-新贸易理论的发展阶段。本文旨在沿着贸易理论发展历史的脉络,从其共性和异性的角度出发,通过对经典文献的梳理,对代表性的贸易理论模型进行综述。
本质上,贸易理论模型是对一般均衡理论的应用,无论何种模型,都遵循一些共同的设定。区别于一般均衡理论,在贸易模型中,市场被严格区分为“商品市场”和“要素市场”。商品可以在国际间自由流动,存在一个统一的“国际市场”和“世界价格”;而要素则不可在国际间流动,只存在“国内市场”。国际贸易理论只关注商品的贸易,而排除了要素的流动。贸易理论的核心是解释商品市场的国际化如何影响商品价格,商品价格变化又如何反过来影响国内要素市场价格、要素资源配置、生产和福利等。贸易模型主要刻画供给侧,对于需求侧则保持了相当简单的一般性假定,即典型贸易理论并不认为国别间消费者偏好的差异是贸易的驱动力。因此,对于不同贸易模型的区分标准是其供给侧的设定。
广义的新古典贸易理论是指从19世纪30年代至20世纪80年代占据国际贸易学主流位置的贸易理论,其核心是比较优势原理,即国别间商品相对价格的差异。新古典贸易理论继承了古典经济学的观点——完全竞争、规模收益不变和市场出清,将其作为分析的起点。按照比较优势来源的不同,新古典贸易模型可区分为李嘉图模型(Ricardian model)和要素比例模型(H-O模型)。李嘉图模型认为国别间生产率的差异是比较优势的来源;而要素比例模型则认为国别间要素禀赋的差异是比较优势的来源。需要说明的是,新古典贸易理论的核心思想早在经济分析方法完善之前就已出现,但模型化则是在20世纪中后期才完成。本文所述的“新古典贸易模型”特指数理模型化的新古典贸易理论。事实上,新古典贸易模型具有旺盛的生命力,并未因为新贸易理论乃至新-新贸易理论的出现而失色。实际上,目前两种最主流的贸易模型之一的伊顿-科图姆(Eaton-Kortum,EK)模型[1],其实质就是刻画了企业异质性的李嘉图模型。
克鲁格曼(Krugman)模型是新贸易理论的核心,其出现背景是传统模型在解释工业化国家之间的贸易和产业内贸易的乏力。克鲁格曼(Krugman,1979、1980)大胆放弃了完全竞争和规模报酬不变(constant return to scale,CRS)(1)CRS是古典经济学的一个核心观点。可以证明,如果所有投入物,包括企业家才能等“隐藏要素”都可以明确界定,那么复制生产总是可行的[2]。按此观点,规模报酬递减(decreasing return to scale,DRS)必定反映了某种潜在要素的稀缺性。因此,通过引进无弹性供给的隐藏要素,DRS可以和新古典贸易模型相容。规模报酬递增(increasing return to scale,IRS)是个更为复杂的情况,并且也是新贸易理论的基石,后文会再对此进行探讨。的新古典假设,从而从与新古典模型完全不同的角度解释了贸易的产生和利得[3-4]。即使在消费者偏好、技术和资源禀赋完全相同的条件下,规模报酬递增(increased return to scale,IRS)的技术也会促使贸易发生并使贸易参与国获得贸易收益。梅里兹(Melitz,2003)[5]在克鲁格曼模型的基础上,发展了具有企业异质性的垄断竞争贸易模型,从而开创了新-新贸易理论。
本文将EK模型和梅里兹模型放在一起介绍,虽然它们在基本假设上具有本质的区别,但其对贸易理论发展的贡献都是通过将企业生产率内生化实现的。可以简单地认为,EK模型是具有企业异质性的新古典贸易模型,梅里兹模型则是具有企业异质性的克鲁格曼模型。
为贸易引力方程(gravity equation,GE)提供结构性基础,是贸易理论发展的另外一支脉络。可喜的是,EK模型和梅里兹模型(包括扩展的克鲁格曼模型)都可以导出贸易引力方程,从而将数理模型同贸易数据直接联系起来。贸易引力方程在经验研究上的成功,反过来印证了贸易模型的可信性,并赋予了模型定量的含义。尽管对贸易利得来源的解释不同,定量贸易模型在回答贸易利得究竟是多大这个问题上却给出了一致的答案6]。在福利分析的层面上,具有不同性质的贸易模型被统一起来,是近年来贸易理论领域最重要的成果。
二、新古典贸易模型
本文所讨论的新古典贸易模型(neoclassical trade models)意指承袭古典政治经济学思想,使用标准经济分析的建模方法,研究贸易的形成、特征和影响的经济学模型。
(一)新古典模型的共同假设和一般结论
新古典贸易模型之所以继承了古典政治经济学的精神,是由于其都遵守以下三个假定:完全竞争市场,生产技术具有规模报酬不变的性质,以及不存在任何形式的价格扭曲。
在新古典贸易理论框架下,根据以上三个共同假设,在不考虑模型具体设置的情况下,仅根据一般均衡理论,就可以得到两个重要的一般性结论。第一个结论是关于贸易利得(gains from trade,GT),第二个结论是关于比较优势(comparative advantage,CA)。
萨缪尔森(Samuelson,1939)[7]用对偶理论(2)迪克西特和诺曼(Dixit & Norman,1980)[8]系统介绍了使用对偶理论研究国际贸易问题的方法,对偶理论是新古典贸易理论中常用的标准数学工具之一。证明了,在新古典模型框架下,贸易会使所有国家都受益。定理如下:
定理(贸易获利):在各国均只存在一个代表性家庭的新古典贸易模型中,自由贸易会使所有的贸易参与国受益。
贸易获利定理的实质是贸易使生产可能性边界发生了扩张。迪克西特和诺曼(Dixit & Norman,1986)指出,即使不存在代表性家庭,如果政策工具可以充分发挥作用,例如转移支付、税收和津贴等,自由贸易仍可使所有国家都获得帕累托(Pareto)改进[9]。
新古典贸易理论的第二个结论就是广为人知的比较优势定理(Law of Comparative Advantage)。如果说贸易利得定理是新古典贸易理论最重要的规范性结论,那么比较优势定理则是最重要的实证性结论,它指明了贸易的原因和特征。比较优势定理指出,封闭经济下价格的相对差异是贸易之所以产生的根本原因。在两商品模型中,每个国家都会选择出口其封闭经济价格相对低,也就是其具有比较优势的商品;而选择进口其不具有比较优势的商品。
多产品情形下的比较优势定理的正式表述和证明,是由迪尔多夫(Deardoff,1980)[10]给出的。用t≡(y1-c1,…,yG-cG)表示某国的净出口,pa表示其封闭经济价格,p表示世界价格,其他符号的意义与之前相同,可以得到如下定理:
定理(一般情形下的比较优势):在新古典贸易模型中,如果某国存在一个代表性家庭,则有cor(p-pa,t)≥0。
迪尔多夫的比较优势定理表明,在多产品情形下,商品是否具有比较优势同其是否出口只具有相关关系。比较优势定理仅是一个新古典贸易理论框架下的一般结论,并未解释为何会产生pa的相对差异。对pa的差异来源的不同解释,使得新古典贸易模型进一步被区分为李嘉图(Ricardian)模型和要素比例模型。
(二)李嘉图模型
大卫·李嘉图作为英国古典政治经济学的集大成者,其很多经济学思想对现代经济理论仍有重要影响。李嘉图认为,国家间的技术差异是比较优势之所以形成的原因,并导致了国际贸易。李嘉图思想现代经济模型化的经典表述是多恩布施等(Dornbusch et al.,1977)[11]刻画的DFS模型,被认为是“标准李嘉图贸易模型”。
由于李嘉图认为技术差异是比较优势的根源,所以几乎所有形式的李嘉图模型都假定只存在一种生产要素——劳动,也可将这种生产要素理解为所有生产要素(当然是不可贸易的)加总而成的复合生产要素。这种理解的前提是,国别间的要素强度不应存在系统性差别。
假定一个两国经济——本国和外国,外国的相关变量以星号表示。L和L*分别表示两国的劳动要素禀赋,w和w*分别表示两国工资水平。假定商品空间是个连续统[0,1],商品z∈[0,1]:

在需求侧,按照新古典贸易模型的惯例,假定整个世界具有相同的位似偏好,则对商品z的支出占总支出的份额b(z)∈(0,1)满足:
(1)

DFS模型的第一个自由贸易均衡条件刻画了贸易导致了有效的国际分工。根据利润最大化条件:
p(z)-wa(z)≤0,如果z在本国生产则取等号
(2)
p(z)-w*a*(z)≤0,如果z在外国生产则取等号
(3)
可以很容易证明以下定理:


(4)
ω表示(本国的)相对工资。

(5)
即:
(6)
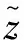

图1 DFS模型的均衡
根据萨缪尔森贸易获利定理,所有新古典贸易模型中都存在普遍的贸易获利。在DFS模型中,贸易利得非常明显,即在开展贸易后,所有商品的价格都不会上升,所以代表性家庭的福利一定会提高。
DFS模型具有良好的比较静态性质,可以简单直观地分析诸如相对人口增长,技术进步等情形的比较静态含义。但其也有一个相当明显的缺陷,即很难在保持原有结构的情况下扩展为一个多国模型。在DFS模型中,每一国都会专门化生产相对另一国具有比较优势的商品。当试图将模型扩展到多国时,无法确定本国将应该和哪一国或哪些国家去比较,也就是说,无法确定“另一国”是谁。有相当多的研究对李嘉图模型如何扩展到多国情形做出了探索,例如,琼斯(Jones,1961)将研究限定在每个国家只生产一种商品的情形上[12];科斯蒂诺特(Costinot,2009)通过对不同产品的单位劳动需求施加了结构性限制而将李嘉图模型扩展到多国[13]。在对李嘉图模型的发展中,最成功、影响最大的是伊顿和科图姆(Eaton & Kortum,2002)[1]。EK模型不仅是目前李嘉图模型最现代化的版本,并且直接推动了梅里兹模型的出现,本文的第三部分将会介绍EK模型。
(三)要素比例模型
广义的要素比例模型(factor proportion theory)包括李嘉图-瓦伊纳(Ricardo-Viner,RV)模型[8,14]和赫克歇尔-奥琳(Heckscher-Ohlin)模型,狭义的要素比例模型一般仅指H-O模型[15],从长期均衡的角度看,H-O模型可以替代RV模型。要素比例理论的特征是认为要素禀赋的差异是比较优势的源泉,其一般结构是假定国家间在要素丰裕性上存在差异,也就是存在相对要素供给上的差异;同时产品间在要素需求强度上有差异,也就是相对要素需求上的差异。相对要素供给和需求决定了国别间封闭经济状态时相对价格的差异,从而决定了贸易的特征。
H-O模型是跟“维度”非常相关的一种新古典贸易模型。所谓的“维度性”是指模型所假定的商品数量和要素数量的相对关系,经典的H-O模型是2×2的,即假定存在两种商品、两种要素。在小型开放经济设定下,世界价格是外生变量,因此没有必要考虑商品市场出清。小型开放经济情形的2×2H-O模型的第一个经典结论是要素价格均等化定理,即如果两个国家之间进行自由贸易,且不存在技术差异,在均衡下都同时生产两种产品,那么每个国家的要素价格完全由商品价格决定,也即具有同样的要素价格。要素价格均等化定理的含义是,虽然要素被认为是不可贸易的,但商品贸易可以“完美的替代”要素贸易。尽管国家之间有着不同的要素禀赋,自由贸易会促使资源在部门间重新分配从而使各国保持同样的要素价格。
小型开放经济的第二个经典结论是施托尔帕-萨缪尔森(Stolper-Samuelson,S-S)定理。根据S-S定理,一种商品价格的上升会导致这种商品相对使用强度大的那种要素的实际价格上升,另一种要素的实际价格下降。
如果放弃小型开放经济的假定,转而研究两国经济(北方国家和南方国家),即2×2×2的H-O模型,那么世界价格将不再是外生的。具体来说,存在两种商品,g=1,2;两种要素,f=l,k;两个国家,c=n,s。令af,g(w,r)表示商品g对要素f的单位需求,假定:
(7)

2×2×2的H-O模型核心结论是每个国家都会出口对其相对充足要素的相对使用强度大的商品,即北方国家出口商品2,进口商品1;南方国家反之。这就是H-O定理所表达的意思。
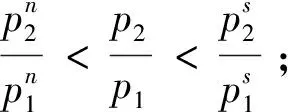
前文已经提到,H-O模型高度依赖其“维度”的设定。经典的2×2模型可以比较顺利推广到n×n的情形中;但当假定商品数量大于要素数量,或者要素数量大于商品数量时,结果就会出现较大的变化。高维H-O理论最重要的结论是赫克歇尔-奥琳-瓦涅克(Heckscher-Ohlin-Vanek,HOV)定理。HOV定理的含义是,从生产商品所用要素的角度来看,每个国家最终实际都在出口其相对充足(相较于世界的要素禀赋)的要素。关于高维的要素比例模型,可以参考埃蒂尔(Ethier,1984)[16-17]的论述。
在贸易理论发展的历史上,要素比例模型曾经占有相当重要的地位;但从现代贸易模型的角度来看,单纯的要素比例模型已很难再占有一席之地,其生命力远远不及同为新古典模型但出现的更早的李嘉图模型。H-O模型关于贸易对收入的影响的预测和现实中观察到的情况并不相符。在现实世界中,更多的是发展中国家走向贸易开放后,虽然其整体收入水平常常经历显著增长,但同时收入不平均也随之增加,这和H-O模型的预测是矛盾的。并且,H-O模型对于解释工业化国家之间的贸易和中间品贸易也比较乏力。尽管其对贸易特征和影响的解释不及更现代的贸易模型,但H-O模型的核心思想——部门间对要素需求的差异会在一定程度上影响贸易的结构,贸易也会反作用于部门间的资源配置,仍然在很多现代贸易模型中得到继承。
三、克鲁格曼模型
(一)克鲁格曼模型简述
克鲁格曼模型是新贸易理论的核心,由克鲁格曼于1979年和1980年的经典论文中提出。新贸易理论同新古典贸易理论在出发点上具有根本性的不同,它放弃了新古典模型的两个核心假设:完全竞争市场和规模报酬不变,从而从与新古典模型完全不同的角度解释贸易的产生和利得。
克鲁格曼模型产生的背景是战后全球化的大发展,工业化国家之间的和产业内的贸易规模越来越大,这是经典新古典贸易模型,也就是比较优势理论无法解释的。在此种背景下,新的贸易理论呼之欲出。迪克西特和施蒂格林茨(Dixit & Stiglitz,1977)[18]关于垄断竞争和产品多样性的经典文献,为克鲁格曼模型的产生奠定了理论基础。不同于新古典模型,克鲁格曼认为相对成本(同时也就是相对价格)的差异不是贸易产生的必要条件,即使在消费者偏好、技术和资源禀赋完全相同的条件下,规模经济也会促使贸易发生并使贸易参与国获得贸易收益。
在1979年和1980年发表的两篇论文中,克鲁格曼重复论述了其新贸易模型,1980年版可视作1979年版的修订版。鉴于1979年版模型较为简洁,并且已经可以完全体现克鲁格曼模型的全部思想,本文在此主要介绍这个模型。
在需求侧,假定整个世界具有相同的效用函数:

(8)

在供给侧,假定某国的劳动力禀赋为(人口)为L,生产技术具有IRS的性质,对品种i的商品的劳动要素需求是:
(9)
其中,f是固定成本(以劳动力度量),固定成本的存在是生产技术呈现规模报酬递增的原因;qi是i的产量;φ是常数,也可以理解为代表生产率的参数,克鲁格曼模型没有包括企业异质性,因此φ对所有商品是相同的。
由消费者效用最大化可得:
pi=λ-1u′(ci)
(10)

克鲁格曼设定了垄断竞争的市场结构,生产企业具有定价权,根据垄断定价:
(11)
垄断竞争市场具有自由进入的性质,潜在生产企业会进入市场直至所有企业的超额利润降为0,所以:
(12)
企业所获得的利润刚好可以弥补固定成本。
根据商品市场和要素市场的出清:
(13)
为了突出规模经济的作用,克鲁格曼(Krugman,1979)假设了完全对称性[2],因此,∀i,pi=p,qi=q,ci=c。
由式(11)、式(12),可以得到克鲁格曼模型的两个封闭经济均衡条件:
(PP)
(ZP)

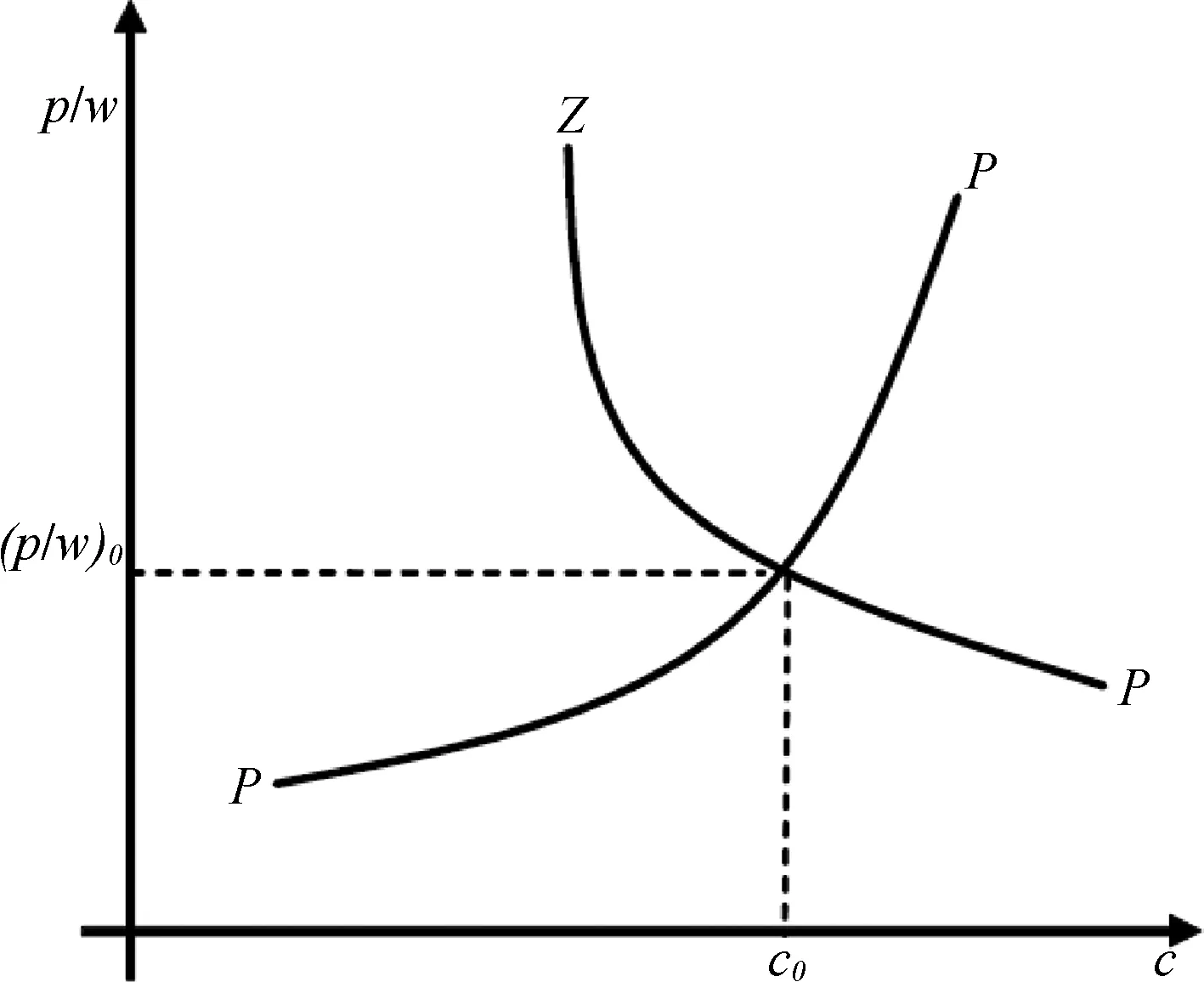
图2 克鲁格曼模型的均衡
现在假定世界由两个完全对称的国家组成,按照新古典贸易模型,贸易的动机必定是参与国在不同的商品上具有相对成本优势,因此完全相同的国家间没有产生贸易的可能性。然而,克鲁格曼模型指出,即使在这种完全对称的情形中,开放贸易也会使参与国获得收益。在克鲁格曼模型中,贸易开放等价于参与国人口发生增长,(ZP)曲线向左下方移动;(PP)曲线不受影响。其结果是对某特定品种商品的消费降低(c1 (14) 实际工资上升使得产量增大,市场均衡向完全竞争方向移动,这就是贸易导致的“竞争促进”效果。 根据市场出清条件,可得市场中存在的商品品种数目为: (15) 尽管在这个原始版本(1979)的模型中,克鲁格曼阐明了如果市场具有垄断竞争的结构,那么即使在消费者口味、技术、资源禀赋完全相同的条件下,规模报酬递增的技术也会促使贸易开放并使贸易的参与国获得利益,但该模型并未指出贸易的方向[3]。在1980年的论文中,克鲁格曼进一步指出,一个国家将倾向出口其具有较大的国内市场的商品,并称其为“母国市场”效应(home market effects)[4]。 客观地说,从现在的观点来看,克鲁格曼模型的设定并不非常精细,其本质是不具有企业异质性的垄断竞争模型。在下一部分中本文要探讨的具有企业异质性的垄断竞争模型,亦即梅里兹模型,可以视作克鲁格曼模型的完善版本。由梅里兹模型可以得到几乎所有克鲁格曼模型的结论。尽管如此,克鲁格曼模型仍被认为是国际贸易理论领域开创性的成果,对其之后的研究产生了深远影响。并且克鲁格曼模型具有令人叹服的简洁性,相比于之后出现的各种复杂模型,它用相当简约的结构阐述了深刻的洞见。 在1979年的论文中,克鲁格曼假定了一般形式的效用函数[3];而在1980年的论文中,他采用了封闭形式的效用函数[4],也就是具有不变价格替代弹性的CES效用函数,更确切地说,是迪克西特-施蒂格林茨(Dixit-Stiglitz)偏好(4)在克鲁格曼之前的贸易理论文献中,对偏好常见的假定是位似性,或者显性的使用科布-道格拉斯(Cobb-Douglas)效用函数。可以证明C-D函数是CES函数在σ→1时的极限形式。。从克鲁格曼开始,CES函数成为了贸易理论中最受欢迎和最常用的需求侧设定。CES函数有多种形式,最常用的是勒贝格(Lebesgue)积分形式: (16) CES函数具有位似性,如果采用具有外指数的形式,即: (17) 则它不仅是位似函数,还是一次齐次函数。由于位似性,代表性消费者在某种特定商品上的支出占总支出的比例同收入无关,这使得模型结构大大简化,并且可以很方便地推导价格指数,从而进行福利分析。几乎所有能导出结构化引力方程的模型,在需求侧都使用了CES偏好的假定,如阿科拉克斯等(Arkolakis et al.,2012)[6]。这些引力方程在经验研究中的成功也证明了CES偏好的合理性。 数据可得性的扩展和计算能力的提高,促成了20世纪90年代国际贸易研究领域经验研究的爆发,大量的经验研究[20-21]将分析推进到企业层面。然而在贸易理论层面,还没有一种模型能够刻画企业层面的异质性。 进入到21世纪,这种情况得到了根本性的改变。伊顿和科图姆(2002)[1]、梅里兹(2003)[5]的两篇经典论文成功地建立了具有内生企业生产率的贸易模型,从而开创了贸易理论的新时代。从性质上来说,EK模型的起点是DFS模型,具有新古典性质,它的出现被认为是李嘉图模型的复兴;梅里兹模型的理论起点是克鲁格曼模型,它舍弃了完全竞争和CRS的经典假设,因而被称为“新-新贸易理论”。 EK模型保留了新古典经典假设,即完全竞争、规模报酬不变的技术和市场出清。在需求侧,同DFS一样,EK模型假设商品空间是连续统[0,1]。但不同于DFS模型,EK模型刻画了多国情形,世界由i=1,…,N个国家组成。各国的代表性消费者具有同样的CES偏好: (18) 在供给侧,和传统李嘉图模型一致,只有一种生产要素——劳动。生产技术具有CRS性质,i国单位生产要素的价格为ci,在不考虑中间投入品的情况下,ci等于i国的工资水平wi。 EK模型的关键假定是,所有生产企业的生产率,都独立同分布的服从于费雷谢(Fréchet)分布。令zi(ω)为i国所有生产ω商品的企业的生产率,由独立同分布假定,可以省略品种变量ω,有: Pr(zi≤z)=Fi(z)=e-Tiz-θ,θ>1 (19) 如果i国企业要将商品出口到n国,它还面临冰山成本dni≥1,即它若出口一单位商品,需运送dni单位商品。 分布参数Ti是特定于国别的,它刻画了技术的绝对优势,Ti越大,则i国生产任何商品的生产率都越高。参数θ对i=1,…,N均相同,它刻画了分布的集中趋势,θ越大,分布越集中。在贸易中,越分散的生产率分布越有可能使比较优势发挥作用。关于费雷谢分布合理性的分析,可参考伊顿和科图姆(Eaton & Kortum,1999)[22]。 接下来介绍EK模型的几个关键结论。 1.价格分布 (20) 对于n国来说,它将选择价格最低的供应国,Pn=min{Pn1,…,PnN}。因此,某种商品在n国的价格分布Gn(p)=Pr(Pn≤p)为: Gn(p)=1-∏iPr(Pni≥p)=1-∏i[1-Gni(p)]=1-e-Φnpθ (21) Φn对于EK模型是个非常重要的参数,刻画了世界的技术水平、要素成本以及n国所面临的地理壁垒。通过利用其他国家的技术,贸易扩展了一个国家的实际技术水平;这种正向作用又会受到要素成本和贸易壁垒的抵消。可以通过考虑两种极端情况了解Φn的意义。第一,可以考虑所谓“零重力”,也就是不存在贸易壁垒的情形。此时,∀i,dni=1,因此Φn对所有n均是相同的,一价定律将成立。第二,考虑dni→,∀n≠i,即阻止性贸易壁垒的情况,那么将会回到自给自足的状态,价格分布仅由n国自己的技术水平和要素成本决定。 2.购买的分布 对于某特定的商品,n国一定会从提供最低价格的国家购买,即argmin{Pn1,…,PnN},所以,从i国购买的概率是: (22) 此概率等于i国对参数Φn的贡献率。 3.条件价格分布 假定对于某商品,i国向n国提供的价格为q,并且其他国提供的价格均高于q,发生此种情况的概率是: (23) (24) 由于πni是i国向n国出口的概率,所以i国是n国实际供给者为条件的概率分布是Gn(p)。可以发现,这和无条件价格分布是相同的。这说明,在EK模型中,所有的调整都发生在广延边际上,更偏远、要素成本更高或具有较低Ti的国家提供较少的商品种类,但是平均价格与谁是出口者无关。 4.价格指数 (25) 有了之前的结论,可以继续推导EK模型的均衡条件。由条件价格分布等于无条件价格分布的性质,平均价格同出口国i是谁无关,再由大数定律,n国对i国商品的支出比例等于对i国某特定商品的购买概率πni。用Xn表示n国的总支出,用Xni表示n国在i国商品上的支出,则有: (26) 式(26)即EK模型的均衡条件。和传统贸易模型不同,EK模型并未对出口种类做出预测,而是刻画了贸易流量,因此它可以直接用于经验研究。为了更清楚地看到这点,可以根据式(26)推导引力方程。令Yi=∑nXni表示i国的总产出,则: (27) Xni=γ-θXnYidni-θ(pnΩi)θ (GE) 这就是引力方程。其中,dni表示双边阻力,pn和Ωi分别表示内向的和外向的多边阻力。 由于EK模型对引力方程做出了结构化的解释,它可以直接同贸易数据相结合,定量估计GT。具有此类特点的模型被称为量化贸易模型(quantitative trade model),在本文第五部分会对这个领域进行介绍。 梅里兹模型设定了和克鲁格曼模型相同的基本假定:垄断竞争和IRS。在需求侧,代表性消费者具有CES偏好,对商品ω∈Ω的需求函数和支出分别是: (28) (29) 在供给侧,同克鲁格曼模型一致,梅里兹假定劳动是唯一的生产要素,其禀赋为L,工资水平w≡1,生产技术具有规模报酬递增的性质,则有: (30) 其中,φ表示企业的生产率。 由垄断定价规则,具有生产率φ的企业将会定价: (31) r(φ)=R(Pρφ)σ-1 (32) (33) 根据以上基本设定,可以得到: (34) 即生产率更高的企业生产更多的产量,并获取更高的收入,这和经验证据是相符的。 1.封闭经济 令M为均衡中实际生产的企业(存活企业)的测度,μ(φ)为存活企业生产率的概率密度函数(5)μ(φ)实际上是条件概率密度,这点在下文的推导中可以看到。,则: (35) 利用定价式(31),可得: (36) 由于梅里兹模型设定了垄断竞争的市场结构,因此必须确切定义企业的进入和退出,梅里兹参考了霍彭哈恩(Hopenhayn,1992)[23]的方法: (1)存在近乎无穷的潜在的市场进入者,这些潜在进入者在尚未决定是否进入之前可被视为无差别的; (2)决定进入市场的企业需要支付进入成本fe,然后它将会随机获得生产率φ,φ服从概率分布G; (3)在观察到自己的生产率水平后,企业决定保持生产或退出市场; (4)生存的企业每个时期均有δ的概率(由于受到某种冲击)退出市场。 在稳态均衡中,观察到自己生产率的企业要么会立即退出,要么每个时期都获得相同的利润π(φ)。因此,生产率为φ的企业的预期价值为: (37) 一旦知道φ*,就可以计算生存企业的生产率分布: (38) (39) 由此得到FE条件: (FE) 由此可知,FE曲线具有正的斜率。FE条件的意义是,对于既定的进入成本,企业越难以生存,则需要具有越高的平均利润。 (40) 由π(φ*)=0,r(φ*)=σf,可得: (ZCP) 第二个等式成立的原因是式(34)。此条件被称为零利润阈值条件(zero cutoff profit condition,ZCP)。 (41) 关于企业生产率的潜在分布G(φ),梅里兹(2003)[5]并未给出具体形式,但在其后续论文和大量相关拓展中,最常见的假定是φ服从帕累托分布,即: (42) 帕累托分布假定具有良好的说服力。首先,从经验角度它同企业规模的实际分布有很好的一致性。其次,从理论层面来说,在CES偏好假定下,使用帕累托分布将会使模型得到解析解。 2.开放经济 每个国家都同另外n个国家进行贸易,因此世界由1+n≥2个国家组成。为了突出生产率在企业出口决策中的作用和出口行为对企业生产率的反馈效果,梅里兹模型假定所有国家都是完全对称的。 企业在本国市场和外国市场的定价分别是: (43) 在本国市场和外国市场获取的收入分别是: rd(φ)=Rd(Pdρφ)σ-1,rx(φ)=τ1-σRx(Pxρφ)σ-1 (44) 由对称性假定,Pd=Px=P,Rd=Rx=R。令fx≡δfex,可以证明,每一时期由新进入出口市场的企业支付fex和出口市场中的所有企业在所有时期都支付fx是等价的。因此,企业在本国市场和外国市场获取的利润分别是: (45) 注意到,要素需求当中的固定成本f仍然存在,它被归纳到企业在本国市场的利润函数中。 π(φ)=πd(φ)+max {0,nπx(φ)} (46) 图4 企业生产率和其出口状态的关系 利用式(39),可以得到所有生存企业和出口企业的平均生产率分别为: (47) (48) (49) 同封闭经济一样,开放经济的加总变量也可以用平均生产率表示: (50) (51) (ZCP′) 从福利的角度看,由于在市场上竞争的企业(对于某国市场而言,竞争企业包括本国企业和外国企业)的平均生产率的提高,价格水平下降,所以实际工资提高,福利上升,贸易开放使参与国可以获得利益。从另一个角度来看,贸易开放使一些低生产率的企业被淘汰了,生存企业的平均生产率上升,这可以认为是另一种形式的贸易收益(8)关于价格水平下降和平均生产率上升的正式证明,可参见梅里兹(2003)[5]原始论文的附录部分。。 图5 企业生产率同利润和市场份额的关系 rd(φ) (52) 至于利润,由于rd(φ) 总而言之,贸易开放对不同生产率的企业产生了不同的效果。生产率最高的那部分企业通过出口获得了更大的市场份额和更高的利润;生产率较低一些的企业仍然可以通过出口获得更大的市场份额,但是在利润上会遭受一些损失;生产率更低的企业不会选择出口,只能在本国市场上销售,市场份额和利润都会受到损失;生产率最低的那部分企业由于不再能获取利润,被迫退出市场。 EK模型和梅里兹模型将贸易模型推向一个新阶段,贸易模型的微观基础越发坚实。企业异质性的内生化,使更细致的分析贸易的特征变得可行,并为微观数据应用于经验研究提供了理论基础。新贸易模型的出现加上大量微观数据的获取,使国际贸易领域的研究走入了更深的层次。在理论层面,异质性企业模型刻画了贸易对产业内以至企业内部资源配置的影响;在实证研究方面,利用微观数据可以研究出口企业的特征、出口产品种类等新问题。 然而,在国际贸易的研究中,有一个既古老又非常重要的问题,那就是参与国能否从贸易中获得利益;如果能,那么其获利是多大?从前面的内容可以看到,前者被所有的贸易模型定性确认,而后者则具有量化的含义,对其正式研究得益于贸易引力方程的发展。贸易引力方程从经验方程发展到具有微观基础的结构性方程,经历了长时间的过程。EK模型和梅里兹模型均可直接导出贸易引力方程,对模型本身和贸易引力方程的合理性起到了双向印证的作用。由于EK模型和梅里兹模型(9)实际上,克鲁格曼模型也可导出引力方程,正如之前介绍过的,梅里兹模型是对克鲁格曼模型的发展。具有可以直接将数理模型同贸易数据联系起来的良好性质,这两类模型(包括基于它们的大量扩展)被称之为量化贸易模型。 一个自然而然的问题是,这些“新”模型的出现是否会使对贸易利得有多大这个“旧”问题的回答产生变化。阿科拉克斯等(Arkolakis et al.,2012)[6]在一系列研究中对这个问题做出了否定的回答。 最早给贸易引力方程提出理论基础的是阿明顿(Armington,1969)[24],阿明顿模型现在被视为结构性贸易引力方程的基准模型。阿明顿模型非常简单,在需求侧,所有国家都具有对称的代表性位似(CES)偏好;在供给侧,每个国家都只生产一种商品,生产一单位商品使用一单位劳动力,劳动供给Li无弹性。所以,阿明顿模型在供给侧等价于纯禀赋经济。 j国对i国的进口额是: (53) 其中,wi是i国的工资水平,τij是i国和j国之间(对称的)贸易成本(冰山成本)。此方程即为最简单的贸易引力方程。 (WE) 因此,无论是何种冲击所致的福利变化,都可用λjj的变化推断出来(假定贸易弹性已知)。 阿科拉克斯等(2012)[6]在福利分析方面统一了一大类量化贸易模型,包括克鲁格曼模型、EK模型和梅里兹模型及很多扩展模型,由于这些模型可以导出具有相同形式的引力方程,因此也称其为“引力方程模型”。他们证明,只要贸易模型满足一些覆盖面十分宽泛的假定,阿明顿模型所导出的形式简洁的福利公式就仍然有效。也就是说,只要知道对本国产品的支出比例(11)在文献中,1-λjj也被称为贸易渗透率。、λjj和贸易弹性ε,就足以估计贸易利得。 其所考虑的满足福利等价性的贸易模型所需满足的假定包括: (1)CES偏好 每个国家都存在一个代表性消费者,此消费者具有Dixit-Stiglitz偏好,因此i国的综合价格指数即CES价格指数,得到: (54) (2)单一生产要素 这个模型集合假定仅存在一种生产要素——劳动,其禀赋为Li,价格为wi。单一生产要素也是目前大多数贸易模型,特别是基准模型所采用的假定。 (3)线性成本函数 在生产技术上,i国向j国出口ω商品的企业,其成本函数具备如下形式: (55) (4)市场结构 贸易模型通常设定的市场结构是完全竞争和垄断竞争,这两种市场结构都和阿科拉克斯等所描述的贸易模型集合相容。 要得到共同福利公式,贸易模型还需满足三个宏观层面的约束。 第一,贸易是平衡的。令Xij表示i国对j国的出口,则对任何j有: ∑i≠jXij=∑i≠jXji (56) 容易理解,只有在固定成本需要在进口国支付时,也就是β>0的情形,贸易平衡才有可能被打破。因此在完全竞争(没有固定成本)或者β=0时,这条约束自动满足;β>0时还需附加其他条件。 (57) 进口需求系统是CES的意味着贸易成本对相对进口需求的影响有对称和可分的性质。注意到每个贸易弹性刻画的是一对贸易伙伴i′和j之间贸易成本变化所引致的j国对i国的相对进口(j国对i国商品的购买占其对本国商品的购买之比)的(百分比)变化。式(57)表明,任意一对贸易伙伴之间贸易成本的变化对它们之间贸易额的影响都是对称的;同时,任意国家同第三方国家之间贸易成本的变化对Xij和Xjj有相同的比例影响。 需要指出的是,贸易额的变化既可能来自集约边际xij(ω)也可能来自广延边际Ωij,但贸易弹性是“宏观”层面的弹性,它总结了贸易成本变化对贸易额的总体影响,无论影响是来自集约边际还是广延边际。并且,式(57)是全局约束,在任意两个均衡之间计算贸易弹性,式(57)均应满足。 量化贸易模型可以得到等价的福利结论,是个非常强的理论成果。这个相当大的贸易模型集合中的模型具有不同的微观机制,它们对外部冲击对均衡的影响的刻画各不相同。简单如阿明顿模型,认为调整只发生在需求侧;而更现代的贸易模型所刻画的调整可能是劳动要素在部门间、部门内甚至是产品间的重新配置。证明了福利方程的普适性,就可以直接使用它进行贸易利益的定量计算,忽视冲击对经济影响的微观机制。这个方程具有极大的简洁性,所需的只有两个宏观层面的统计量,贸易渗透率和贸易弹性。 本文沿着贸易理论发展的历史脉络,通过梳理经典论文,介绍了新古典贸易理论、新贸易理论和新-新贸易理论的核心模型。在新古典贸易模型部分,本文首先归纳了新古典贸易模型所遵循的共同结论,介绍了新古典贸易模型的两个共性经典结论——贸易获利定理和比较优势定理,进而描述了李嘉图模型的经典数理模型——DFS模型,并简要介绍了H-O模型的核心结论。需要指出的是,H-O模型在现代国际贸易理论中已经很少作为单独的模型存在,但是其贸易导致资源在部门间重新分配的观点仍然占有重要地位。在新贸易理论部分,本文简述了克鲁格曼模型的核心思想。自克鲁格曼模型开始,CES需求系统成为了国际贸易模型的标准需求侧设定,本文对CES需求系统的特点和其成为贸易理论最受欢迎的需求设定的原因进行了探讨。 近些年的贸易理论领域,占据统治性地位的模型是EK模型和梅里兹模型。EK模型和梅里兹模型本质上具有不同的性质,EK模型遵循了新古典模型的假定,被认为是李嘉图模型在现代的复兴;而梅里兹模型是克鲁格曼模型的进一步发展,开创了新-新贸易理论的新局面。尽管如此,EK模型和梅里兹模型具有很大的共同性,它们都内生刻画了企业异质性,从而使得贸易模型和微观数据的发展相匹配。本文将这两种模型归并在一起进行了描述。 对贸易理论发展的另一条线索,也就是为贸易引力方程构建理论基础,近年来出现了突破性的进展。几乎所有可以导出结构性引力方程的贸易模型,最终可以在贸易获利的定量估计方面得出等价的福利方程。这个突破性的理论进展,不但为贸易模型和引力方程的合理性提供了双向印证,也使得对贸易利益的估计大为方便。 本文旨在通过梳理贸易模型的发展,归纳总结其一脉相承的共性和独具特色的性质,为研究者提供阅读经典贸易理论文献的线索,并为发展描述性更强、更具说服力的贸易模型提供方便。
(二)CES偏好在贸易模型中的应用


四、具有企业异质性的贸易模型
(一)EK模型






(二)梅里兹模型

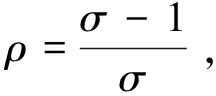
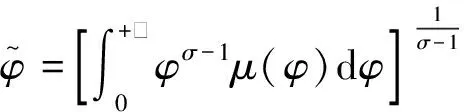





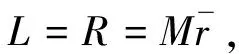







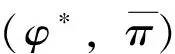


五、量化贸易模型的共性福利结论
(一)最简单的结构化贸易引力方程和福利方程


(二)福利公式的普适性
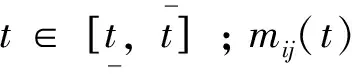


六、结语
