电动汽车无序充电的影响分析
2019-11-27郝越
郝 越
(深圳供电局有限公司,广东 深圳 518000)
0 引 言
随着技术的进步,电动汽车的数量正在不断增加[1]。同时,电动汽车作为移动式储能装置,在削峰填谷、提供电力系统辅助服务、协同消纳新能源等方面具有广阔的应用前景[2]。但是,电动汽车的无序充电可能会导致电网的峰谷差加剧、电压下降等不利影响,因此对电动汽车无序充电的过程进行分析尤为重要[3]。
由于电动汽车的型号和种类多样,主要分为交流1级、交流2级和直流充电电动汽车,其充电功率存在较大差别[4]。电动汽车的数量和充电功率对电网的影响不同,因此分析不同充电功率等级的比例,既能满足用户的需求在充电连接时长内获取预期的充电电量,也能减少设备投资,降低电动汽车无序充电负荷的峰谷差[5]。
为进一步优化电动汽车的充放电过程,文献[6]提出基于粒子群算法的电动汽车充电策略研究,以电动汽车电费最小为目标的充电策略,没有考虑电动汽车的充电功率影响;文献[7]针对电动汽车有序充电提出了原对偶内点动态优化算法,实现了以网损最低为目标的电动汽车充电模型求解,具有计算速度快、收敛性好的特点;文献[8]以充电功率为特征参量,研究了考虑充电桩利用率、充电等候时间、充电桩占地面积等因素的电动汽车充电桩优化设置,使得使用充电桩的社会成本最低。目前,以电动汽车的充电功率为目标的充电策略成果较少。
为此,本文以电动汽车充电功率为研究对象,采用多项式拟合的方法获得电动汽车充电量与时间的对应关系,从而获得电动汽车的负荷曲线。由于已接入充电的车辆其充电时间不会在负荷峰值处叠加,负荷曲线的峰值就会减小,因此采用拉格朗日乘数法建立优化模型,求解得到不同充电功率的电动汽车的占比情况。
1 电动汽车负荷曲线模型
电动汽车的充电时段与初始接入时间和连接时长有关。对于第一个时间段,假设起始时间是t0,终止时间是t1。为了简化分析,假设在这一个时间段内接入充电的车辆均在t0时刻接入。接入的车辆中,交流1级、交流2级、直流充电分别占比a、b、c,且a+b+c=1。各类型汽车的充电功率均按照给定功率范围的中间值计算。
由此,t0时刻接入充电的汽车总功率为:
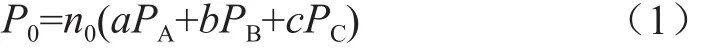
式中,P0为t0时刻接入充电的汽车总功率,n0为该时刻接入充电的汽车台数,PA、PB、PC分别为交流1型、交流2型、直流型汽车的充电功率。
在得到t0时刻接入充电的汽车总功率P0后,可以计算该时刻接入的汽车所需要的充电时长:

式中,h0为t0时刻接入充电的汽车所需的充电时长,Q0为该时刻接入的汽车所需的充电电量。同样地,可以得到第二个时间段,即t1时刻接入充电汽车的总功率P1和充电时长h1。
在获得第一个时间段和第二个时间接入充电的汽车分别需要的充电时长h0、h1后,比较t0、t0+h0、t1、t1+h1的关系,即可得到第一个时间段和第二个时间段的负荷分布情况:当t0+h0<t1时,则第一个时间段内的负荷功率为P0,第二个时间段的负荷功率为P1;当t1<t0+h0<t2时,则第一个时间段内的负荷功率为P0;第二个时间段内,t1~t0+h0时段的负荷功率为P0+P1,t0+h0~t2时段的负荷功率为P1,由于划分的时间段较小,可以在具体求解过程中粗略认为第二个时间段及t1~t2时段的负荷功率都为P0+P1。
上述过程仅考虑了两个时间段的情况,事实上对任意一时间段进行负荷分析时,均需要考虑前面所有时间段对该时间段的影响。
对于第n个时间段,假设前m(m<n)个时间段内接入充电车辆均对该时间段有影响,即在tn-m-1、tn-m…tn-2时刻接入充电的电动汽车,再加上其充电时间hn-m-1、hn-m…hn-2后,均大于tn-1。此时,第n个时间段的负荷功率为Pn-m-1+Pn-m+…+Pn-1,如图1(a)所示。
若中间某一个时间段内接入充电车辆均对该时间段未对该时间段造成影响,则可剔除该时时间段内接入充电车辆的充电功率。例如,若前k个时间段未对第n个时间段造成影响,则第n个时段负荷功率为Pn-m-1+Pn-m+…+Pn-k-2+Pn-k…+Pn-1,如图 1(b)所示。
在上述模型中,对任意一个时间段i均有两个量是未知的,即每个时刻接入的汽车所需的充电电量Qi,每个时刻接入充电的汽车数量为ni,故需要确定Qi与ni。
(1)ni的确定。在已经得到了每个时刻接入充电的车辆数与时间的概率分布情况后,即得到了n随t的概率密度曲线法f1(t),利用f1(t)可以求出车辆在第i个时间段内充电的概率:
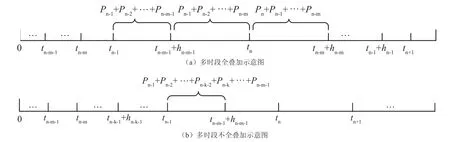
图1 多时段叠加示意图
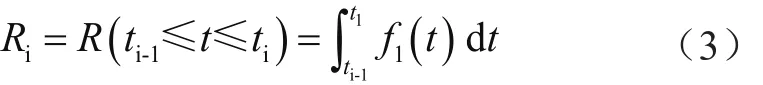
式中,Ri表示汽车在第i个时间段内充电的概率,N为汽车总数,且ni=NRi。
(2)Qi的确定。同n一样,若能获取Q随时间的分布特性,则可以较容易获得各个时刻接入充电的汽车所需的充电量,故需利用已知数据构造出Q与时间的分布关系。在已知数据中,分时段统计该时段内接入充电的汽车台数与充电量,若在第i个时间段内统计得到的汽车台数为m台,相对应充电量分别为Qi,1,Qi,2…Qi,m,则可以求出:

式中,为该时间段接入充电的汽车的充电量的均值,用以模拟该时间段所有接入充电的汽车的充电电量。
在获取所有时间段的充电电量均值后,即可利用均值拟合出充电电量与时间的关系曲线fQ(t)。虽然是用各个统计时间段内的均值模拟的充电电量与时间的关系,但是均值可以充分反映样本总体的数值大小。此处需要求解总体的负荷特性,而非单个电动车的负荷特性,所以是合适的。
获得充电电量与时间的关系曲线fQ(t)后,即可获得任意一时刻电动车的充电电量。由于调度时通常是每过一个时间段(通常为15 min),即对电网的运行状态进行依次评估,所以关注的往往也是该时间段所需用电量的均值,即:

通过式(5),即可获得每个时间段接入的汽车所需的充电电量Qi。
2 充电功率等级比例优化模型
在保证用户需求的前提下,通过改变不同类型充电功率等级的比例,可以有效降低电动汽车无需充电负荷的峰谷差,改善电力系统的运行状况。但是,随着不同充电功率设备比值的变化,充电站的投资必然有所改变。需要寻找合适的比例,使峰谷差降低的同时,充电站的投资并不出现剧烈的增加。
通过分析可以发现,负荷随时间的分布与电动汽车接入量随时间的分布具有强烈的相关性,所以负荷的峰谷也出现在电动汽车接入量的峰谷处。本文模型是使用时间段的叠加量来表征负荷功率的大小,如果保证在负荷峰值周围的时间段都不叠加,即可减小峰值处的负荷功率。根据这个思路建立相应的优化模型。
设α、β、η分别为交流Ⅰ型、交流Ⅱ型、直流型充电设备负荷所占比例,为了使峰值处不产生充电时间的重叠,则:
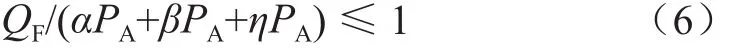
假设交流Ⅰ型、交流Ⅱ型、直流型充电设备每台的成本为C1、C2、C3,则总的建设成本为:

式中,M为充电桩总数。由于总数一定,M的大小只会导致制造成本成比例增加,极值点所在位置的α、β、η值不会改变,所以可以建设成本中去掉M,对求解极值点的α、β、η值不会造成影响,则建设成本的表达式可以简化为:
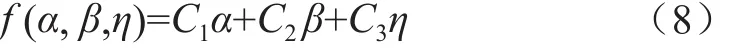
在式(6)中,等号左边所得值越小,则高功率设备所占比例越大,建设成本也就越高。为达到减少建设成本且降低峰谷差的目的,所以将该式的值取1,即:
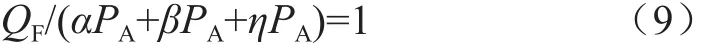
式(9)为式(8)的一个约束条件。对式(8)求极值,可以建立一个基于拉格朗日乘数法的模型:
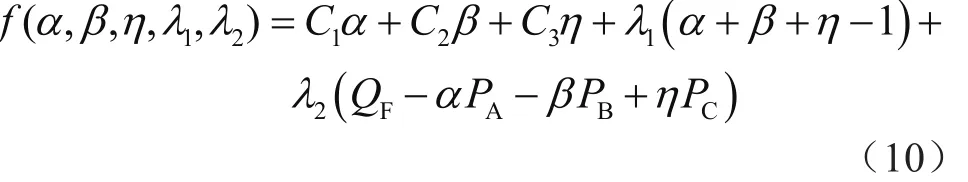
对式(10)求偏微分,且令偏微分结果为0,即:
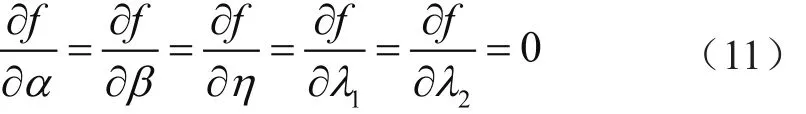
求解方程组,即可得到合适的α、β、η。
3 算例分析
电动汽车的功率主要分3个等级,相关参数如表1所示。选取1 h作为时间间隔,对电动汽车的充电电量与时间关系进行统计分析。数据选用2018届电工数学建模A题附录1中的数据。
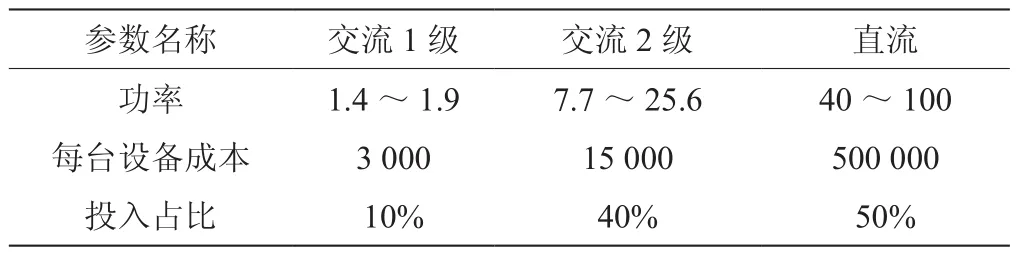
表1 不同功率电动汽车的相关数据
采用多项拟合的方法,得到充电电量随充电时间的变化曲线如图2所示,函数表达式为:

其 中,fQ(t)为汽车充电电量,p1=-6.43e-7,p2=0.002 1,p3=-0.035,p4=0.28,p5=-0.95,p6=0.087。

图2 电动汽车充电量与时间的关系
由图2可看出,在夜间0:00-5:00、18:00-24:00时段内,电动汽车不行驶,可以长时间充电,此时段内电动汽车的充电量较大。白天时段内车主要用车,电动汽车不能长时间连接充电桩,此时段内充电量较小,充电量在此时段内随时间平稳波动。
利用得到的充电电量随充时间变化的函数表达式,计算出每个时刻的充电电量Q,同时利用充电车辆数随时间变化的概率密度曲线,计算各个时刻接入充电的汽车数量n,结合模型,即可求解各个时间段的负荷功率,具体数据见表1,负荷随时间的变化曲线如图3所示。
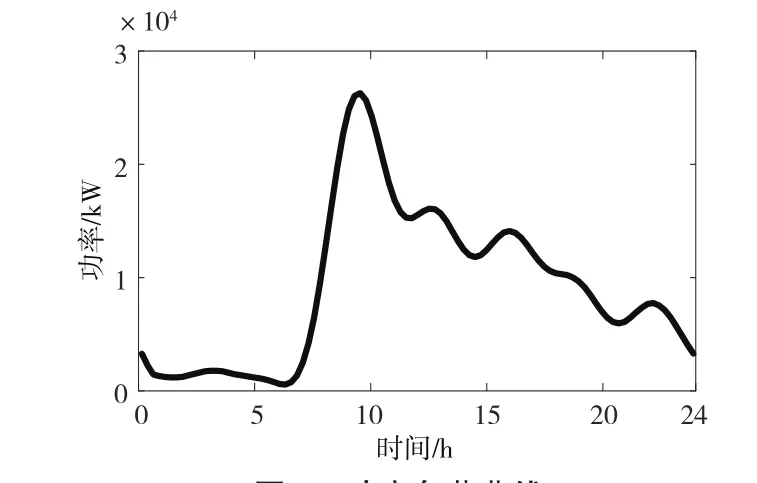
图3 功率负荷曲线
从图3可以清楚看出一日内负荷功率的变化情况。从0:00-6:00,负荷一直处于低位运行,其中0:00-1:00呈现下降趋势。结合电动汽车的运行特征分析可以发现,在0:00-6:00这个时间段内,接入充电的电动汽车数量很少,即使每一台接入充电的汽车的充电电量最大,总的充电功率依然很小。而导致0:00-1:00呈现下降趋势的原因主要包括两方面:一是接入充电的车辆数减少,二是前一天接入充电的车辆到这个时间段基本上都已经充到了理想的充电电量,不再对这一时间段的功率造成影响。6:00-10:00负荷功率陡增,这个时间段电动汽车行为变得活跃,人们上班等活动均导致电动汽车自身的用电量减少,电动汽车需要冲电的倾向显著。所以,这一时间段接入充电的车辆数明显增加,即使每台车的充电电量不是很大,负荷功率依然会出现明显的上升趋势。每个时刻接入充电的车辆相互叠加影响,导致负荷功率上升的趋势十分明显。10:00以后,负荷功率呈现有起伏的下降趋势。10:00左右负荷功率到达峰值后,每个时刻接入充电的汽车数量逐渐减少,这是由于之后的时间段不会出现早上拥堵式的汽车接入,人们对电动汽车的使用也不会像早上上班这样密集。在明显的活跃期,如12:00、14:00-15:00、17:00以及21:00等汽车活动的活跃时段,又呈现出上升趋势。此外,晚高峰也是电动汽车使用的高峰期,但是在从当日晚高峰后到第二天早高峰前比较宽裕的时间段进行充电,负荷不会出现陡增的现象。此外,负荷功率和电动汽车接入数量有着类似的分布。
电动汽车为1万辆时,其负荷峰值为25 764 kW·h;当电动汽车数目为 307时,QF为83.92 kW·h。PA、PB、PC采用中间取值的方法,通过拉格朗日乘数法可计算得到交流1型、交流2型、直流型充电设备负荷所占比例分别为α=0.312、β=0.627、η=0.063。
4 结 论
在无法直接求得充电功率的情况下,本文利用充电电量求取各个时刻接入充电的车辆所需的充电时间,利用充电时间的叠加间接求出充电功率,获得负荷曲线。结果表明,在10:00时电动汽车的充电负荷最高。考虑到前面时刻接入充电的车辆的充电时间不会在负荷峰值处叠加,负荷曲线的峰值会减小,利用拉格朗日乘数法建立优化模型,求得3种功率充电设备的占比分别为0.312、0.627、0.063。
