直观把握数学本质 动态提升思维品质——从教材中一个立体几何问题例谈变式教学

李 健

(江苏省外国语学校 215104)

随着社会的飞速进步与科学的迅猛发展，人们对数学的认知不再停留于“工具”层面，而是将其视为改变思维方式的重要途径，这就要求高中数学老师必须将这种变化融入到日常的教学中.章建跃博士认为：数学教学的主要目标就是使学生在获得“四基”和“四能”的过程中发展思维能力.[1]这与变式教学中“通过不断迁移问题的非本质属性、不断变更思维角度来把握问题本质、提高思维能力”的教学模式不谋而合.新课标中指出“直观想象是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础”.[2]所以笔者借助于教材(苏教版必修2)51-52页“阅读”中的一个立体几何问题，以课堂教学为呈现方式，例谈变式教学在高中教学中如何有效提升学生的数学思维品质的.

1 教学背景概述

在必修2立体几何这一章学完后，针对高一学生的学情和特点，笔者设计了一个微型专题，将立体几何中一些常见问题的解决思路嵌入至“正四面体”和“正方体”这两个最常见的直观载体中，以期引导学生梳理立体几何中的重难点定理和应用，深化学生对“点、线、面”位置关系的认知，从而达到“示以思维之道”教学目的.

2 课堂教学实录

2.1 设置变式情境，培养类比思维方式

师：各位同学，在平面几何里有这样一个问题：【问题1】“若P是边长为a正三角形内一点，求P点到该三角形三边的距离之和”.你能给出解题思路吗？

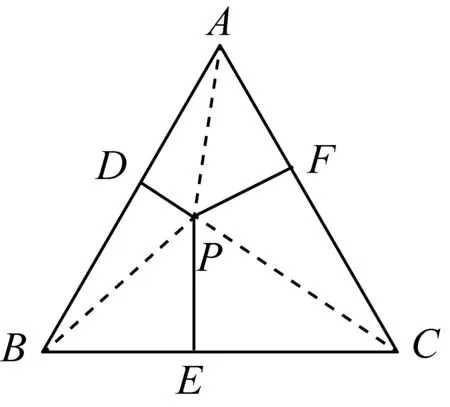
图1

师追问：从中你可以看出有何种结论？

生：正三角形内任意一点到三边的距离之和是一定值，为正三角形的高.

师：很好！下面我将该问题提升一个维度，【问题2】“若P是棱长为a正四面体内一点，求P点到该四面体四个面的距离之和”，首先，对于正四面体，大家能否猜想出一个类似的结论？

生：正四面体内任意一点到其四个面的距离之和为一定值，且该定值为正四面体的高.

师：回答的非常好！刚才这位同学在猜想该结论时利用了“类比”的思维方式，即根据这两个对象在某些方面的相同或者相似之处推断出它们在其他方面有相同或相似点，这种创造性的思维方式值得表扬，但其真实性是否可靠还需要大家来进行探究.

(学生进行思考和互动讨论)

生：依然可以“类比”，利用“分割法”和“等积法”解决问题.如图(图2-1)，设正四面体的一个表面正三角形面积为s，高为h，P点到四个表面的垂线段分别为PE、PF、PG、PH，连接PA、PB、PC、PD可将正四面体ABCD分割成四个小三棱锥，再利用“等(体)积法”解决问题：

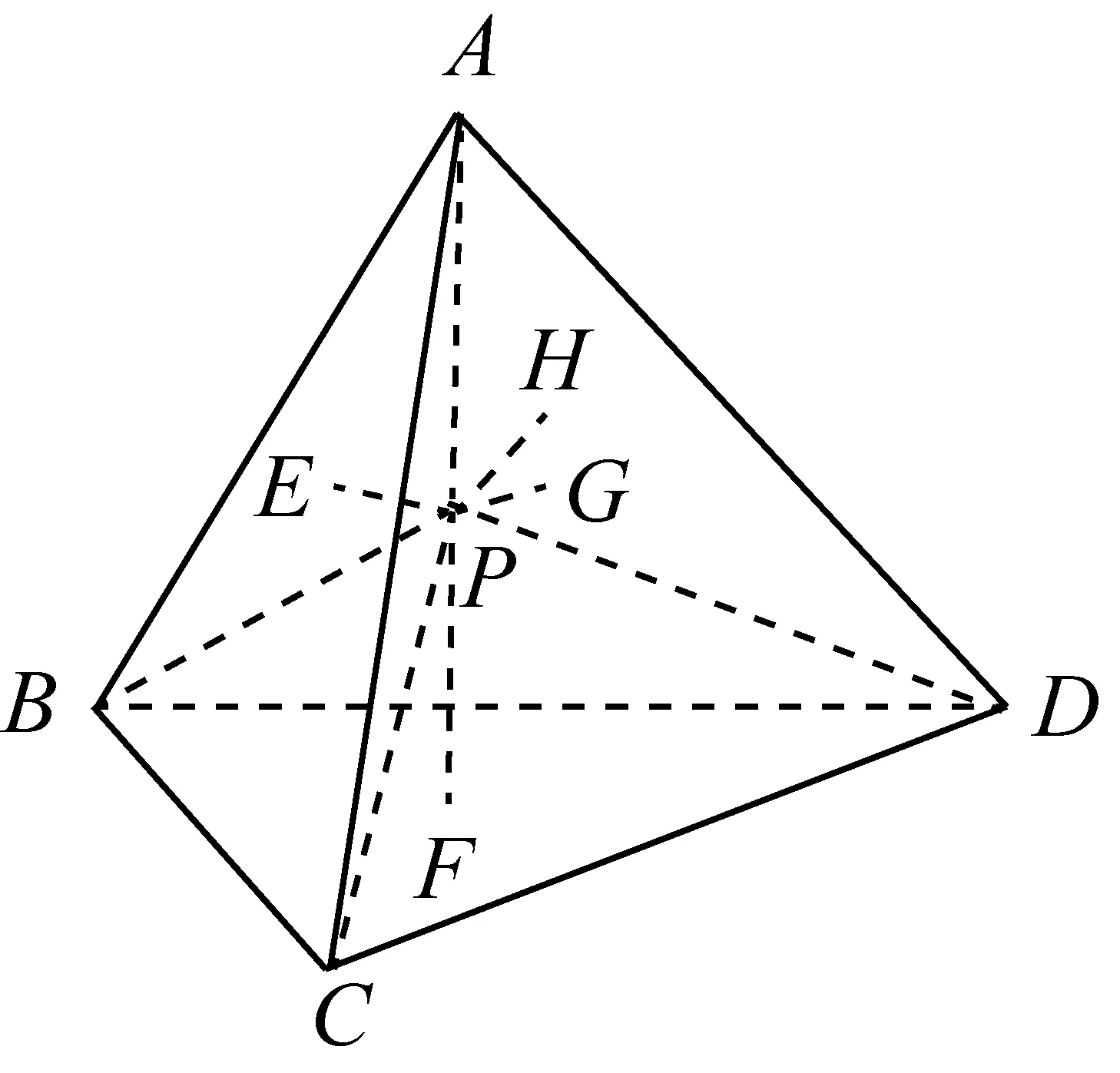
图2-1

VABCD=VP-ABC+VP-ABD+VP-ACD+VP-BCD

⟹PE+PF+PG+PH=h.

师：非常好！接下来如何求出正四面体的高h呢？

生：连接点A与底面正三角形中心O(图2-2)，OA即为正四面体的高，

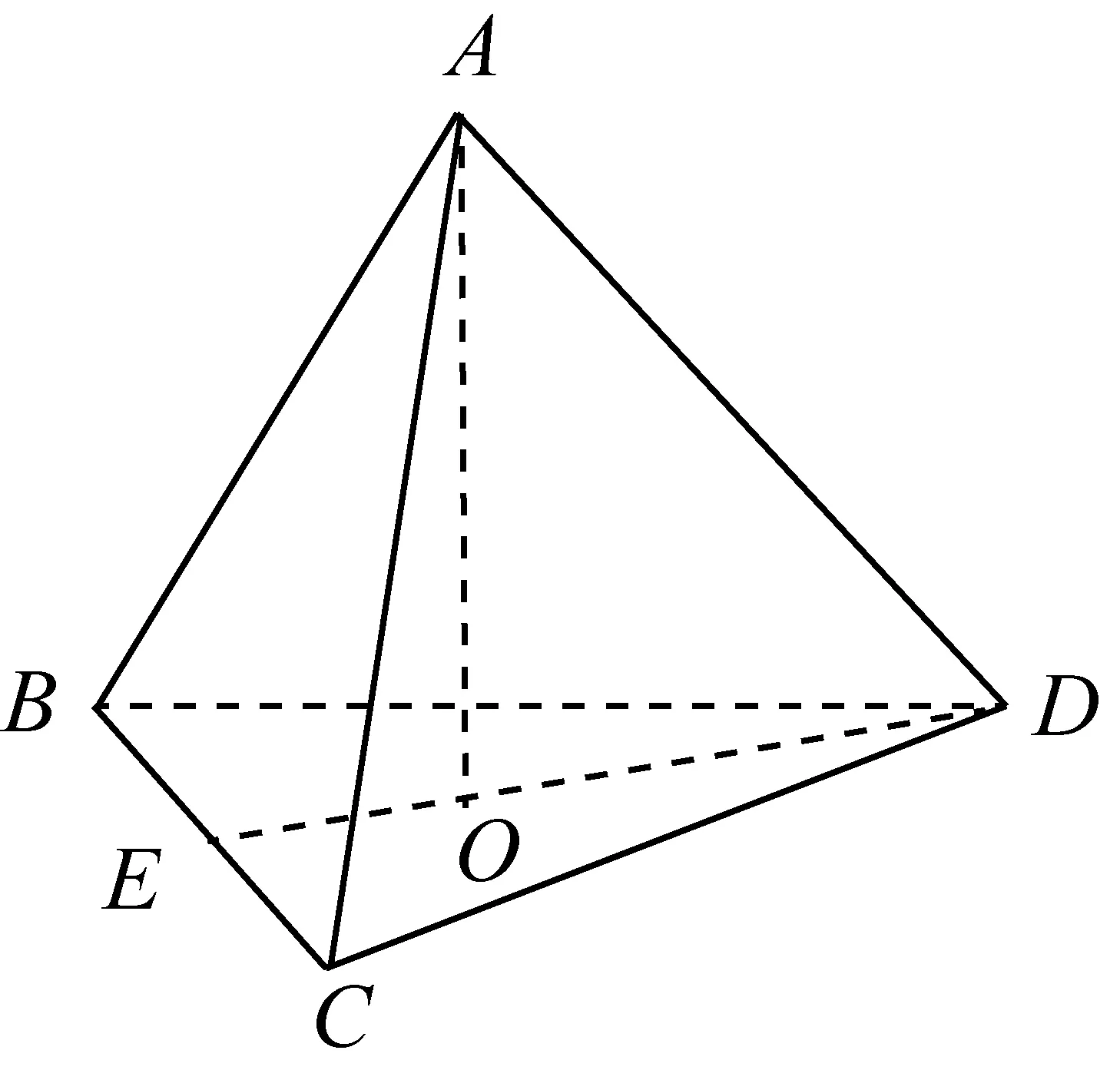
图2-2

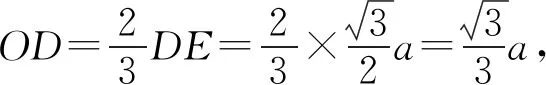
2.2 深化变式题型，提升形象思维能力

师：接下来继续探讨正四面体：【问题3】已知正四面体的棱长为a，求其内切球的半径.

生：如图(图3)，设内切球O与正四面体的各个面的切点分别为E、F、G、H，则根据上个问题的结论，不难得出：

图3

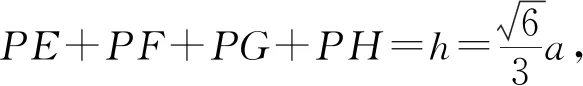
且PE=PF=PG=PH=r(r为内切球半径)，

师追问：如果要你求其外接球的半径呢？(变题：【问题4】已知正四面体的棱长为a，求其外接球的半径)

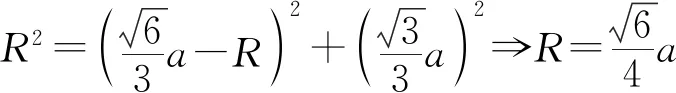
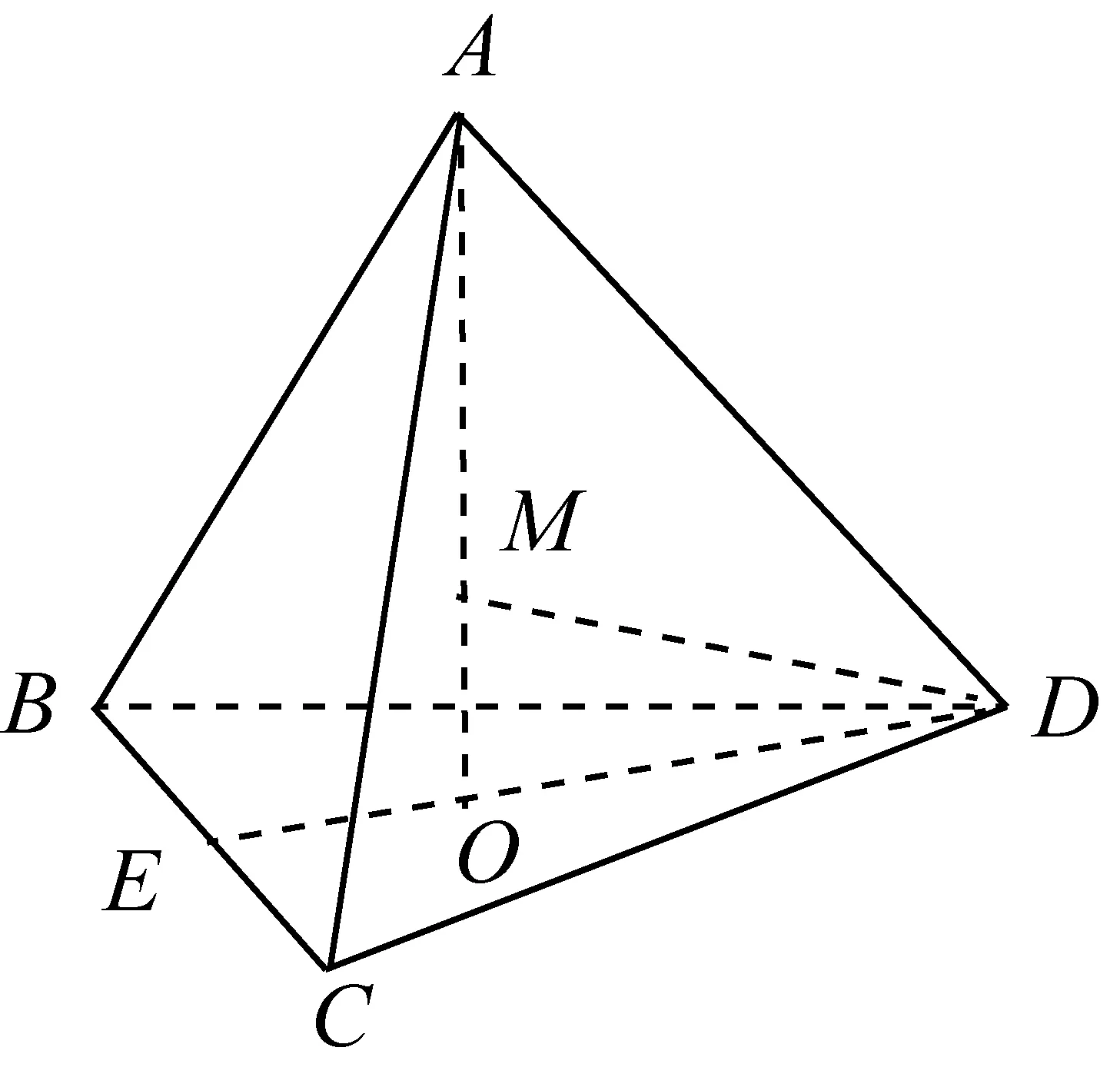
图4-1

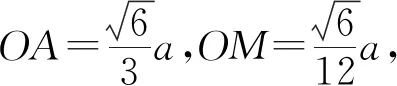
图4-2

师：上述3位同学解决问题的过程都很精彩，甲、乙两位同学解决问题的思路是对问题2、3的思维延续.而丙同学则另辟蹊径，将“正四面体‘嵌入’至正方体中”，相较于之前的“分割法”这里他采用的是“补体法”.总而言之，“割补”的思维途径也是我们解决立体几何问题的有利武器.

2.3 串讲变式解法，激活发散思维热情

师：感谢丙同学为我们开辟了一条研究正四面体的新的思维通道，接下来我们借助于这个正四面体的“好兄弟”——正方体，来重新审视我们之前研究的问题：【问题5】正方体ABCD-A1B1C1D1棱长为a，求四面体AB1CD1的体积.

生：首先，易得出四面体AB1CD1为一正四面体，可以类比之前解决问题的思维方式，利用“割补法”解决问题(图5)，即用正方体的体积减去四个完全全等的三棱锥的体积

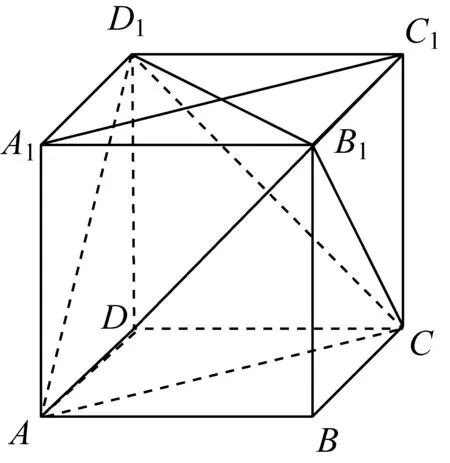
图5

师：很好！沿着这条思路，你是否找到一种求正四面体AB1CD1高的解题方法？

师追问：你能发现正四面体AB1CD1的高与正方体ABCD-A1B1C1D1体对角线的长度关系吗？

师：【问题6】观察图6，结合本章所学的知识和上述研究的结论，请大家探究图中的平面AB1D1与平面BC1D都包含哪些几何性质，你能否给出证明过程？

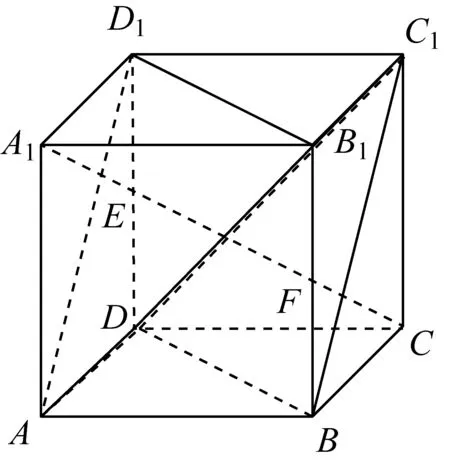
图6

生：(1)结合正方体的几何性质，通过“面面平行的判定定理”可证得平面AB1D1平行于平面BC1D；(2)根据正方体的几何性质和“线面垂直的判定定理”可证得平面AB1D1、平面BC1D与正方体对角线A1C垂直；(3)利用问题5的结论可得到平面AB1D1和平面BC1D将正方体对角线A1C三等分.

师：上述探究出来的结论(1)(2)的证明过程请大家课后完善，接下来请你根据结论(1)(2)探寻一条得到问题5结论的新思路.

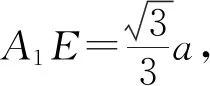
师：非常好！上述的一系列解决问题的过程帮助我们找到了又一条求正四面体高的简捷途径，即为所“嵌入”正方体对角线的三分之二，并让我们直观感知了正四面体与正方体的“亲密关系”，同时拓展了一类问题的解题思路，例如本节课多次涉及的“分割和等积”，可谓“一石三鸟”！

2.4 反思变式过程，构建动态思维导图

师总结：回顾刚才的探究过程，我们不难发现，对于同一个问题我们可以从不同角度去审视，采用多种方法、多种途径去解决；同样，多个具有相同或者相似特质的问题，我们可以通过挖掘其共性，找到贯穿这类问题始终的解题思路，把握其“题根”，也可以用同一种方法去解决.如此一来，便动态生成了我们本节课思考问题的脉络，我用如下的思维导图进行呈现：

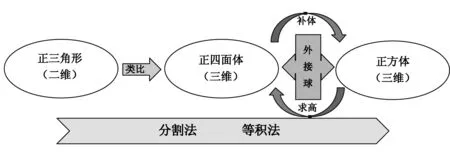
3 课后教学感悟

3.1 一题多解——变式教学激发思维活力

美国著名的数学家波利亚认为：掌握数学就意味着善于解题，希望提高学生解题能力的教师，必须培养学生的兴趣.“一题多解”是得到广泛认可的提升学生解题兴趣和思维能力的变式教学模式.笔者在本节课的授课中，明显感受到了学生的两个思维热情高点，一是在探究问题4时，丙同学新颖的解题思路点燃了不少同学的思维热情；二是利用问题6得出的几何结论，再通过思考探究得到“求正四面体高”的又一方法时，不少同学流露出兴奋的情绪.从浅层面的表象来看，学生对于追求新颖、简便的解题方法充满了浓厚的兴趣，是一种天性和本能；但从深层次的角度分析，其实是教师通过教学设计，利用求异思维和辐射思维帮助学生冲破了思维定势的束缚，给与了学生持续思考的动力.正是注入了这股思维活力，往往会驱使我们的教学过程由“一题多解”最终转变为“一题优解”，从而实现教学效果的进一步优化.

3.2 多题一解——变式教学把握思维本质

本节课中，笔者设置了一系列变式题组，研究的主体对象也发生了两次变化，即正三角形变成了正四面体，正四面体又变成了正方体.但是在教学过程中笔者发现，无论是研究对象的维度发生了变化还是所要解决的问题发生了变化，学生都可以在思考探究的过程中感知三者的共同之处，并自觉不自觉地用同一种思维方式去发现它们的内在联系.“类比”、“割补法”和“等积法”之所以能贯穿始终，是因为从思维的角度，学生都在努力从不同层面去类化它们，这符合高一学生的认知规律.所以在数学教学中，也可以利用“多题一解”的变式教学途径，类化不同变式的共同属性而突出问题的本质属性.[3]

3.3 师导生究——变式教学理清思维脉络

新课标倡导要将培养“自主与创新”意识渗透到教学活动的各个环节，但这不意味着教学活动是“信马由缰”.所谓“道而弗牵”，教师应该是用“引导学生探究”来替代“牵着学生走”.该微专题的目标指向性比较明确，即以学生熟悉的三个几何体为载体，设置问题串引导学生探究其几何共性，不是“为了解题而解题”，而是在探究问题的过程中动态升华其直观思维.例如设置变式问题4，目的是引导学生借助“外接球”这个思维纽带将正四面体与正方体有效地桥接在一起，承上启下地探究两者的共同属性.数学的价值常常处于“潜形态”，这就需要教师采取必要的教学措施和具体的教学手段，通过不懈的努力让学生真正体会到、感受到.[4]这也是教师不断引导学生自主探究的意义所在.

数学学科核心素养本质上反映的是数学的思维品质，基于核心素养的数学课堂应立足于学生思维品质的培养而成为“思维之树常青”的课堂.[5]把握问题的本质使“思维之树”的主干坚韧挺拔，思维的动态迁移让“思维之树”的枝芽青葱繁茂，这种“不变”与“变”的辩证统一正是变式教学的魅力所在.