圆心角定理教材设计的思考与反思

张安军

【摘 要】现行人教版九年级（上）“弧、弦、圆心角”中，用圆形纸片探究圆的旋转不变性，学生感悟不深，后继难以发现弧、弦、圆心角之间的关系.基于定理教学思路的自然性构建问题设计教学，让学生经历定理的自然合理的发现和证明.

【关键词】 弧、弦、圆心角;教材研究;教学设计

人教版九年级（上）“§24.1.3弧、弦、圆心角”一课中，教材先让学生进行探究：“剪一个圆形纸片，把它绕圆心旋转180°，所得的图形与原图形重合吗？由此你能得到什么结论？把圆绕圆心旋转任意一个角度呢？”教材试图通过学生动手操作，发现圆不仅是一个中心对称图形，而且圆还具有旋转不变性，然后利用圆的这一性质，探索圆心角定理.事实上，学生能体悟到圆是中心对称图形，但对于圆的旋转对称性体悟是不够的，按教材的思路进行教学时，亲身的课堂实践或其它老师的公开课中，发现学生很难利用圆的旋转对称性发现圆心角、弧、弦之间的数量关系，更有甚者，老师利用圆的旋转对称性证明这一定理，学生也很难理解，感觉这个证明“怪怪的”.可见教材中这一教学设计不能很好体现认知的合理性、思维的自然性.

1 基于思路自然性的教学设计

教材中对圆的旋转不变性，仅仅让学生旋转一张圆形纸片，马上得出圆具有旋转不变性，然后再利用旋转不变性让学生探索弧、弦、圆心角之间的数量关系.由于学生对圆的旋转不变性还没有准确的理解，试图让学生利用这一性质去探索弧、弦、圆心角的关系，教学的实效性大打折扣.事实上圆的旋转对称性在这里起到承上启下的作用.承上是因为在这之前研究过垂径定理，垂径定理体现了圆的轴对称性，除了圆的轴对称性外，圆还具有旋转对称性;启下是因为圆具有旋转对称性，可利用这一性质让学生发现圆心角定理，即弧、弦、圆心角之间的关系.可见对于圆的旋转对称性构成了这节课的关键所在.教材中让学生操作一张圆形纸片，试图得出圆具有旋转不变性，在常人的眼里，圆的旋转不变性太简单了，其实不然，学生对概念的理解需要经历从过程到对象的凝固，需要思考，更需要沉淀.圆的旋转不变性的理解也一样，圆的旋转不变性要基于两个图形旋转后的比较.其次要建立旋转前后图形对应关系，表现在图形前后点与点之间的对应关系.教材中仅让学生通过一张圆形纸片的旋转操作试图得到圆的旋转对称性还是不够的，把一个图形在空间中想象成两个图形，学生是有困难的.因此在理解教材的基础上，要个性化或者创造性的开发教材，让课堂教学变得实效.基于上述的思考，对于圆心角、弦、弧的关系，教学中一方面让学生自然而然想到圆具有旋转对称性，另一方面自然地利用旋转对称性发现并证明圆心角定理.基于两方面的思考给出以下教学设计，供同行们参考.

问题1 上一节课我们学习了哪些内容？

追问1：垂径定理刻画圆的什么性质？

追问2：圆除了轴对称性外，圆还有其它性质吗？

教学预设 在学习“弧、弦、圆心角”关系前，先让学生回顾上一节课的内容，即垂径定理，在这个定理中共有5个量，一般地已知2个量，就可以推出其它3个量.然后追问学生该定理体现了圆的什么样性质？若学生有困难时，可以启发学生我们是如何证明该定理？圆除了轴对称外，圆还有什么特别的性质呢？继续激发学生探究的热情.

设计意图 回顾垂径定理，一方面从圆的轴对称引出圆的旋转对称，另一方面本节课的“圆心角定理”共有3个量，已知1个量，就可以推出其它2个量，该定理的内容和证明都和“垂径定理”类似，为后继的类比作铺垫.

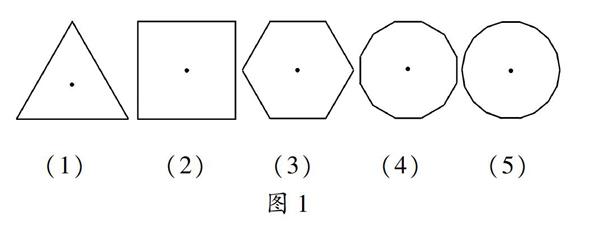
问题2 如图1（1）—（5），正n边形绕其中心至少旋转多少度能与原图形重合？

追问1：随着n的增大，正n边形会趋向什么样的图形？

追问2：圆绕圆心旋转多少度可以与其自身重合？

追问3：圆除了中心对称图形外，圆还具有什么样的特性呢？

教学预设 从特殊的正三角形开始，让学生先说出正三角形绕其中心旋转多少度还能与原图形重合，然后慢慢从正方形、正六边形拓展到正十二边形、正二十四边形，最后拓展到正n边形，让学生猜想随着边数无限的增加，正n边形会趋向什么图形.在这一变化过程中，让学生体悟到圆繞圆心任意旋转一个角度都能与自身重合.然后追问学生何谓中心对称图形，即绕中心旋转180°能与自身重合，那么能否推广这一概念，结合正n边形，把中心对称图形的旋转的度数从180°推广到120°、90°、60°等等，更一般地得到旋转对称图形概念，圆不仅是中心对称图形，更一般地圆是旋转对称图形.

设计意图 从正三角形拓展到正n边形，随着n的增大，正n边形趋向圆，从具体到一般，从感性到理性，让学生从正n边形变化过程中自然而然感悟圆的第二个性质，即圆具有旋转对称性.

问题3 如图2（1）—（3），等边△ABC（正方形ABCD、正六边形ABCDEF）绕中心点O旋转∠AOB能与自身重合.根据∠AOB位置特征，请你给这样的角一个贴切的名称？

追问1：如图3，你能给圆心角下一个定义吗？

追问2：如图4，判别下列（1）—（4）哪些角是圆心角，并说明理由.

教学预设 教师先让学生观察等边△ABC（正方形ABCD、正六边形ABCDEF）中的旋转角∠AOB，然后根据其位置特征的共同点，抽象概括得出图3中的∠AOB，从中归纳出圆心角的概念，角的顶点在圆心取名为圆心角.在学生辨别圆心角的概念后，引导学生反思圆心角的概念的关键点是角的顶点在圆心.

设计意图 引导学生关注观察正n边形的旋转角，根据旋转角的位置特征，从特例中归纳出圆心角的概念，圆心角的概念基于数学内部自然地产生.

问题4 “垂径定理”体现了圆的轴对称性，圆还是旋转对称性图形，那么圆还有别的性质吗？观察图5和图6，你发现了什么？

追问1：你能把自己的猜想推广到更一般吗？

追问2：你能对自己所发现的结论加以证明吗？

教学预设 先让学生观察图5（1），然后谈谈自己的发现，学生可能会发现角相等，如：∠AOB=∠COB=∠COD=∠AOD=90°;可能会发现弦相等，如AB=BC=CD=DA;也可能发现弧相等，AB=BC=CD=DA，然后再剥离图5（1）—（2），图5（2）中两条直径垂直，即∠AOB=∠COD=90°，你还会得到些结论呢？同样引导学生继续观察图6（1）—（2），在此基础上，让学生从特例中归纳出一般的结论，并对自己提出的猜想加以验证.

再引导学生站在整体、系统的角度思考这个问题，这个系统中共有三个量，若一个量为已知（如圆心角相等），就可以得到其它2个量相等，用基本量的思想再次引导学生提出问题、分析问题和解决问题.

设计意图 从特殊的正方形和正六边形中观察它们相应的圆心角、弦、弧之间的数量关系，然后分离变量，继续引导学生观察，学生经历从朦胧到模糊，从模糊到清晰，圆心角定理的提出和证明水到渠成又自然合理.

（圆心角定理的应用及其小结略）2 教学反思

2.1 理解教材的整体结构，做好教学设计的起点

圆的有关性质这一单元教材先定义圆的概念及其弧、弦等相关要素，然后折圆形纸片发现圆是一个轴对称图形，利用圆是轴对称图形进一步引导学生发现垂径定理.本节课弧、弦、圆心角的引入也是先让学生操作圆形纸片，发现圆是一个中心对称图形，进一步操作该纸片，圆不仅是中心对称图形，圆还是旋转对称图形，利用圆的这一性质继续引导学生发现圆心角、弧、弦之间的关系，具体地本单元的知识结构如图8所示.

可以发现，教材的编者是基于整体的观念编写教材，通过圆的不同对称性来探究圆的性质，而具体在本节课中，教材通过旋转圆形纸片让学生感受圆具有旋转对称性.圆的旋转对称性不同于轴对称性，轴对称及其性质教材在八年级上进行学习过，而旋转对称的概念是一个新的概念，教材虽然没有提及旋转对称概念，但是后继却利用这一性质去探索圆心角、弦、弧的关系.因此在教学设计时，既要站在教材整体角度理解教材思路，又要站在微观的角度思考本节课前后知识的关联性设计教学.具体地在本节课中只有学生理解了圆的旋转对称性之后，弦、弧、圆心角之间的数量关系才能水到渠成.为了让学生形成圆的旋转对称概念，在学生最近发展区提出正多边形至少旋转多少角度才能和自身重合，从具体到一般，感性到理性，随着正多边形的边数增加，旋转的度数越来越小，而正多边形越来越趋于圆，在正多边形和圆的变化过程中，学生自然而然感受圆的这一特性，圆不管旋转多少度数都能自身重合.为后继探索圆的性质作了很好的铺垫.

2.2 寻找定理发现的自然思路，发挥定理教学的育人价值

数学定理的产生与发展应是自然合理的，但教材中的许多定理以直接的方式呈现，省略了定理产生和发展等过程的介绍.在教学中如果将这些定理直接强加给学生，不仅会让学生感到定理来得突然，也不利于对定理本质的理解.因此在定理教学中设计合适的思路，有效地让学生经历探索的过程，在探索过程中能有效地培养学生提出、发现问题的能力以及分析和解决问题的能力.那么教师如何设计才能最大实现定理教学育人价值呢？大教育家夸美纽斯就指出：“要使所用的方法能够激起爱好知识的心思，它第一就需来得自然.因为自然的事情就都无需强迫.水往山下流是用不着强迫的.”从数学知识发生发展过程角度看，要合乎数学知识本身的逻辑结构和发展规律;从学生思维和认知的角度来看，要符合学生的认知规律和心理特征.前一个的核心是数学的学科思想问题，后一个是学生的思维规律、认知特点问题.

2.2.1 遵循逻辑关系，促进知识的自然生长

定理是揭示和反映数学概念本质属性及属性间联系的一种重要形式，教师要深入理解定理的本质，清晰定理的数学逻辑起点，理清定理中知识点间逻辑关系，自然而有机地展开知识的画面，促进知识在学生原有知识基础上自然地生长.例如圆周角定理是体现圆的旋转对称性.圆的旋转对称性是构成圆心角定理的逻辑起点，而旋转对称性是中心对称性的一般化，因此在本节课教学中，從中心对称图形出发，正多边形旋转的角度从180°拓展到一般的度数，在这个过程中，发展学生抽象、归纳、一般化等思想.当学生深刻理解了圆的这一特性，让学生探索圆心角、弧、弦的数量关系，寻找知识间的联系，新知识的生长就显得自然合理和水到渠成.

2.2.2 遵循认知特点，促进知识的新生长

让新知识在旧的知识生长出来，就会十分自然却容易被学生所接受.这是一个很重要的想法，因此教师在教学时，要基于学生“最近发展区”提出问题，要基于学生认知特点和思维规律，教育心理学家奥苏贝尔曾经说过，如果把我的教育理论归结为一句话，“那就是知道学生已经会了什么，在这个基础上进行教学.”因此在定理教学中找准新旧知识固着点.例如，教材中直接让学生任意旋转角度，发现圆具有旋转不变性，这一直接操作忽视了原图形和旋转后的图形、原图形的点和旋转后的点之间对应关系的建立，旋转不变性的概念只有建立两个图形之间的对应关系才能深度理解旋转不变性.因此知识间新旧固着点旋转前后的图形建立对应关系，而图形的对应关系体现在点的对应关系，基于这样视角下，寻找特例等边三角形旋转120°后，在几何画板中能感受到点与点之间的对应和旋转前后图形的不变性，然后从特殊到一般感悟到圆具有旋转不变性.又如，在学习圆心角定理之前，学生已经学习垂径定理，这两个定理非常类似，可以通过类比的方法进行学习，当学生得到“在同圆或等圆中，相等圆心角所对的弧、弦都相等”，让学生类比垂径定理的学习，再次提出问题，用基本量的思想思考各要素之间的关系.教师在学生的“最近发展区”提出问题，让学生思考，然后教师再提出更接近目标的问题，使全体学生都得到思考与思维的发展，让知识自然而合理地生发，学生积极而有效的建构.