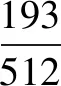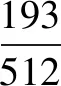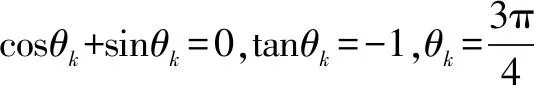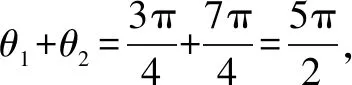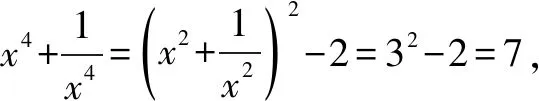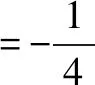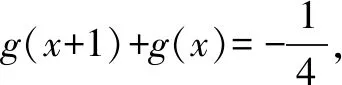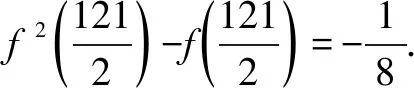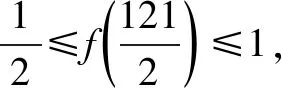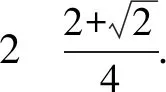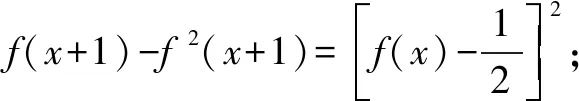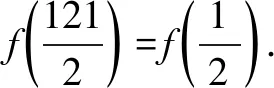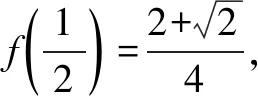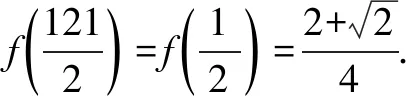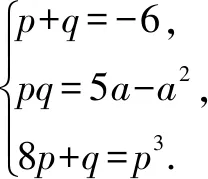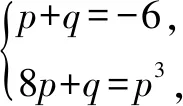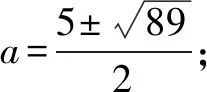2019年浙江大学自主招生数学试题(部分)及其详解

甘志国

(北京市丰台二中 100071)

2019年浙江大学自主招生数学试题有单项选择题、填空题和解答题.本文中的试题均是由参加考试的学生回忆得出的，因而回忆出的题目可能不准确(没有回忆出选项的题目均改成了填空题)，题目也不全，题号也不准确.解得由笔者给出.

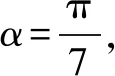
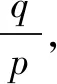
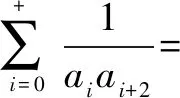
4.若把一枚质地均匀的硬币投掷10次，则正面朝上的次数比正面朝下的次数多的概率是____.

5.现在有一枚质地均匀的硬币，若甲投掷这枚硬币2019次，乙投掷这枚硬币2018次，则在甲投掷的情形中正面朝上的次数比在乙投掷的情形中正面朝上的次数多的概率是____.

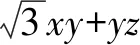
7.已知P(n)是关于n的整系数多项式，若P(0)与P(1)均为奇数，则P(n)( ).

A.无整数根 B.有负整数根

C.有正整数根 D.无实根

9.当n∈N*时，下列说法正确的是( ).

A.若n≠3k(k∈N)，则7|2n-1

B.若n=3k(k∈N)，则7|2n-1

C.若n≠3k(k∈N)，则7|2n+1

B.若n=3k(k∈N)，则7|2n+1

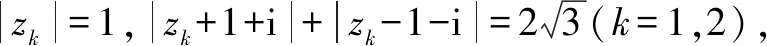
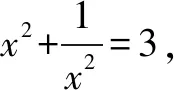
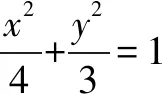
13.若将19表示成若干个正整数之和，则这些正整数之积的最大值是____.

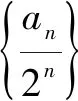
14.若数列{an}的前n项和Sn满足a1=1,Sn+1=4an+3(n∈N*)，则a2019-2a2018=____.

16.若关于x的一元二次方程x2+6x+5a-a2=0的两个实根p,q满足8p+q=p3，则a的取值的个数是____.

17.已知△ABC的两个顶点A,B的坐标分别是(-p,0),(p,0)，且该三角形的内心在直线x=q(0

参考答案

2.7.设x,y∈S，则|x-y|的取值范围是{0,1,2,3}，且|x-y|=0的情形有且仅有4种：x=y=1,2,3,4；

|x-y|=1的情形有且仅有6种：(x,y)=(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)；

|x-y|=2的情形有且仅有4种：(x,y)=(1,3),(3,1),(2,4),(4,2)；

|x-y|=3的情形有且仅有2种：(x,y)=(1,4),(4,1).

可得(a1,a2,a3,a4)的取法共有44=256种.

设α=|a1-a3|,β=|a2-a4|，可得α+β的取值范围是{0,1,2,3,4,5,6}.

(1)当α+β=0即α=β=0时，(a1,a2,a3,a4)的取法共有42=16种；

(2)当α+β=1即(α,β)=(0,1),或(1,0)时，(a1,a2,a3,a4)的取法共有(4·6)·2=48种；

(3)当α+β=2即(α,β)=(0,2),(1,1),或(2,0)时，(a1,a2,a3,a4)的取法共有42+62+42=68种；

(4)当α+β=3即(α,β)=(0,3),(1,2),(2,1),或(3,0)时，(a1,a2,a3,a4)的取法共有(4·2+6·4)·2=64种；

(5)当α+β=4即(α,β)=(1,3),(2,2),或(3,1)时，(a1,a2,a3,a4)的取法共有6·2+4·4+2·6=40种；

(6)当α+β=5即(α,β)=(2,3),或(3,2)时，(a1,a2,a3,a4)的取法共有(4·2)·2=16种；

(7)当α+β=6即α=β=3时，(a1,a2,a3,a4)的取法共有2·2=4种.

所以|a1-a3|+|a2-a4|即α+β的平均数为

进而可得p=2,q=5，所以p+q=7.

3.1.由题设，可用数学归纳法证得an≥n(n∈N)，进而可得

所以

证明如下：

设甲、乙两人在试验中出现正面向上的次数分别是ξ,η，则

因为

所以乙抛掷的硬币中出现正面向上的次数比甲多的概率是

P(η>ξ)=P(η=1且ξ=0)+P(η=2且ξ=0,1)+P(η=3且ξ=0,1,2)+…+P(η=n+1且ξ=0,1,2,…,n)

6.-1.由题设，可得

7.解法1 A.当P(n)=1-3n+n2时，P(0)=1与P(1)=-1均为奇数，由此可排除选项B,C,D.

下面证明选项A正确.可设

P(n)=a0+a1n+a2n2+…+aknk(a0,a1,a2,…,ak∈Z,k∈N).

当k=0时，可得P(n)=a0(a0是奇数)，进而可得选项A正确.

当k∈N*时，由题设可得a0为奇数，a1+a2+…+ak为偶数.

若多项式P(n)有整数根x0，可得

所以x0|a0,x0为奇数.

(1)当a1,a2,…,ak全为偶数时，可得P(x0)为奇数.

(2)当a1,a2,…,ak中有奇数时，可得奇数的个数是偶数，进而可得P(x0)也为奇数.

均得选项A正确.

解法2 A.同解法1知，选项B,C,D均不正确.下面证明选项A正确.

假设P(n)有整数根a，可得P(n)=(n-a)g(n),g(n)是整系数多项式.

所以P(0)=-ag(0),P(1)=(1-a)g(1).因为(1-a)-(-a)=1是奇数，所以1-a,-a这两个整数一奇一偶；另一方面，由P(0)和P(1)都是奇数，可得1-a,-a都是奇数.前后矛盾！所以欲证结论成立.

9.B.当n=1时，7|2n-1及7|2n+1均不正确，所以选项A,C均错误.

当k=0即n=0时，可得选项B正确；当k∈N*时，可得2n-1=23k-1=(1+7)k-1，再由二项式定理可知7|2n-1.总之，可得选项B正确.

由选项B正确，可得选项D错误.

所以

13.972.易知，当这些正整数之积最大时，每个正整数都不会是1.

把每个大于2的正整数x拆成2+(x-2)时，和不变；2(x-2)≤x⟺x≤4.这说明当这些正整数之积最大时，每个正整数都是2,3,4之一.

把4拆成2+2时，积不变：2×2=4.所以当这些正整数之积最大时，每个正整数可以都是2,3之一.

再由2+2+2=3+3,2×2×2<3×3可知，当这些正整数之积最大时，每个正整数都是2,3之一且2的个数是1或2，进而可得把19拆成3+3+3+3+3+2+2时，得到的这些正整数之积最大，且最大值是35×22=972.

14.22019.由题设，可得

Sn+2=4an+1+3,Sn+1=4an+3(n∈N*).

相减，得

an+2=4an+1-4an,an+2-2an+1=2(an+1-2an)(n∈N*),

还可得a2-2a1=6-2·1=4，所以

an+1-2an=4·2n-1=2n+1(n∈N*),

a2019-2a2018=(2019·22019-22018)-2(2018·22018-22017)=22019.

平方，得

[f2(x+1)-f(x+1)]+[f2(x)-f(x)]

由②，

所以

由题设，可得

再由f(x)是R上的偶函数，可得

当(p,q)=(-3,-3)时，由pq=5a-a2，可得a2-5a+9=0，可得此方程无实根.

综上所述，可得所求答案是4.

17.如图1所示，设△ABC的内切圆的圆心为I，该圆与边AB,BC,CA分别切于点D,E,F.

由切线长定理，可得

|CA|-|CB|=|FA|-|EB|=|DA|-|DB|=(q+p)-(p-q)=2q<2p=|AB|.