一种引力搜索优化神经网络的调制识别算法

杨 洁, 吴凤杰

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

在数字通信过程中，正确识别信号的调制方式，可进一步估计信号的相关调制参数，从而正确分析处理信号。随着无线通信环境的日益复杂，自动调制识别已成为电子战、信号检测等领域的重要课题[1]。

目前，自动调制识别通常采用统计模式识别方式，主要包括基于瞬时信息[1]，高阶累积量和小波变换[2]等方法提取的信号特征模块；基于决策树[3]、支持向量机[4]和神经网络[5]等分类器识别模块。

基于瞬时信息提取的特征计算量小且易实现，但是受噪声影响较大，在低信噪比条件下识别率不高，同时反向传播(back propagation, BP)神经网络存在收敛速度慢，容易收敛到局部最优等问题[6]。为了改善信号识别率，引入弹性BP算法提高训练速度[7]；引入蜂群算法提取信号特征，再利用神经网络进行识别[8]；分别利用粒子群算法、遗传算法优化神经网络的权值和阈值，增大获得全局最优解的概率[9-10]。但是，上述方法均存在收敛较慢、未能达到理想结果等问题。

引力搜索算法(gravitational search algorithm, GSA)是一种启发式的优化算法，其收敛性能均优于粒子群算法和遗传算法等算法[11]。但是,引力搜索算法又存在容易局部收敛问题。因此，本文提出一种混合引力搜索算法(hybrid-gravitational search algorithm, HGSA)。利用Tent映射[12]和柯西扰动[13]平衡局部最优和全局最优，并对引力常数进行改进，从而提高引力搜索算法的收敛速度。最后，利用HGSA优化神经网络权值和阈值，将通过基本瞬时特征、高阶累积量特征和小波变换特征提取信号的6个特征参数，输入优化后的神经网络分类器对信号进行分类识别。

1 特征提取

7种常用的待识别信号分别为二进制幅度键控(2-amplitude-shift keying, 2ASK)、4ASK、二进制频移键控(2-frequency-shift keying, 2FSK)、4FSK、二进制相移键控(2-phase-shift keying, 2PSK)、4PSK和十六进制正交幅度(16-quadrature amplitude modulation, 16QAM)。各调制信号的统一表达式[14]为

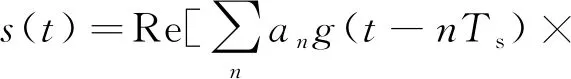
(1)

其中，an为调制码元，g(t)为成形函数，t为时间，Ts为采样间隔，fc和θc分别是载波频率和相位，n为码元个数，θn是调制相位，ω(t)是高斯白噪声。利用基本瞬时特征、高阶累积量特征和小波变换特征，提取的6个特征分别为瞬时幅度均方差之比R；零中心归一化瞬时幅度绝对值的标准偏差σ；4阶累积量之比T1、T2；6阶与4阶累积量之比T3和频率峰值特征T4。

1.1 基本瞬时特征

根据信号瞬时幅度均值的平方与瞬时幅度方差之比[3]

(2)

将含有幅度信息的信号2ASK，4ASK和16QAM分为一类；不含幅度信息的信号2PSK，4PSK，2FSK和4FSK信号分为另一类。其中，u为信号瞬时幅度的均值，d为信号的瞬时幅度方差。

2ASK信号只有两个幅度信息，零均值归一化之后幅度信息归零。因此，根据零中心归一化瞬时幅度绝对值的标准偏差[4]

(3)

可以将2ASK和4ASK分开。Ns为码元序列长度，k∈(1,2,…,Ns)，A为零中心归一化瞬时幅度。

1.2 高阶累积量特征

在高斯随机过程中，当累积量阶数p≥3时，其累积量等于0，此时噪声将不对信号产生影响。因此，利用高阶累积量可提取被噪声污染信号的有效信息。设X(k)为零均值复平稳随机过程，则p阶联合矩[2]可表示为

Mpq=E[X(k)p-qX*(k)q]。

(4)

其中，X*(k)为信号X(k)的共轭，E[·]表示求信号期望，q为共轭位置，且q∈(1,2,…,p)。

4阶累积量与6阶累积量计算量小，且能较好地反映信号的统计特征，故选用其中4个累积量提取信号特征，信号累积量[2]的计算表达式分别为

(5)

C41=M41-3M20M21,

(6)

(7)

(8)

信号的高阶累积量与信号功率密切相关，为消除相关影响，选取|C42|作为归一化标准，将3种累积量比值作为特征参数

T1=|C40|/|C42|,

(9)

T2=|C41|/|C42|,

(10)

T3=|C63|2/|C42|3。

(11)

由式(4)～式(11)可计算出信号2ASK、4ASK、2FSK、4FSK、2PSK、4PSK和16QAM的3个特征参数的理论值，如表1所示。

表1 特征参数的理论值

由表1可以看出，2FSK和4FSK信号的特征参数T1为0，而2PSK和4PSK信号的特征参数T1为1，可将其分为两类。2PSK信号的特征参数T2为1，4PSK信号的特征参数T2为0，可将其分开。2ASK和4ASK信号的特征参数T3大于16QAM信号，可将其分为两类。虽然高阶累积量具有很好的性质，但是其对2FSK和4FSK不能类内识别，故引入小波特征对这一缺陷进行弥补。

1.3 小波变换特征

小波变换[15]是对傅里叶变换进行改进后提出的一种全新的时频分析方法。对于给定平方可积的信号x(t)，其连续小波变换定义为

(12)

其中，ψ(t)为母小波，a为尺度因子，b为时移因子，a，b均为常数，〈·〉表示对信号求内积，“*”表示信号的共轭。

利用式(12)，对信号进行Haar小波变换，并对变换后的瞬时频率进行直方图统计，由此可以得到信号的频率峰值特征T4[15]。当尺度因子a=9时，可获得最大信噪比增益，则各调制信号的T4理论值如表2所示。

表2 参数T4的理论值

由表2可得，2FSK信号的特征参数T4为2，4FSK信号的特征参数T4为4，则可利用此特征将两个频率调制信号区分。

2 HGSA算法优化神经网络

BP神经网络是采用梯度下降法更新权值和阈值从而降低误差的一种单隐层前馈神经网络[16]。由于标准BP算法是根据单个样例进行迭代，在迭代过程中可能会出现不同样例之间相互抵消的情况，又基于梯度下降法原有的缺陷，使得算法可能陷入局部最优。故采用HGSA算法对BP网络参数寻优。

2.1 GSA算法

引力搜索算法中，根据牛顿第二定律，粒子会在力的作用下加速向作用力的方向前进[11]。设在D维搜索空间中存在N个粒子，则第m个粒子的位置为

(13)

在t时刻，第j个粒子作用在第i个粒子上的引力可表示为

(14)

式中，Mj(t)和Mi(t)分别为作用粒子j的惯性质量和被作用粒子i的惯性质量，Ri,j(t)为第i个粒子和第j个粒子之间的欧氏距离，ε为常量，G(t)为t时刻的引力常数，可表示为

(15)

其中，G0为引力常数初始值，T为最大迭代次数，α为引力系数衰减因子。

设其他粒子对第i个粒子的作用力的总和为

(16)

其中rj为第j个粒子取值在[0,1]之间的随机数。

根据牛顿第二定律，第i个粒子在某一时刻的加速度为

(17)

利用适应度值更新惯性质量，则第i个粒子惯性质量更新为

(18)

(19)

其中，fi(t)表示t时刻第i个粒子的适应度值，bf(t)为t时刻全局最小适应度值，wf(t)为t时刻全局最大适应度值。

由式(13)至式(19)可得第i个粒子在迭代过程中位置和速度的更新公式分别为

(20)

(21)

其中ri为第i个粒子取值在[0,1]之间的随机数。

2.2 HGSA算法

GSA算法虽然收敛较快但是全局收敛性较差，容易陷入局部收敛。HGSA算法通过引入Tent映射初始化种群，利用柯西扰动避免早熟，以及自适应的改变引力常数，从而改善GSA算法的缺陷。

2.2.1 基于Tent映射的种群初始化

利用混沌优化算法中Tent映射产生初始种群，所得到的序列不仅服从均匀分布，且对于不同参数具有近似一致的分布密度[12]。种群粒子初始位置的Tent映射表达式为

(22)

其中，N为种群内粒子总个数，r是小于1的随机实数，xi为种群中第i个粒子，i∈(1,2,…,N)。利用式(22)得到的粒子，降低了种群初始化对算法优化的影响，使其具有更好的遍历性和随机性，降低陷入局部最优的风险，增加全局搜索的能力。

2.2.2 精英粒子柯西扰动

在种群更新过程中，全局最优粒子影响粒子更新的效果，一旦最优粒子陷入局部收敛，将对最终结果产生负面影响，对精英粒子进行轻微扰动则可使其跳出局部最优[13]。选取最优粒子的前10%作为精英粒子。随机变量x的柯西标准分布函数记为x～C(0,1)，其分布函数表达式[13]为

(23)

则精英粒子在迭代过程中位置的柯西扰动可表示为

(24)

2.2.3 改进引力常数

在引力搜索算法中，引力常数G直接影响粒子加速度的大小，从而影响整个算法的收敛速度。参数α是最为重要的一环，当α取值较小时，粒子加速度较大，有助于全局收敛；当α取值较大时，则会加快收敛速度，有助于局部收敛[17]。通过增加迭代次数，自适应改变衰减因子

(25)

其中γ,η为自适应因子常数。式(25)表明在迭代开始时α较小，随着迭代次数的增加α随之变大，从而改善了算法的收敛性能。

2.3 优化神经网络

HGSA算法优化BP神经网络，主要就是利用Tent映射产生初始化的神经网络权值和阈值，然后根据神经网络输出误差，利用式(25)改进的引力常数更新式(21)，以及利用式(23)使神经网络跳出局部最优。最后通过HGSA算法不断迭代优化神经网络，最后得到神经网络的最优阈值和权值。

HGSA优化神经网络的识别算法步骤如下。

步骤1根据式(1)-(12)，对2ASK、4ASK、2FSK、4FSK、2PSK、4PSK和16QAM等7种信号提取R、σ、T1、T2、T3和T4等6个特征参数。

步骤2确定神经网络的拓扑结构，根据式(22)映射初始化神经网络的权值和阈值，确定引力常数、种群大小和最大迭代次数等参数。

步骤3利用神经网络进行训练，计算各粒子的适应度值，找出最优粒子和精英粒子。

步骤4判断最优粒子是否变化，若存在变化则转到步骤5，否则判断变化总次数是否大于阈值，若小于阈值则转到步骤5，否则对精英粒子柯西扰动。

步骤5根据式(15)和式(25)更新引力常数，式(19)更新粒子质量，式(17)更新粒子加速度，式(20)和式(21)更新粒子速度和粒子位置。

步骤6若迭代次数已达到最大，则转到步骤7，否则转到步骤3，重新迭代。

步骤7得到神经网络的最优阈值和权值，将提取信号的6个特征参数，输入优化后的神经网络分类器对信号进行分类识别。

3 仿真实验与结果分析

利用Matlab 2016a软件进行仿真验证。仿真参数设置为载波频率fc=150 kHz，采样频率fs=1 200 kHz，码元速率fd=12.5 kb/s，信号长度取100个码元，选用加性高斯白噪声信道条件。选取R，σ，T1，T2，T3和T4等6个特征参数样本，输入神经网络对2ASK，4ASK，2FSK，4FSK，2PSK，4PSK和16QAM等7种信号进行分类。

HGSA优化BP神经网络算法的参数设置为最大迭代次数为50；种群规模选取40；引力常数G0=100，自适应因子γ=10，η=0.1；柯西扰动因子λ=0.1。训练最大次数为100，目标误差为10-4，学习率为0.1，网络结构有6个输入节点，10个隐含层节点数，7个输出节点，网络采用BP网络进行训练，隐层和输出层均选用sigmoid作为激活函数。

3.1 特征参数随信噪比变化情况

在信噪比(signal noise ratio, SNR)1～20 dB区间内，取信噪比变化步长为1 dB，在同一信噪比条件下，将2ASK、4ASK、2FSK、4FSK、2PSK、4PSK和16QAM等7种信号分别独立仿真200次，取其平均值，得到7个信号的不同特征参数随SNR变化的仿真分别如图1-图6所示。

图1 R随SNR的变化曲线

图2 σ随SNR的变化曲线

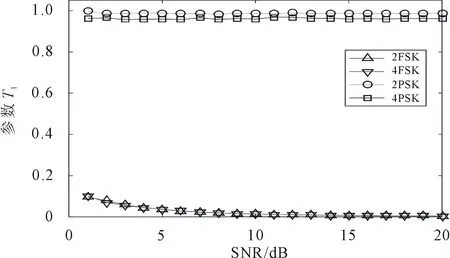
图3 T1随SNR的变化曲线

图4 T2随SNR的变化曲线

图5 T3随SNR的变化曲线

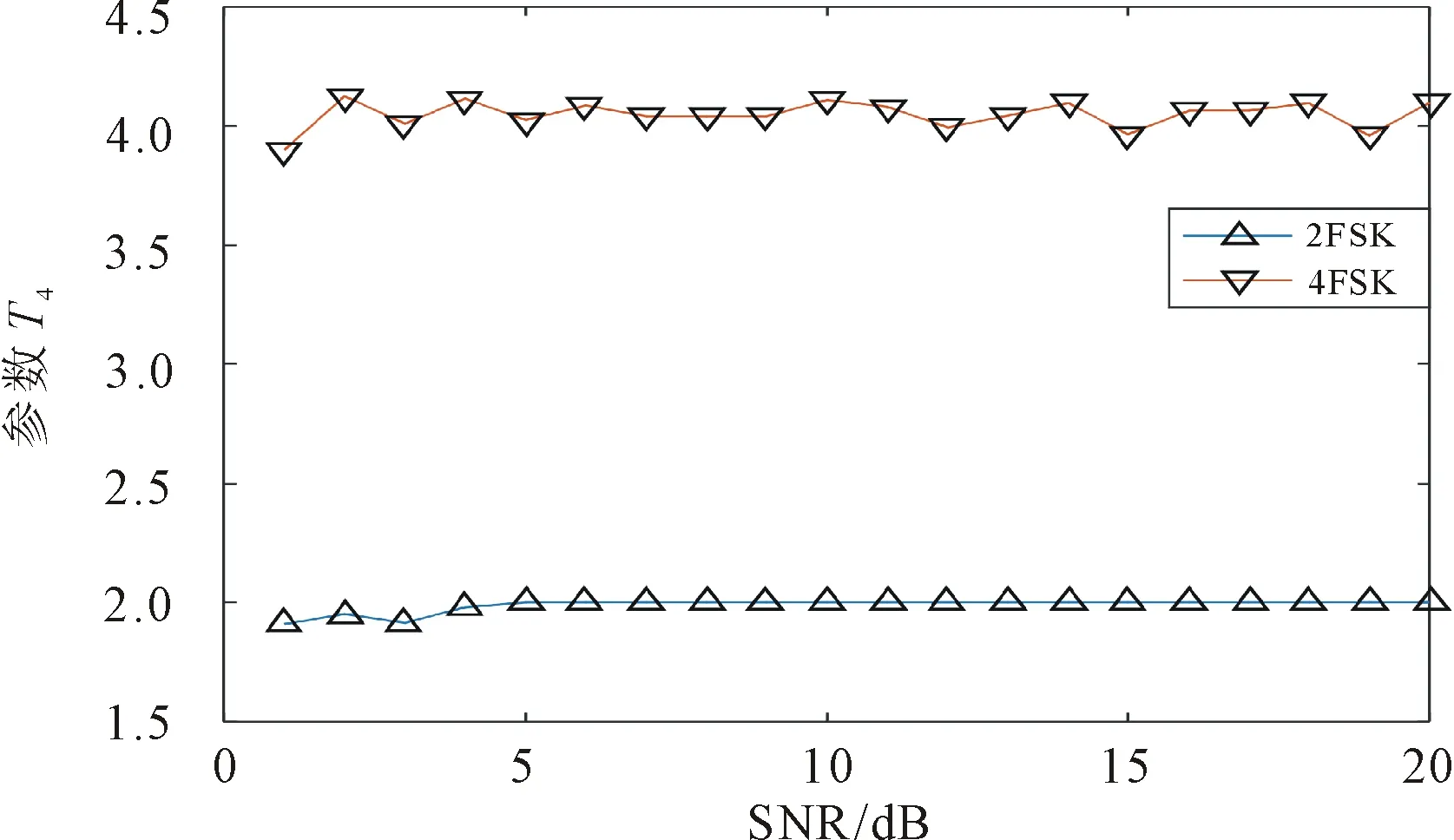
图6 T4随SNR的变化曲线

由图1可以看出，随着信噪比不断加大，瞬时幅度信息的区别不断变大，可以有效地分辨出含有幅度信息和不含有幅度信息的信号；图2表明，即使在低信噪比情况下，两种信号都具有明显的区分度，可以有效地区分；图3-5表明，仿真结果符合高阶累积量的理论值，区分度明显，可以有效识别多种信号；图6表明，在不同信噪比条件下，2FSK和4FSK的特征无多大变化，说明小波变换提取的特征具有良好的抗噪性，且信号区分度明显。

3.2 引力常数有效性验证

选取基准测试函数Rosenbrock[15]，分别利用GSA算法和HGSA算法对基准函数进行寻优迭代，从而验证改进引力常数的有效性。设置迭代次数为200，分别独立运行10次取平均值作为最终结果，得到函数最优适应度值随迭代次数的变化曲线，如图7所示。

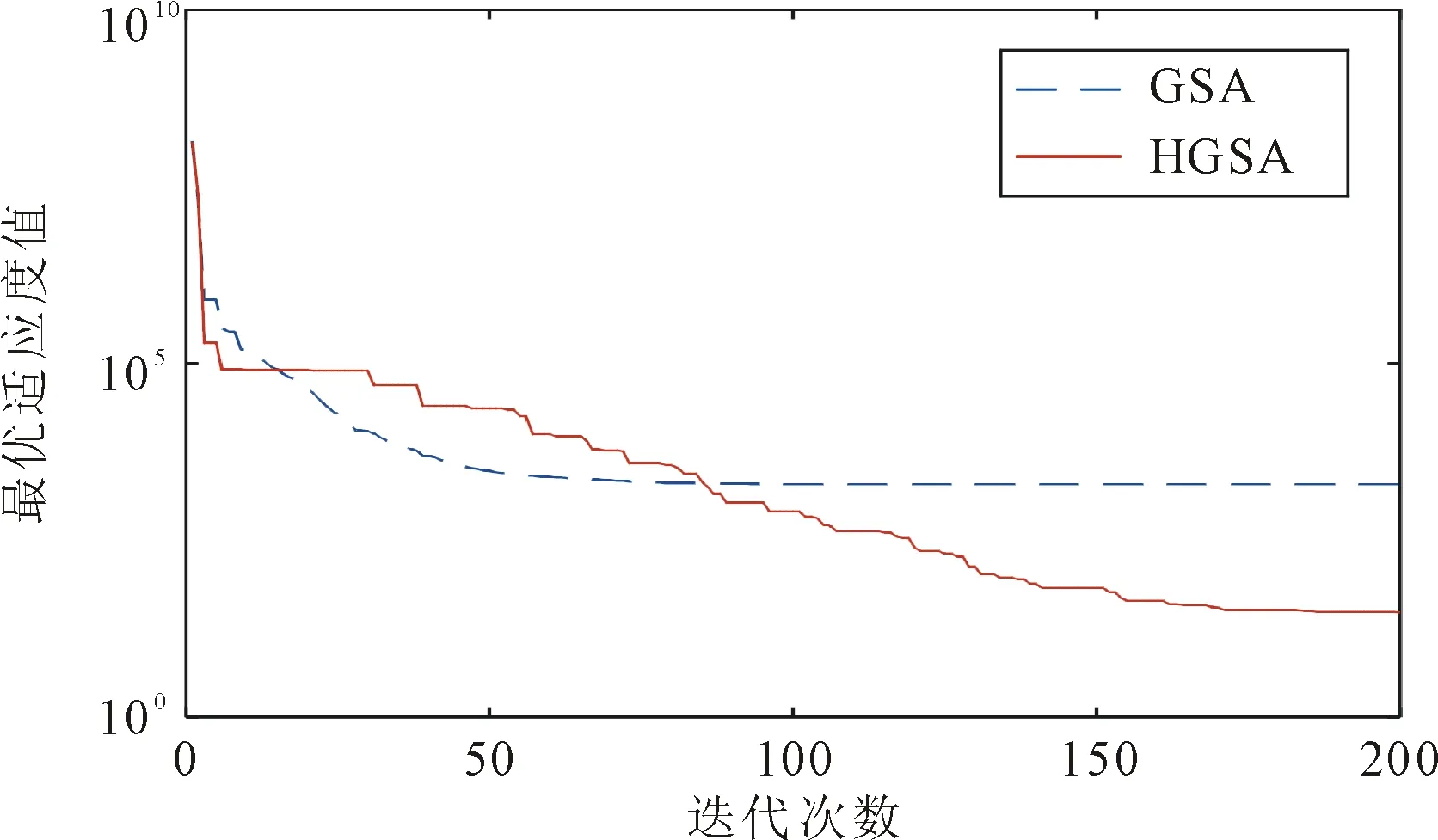
图7 两种算法对函数寻优过程曲线

从图7可以看出，HGSA寻优收敛速度优于GSA算法。在迭代200次后，HGSA最终结果为30.227，而GSA算法的最终结果为1 936.88，HGSA算法相比于GSA算法最终结果低于两个量级，其在迭代过程中可以很好的跳出局部最优，充分说明改进算法的可行性和优越性。

3.3 算法性能比较

在信噪比-5～10dB区间内，选取信噪比1 dB为更新步长，在单个信噪比条件下每个调制信号分别产生50组样本参数，作为训练样本输入神经网络。不断迭代至最大次数，选取每次迭代的最优值作为输出，分别进行10次实验，取平均值作为最终结果。另外分别在不同信噪比下产生100组信号特征，作为测试样本，利用训练后的神经网络进行识别，训练和测试分别进行10次实验，即每类调制信号仿真100×10次，取平均值得到最终仿真结果。对比GSA算法优化BP网络算法(GSA-BP)和HGSA算法优化BP网络算法(HGSA-BP)性能，以及不同信噪比条件下的平均识别率，结果分别如图8和图9所示。

由图8可以看出，GSA-BP算法在粒子迭代到第12代时就已经陷入局部最优，而HGSA-BP算法在粒子陷入局部最优时会经过迭代从而跳出局部最优，继续寻找最优值。在达到最大次数后，GSA-BP算法最优适应度值为0.039 5，而HGSA-BP算法最优适应度值达到了0.038 4，提高较大。相比GSA-BP算法，HGSA-BP算法的复杂度也并没有增加太大，搜索精度的提高完全可以补偿由此带来的搜索速度的增加。

从图9可以看出，HGSA-BP算法比GSA-BP算法更好的识别效果，并且在低信噪比条件下识别率提高7%，更能体现出算法的优越性。

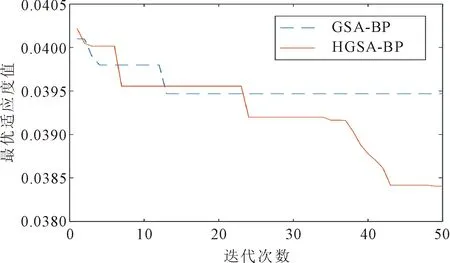
图8 两种算法的最优适应度值变化曲线

图9 两种算法的信号平均识别变化曲线

3.4 不同信号识别率仿真

在信噪比-5～10 dB区间内，选取信噪比2 dB为更新步长，通过HGSA-BP算法识别2ASK、4ASK、2FSK、4FSK、2PSK、4PSK和16QAM等7个信号，信号识别率如表3所示。

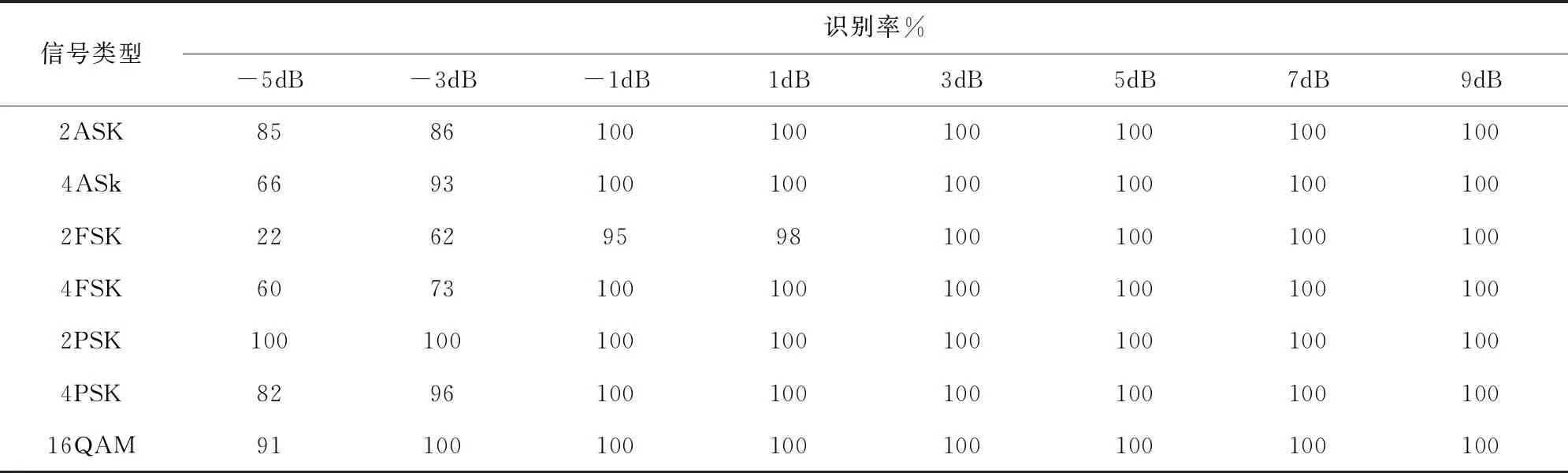
表3 7种调制信号的识别率

由表3可以看出，在3 dB时，7种调制信号就已经全部识别成功，识别率达到100%。在低信噪比时，2FSK和4FSK识别率相比于其他信号识别率不高，但随着信噪比的增加识别率也随之增加，在信噪比为-1 dB时已达到95%以上。

粒子群优化小波神经网络[6]对信号进行识别时，在信噪比为1 dB时，信号识别率到达90%以上；基于改进粒子群优化BP神经网络[9]对信号进行识别时，当信噪比大于等于10 dB时，信号识别率达到94%；而HGSA-BP算法在信噪比为-1 dB时，信号识别率已到达95%以上，且算法复杂度较低。

4 结语

基于HGSA算法优化神经网络的调制识别算法，通过瞬时特征，高阶累积量和小波变换提取的6个特征参数，降低了噪声对信号特征的干扰，且特征明显，具有较大的区分度。利用Tent映射初始化种群平衡了局部最优和全局最优，自适应改变引力衰减因子提高了收敛速度，利用柯西扰动降低了BP神经网络陷入局部最优的可能性，得到了最优适应度值，并且在低信噪比条件下具有较高的识别率，实现了2ASK，4ASK，2FSK，4FSK，2PSK，4PSK，16QAM等7种基本调制信号的自动识别。仿真结果表明，HGSA算法在寻优速度和寻优效果上均明显优于GSA算法，且在信噪比为-1 dB时，信号的整体识别率达到95%以上。