激光雷达中扫描振镜控制研究

任福汉,余红英,刘 琛

(1.中北大学，太原 030051； 2.中国电子信息产业集团第六研究所，北京 100083)

0 引 言

激光雷达是探测目标、远程测距、面阵成像常用系统之一，在军事、航天、民用等多领域发挥着巨大作用。在激光雷达系统中，扫描振镜至关重要[1]。扫描振镜(GS)，也称电流计扫描仪，是一种性能优良的矢量扫描器件，是高频驱动下的一种特殊的摆动伺服电机。扫描振镜将激光雷达发射的激光源，通过电机上两个反射镜的摆动，形成激光面阵，达到激光扫描成像效果[2]。

对于扫描振镜的周期性运动控制，传统PID参数整定更多依靠经验，抗干扰能力不足，控制性能无法满足扫描振镜需求。模糊控制是先进控制理论之一，在非线性和时变系统中有较好控制性能，但是模糊控制缺少积分环节，无法消除稳态误差[3]。模糊控制更多是与其他先进控制理论结合，提高控制性能。滑模变结构控制有良好的抗干扰能力、动静态特性，但是存在抖振现象，限制了滑模变结构控制在实际中的应用[4]。基于此，本文提出模糊滑模变结构控制，利用模糊算法抑制滑模变结构控制的抖振现象，提高扫描振镜抗干扰能力。

1 振镜数学模型

扫描振镜在相对较大的角度范围内具有高线性、低惯性的特点，这使得它们可以在高达几千赫兹的扫描频率下使用。为了通过帧扫描获得均匀的光场，帧扫描的频率应该是几十赫兹。激光雷达扫描振镜系统框图如图1所示。

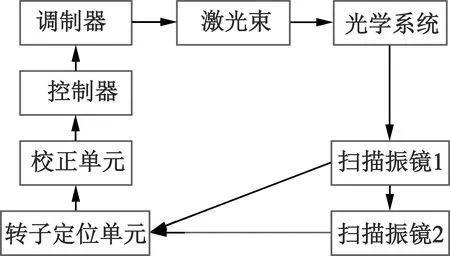
图1 激光雷达扫描振镜系统框图

扫描振镜由电气系统和机械系统组成，扫描振镜电气机械系统组合如图2所示[5]。

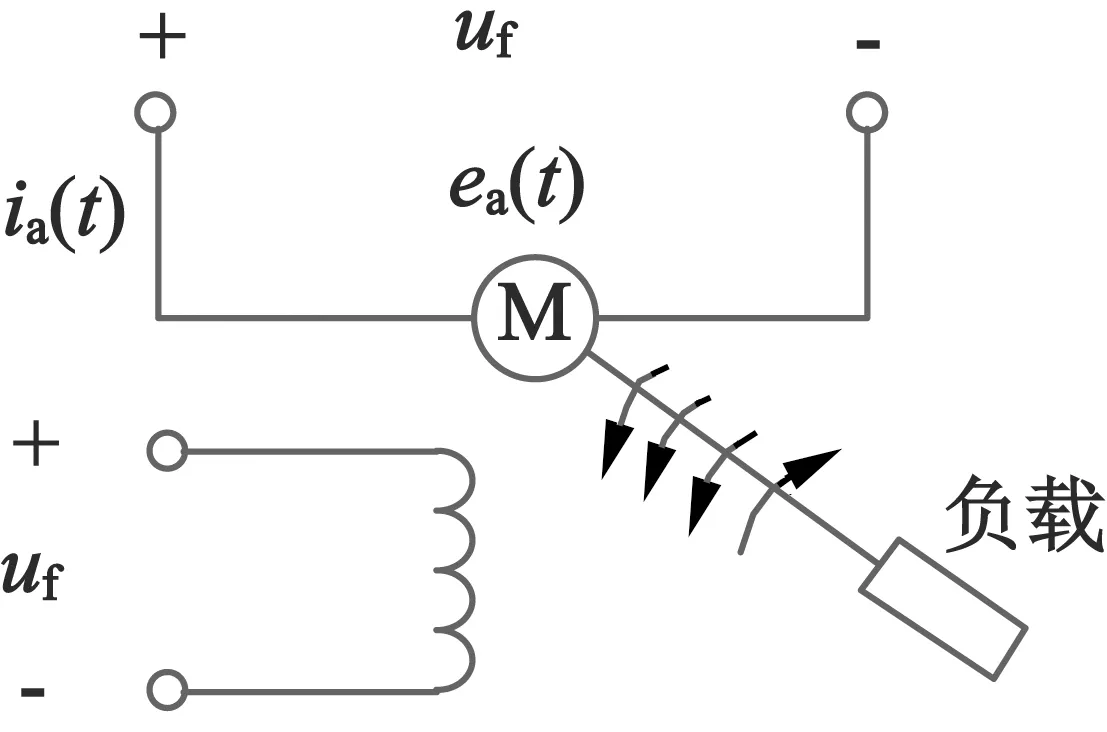
图2 扫描振镜电气机械系统组合

电枢回路微分方程如下：

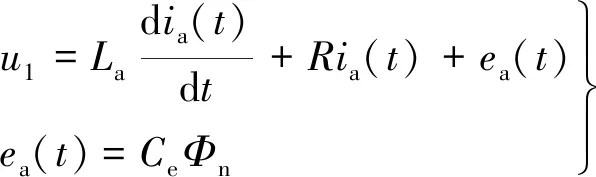
(1)

扫描振镜动力学方程如下：

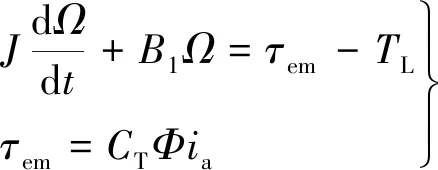
(2)

式中：Ω为机械角速度，Ω=2πn/60。

设系统初始状态为零，对式(1)、式(2)进行拉普拉斯变换，结果如下：

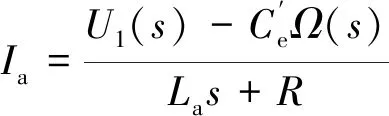
(3)

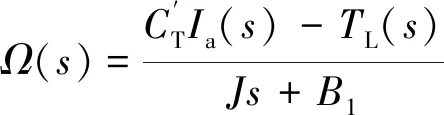
(4)

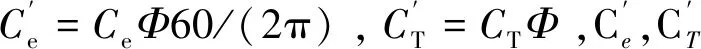
(5)

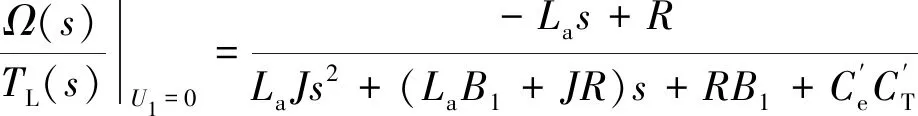
(6)

由式(5)、式(6)扫描振镜传递函数框图如图3所示。

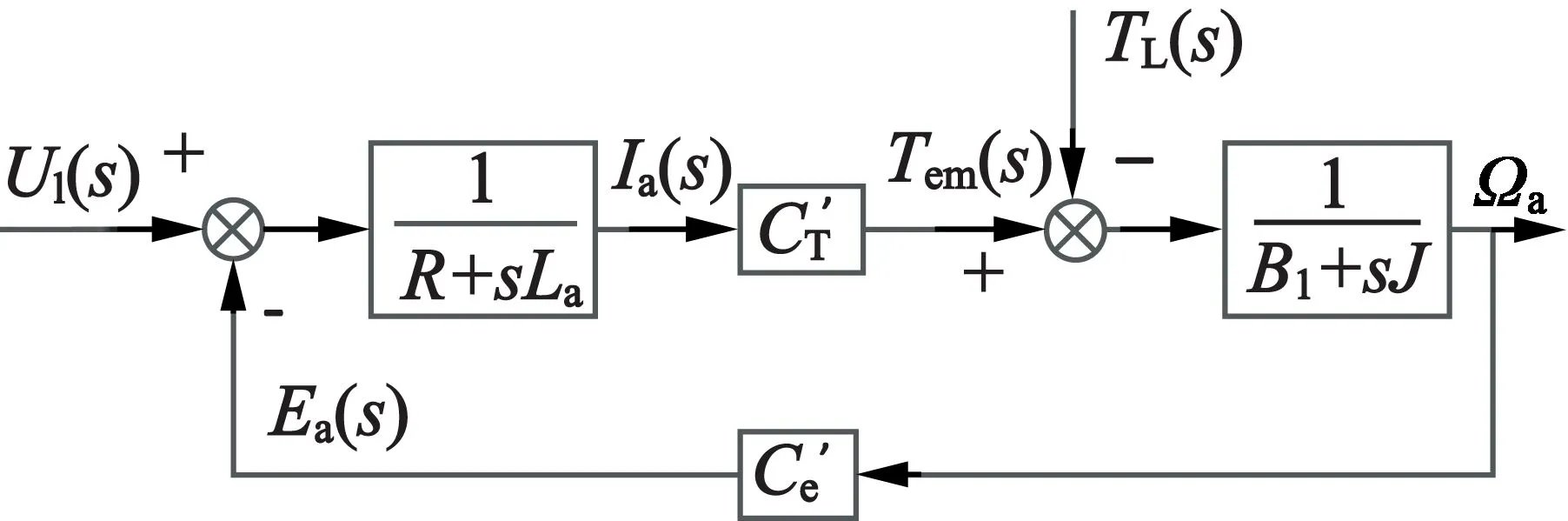
图3 扫描振镜传递函数框图

2 扫描振镜控制算法

2.1 模糊PID控制

完整的模糊控制器包括模糊化接口、推理机(包括数据库和规则库)以及解模糊接口[6]。模糊化接口负责将输入参数模糊化处理，并移交推理机进行规则运算，推理机输出参数通过解模糊接口，计算出系统整定所需参数。

模糊PID控制原理图如图4所示。模糊PID与传统PID相比，在动态响应、静态响应以及鲁棒性方面都有一定的提高[7]，是现代先进控制理论使用较为广泛的控制算法之一。在本文中，模糊PID通过对扫描振镜位置反馈误差e以及误差变化率ec进行模糊化，根据模糊规则实时整定系统控制所需参数KP，KI，KD，以达到期望的控制性能。

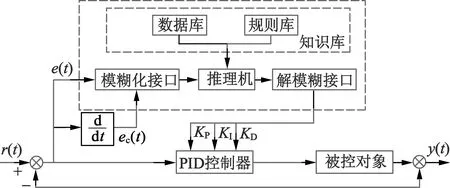
图4 模糊PID控制原理图

输入参数e，ec和输出参数ΔKP，ΔKI，ΔKD模糊子集{NB,NM,NS,NZ,Z,PS,PM,PB}。

设定e，ec是高斯型隶属函数，ΔKP，ΔKI，ΔKD的隶属函数为三角，论域为[-3,3]，得到如表1、表2、表3中对应的ΔKP，ΔKI，ΔKD模糊控制规则表。

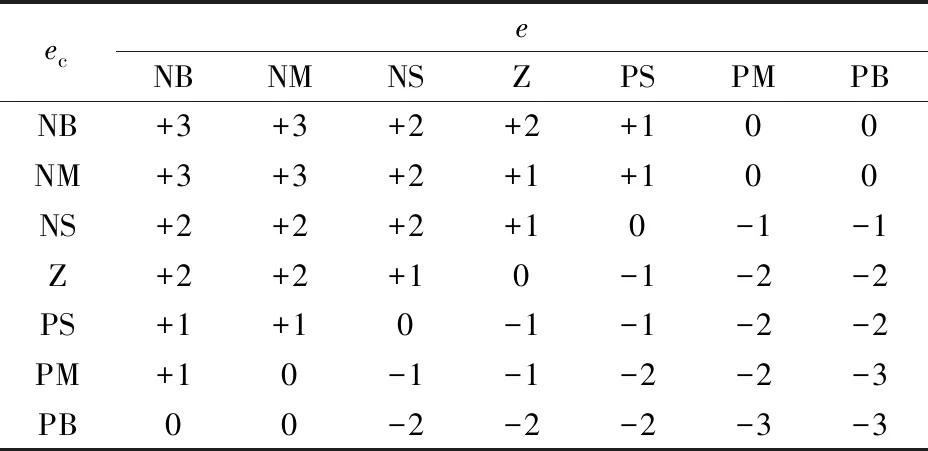
表1 ΔKP模糊规则表

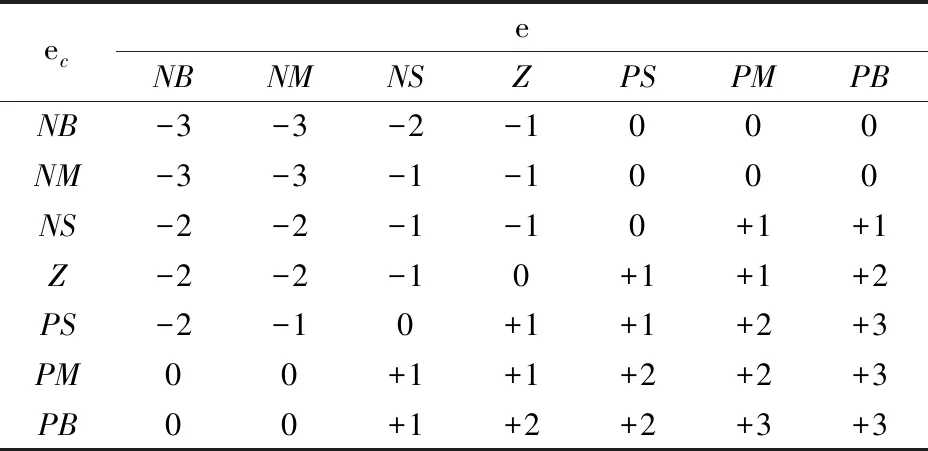
表2 ΔKI模糊规则表

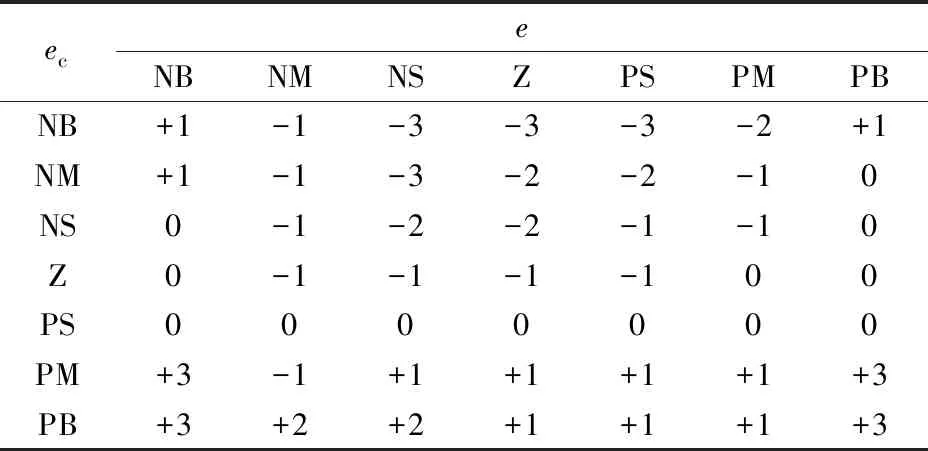
表3 ΔKD模糊规则表

2.2 滑模变结构控制

滑模变结构控制也是先进控制技术之一，是一种变结构控制策略。滑模变结构控制与其他先进控制技术的本质区别在于其非连续控制。滑模变结构控制具有优良的抗干扰能力，但由于存在抖振现象，滑模变结构控制并不能单独应用于实际工程[8]。现对滑模变结构控制进行简要说明。

在欠驱动的滑模变控制系统中，状态表达式：

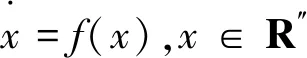
(7)

存在翻转方程s(x)=s(x1,x2,…,xn)=0，状态空间被s(x)划分为s>0及s<0两部分。图5为系统状态空间示意图，图中点A，B，C为状态空间中三种类型，即：通常点A、起始点B以及结束点C。

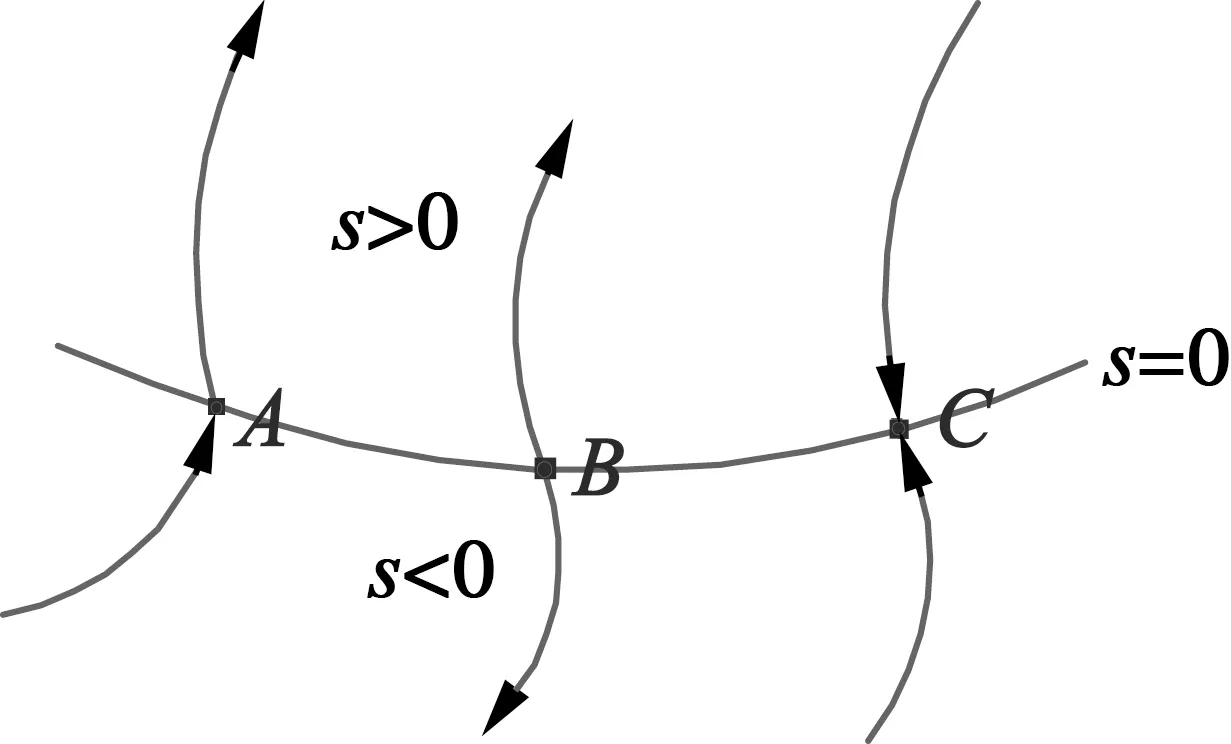
图5 系统状态空间示意图

状态空间中运动点在s(x)=0处是结束点条件：

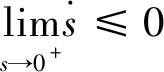
(8)

式(8)也可以表示：

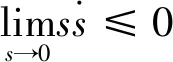
(9)

式(9)对系统提出了一个形如：

v(x1,x2,…,xn)=[s(x1,x2,…,xn)]2

(10)

的Lyapunov约束函数的条件方程。由于在翻转面数值域内，式(10)是正定的，并根据式(9)，s2导数为半负定，在s=0附近v是一个非增函数。所以在式(9)成立的基础上，式(10)为系统条件Lyapunov函数，即系统稳定于s=0。

设控制系统：

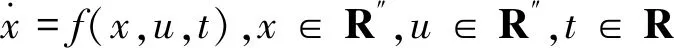
(11)

需要确定其切换函数s(x)，且s∈R″。

求解控制函数：

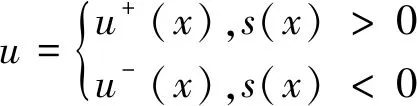
(12)

在本文中，设激光雷达扫描振镜PSD(光位置传感器)位置状态方程：

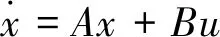
(13)

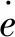
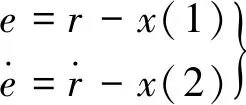
(14)

则切换函数：

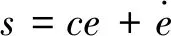
(15)

所以，控制律：

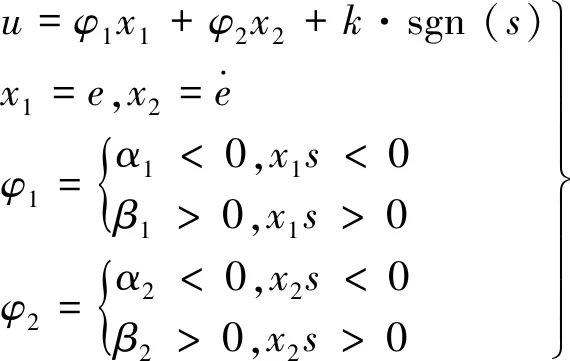
(16)

2.3 模糊滑模变结构控制

建立扫描振镜数学模型时，实际应用环境中诸多影响因素是不可估计的，在应用中会受到较大干扰，但滑模变结构控制需要较大的切换增益，不可避免地产生抖振现象，限制了其在扫描振镜中的应用。根据常规趋近律调节系统参数的方法，能够抑制抖振现象。被调参数需要根据系统条件而定，常规调节方法将被调参数设为恒定值，导致其不能在线调整。为了改进此缺点，更好抑制抖振现象，本文将模糊控制与滑模变结构控制相结合，在滑模变结构控制基础上，引入对切换函数幅值的模糊控制。在模糊控制中，输入为切换函数目前幅值，并根据切换函数幅值计算出模糊控制器输出量，保证系统良好的鲁棒性、抗干扰性，并且最大限度抑制抖振现象。模糊滑模变结构控制原理图如图6所示[9]。

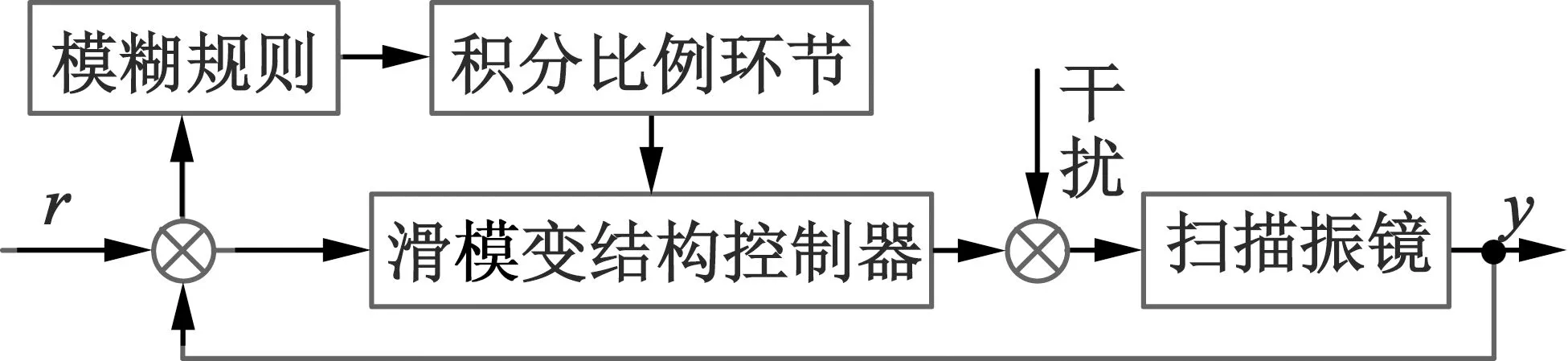
图6 滑模变结构控制原理图

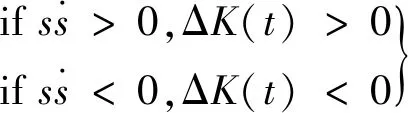
(17)

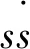
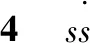
表与ΔK(t)之间模糊规则表

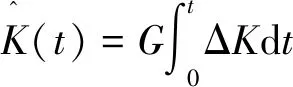
(18)

式中：G是由经验确定的比例系数。则控制率：

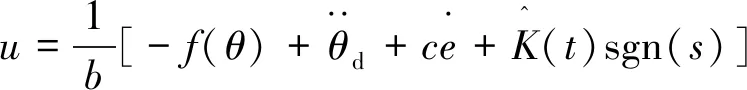
(19)

3 扫描振镜仿真

3.1 模糊PID仿真

在MATLAB中运行Fuzzy Logic Designer，将表1、表2、表3模糊控制规则输入到Ruler Editor，得到ΔKP，ΔKI，ΔKD模糊规则曲面图，如图7所示。

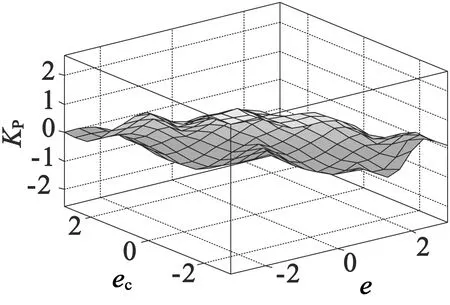
(a) ΔKP

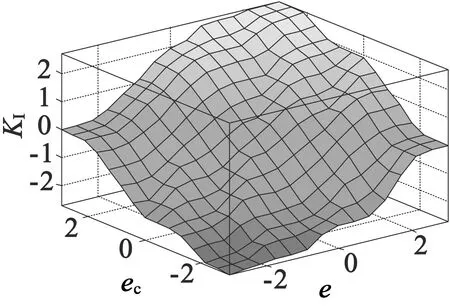
(b) ΔKI

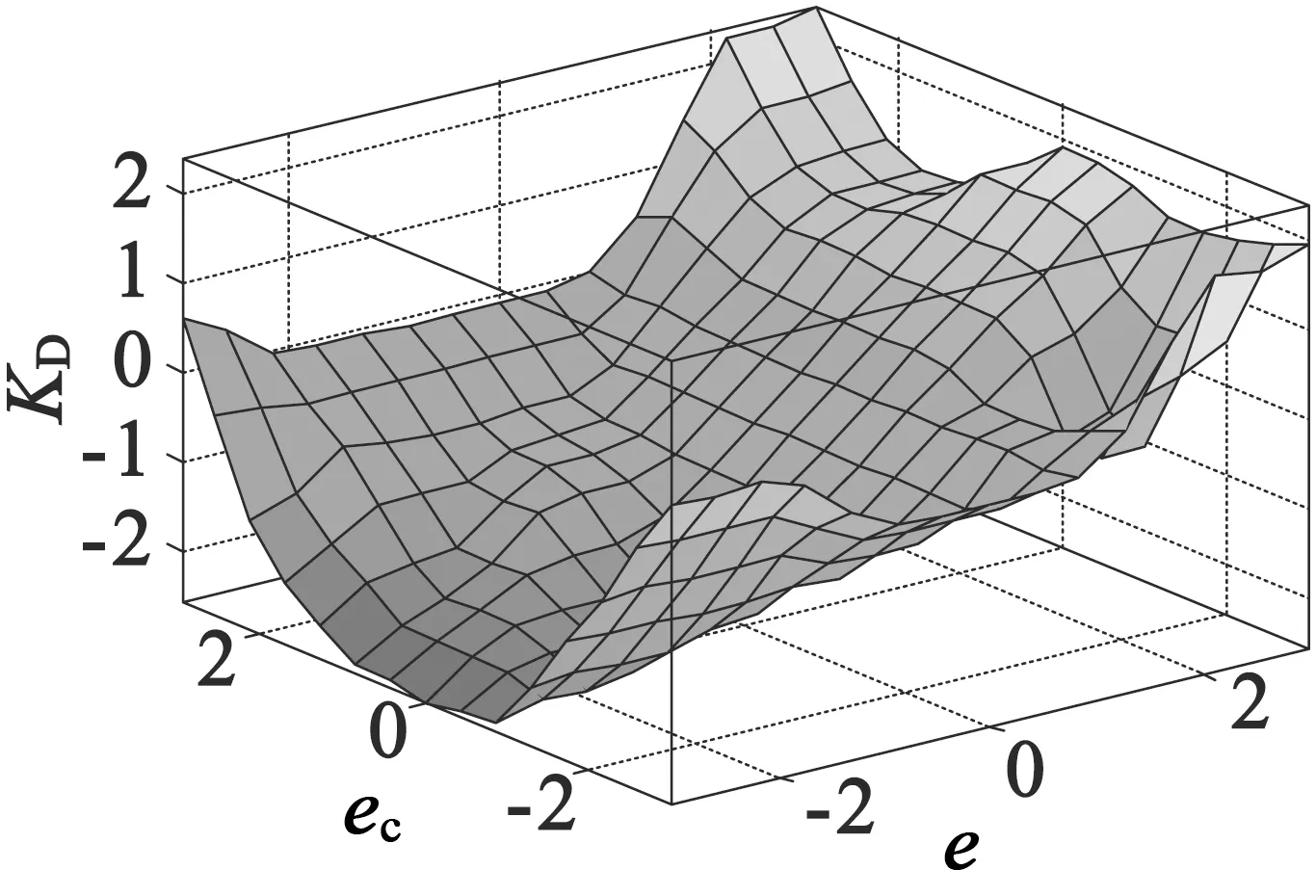
(c) ΔKD图7 ΔKP，ΔKI，ΔKD模糊规则曲面

在Simulink中对PSD数据进行模糊PID控制仿真，其单位阶跃响应曲线、位置误差e、速度ec曲线如图8所示，系统调节时间为3 s，超调量为1%。

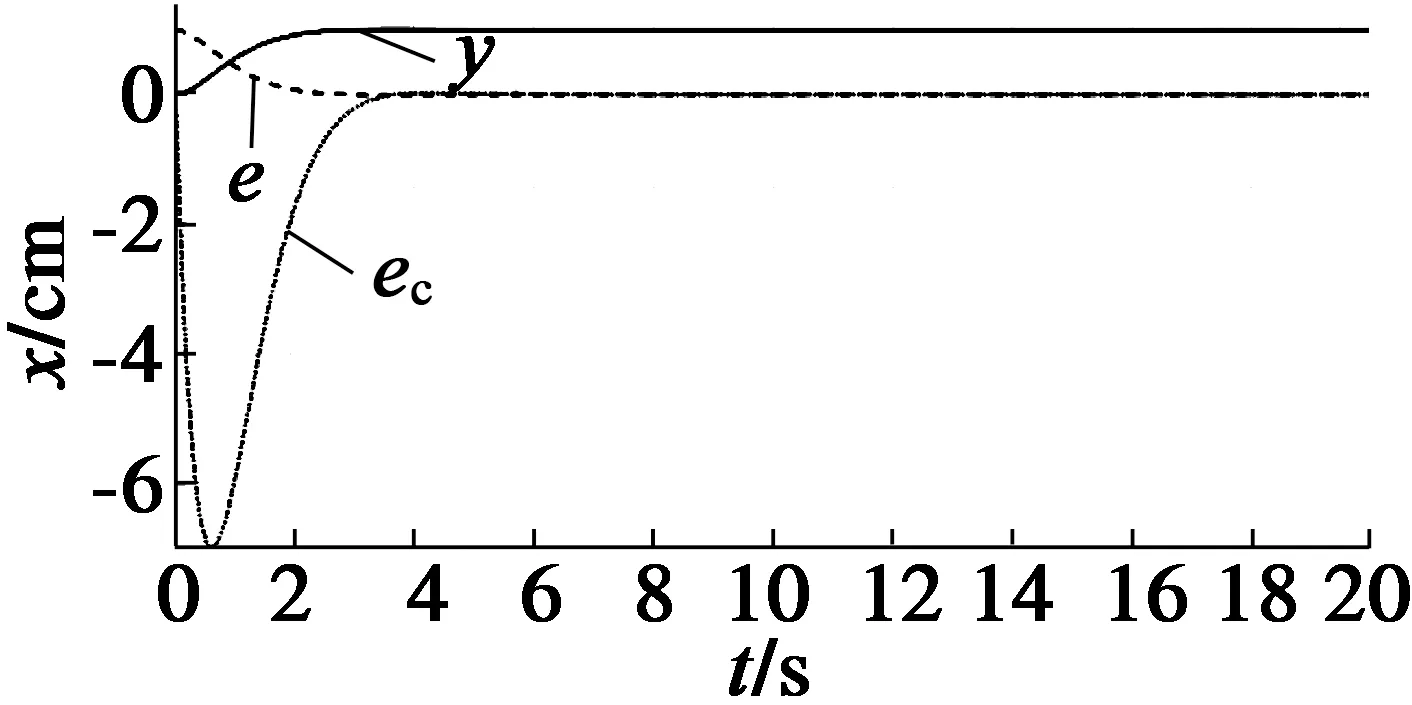
图8 模糊PID仿真曲线

图9是传统PID控制与模糊PID控制脉冲扰动响应曲线。相同情况下加入扰动，模糊PID扰动超调量为18%，传统PID为21%。

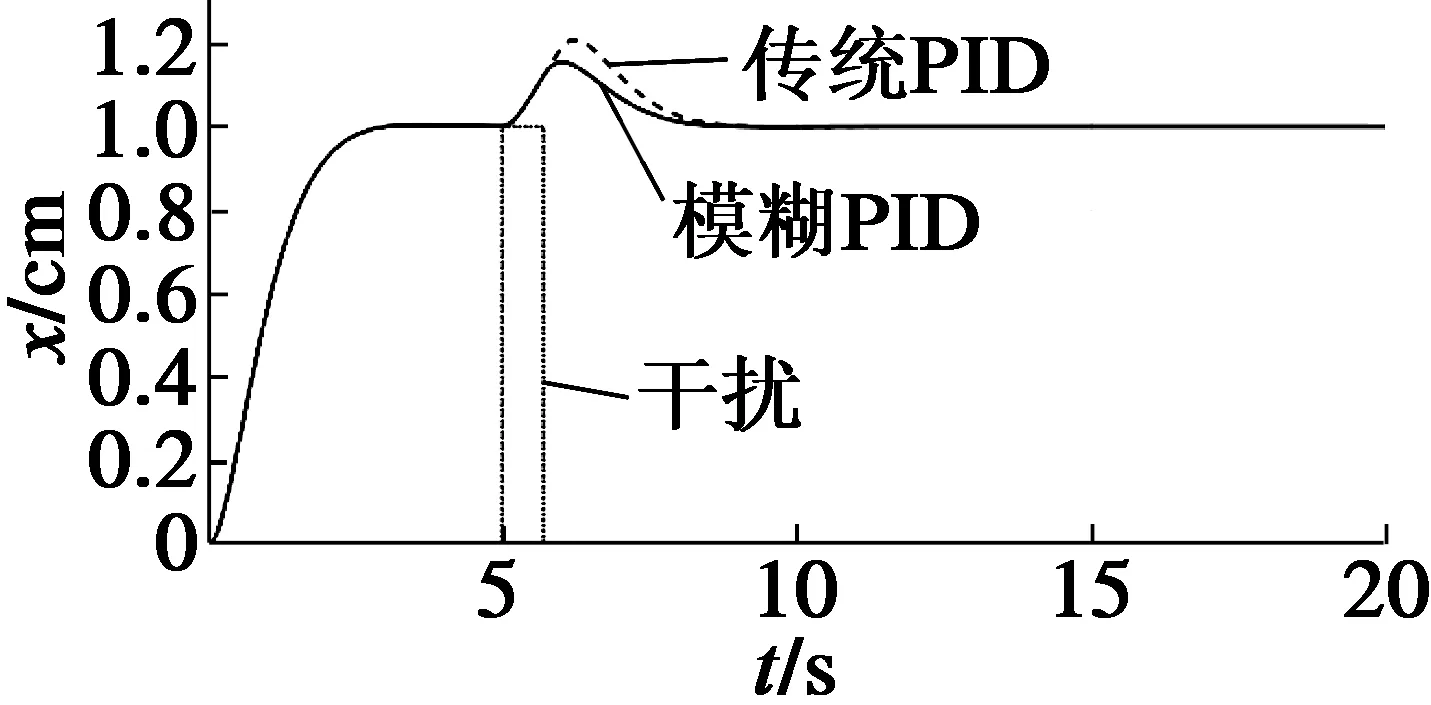
图9 脉冲扰动响应曲线

3.2 滑模变结构仿真

在Simulink中对采用滑模变结构控制的扫描振镜PSD位置环进行仿真，得到PSD数据阶跃响应y、位置误差e、速度误差ec曲线，如图10所示。系统调节时间为3 s，超调量为0.06%。但在y平稳后，存在抖振现象，位置误差e、速度误差ec有明显波动。

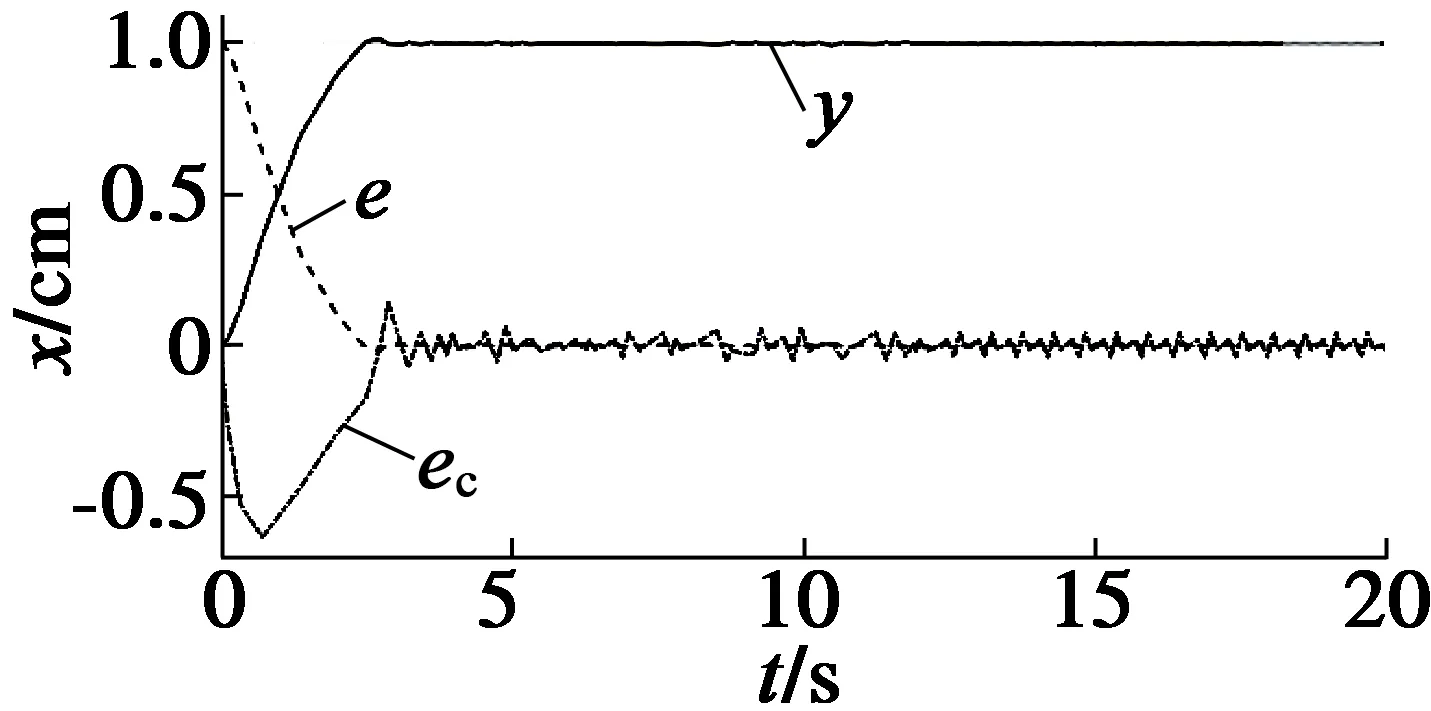
图10 滑模变结构仿真曲线

图11为滑模变结构扰动响应仿真曲线。增加扰动后，系统能够快速恢复，扰动超调量为5.8%，其动态响应和抗干扰能力相比传统PID控制和模糊PID控制有明显提升。但是抖振现象始终存在，不利于系统稳定，违背了激光雷达扫描成像的准确性原则。

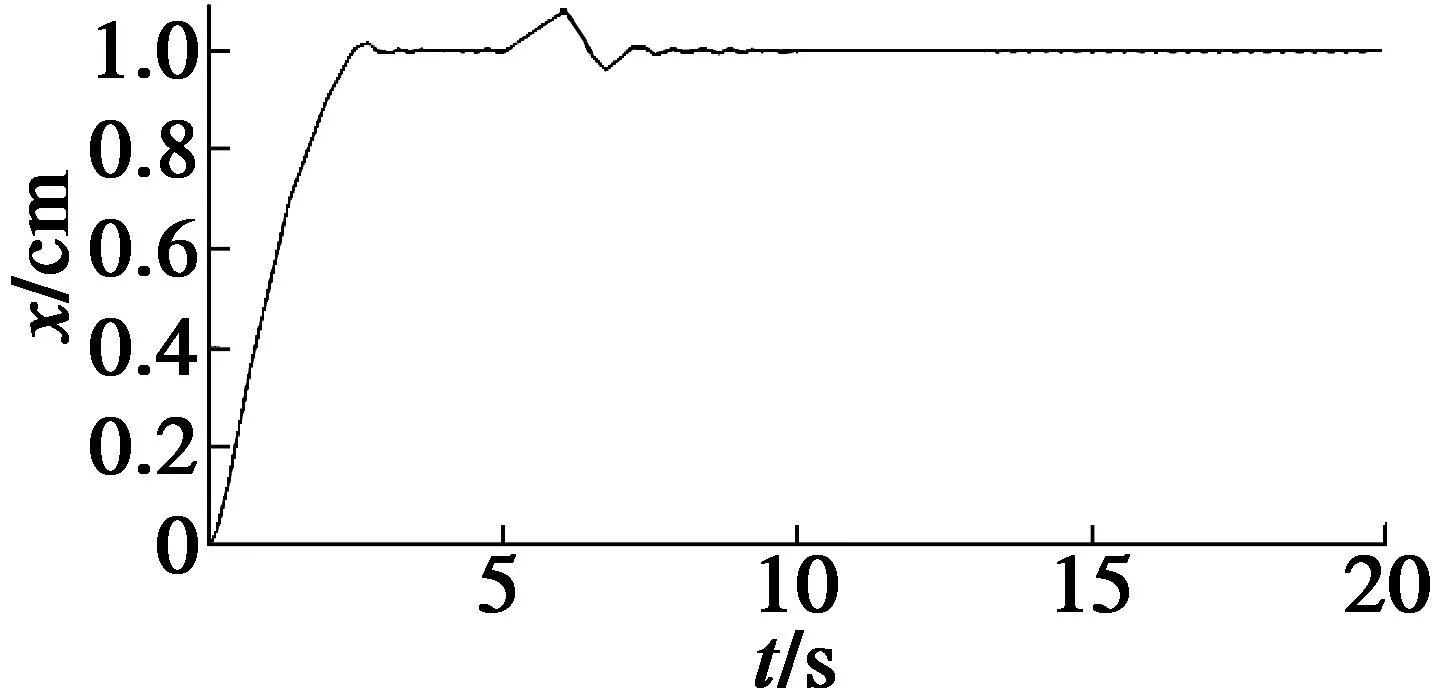
图11 滑模变结构扰动响应曲线

3.3 模糊滑模变结构仿真

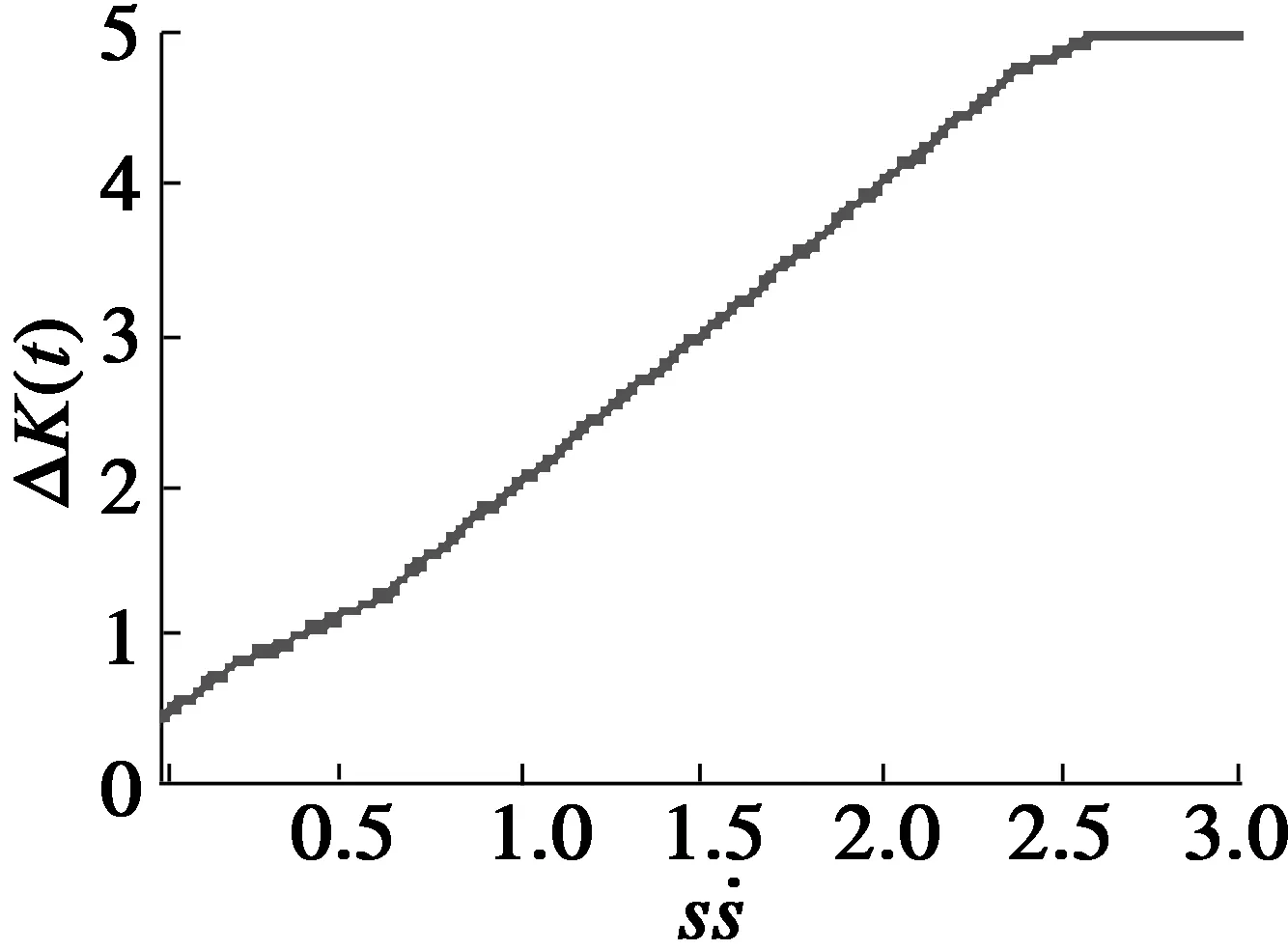
图12 模糊规则曲线

在Simulink中对扫描振镜位置环进行仿真，响应曲线y、位置误差e、速度误差ec如图13所示。与图10相比，模糊滑模变结构控制算法有效抑制了滑模控制系统带来的抖振现象，且控制效果优异，证明本文的模糊滑模变结构控制适用于激光雷达扫描振镜系统。

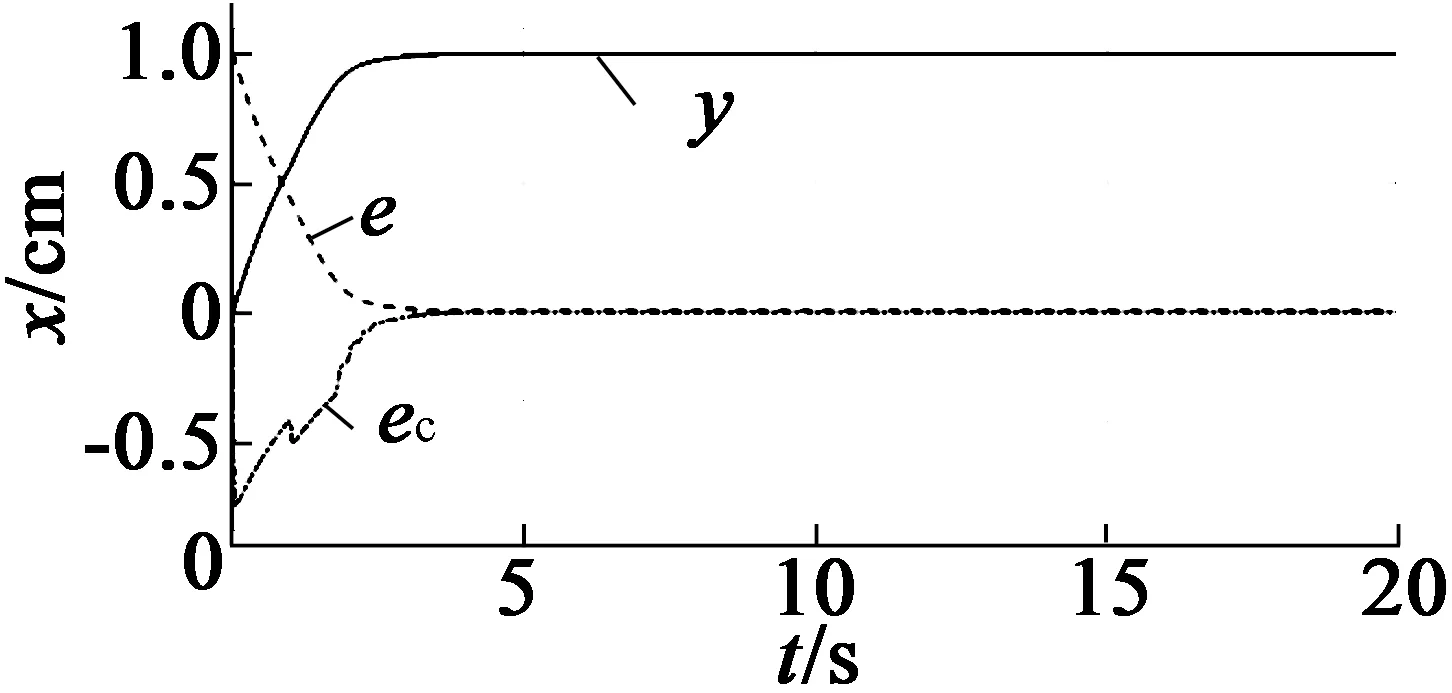
图13 模糊滑模变结构算法仿真曲线

系统运行第5 s时加入扰动，得到模糊滑模变结构扰动响应曲线,如图14所示。由图14曲线可知，当存在脉冲干扰时，系统有超调现象，超调量为7.2%，表明系统抗干扰性能优越，且无抖振现象。

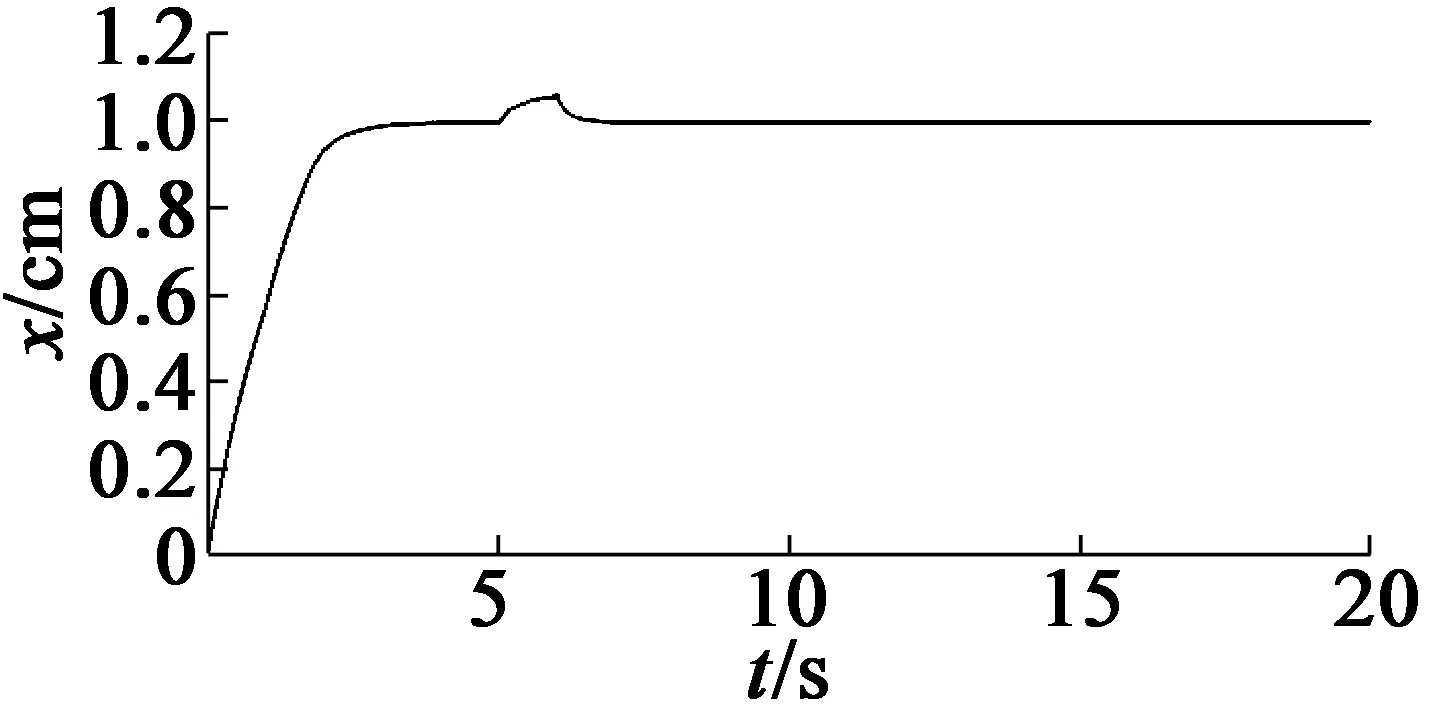
图14 模糊滑模变扰动响应曲线

3.4 原理样机结果

本文利用STM32F407、QT0707力矩电机、PSD传感器，搭建激光雷达扫描振镜硬件原理样机测试平台，如图15所示。采用模糊滑模变结构控制算法得到的PSD数据曲线如图16所示。

在实际系统中要求扫描振镜扫描频率50 Hz，扫描时间为16 ms，复位时间为4 ms。在实际测试中，扫描时间16.1 ms，复位时间3.9 ms，基本达到了期望性能。

图15 扫描振镜原理样机

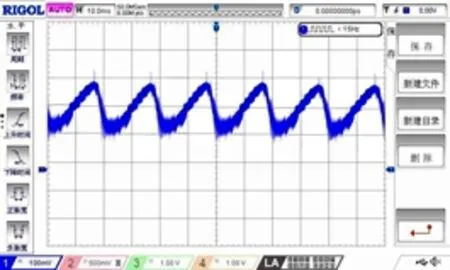
图16 PSD信号波形

分析图16可知，由于实验条件限制，PSD传感器会受到激光光斑大小以及实验室灯光影响，导致正程仍存在一定的抖振现象，反程存在一定超调。

4 结 语

本文建立了激光雷达扫描振镜数学模型，基于PSD位置环进行了模糊PID算法、滑模变结构算法研究并进行了对应的仿真实验，根据模糊PID控制、滑模变结构控制的弊端，提出了新的模糊滑模变结构控制算法，并在Simulink中进行了仿真实验。仿真结果表明，针对激光雷达中扫描振镜控制系统，传统PID可以实现对其控制，但传统PID抗干扰能力不足，无法满足扫描振镜精确控制的需求。模糊PID相比于传统PID算法，抗干扰性能提高，拥有良好的动态控制特性。滑模变结构控制算法在抗干扰性能方面相比于传统PID和模糊PID算法，有较大提升，但固有高频抖振现象限制了其在扫描振镜中的应用。为了解决滑模变结构控制算法这一缺陷，提出了模糊滑模变结构控制算法，将模糊规则融合到滑模变结构控制中，既保留了良好的抗干扰性能，又消除了抖振现象，适合应用于扫描振镜控制。原理样机实验结果与期望结果相符。