双面线性永磁结构的涡流制动性能研究

姜启帆，李玉龙

(西北工业大学，西安 710072)

0 引 言

摩擦制动，即利用摩擦力进行制动的方法，是最传统也是运用最广泛的制动方式。由于摩擦制动是一种接触式的制动方法，受其原理的限制，在频繁或长时间使用时会使制动器温度大大提高，不仅使摩擦片损耗加剧，使用寿命缩短，而且还有可能导致制动效能衰退或者产生火花，存在安全隐患[1-4]。同时，相关研究表明，列车、地铁等高速度、大质量物体的剧烈摩擦制动会产生大量的有害粉尘污染，会对人体健康造成危害[5]。

由于摩擦制动存在一系列难以克服的问题，因此人们开始逐步探索非摩擦的制动方式，能耗制动正是在此背景下的一大尝试。能耗制动指的是借助电磁力来进行制动的方法，将物体的动能转化为电能转移或是热能散发，从而实现减速。能耗制动主要有三种形式：电阻制动、再生制动和涡流制动。受制动作用原理的限制，只有涡流制动才能在没有牵引电机的拖车上使用[6]。现在，在一些游乐场设备、轨道交通工具上，逐渐开始使用能耗制动来进行辅助制动，起到了一定的效果。

1906年，吕登贝格在其博士论文中提出了涡流效应理论，而涡流制动正是在这种理论基础上产生的[7]。涡流制动中，永磁涡流制动是使用永磁体来产生磁场的制动方法，其结构简单，维修方便，不需要通电，因此不会受到线路断电的影响[8]，由于采用开放式设计，故散热也较好。不过与此同时，永磁涡流制动也存在着制动效率低、可调节性差等缺点，还未得到非常广泛的应用。线性永磁制动结构主要分为单面线性永磁涡流制动和双面线性永磁涡流制动两种[9]，结构图如下图1、图2所示，其中，双面线性制动效率要优于单面线性，应用前景也更好，本文就是对双面线性永磁涡流结构进行讨论。肖尧等人对于此结构进行了一定的理论推导，得出了圆形涡流条件下的制动力-初速度关系[10]。本文在此基础上，进一步推导出更具有普遍意义的椭圆形涡流的理论公式，并结合实验以及有限元仿真来验证研究的准确性。

图1单面线性永磁

涡流制动结构

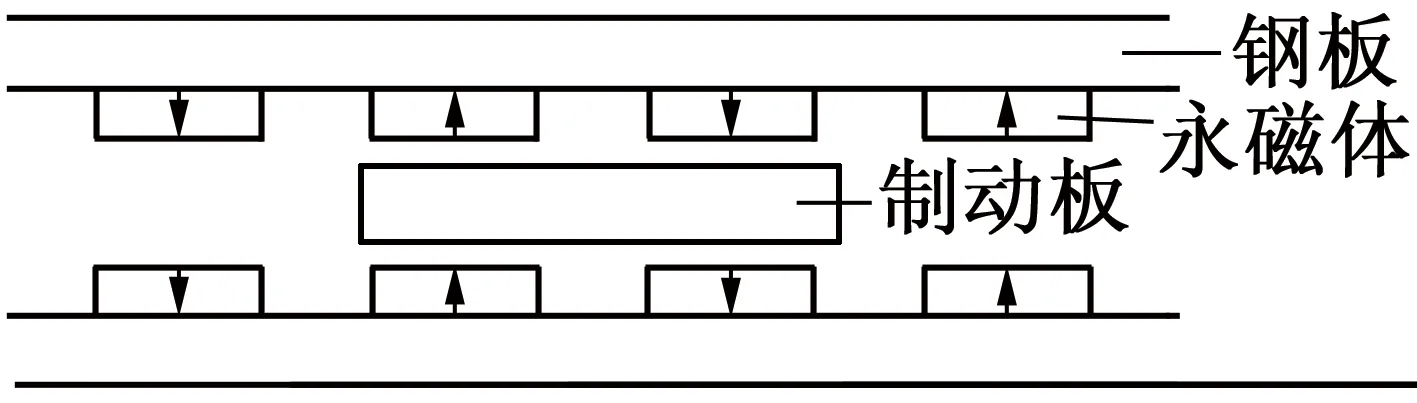
图2 双面线性永磁 涡流制动结构

1 理论推导

双面线性永磁涡流制动结构的初级由钢板和永磁体组成，其N级和S级的排列方式如图2所示。制动板为非导磁的金属板(本文采用铝板)，固定在需要制动的物体上。当制动板在由永磁体产生的磁场中运动时，会切割磁感应线生成涡流，由楞次定律，涡流的磁场与原磁场相反，产生的洛伦兹力与制动板运动方向相反，从而达到减速的目的。从能量的角度来说，就是将制动板的动能通过永磁体与制动板间的电磁作用转化为热能散发[11]。

现对此结构进行理论分析。在此之前，我们要先做几个假设：

1) 忽略整个过程中的温度变化，认为所有部件的电导率、磁导率等参数不变；

2) 认为通过导体板的磁通量以正弦规律变化；

3) 忽略漏磁。

由假设可知，磁通量φ可以表示：

(1)

式中：B为磁感应强度；v为制动板运动速度；b为相邻同性磁极间的距离。

在制动板表面产生的感应电动势E：

(2)

为了能够反映普遍的规律，并简化计算，在本文的推导中，认为永磁体正对制动板的面为长10a、宽6a的矩形，永磁体厚度为2a。于是，在制动过程中，可以认为制动板上产生的涡流形状是长半轴为5a、短半轴为3a的椭圆。将这个椭圆形磁通区域看作由许多长轴∶短轴=5∶3，宽度为Δa、厚度为δ的椭圆环组成，那么椭圆环的电阻ΔR：

(3)

式中：σ为制动板的电导率。

(4)

式中：μ为制动板的磁导率。

于是椭圆形导体环上的功率：

(5)

整个椭圆磁通区域内瞬时功率：

(6)

有效功率：

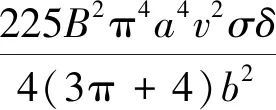
(7)

椭圆导体环上的电流：

(8)

由于电流的正负只代表方向，因此在下面的计算中可以将符号去掉，代表其绝对值。整个椭圆磁通区域内瞬时电流：

(9)

电流有效值：

(10)

接下来对磁路进行分析。由于忽略了漏磁，因此只需要考虑空气、钢板、制动板的磁阻即可。磁路示意图如图3所示。

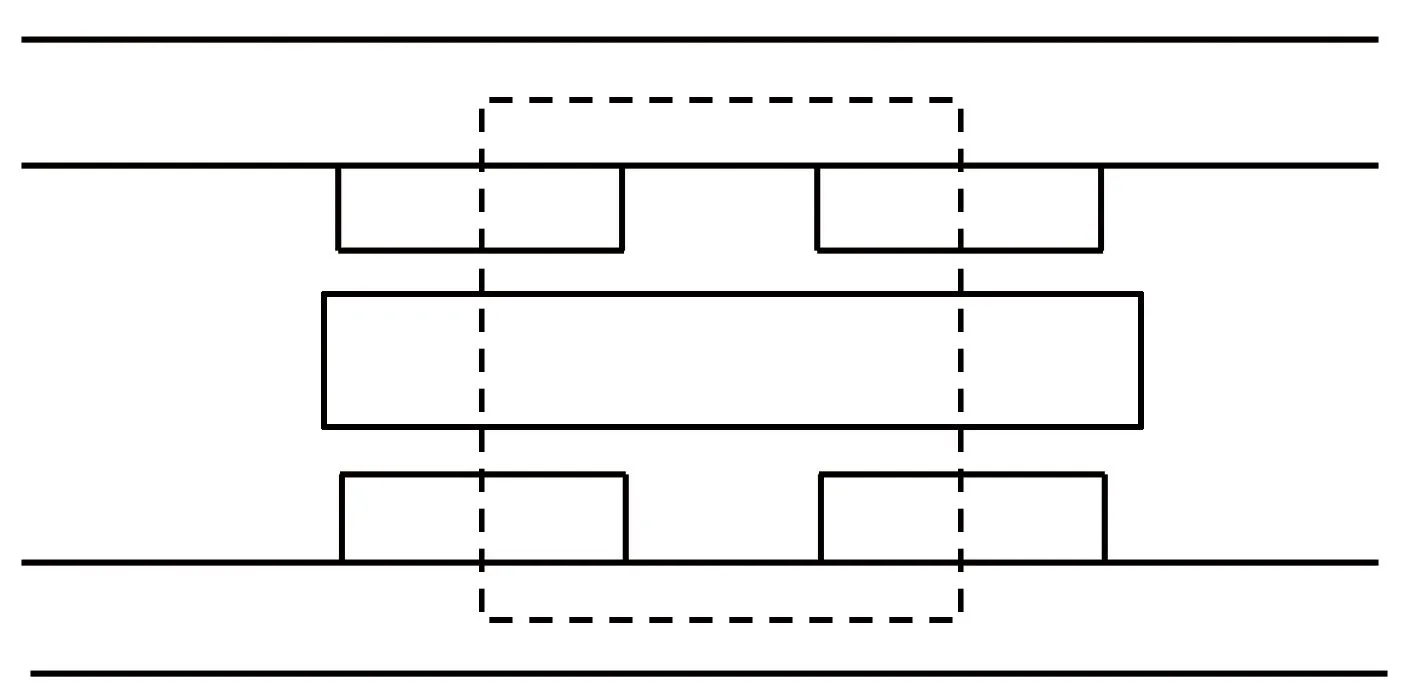
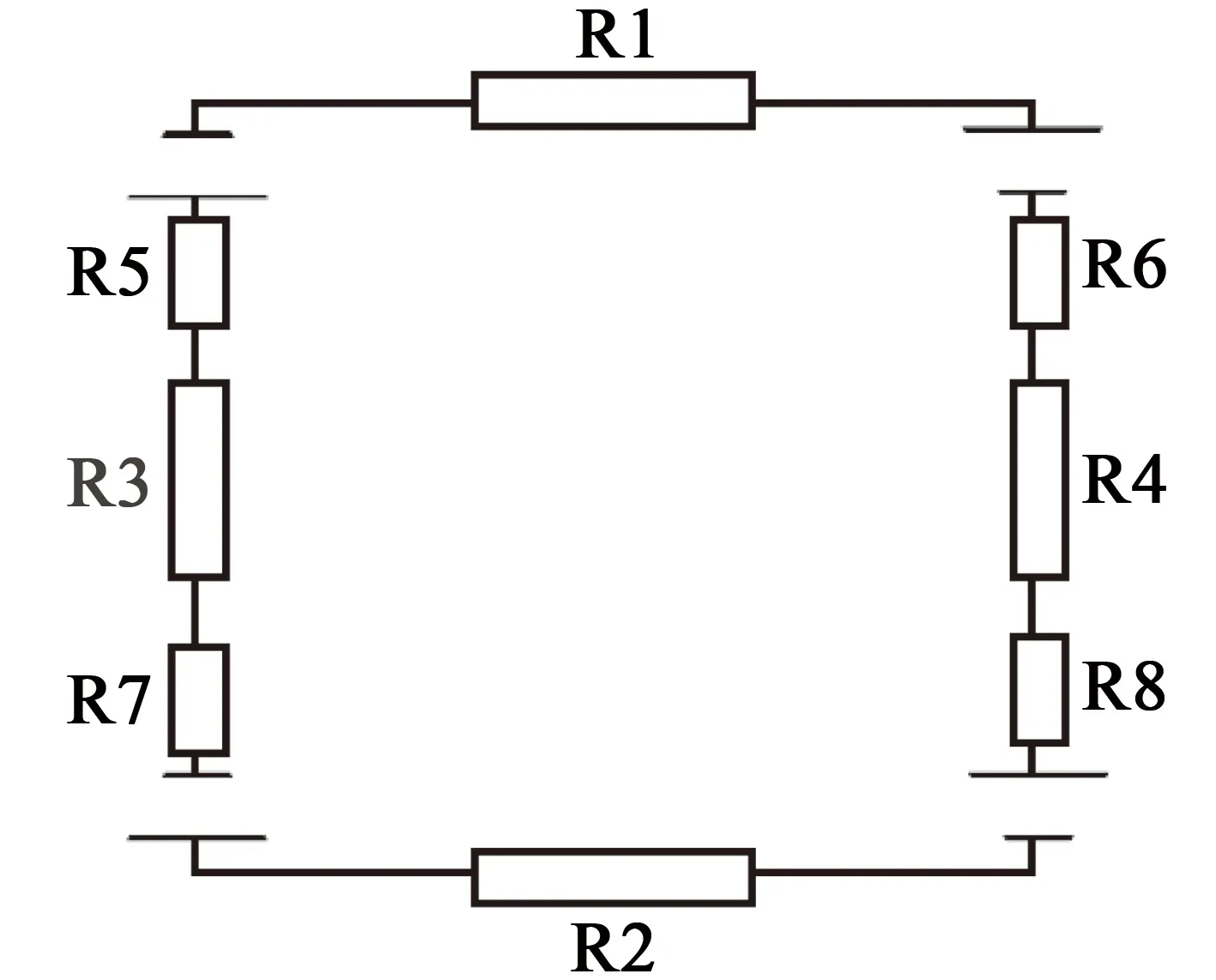
图3 磁路示意图

其中，R1=R2，为钢板中的磁阻；R3=R4，为制动板中的磁阻；R5=R6=R7=R8，为气隙的磁阻。由于磁阻与介质的磁导率成反比，且钢板的磁导率远大于空气和制动板(铝板)，因此可以将钢板的磁阻也忽略。于是磁路总磁阻R：

(11)

式中：g为气隙厚度;h为制动板厚度；S为永磁体正对制动板的面积；μ0为空气磁导率。

磁路的磁动势ξ：

ξ=Hcd-KeIe

(12)

式中：Hc为永磁体矫顽力；d为永磁体厚度；Ke为折算系数。

由环路定理可以得到：

(13)

将式(10)、式(11)代入式(13)，在考虑到对于铝和空气，μ和μ0可以认为相等，于是有：

(14)

制动力F的表达式：

(15)

在获得了制动力-速度关系后，通过牛顿运动定律就可以得到制动过程中的速度-时间关系。

需要注意的是，在这里认为永磁体正对制动板的矩形面的长宽比为5∶3，事实上，对于其他的比例，推导过程类似。

2 实验验证

为验证推导公式的准确性，搭建了小型的双面线性永磁涡流制动装置来进行实验。实验装置的三维模型图及实物图如图4、图5所示。轨道总长为900 mm，由于工艺原因，加工时被分成了450 mm长的两段。因此，为保证轨道的平直性，在两侧及上方用钢制加强块进行了加固。制动块为88 mm×80 mm×14 mm的铝块，上下共加装8个由不导磁的不锈钢轴承制成的轮子。轨道材料为钢，永磁体采用50 mm×30 mm×10 mm的N35钕铁硼磁铁。

图4 实验装置 三维模型图

图5 实验装置实物图 (拆开了一边的轨道)

各参数如表1所示。

制动板采用用强力橡皮筋驱动的圆柱形铝子弹撞击的方法来获得初速度，用V711高速相机记录制动板的整个运动过程，采样频率为4 000 Hz。实验共进行了三组，以下是某组实验的几个特定时刻的照片，如图6所示。对照片进行处理，可以得到在整个过程中制动板的速度-时间曲线，如图7所示。

将三组实验数据进行处理，得到如图8所示的结果。

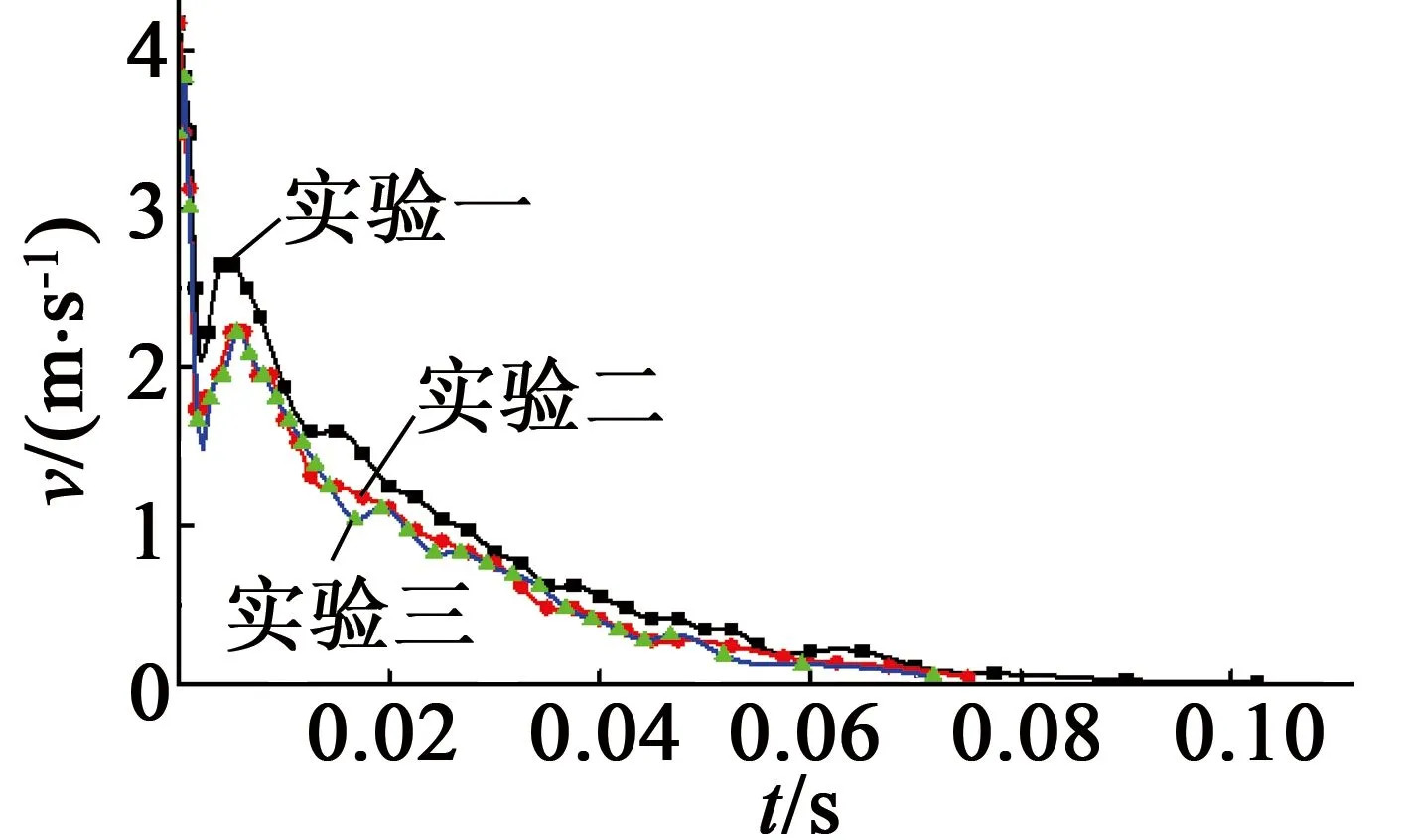
图7 实验所得速度-时间 关系曲线

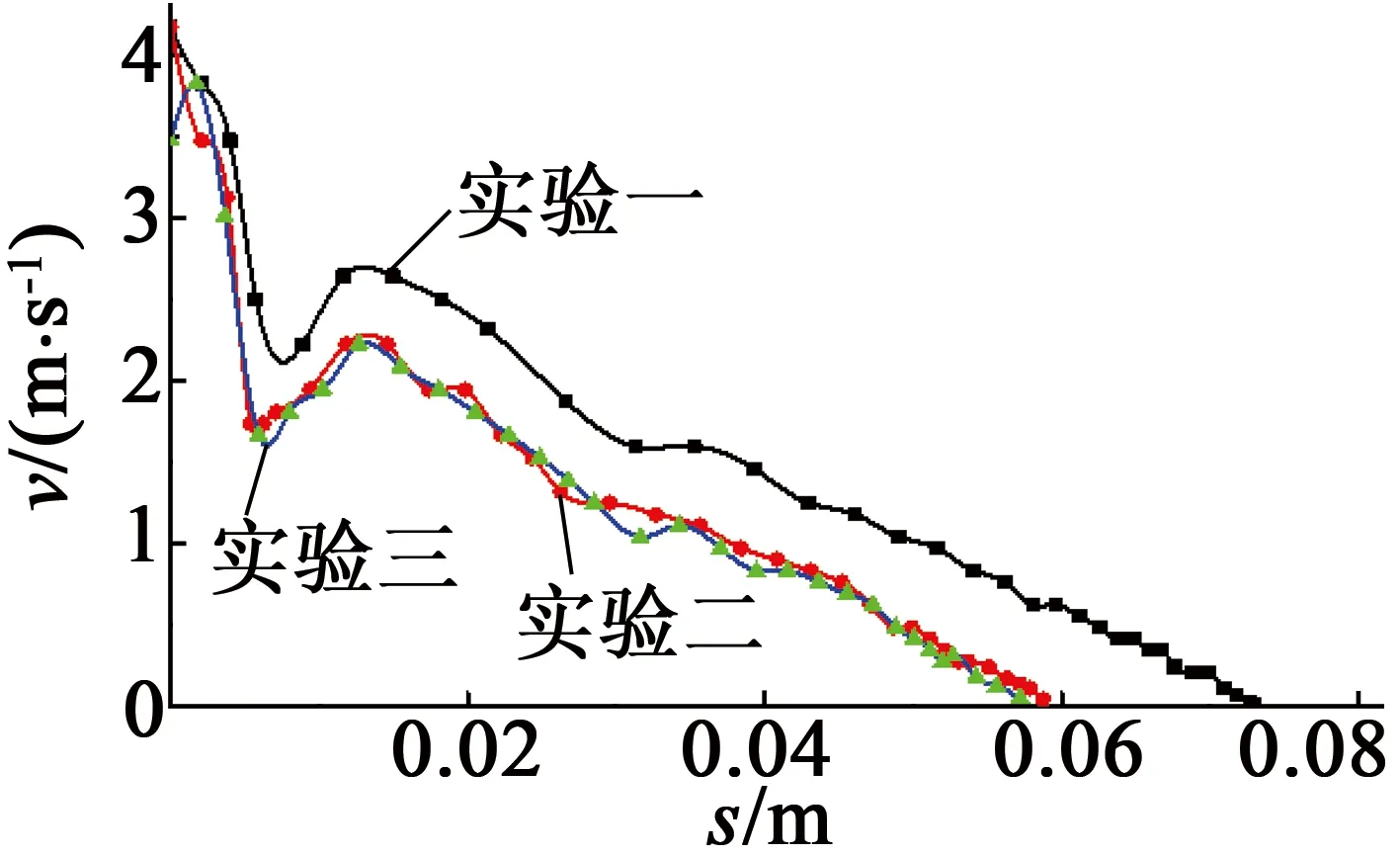
图8 实验所得速度-位移 关系曲线

可以看到，三组实验的重合度较高。另外，可以发现，在实验的初始阶段，与稳定段相比，速度下降较快，且在之后出现了速度增加的现象，这可能是由于子弹撞击点并未完全在制动板的中点，使得制动板的运动不是纯粹的直线运动，而是附加了绕几何中心的转动。在数据处理时，只考虑了水平方向的运动，在尚未稳定的初始阶段会有一定的偏差。通过观察运动过程的照片，也证实了这种猜想。

3 数值仿真

用Ansoft HFSS软件进行数值仿真。Ansoft HFSS是Ansoft公司推出的基于电磁场有限元方法的三维电磁仿真软件，具有高仿真精度和可靠性，快捷的仿真速度，方便易用的操作界面，稳定成熟的自适应网格剖分技术，被广泛应用于航空、航天、电子、通信等领域。建模图如图9所示。

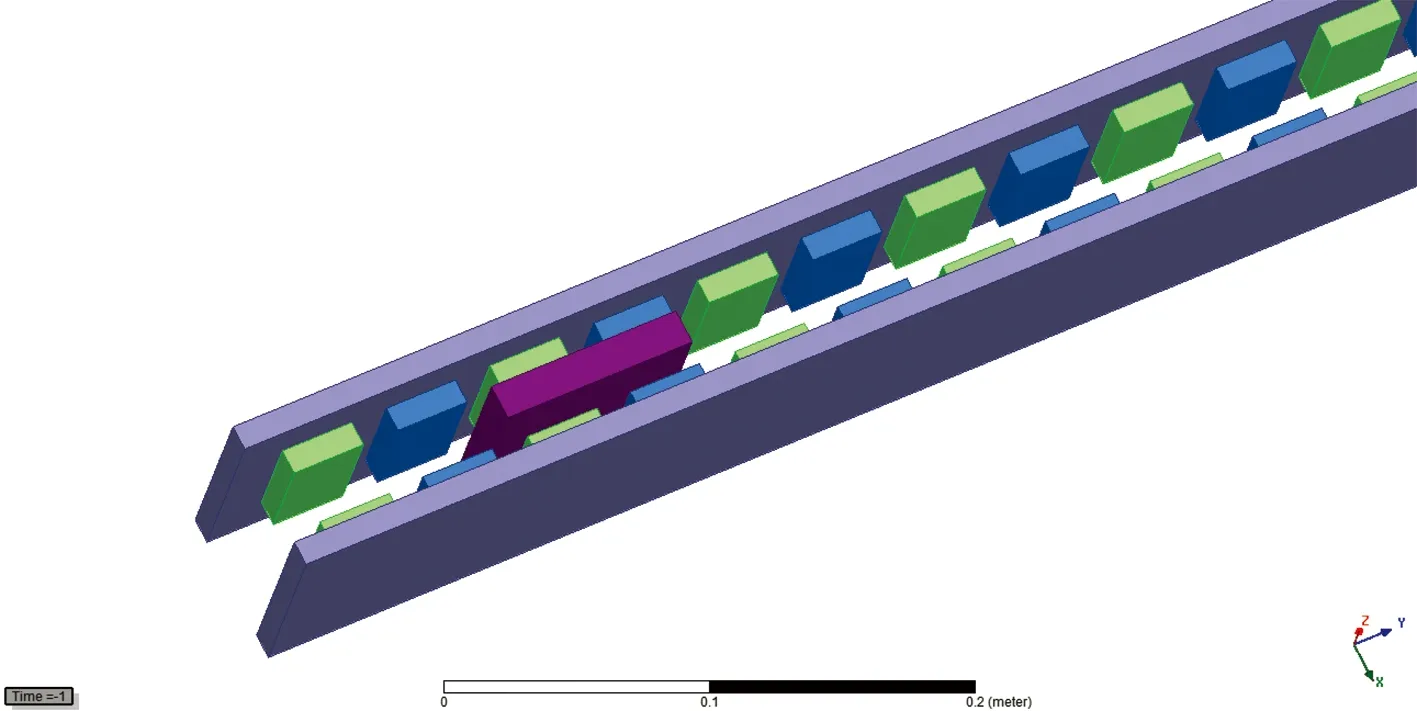
图9 数值仿真

各参数设定和实验中相同，制动板的初速度设定为5 m/s，4.5 m/s，4 m/s,…,0.5 m/s共10组。计算时间为1 ms，步长为0.02 ms。

图10是对于初速度为5 m/s的制动板，在运动1 ms后绘制的制动板内的涡流形态矢量图。可以看出，制动板内的涡流确实是与永磁体正对面几何形态相关的椭圆。

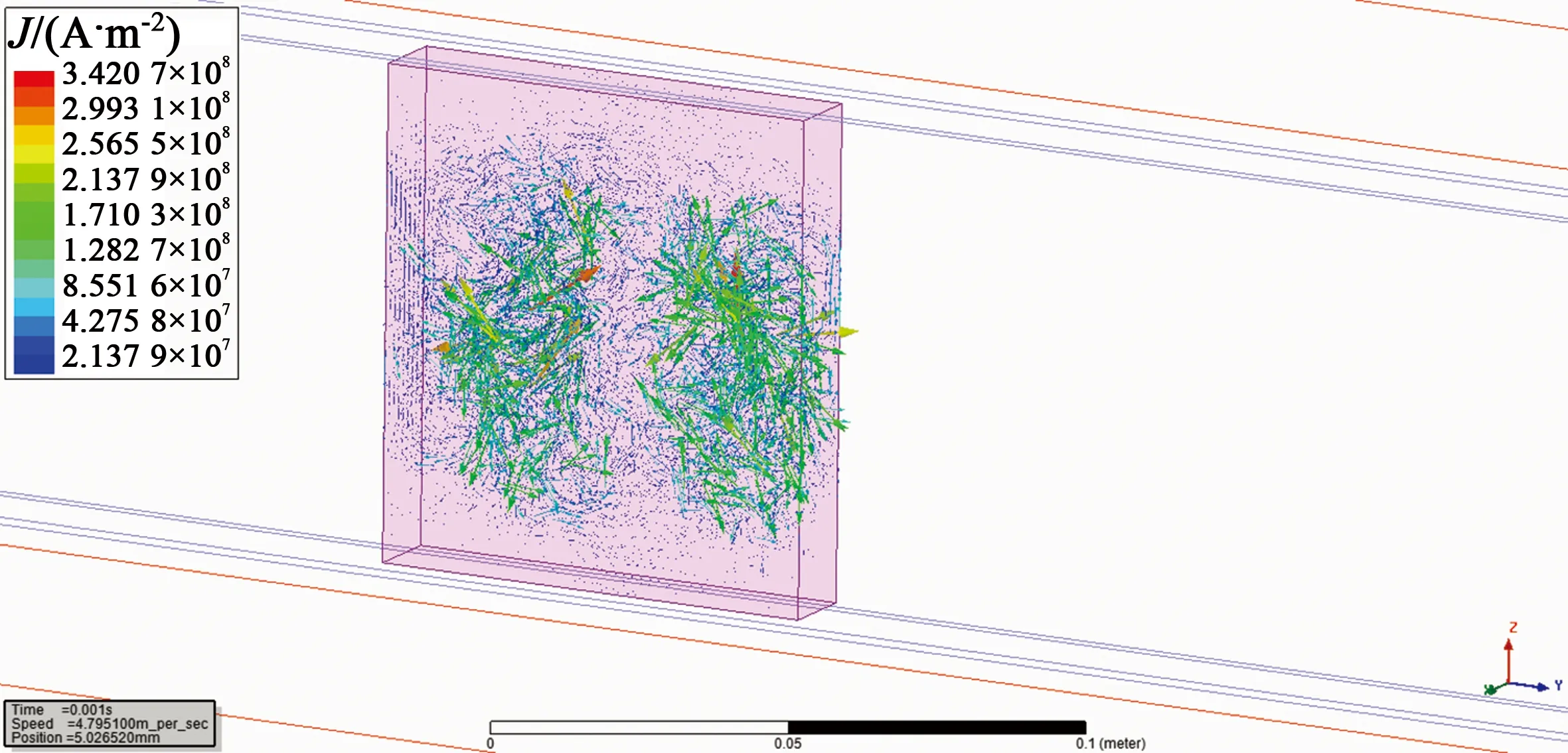
图10 涡流形态矢量图

计算得到一系列数值仿真结果的速度-时间曲线，初速度为5 m/s时的速度-时间曲线如图11所示。对这些曲线进行数据处理，由于计算时间很短(1 ms)，因此可以认为得到的加速度即为瞬时加速度。通过简单的牛顿运动定理，就可以得到整个运动过程的速度-时间关系曲线。

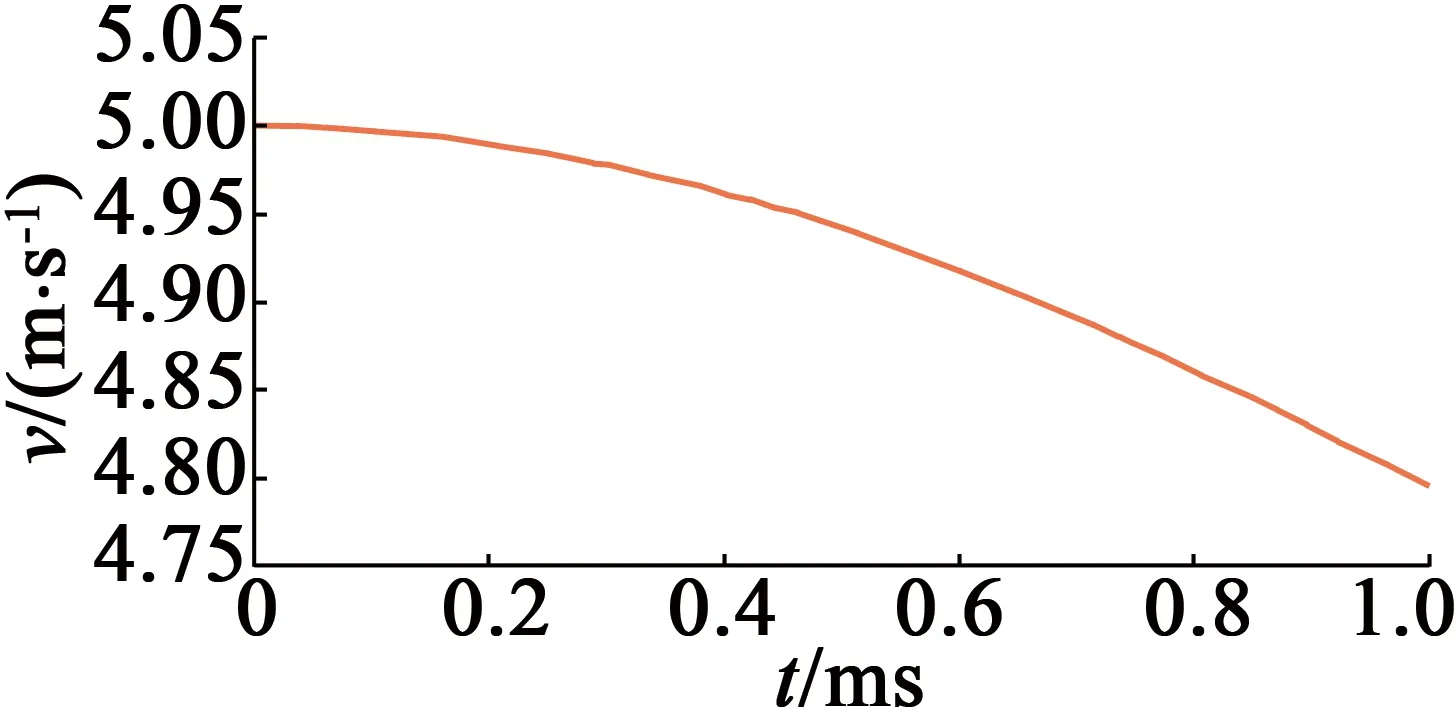
图11 数值仿真中初速度为5 m/s时的速度-时间曲线

4 结 语

将之前得到的理论结果、实验结果以及数值仿真结果汇总到一起，得到如图12所示的结果。

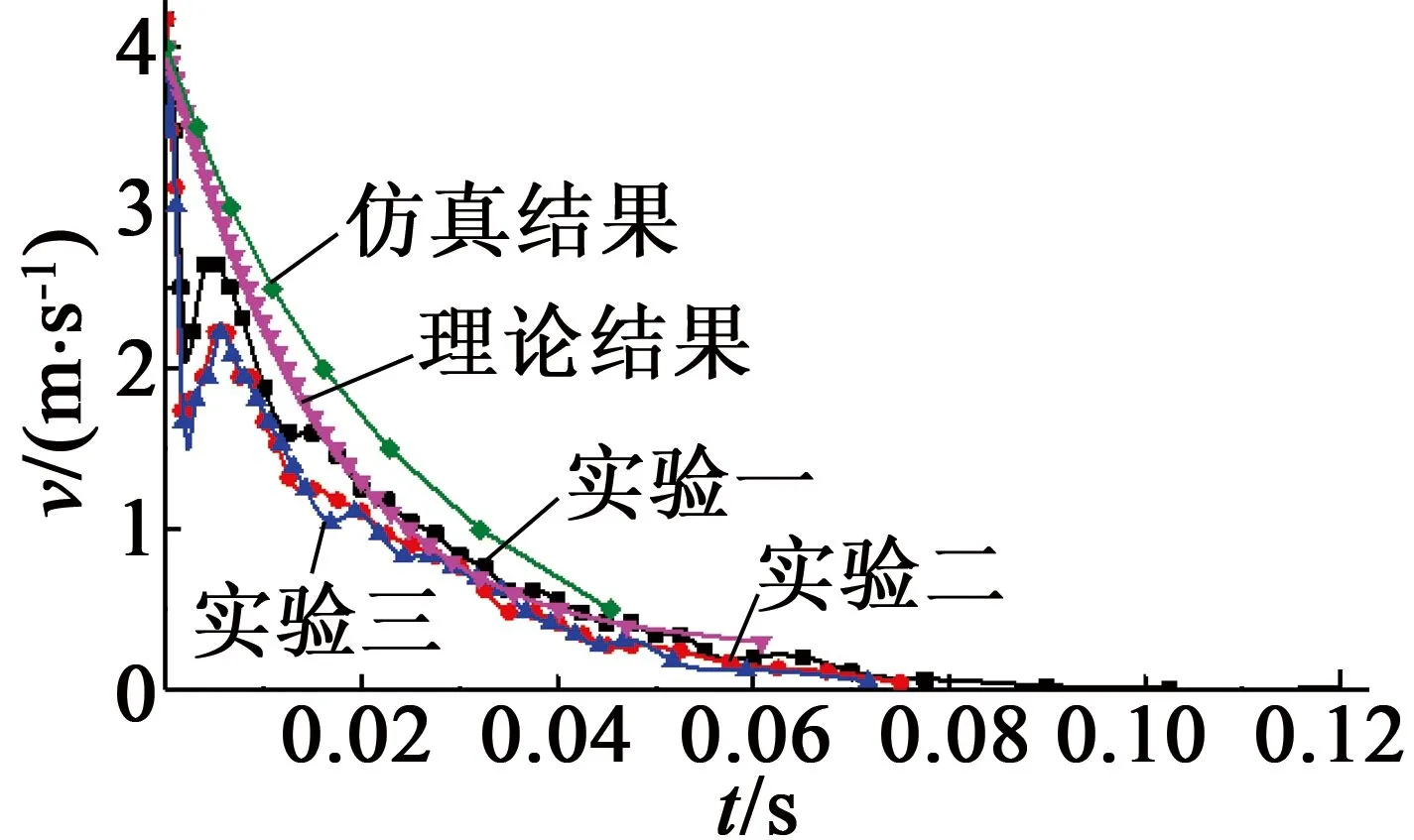
图12 结果汇总

从图12中可见，理论结果、实验结果以及数值仿真结果重合度较高，可以认为之前的推导准确性较高。三者并没有完全重合可能是由以下几方面原因造成的：在理论计算中采用了多个假设，且忽略了漏磁的影响，但在真实情况中并不完全如此；在实验中摩擦力也有一定的制动作用，且为了保证制动块能够流畅滑动，在轨道的设计上留有一定的余量，使得制动块在垂直于导轨方向上的运动并没有被完全约束；在数值仿真中选取的计算点较少，可能会导致精度略低。

通过上述分析，之前得到的理论解与数值仿真的可靠性较高，为之后此结构的进一步研究奠定了基础。