市场偏好、有限套利与特质性波动率溢价之谜

张华平 叶建华

摘 要：实证研究发现，股票特质性波动率在国内外股票市场中存在显著的负向溢价，这被称之为特质性波动率溢价之谜，探究其成因是当前财务学研究的热点之一。本文以中国A股上市公司为样本，采用构建资产组合及回归分析法，发现投资者极端收益率偏好对特质性波动率溢价之谜的解释力较弱，但基于中国A股市场构建的有限套利指标对该资产定价异象存在较强的解释力。本文丰富了特质性波动率负向溢价存在性及成因研究，对于优化中国股票市场规制也具有重要政策启示意义。

关键词：市场偏好;有限套利;资产组合;特质性波动率;溢价之谜

中图分类号：F830.91  文献标识码：A

文章编号：1000-176X（2019）10-0077-09

一、问题的提出

资产价格波动体现了资产的风险，风险如何定价是公司金融学研究中关注的核心问题。根据有效资本市场理论，在充分有效的资本市场中，完全理性的投资者能够以无摩擦、无成本的方式进行交易，并寻求最优风险—收益关系的资产组合。在所有可供选择的资产组合中，涵盖所有资产的市场组合能够分散掉单项资产的异质性风险，而使投资者不用承担异质性风险。鉴于此，所有市场参与者都会理性地选择市场组合，这种最充分的多元化组合能够分散掉所有的异质性风险。

但越来越多的实证研究发现了同经典资产定价模型相违背的现象，也即股票市场中股票的异质性波动率具有显著的资产定价效应。Ang等[1]证明，异质性波动率同随后股票收益率之间存在负相关关系。已实现异质性波动率代表预期异质性波动率的程度决定了该资产定价效应作为一个谜团的程度。这种现象之所以被称之为谜团，在于两个方面的原因：首先，因为经典的资产定价模型假设投资者都能够通过构建最充分的资产组合来分散掉异质性风险，预期异质性波动率同预期报酬率之间不应存在相关关系。其次，放宽完美市场假设时，投资者面临投资摩擦而不能够构建最充分的投资组合，需要承担异质性风险，此时也只能预测二者之间存在正相关关系。基于中国A股市场的样本，杨华蔚和韩立岩[2]也发现较高的异质性波动率股票组合具有较低的预期收益率。针对异质性波动率溢价之谜，国外学者对美国等资本市场进行了诸多研究，并尝试寻求成熟资本市场背景下该资产定价异象的形成机制。但国内学者对中国A股市场异质性波动率溢价之谜的成因探究较少。笔者认为，在中国以中小投资者为主的新兴股票市场存在各种市场摩擦因素，行为因素对异质性波动率溢价效应可能更具有解释力。鉴于此，本文基于有限套利和投资者非理性两大行为金融学视角探究中国A股市场异质性波动率的成因。由于特质性波动率同股票极端收益率密切相关，本文探究了投资者极端高收益率偏好是否能够解释特质性波动率之谜。在套利机制方面，中国A股市场的套利机制受到限制，尤其是对低估值股票的套利机制受限程度更高，也即存在非对称性套利的问题。本文分别从有限套利和非对称性套利视角来探究特质性波动率溢价之谜的成因。

二、文献综述及研究假设

许多研究探究了异质性波动率或风险同预期股票收益率之间的关系。在非完美的股票市场中，投资者难以构建充分多元化的资产组合而分散掉异质性风险，股票异质性波动率与预期收益率之间应该存在正相关关系，许多研究也证明了这种观点。但Ang等[1]发现了相反并令人迷惑的结果，他们的研究表明高异质性波动率资产组合具有异常低的收益率。这种结果通常被认为是“异质性波动率之谜”，因为这种结果表明高异质性波动率需要较低的负向风险溢价。基于中国A股市场背景，国内学者也研究了异质性波动率之谜问题。熊伟等[3]将高、低特质波动率资产组合加权平均收益率之差作为特质风险因素，证明特质风险因子越高，预期股票市场收益率越高。刘维奇等[4]证明特质性之谜存在于中国A股市场，但在控制价格极差、最大日收益率及换手率后，特质性波动率之谜不再存在，说明投资者对特定股票的偏好可能是特质性之谜存在于中国A股市场的原因。熊伟和陈浪南[5]发現，特质性波动率和股票收益率正相关，投资者乐观程度越高、市场流动性越强，高、低特质波动率资产组合收益率的截面差异越大。王春峰等[6]发现，特质性波动率同股票截面收益率间的关系具有分位数依赖性，异质性波动率之谜仅存在于收益率较低的样本股票中，在高收益率股票中，特质波动率与预期股票收益率间存在正相关关系。虞文微等[7]从套利限制视角来解释中国股票市场特质性波动率之谜，发现套利限制程度较高（较低）的样本中，特质性波动率之谜更为（不再）显著。 熊和平等[8]证明中国股票市场中特质风险同预期回报之间存在负相关关系。概括来讲，国内外学者的研究均证明了异质性波动率之谜广泛存在于国外及中国A股市场。

许多文献开始探寻异质性波动率之谜的成因。Fu[9]指出，特质性波动率测量方法是该谜团的成因。Grullon和Zhdanov[10]与Bali等[11]发现，同期的特质波动与股票收益率存在正相关关系，这进一步导致了特质波动率与后期股票收益率存在负相关关系。具体而言，特质性波动率的加大可能会提高公司成长期权的价值，但随着公司对特质性波动率的利用，预期报酬率会降低。Boyer等[12]认为，预期的特质波动率偏差可以解释这种负向关系，而Bali等[11]表明，上月份的最大日收益率可以解释该谜团。Han和Kumar[13]认为，中小投资者的交易可以解释该谜团。Jiang等[14]认为，投资者过度自信以及昂贵的套利成本会导致高特质性波动率股票被高估，并且由于短期卖空限制的存在会加剧价格的偏离度，进而加剧了特质波动率与未来收益率间的负相关关系。Huang等[15]证明，高特质性波动率股票的收益率反转可以解释特质性风险的负向价格效应。学者们虽研究发现中国A股市场存在特质性波动率之谜，但只探究该谜团成因的研究相对较少。杨宏林等[16]研究发现，融资融券交易影响股票特质性波动率，进而可能有助于解释特质性波动率之谜。戴方哲和尹力博[17]发现，证券分析师预测偏差影响特质性波动率，并指出特质性波动率之谜可能与分析师预测偏差有关。概括而言，现有关于特质性波动率之谜的研究关注的焦点在于不同特性波动率股票的特质差异以及市场状况如何影响特质性波动率—期望收益率关系，国内学者有关特质性波动率成因之谜的研究更少。本文则探究不对称性套利、投资者偏好特质对特质性波动率之谜的影响。

三、理论分析与研究假设

经典金融理论难以解释资产定价异象等许多现实资本市场中的现象。行为金融理论放宽了传统金融理论中套利价值有效性和投资者理性两大假设。在此基础上，有限套利和投资者行为假设称为行为金融的两大基石。在资本市场套利机制受限时，非理性投资者的交易导致的错误定价难以被理性投资者的套利行为所消除并会持续存在下去。中国作为最大的新兴股票市场，构成市场投资者主体的中小投资者具有显著的非理性特质，对市场的影响更大。此外，由于中国A股市场存在涨跌停限价制度、有限的融资融券交易制度和非完全的股指期货制度，这些非市场化的制度因素也会在一定程度上限制了套利机制在中国股票市场的有效性。在此背景下，中国股票市场存在许多资产定价异象能够被行为金融理论解释。叶建华[18]证明，中国A股市场中投资者对月度内产生极端高收益率的股票具有热手效应心理，倾向于非理性预期此类股票会继续产生高收益，进而偏好月度内产生极端高收益率的股票，也即存在极端高收益率偏好，致使此类股票被高估。投资者偏好极端高收益率股票的心理可解释中国A股市场中的极大日收益率效应。此外，由于股票特质性波动率同股票的极端波动率密切正相关，或者说特质性波动率高的股票更可能产生极端高收益率。因此，本文可以合理推断，投资者对极端高收益率的偏好理性能够解释中国A股市场的特质性波动率溢价之谜。鉴于此，笔者提出假设1：

假设1：在中国A股市场存在特质性波动率之谜，投资者极端高收益率偏好对特质性波动率之谜有一定解释力。

在非理性投资者因偏好极端高收益率而高估特质性波动率较高的股票時，套利限制可能妨碍股价迅速回归至其基本价值。Delong等[19]指出，噪音交易者可以在更长时期内推动价格显著偏离内在价值而给套利者带来套利风险。Shleifer和Vishny[20]表明，套利活动需要成本，并且当市场价格严重偏离基本价值时，套利活动会无效果。近期实证文献检验了有限套利对多种市场异象的影响，包括账面市值比效应、动量效应、应计异象以及资产增长异象。在资产发生错误定价时，套利机会吸引理性套利者实施套利活动，股价随后恢复至其基本价值时给套利者带来套利收益。套利成本、套利风险、交易限制以及信息不确定性等因素会限制套利活动。在中国特殊的制度背景下，套利风险包括非理性投资者的交易继续驱动价格偏离基本价值的风险，套利限制主要是非市场化的制度因素。中国A股市场的涨跌停制度、局部融资融券交易制度和有限的估值期货制度等因素都是套利限制因素。此外，根据Stambaugh等[21]的观点，特质性波动率的负向收益率溢价产生的原因可能是套利的非对称性。具体而言，投资者更容易购买被低估的股票而较难短期做空被高估的股票。因此，错误定价在高估的资产中更严重。据此，可以合理推断，由于投资者偏好极端高收益的股票而高估这些股票时，套利限制可能会妨碍此类被高估的股票迅速回归至其基本价值，有限套利对特质性波动率负向溢价之谜应该具有一定解释力。据此，笔者提出假设2：

假设2：在套利受限程度较高的股票中，特质性波动率负向溢价之谜更显著。

四、研究设计

（一）样本及数据来源

本文以2002—2017年中国A股上市公司为样本，剔除了ST、*ST公司，剔除了金融类公司及数据不完全的公司，并对关键变量进行了缩尾处理。股票交易数据来源于CSMAR数据库，Fama和French[22]中的三因子数据来源于RESSET金融研究数据库。

（二）变量设计

1.预期特质风险的估计

现有文献主要采用两种方法估计预期特质风险，包括：直接利用滞后1期已实现特质波动率作为预期特质波动率的替代变量;利用时间序列模型估计预期特质波动率。第一种方法隐含的假设是特质波动率服从随机分布。本文借鉴左浩苗等[23]的方法估计特质波动率。

首先，用每只股票每月交易率数据分别估计Fama和French[22]三因子模型，也即用月内个股超额收益率对市场因子（MKTt）、规模因子（SMBt）和价值因子（HMLt）进行回归，回归模型如下：

Rit-rf=αit+βiMKTt+SiSMBt+hiHMLt+εit（1）

其中，MKTt，SMBt，HMLt分别表示t月份的市值因子、规模因子和账面市值比因子，Rit，rf分别表示i股票在t期的毛收益率和无风险收益率。

其次，用估计的三因子模型预测个股的期望收益及残差。按照Ang等[1]的做法，用第i只股票第t个月实现的月度特质波动率定义为模型（1）残差的标准差，表示为IVOLi，t。

2.异常收益率

本文首先根据月度数据估计每只股票月度超额收益率预测模型（1），然后根据模型（1）的估计结果计算的每只股票月度收益率的预测值同实际值的差额作为异常收益率的代理变量，表示为ARit。

3.有限套利的衡量

现有研究表明，在中国A股特殊制度背景下，股票流动性[24]、月度股价涨跌停次数[25]、卖空交易活跃程度[26]以及是否纳入CIS300股指期货指数等四个关键因素是影响A股市场套利受限的重要因素。通常流动性越弱、涨跌停次数越多、融资融券活跃度越低或没有纳入CIS300估值期货指数，则意味着该股票的套利受限程度越高。鉴于此，本文在每月份根据上述单项指标，按流动性从弱到强的次序分别把样本等分为3组，各组用0，1，2表示，计算各样本在本月的各组别之和以此作为衡量本期股票的套利受限程度，该综合指标越大，意味着套利受限程度越高。

4.月度极端收益率

同Bali等[11]的研究不同，本文基于中国A股市场涨跌停限制制度的背景下，首先计算每月内5日移动平均收益（MAXit），以5日移动平均收益率最大值衡量极端日收益率，然后从如下几个视角讨论彩票类股票偏好对异质性波动率定价的影响。

5.公司估值水平的衡量

本文借鉴Stambaugh 等[21]的方法，利用资产定价异象变量构建低估或高估程度的指标。本文基于中国A股市场资产定价异象的状况，并考虑数据可获得性，采用5个单项资产定价异象指标来构建综合指标测量股票被高估或低估的程度，包括总应计利润、净经营资产、盈利能力、惯性指标和股权净筹资额。

本文按照如下步骤来构建股票估值水平的综合衡量指标。首先，计算出每个异象指标。其次，每月分别根据各单项指标把所有样本等分为10组，确定每个样本的10分位值，具有最高预期收益率的观测值的10分位值为10，具有最低预期收益率的观测值的10分位值为1。最后，每月份计算5个10分位数的算术平均值作为综合指标来衡量股票的股指水平。

五、实证结果及分析

（一）特质性波动率负向溢价效应存在性检验

1.根据特质性波动率构建资产组合检验

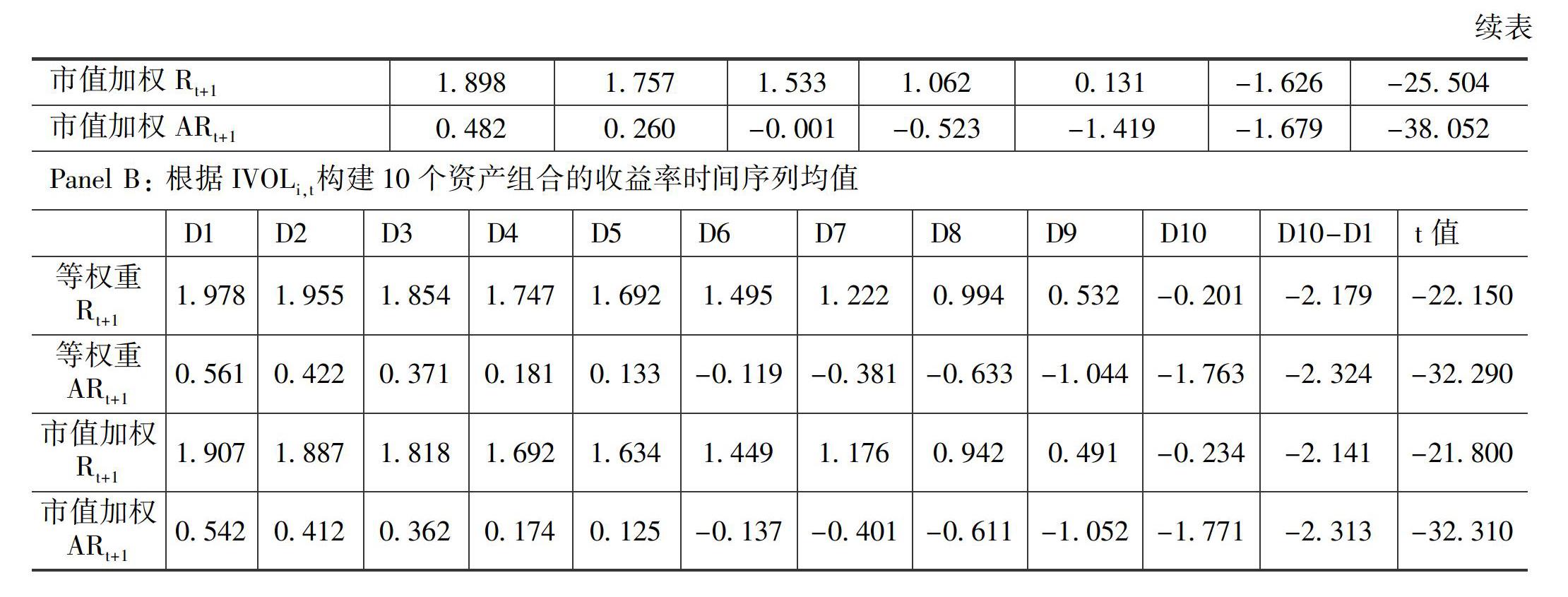
借鉴资产定价异象研究的常规做法，本文通过构建套利资产组合的方法来验证特质性波动率是否存在于中国A股市场。在t月份，根据个股特质性波动率水平，分别构建5、10个资产组合，并进一步计算各资产组合在t+1月份的毛收益率和异常收益率的截面均值，然后计算各资产组合截面均值的时间序列均值。

表1显示了根据t月份个股特质波动率指标构建的各资产组合对应的t+1月份的毛收益率和异常收益率。由表1可知，不论是构建5分位还是10分位资产组合，组合毛收益率及异常收益率均随着特质性波动率的增大而降低。譬如，在构建5分位资产组合时，从极低到极高特質性波动率资产组合的等权重毛收益率（异常收益率）分别为1.961（0.501），1.805（0.271），1.592（0.011），1.112（-0.501）和0.162（-1.402），极端组间差异为-1.643和-1.673且均显著，这初步说明特质性波动率显著地存在于中国A股市场。

2.回归分析检验

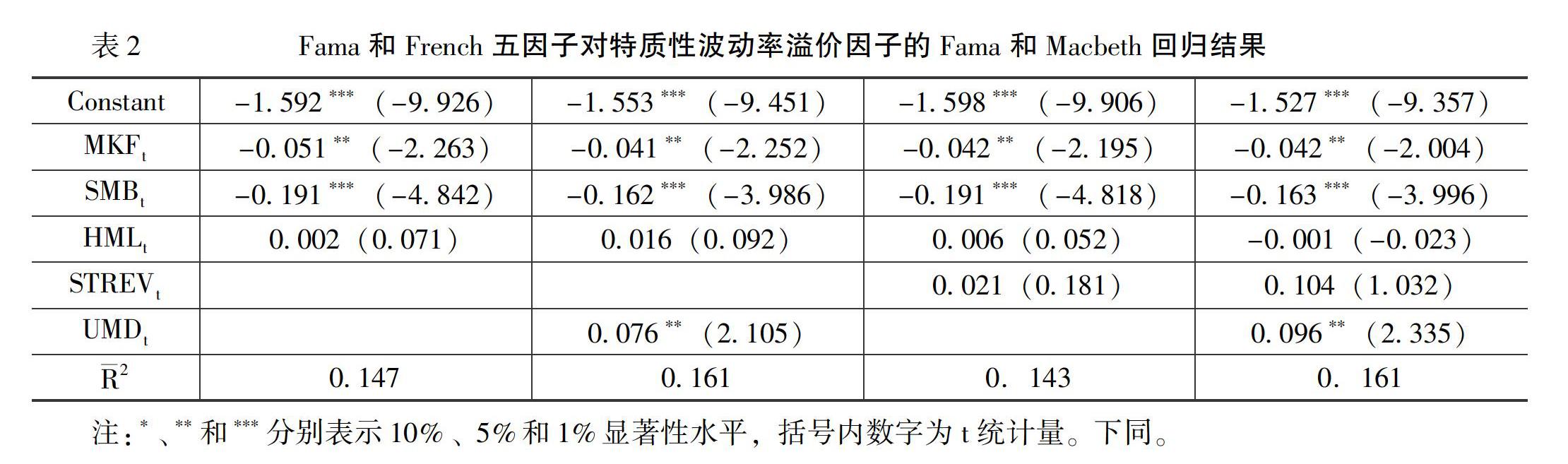
特质性波动率负向溢价可能被已知的风险因子解释。Huang等[15]认为月度股票收益率反转现象可解释Ang等[1]发现的异质性波动率溢价。为排除这种可能性，本文验证Fama和French[27]的五因子能够解释特质性波动率负向溢价，获取特质性波动率负向溢价能否被已知风险因子所解释及是否稳健存在的证据。首先，根据特质性波动率构建5分位资产组合，并计算极端组合毛收益率截面收益率差异，称之为特质性波动率溢价因子。其次用Fama和French[27]五因子对特质性波动率溢价因子回归，Fama和Macbeth[28]的回归结果如表2所示。

表2显示了用Fama和French[27]五因子对特质性波动率溢价因子的Fama和Macbeth[28]回归的结果。可以看出，引入传统的三因子后，常数项仍显著为负值，并且在控制短期反转因子及动量因子后，常数项仍显著为负值（-1.592在1%的水平上显著）。这说明在中国A股市场，已知的三因子和五因子均不能对特质性波动率溢价做出有效的解释，特质性波动率溢价稳定存在于中国A股市场。

概括来讲，分组检验及Fama和Macbeth[28]回归结果提供的证据表明，特质性波动率溢价稳定地存在于中国A股市场，并且已知的风险定价因子对特质性波动率负向溢价并不具有替代解释力。

（二）投资者极端高收益偏好与异质性波动率溢价

本部分检验异质性波动溢价源于投资者偏好彩票类股票的解释。首先，本文基于上月份的MAX5i，t把股票分为10组。其次，把每个MAX5i，t组合再根据IVOLi，t等分为10组。最后，把每个MAX5i，t组合中，最高IVOLi，t组合同最低IVOLi，t组合收益率差额作为该MAX5i，t组合中的IVOL溢价率。

资产组合收益率报告在表3中。IVOLi，t溢价率等于最高（D10）和最低（D1）异质性波动率资产组合的平均收益率差额。表3表明，不管是一维还是二维分组，D10和D1的差额均显著为负值。在一维分组时，最高异质性波动率组（D10）同最低异质性波动率组（D1）等权重Ri，t+1，ARi，t+1，AR5i，t+1收益率均值差异分别为-2.172，-2.328和-2.236，市值加权重Ri，t+1，ARi，t+1，AR5i，t+1收益率均值差异分别为-2.137，-2.319和-2.217。在二维分组时，最高异质性波动率组（D10）同最低异质性波动率组（D1）等权重Ri，t+1，ARi，t+1，AR5i，t+1收益率均值差异分别为-1.499，-1.070和-1.294，市值加权重Ri，t+1，ARi，t+1和AR5i，t+1收益率均值差异分别为-1.495，-1.078和-1.275。上述资产组合收益率差异均在1%水平上显著。说明中国A股市场IVOLi，t溢价稳定存在，在控制MAX5i，t后，IVOLi，t溢价水平虽有所下降但仍旧显著。

整体而言，表3表明，在中国A股市场，异质性波动率的资产定价效应主导了彩票类支付特征（例如MAX5i，t）的定价效应。在控制MAX5i，t后，IVOLi，t溢价仍旧显著而稳定存在。这说明，投资者对彩票类支付特征股票的偏好并不能很好地解释中国A股市场当中的异质性波动的负向溢价效应。

（三）套利受限与异质性波动率负向溢价

本部分将研究有限套利对异质性波动率溢价的解释力。Stambaugh等[21]认为，IVOL同随后收益率之间的负相关关系可以由卖空限制导致的不对称性套利解释。该研究发现，在低估的股票中，存在较弱的正向IVOL溢价，但在被高估的股票中，存在较强的负向IVOL溢价。因此，二者综合起来后，条件IVOL溢价为负值。本部分检验IVOL溢价同股价高估或低估的关系状态是否在中国股票市场也成立，尤其是在套利水平不同的股票中是否成立。

1.基于3个变量构建套利资产组合

本文构建了三维的资产组合。首先，根据综合有限套利指标把各月份样本等分为低、中、高三类有限套利组;其次，在各有限套利组内，根据综合估值水平指标把各类样本再等分为3组;最后，根据异质性波动率把根据有限套利程度、估值水平确定的各资产组合，等分为5组。在控制有限套利程度及估值水平后，计算出由异质性波动率确定的5个独立资产组合。本文计算了各三维度资产组合在t+1月份价值加权毛收益率均值以及Fama和French[22]三因子风险调整收益率均值，结果如表4。

在表4中，报告了每个有限套利及估值水平决定的资产组合内部，高异质性波动率资产组合、低异质性波动率资产组合的收益率差异。在比较不同估值水平资产组合中异质性波动率溢价水平差异时，本文发现Stambaugh等[21]提出的不对称性套利理论对低有限套利组中IVOL溢价的解释力最强，在低、中有限套利组中也具有一定的解释力。对比Panel A和Panel B可以发现，在高有限套利组合内，根据毛收益率（三因子模型风险调整收益率）计算的低、中、高估值水平资产组合中IVOL溢价率水平分别为-2.427（-2.332），-2.722（-2.655）和-2.961（-2.934），且均在1%的水平上显著。低、中有限套利资产组合内，根据毛收益率和三因子模型风险调整收益率计算的高、中、低估值水平资产组合的IVOL溢价率水平虽有所增加，但增幅相对较小。此外，在高有限套利样本内部，按照毛收益率和三因子风险调整收益率计算的最高估值组、最低估值组IVOL溢价率差额分别为-0.534和-0.612，显著性水平均为5%，而在低、中有限套利组中，高、低估值组的IVOL溢价率差额并不显著。这也再次证明，在高有限套利组中，非对称性套利对IVOL的解释力成立，但在低、中有限套利样本中，非对称性套利对IVOL也具有一定的解释力。

2.回归分析检验

概括来讲，分组检验结果表明，在低、中、高有限套利程度样本中，高估值公司产生了更大幅度的负向异质性波动率溢价。为进一步证实非对称性套利对IVOL溢价的影响，解释异质性波动对超额收益率的影响程度，本文采用Fama和Macbeth[28]的方法计算的定价因子对超额收益率分步回归结果，以此验证有限套利、估值水平及股票异质性波动率对超额收益率的影响，结果如表5所示。

第1步回归结果表明，Overpi，t×IVOLi，t和Undpi，t×IVOLi，t的斜率系数分别为-0.490和-0.457，且均在1%的水平上显著，这说明在高估值公司中，IVOL溢價率更明显，这同分组检验获取的证据一致。

第2步回归结果表明，Overpi，t×IVOLi，t，L_limi，t×Overpi，t×IVOLi，t和H_limi，t×Overpi，t×IVOLi，t的斜率系数分别为-0.520，-0.216和0.074，且均在1%的水平上显著，这说明在低（高）有限套利样本中，高估值公司IVOLi，t的斜率系数为-0.736（-0.446）。

第3步回归结果表明，Undpi，t×IVOLi，t，L_limi，t×Undpi，t×IVOLi，t和H_limi，t×Undpi，t×IVOLi，t的斜率系数分别为-0.510，-0.147和0.186，且均在1%的水平上显著，这说明在低（高）有限套利样本中，低估值公司IVOLi，t的斜率系数为-0.657（-0.324）。

第4步回归结果表明，Overpi，t×IVOLi，t，L_limi，t×Overpi，t×IVOLi，t和H_limi，t×Overpi，t×IVOLi，t的斜率系数分别为-0.501，-0.215和0.088，且均在1%的水平上显著，此时在低（高）有限套利样本中，高估值公司IVOLi，t的斜率系数为-0.716（-0.413）。Undpi，t×IVOLi，t，L_limi，t×Undpi，t×IVOLi，t和H_limi，t×Undpi，t×IVOLi，t的斜率系数分别为-0.508，-0.151和0.191，且均在1%的水平上显著，此时在低（高）有限套利样本中，低估值公司IVOLi，t的斜率系数为-0.659（-0.317）。

上述证据说明，不论是低、高有限套利样本，高估值公司的异质性波动率对超额收益率均产生了更大幅度的负向影响。

整体而言，本文实证检验结果表明，特质性波动率溢价稳定地存在于中国股票市场;投资者对极端高收益率股票的偏好并不能解释特质性波动率负向溢价之谜;有限套利对异质性波动负向溢价率的解释能力不仅在美国等发达市场成立，在中国这一发展中股票市场同样具有解释力。

六、结论与启示

本文基于中国A股市场背景特征，构建了由4项单独指标组成的综合指标来衡量中国A股市场股票的有限套利程度，主要采用构建套利资产组合检验及Fama和Macbeth[28]回归分析方法，检验了中国A股市场异质性波动率的定价效应及有投资者极端高收益率偏好、有限套利对该定价效应的解释力。研究发现，中国A股市场存在显著的异质性波动率负向溢价效应，并且该负向溢价程度在有限套利程度较高的样本中更明显，投资者对极端高收益率股票的偏好并不能有效解释特质性波动率负向溢价之谜。

本文证明丰富了有关特质性波动率溢价之谜的研究，并从行为金融视角探究了特质性波动率溢价之谜的成因，拓展了有关特质性波动率负向溢价之谜成因的研究，也具有一定的政策启示意义。在发展中股票市场，为保护投资者利益，实施了多种有特色的市场规制。譬如，中国A股市场中的涨跌停制度、部分股票融资融券交易制度、股指期货制度等，这些制度实际上限制了市场机制的发挥，增加了套利难度。投资者更可能持有异质性波动率较高的股票，致使此类股票被高估并产生较低的随后收益率，放松市场管制有助于降低类似错误定价的程度。

参考文献：

[1] Ang，A.， Hodrick， R.， Xing， Y.， et al.The Cross-Section of Volatility and Expected Returns[J].The Journal of Finance， 2006， 61（1）：259-299.

[2] 杨华蔚，韩立岩.外部风险、异质信念与特质波动率风险溢價[J].管理科学学报，2011，（11）：71-80.

[3] 熊伟，陈浪南，柯忠义.股市特质风险与股票收益率相关关系的实证研究[J].管理工程学报， 2017，（2）： 170-176.

[4] 刘维奇， 邢红卫， 张信东.投资偏好与“特质波动率之谜”——以中国股票市场A股为研究对象[J].中国管理科学， 2014，（8）： 10-20.

[5] 熊伟， 陈浪南.股票特质波动率、股票收益与投资者情绪[J].管理科学， 2015，（5）： 106-115.

[6] 王春峰， 姚守宇，房振明.收益率厚尾分布、特质性波动与股票价格行为[J].系统工程， 2017，（12）： 1-14.

[7] 虞文微， 张兵，于琴.套利限制与中国股票市场“特质波动率之谜”[J].北京工商大学学报（社会科学版）， 2017，（6）： 93-103.

[8] 熊和平，刘京军，杨伊君，周靖明.中国股票市场存在特质波动率之谜吗？——基于分位数回归模型的实证分析[J].管理科学学报， 2018，（12）： 37-53.

[9] Fu， F.Idiosyncratic Risk and the Cross-Section of Expected Stock Returns[J].Journal of Financial Economics， 2005， 91（1）：24-37.

[10] Grullon， G.， Zhdanov， E.L.Real Options， Volatility， and Stock Returns[J].The Journal of Finance， 2012， 67（4）：1499-1537.

[11] Bali， T.G.， Cakici， N.， Whitelaw， R.F.Maxing out： Stocks as Lotteries and the Cross-Section of Expected Returns[J].SSRN Electronic Journal， 2009， 99（2）：427-446.

[12] Boyer， B.， Mitton， T.， Vorkink， K.Expected Idiosyncratic Skewness[J].Review of Financial Studies， 2010， 23（1）：169-202.

[13] Han，B.， Kumar，A.Speculative Retail Trading and Asset Prices[J].Social Science Electronic Publishing， 2013， 48（2）：377-404.

[14] Jiang， D.， Peterson， D.R.， Doran， J.S.Short-Sale Constraints and the Idiosyncratic Volatility Puzzle： An Event Study Approach[J].Journal of Empirical Finance， 2014， 28（9）：36-59.

[15] Huang， W.， Liu， Q.， Rhee， S.G.， et al.Return Reversals， Idiosyncratic Risk， and Expected Returns[J].Review of Financial Studies， 2010， 23（1）：147-168.

[16] 杨宏林，滑淑美，陈收.融资融券对股市特质波动率影响的实证研究[J].上海金融，2016，（1）：73-77.

[17] 戴方哲，尹力博.证券分析师“变脸”行为会增加股票特质波动率吗？[J].管理评论，2017，（5）：14-22+130.

[18] 叶建华.“热手效应”和“赌徒谬误”决策偏差与股市极大日收益率异象——基于中国A股市场的经验证据[J].管理评论，2016，（11）：30-39.

[19] Delong， B.， Shleifer， A.， Summers， L.H， et al.Noise Trader Risk in Financial Market[J].Journal of Political Economy， 1990， 98（4）： 703-738.

[20] Shleifer， A.， Vishny， R.W.The Limits of Arbitrage[J].The Journal of Finance， 1997， 52（1）：35-55.

[21] Stambaugh，R.F.， Yu，J.， Yuan， Y.Arbitrage Asymmetry and the Idiosyncratic Volatility Puzzle[J].The Journal of Finance， 2015， 70（5）：1903-1948.