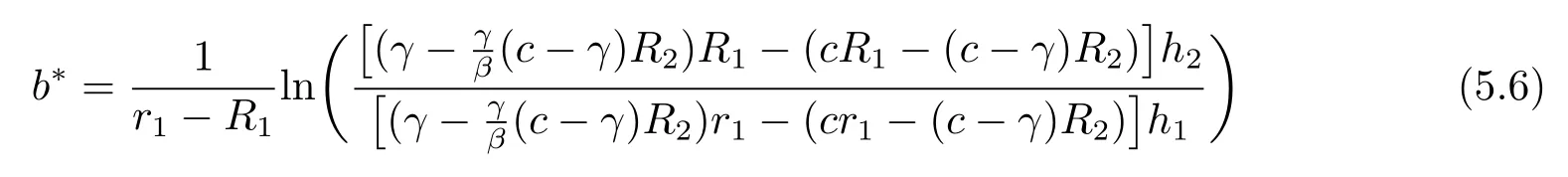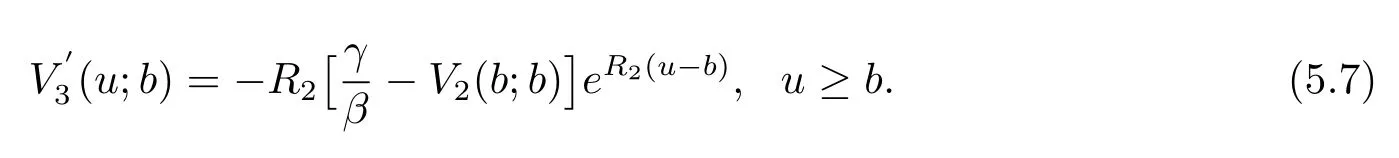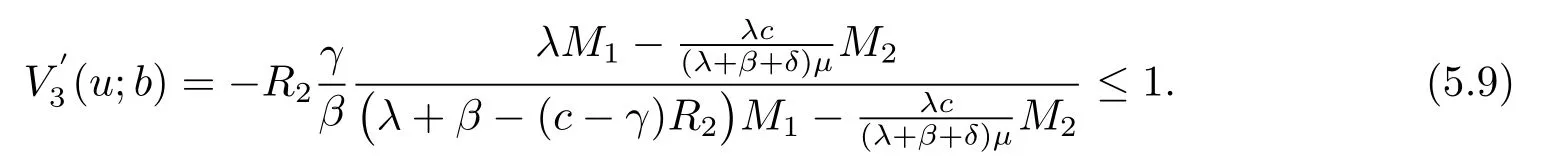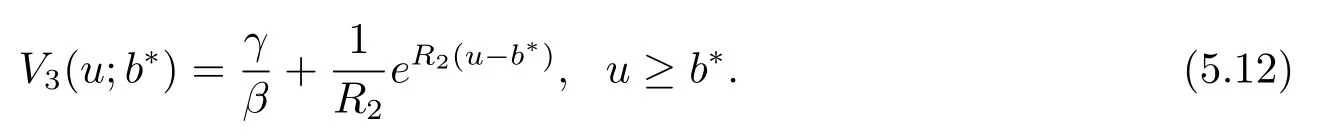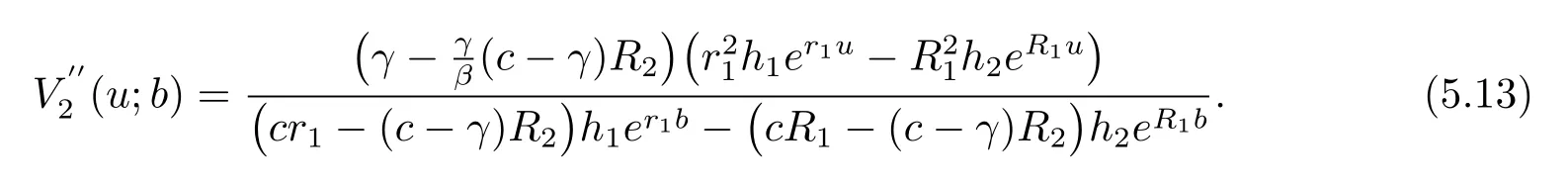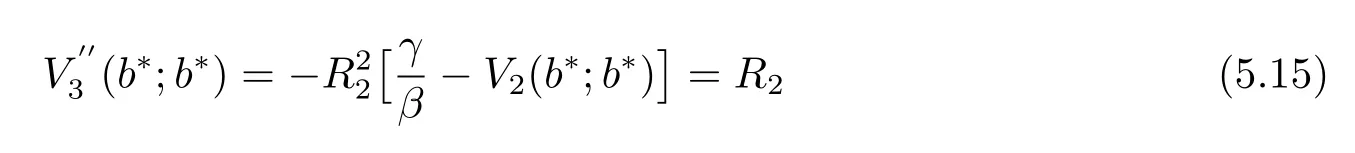OPTIMAL DIVIDEND STRATEGIES FOR THE COMPOUND POISSON MODEL WITH DEBIT INTEREST
2019-11-23LUOKuiLIUJuanZHAOYihuiXIAOLiqun
LUO Kui, LIU Juan, ZHAO Yi-hui, XIAO Li-qun
(1.Industrial Training Centre, Shenzhen Polytechnic, Shenzhen 518055, China)
(2.School of Mathematics and Statistics, Guangdong University of Finance and Economic,Guangzhou 510320, China)
(3.School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018, China)
(4.School of Economics and Statistics, Guangzhou University, Guangzhou 510006, China)
Abstract: In this paper, we study the optimal dividend strategy for an insurance company with debit interest and dividend payments.By HJB methods, a rule for choosing the strategy that maximizes the expected accumulated discounted dividends until absolute ruin is given.Under the so called threshold strategy, we derive integro-differential equations for the expected accumulated discounted dividends until absolute ruin.Then, explicit expressions for the expected accumulated discounted dividends until absolute ruin with exponential claim amounts are obtained.Finally,based on the explicit expressions, we prove that the optimal strategy is a threshold strategy and the optimal level of threshold is also obtained.
Keywords: debit interest; threshold dividend strategy; optimal strategy; the expected discounted penalty function
1 Introduction
Let {R(t)=x+ct−S(t),t≥0} be the compound Poisson surplus process for an insurer, wherex≥0 is the initial surplus,c> 0 is the gross premium rate, the aggregate claims process {S(t),t≥0} is a compound Poisson process with claim frequencyλand i.i.d.nonnegative random variables with a common distribution functionF(y) that satisfiesF(0)=0 and has a finite meanµ.
Generally, when the surplus ever drops below zero we say that the insurer is at ruin.In reality, however, when the surplus is negative, the insurer could borrow an amount of money that equals to the deficit at a debit rate interest forceδ>0 to continue her business.Meanwhile,the insurer will repay the debts continuously from her premium.Thus the surplus of the insurer is driven under the interest forceδwhen the surplus is negative.The negative surplus may return to a positive level.It is clear that when the negative surplus attains or is below the level −c/δ, the surplus is no longer able to be positive and consequently absolute ruin occurs at that moment.
We denote the compound Poisson surplus process with debit interest forceδbyRδ(t),which satisfies the following differential equation
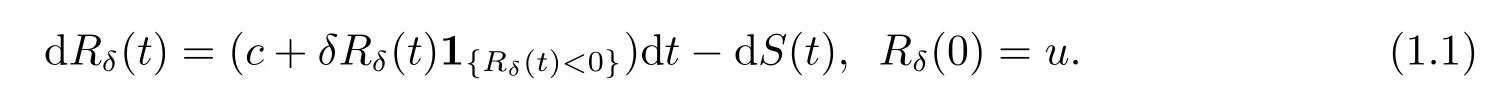
In literature, model (1.1) is discussed by Zhou and Zhang [1], Cai [2], and among others.
We now enrich model(1.1).We assume that the insurance company is a stock company,and dividends are paid to the shareholders according to a certain dividend strategyL.LetD(t) denote the accumulated paid dividends up to timet, and {Uδ(t),t≥0} be the company’s surplus.Thus

In addition,it is reasonable to assume that no dividends should be paid out when the surplus below zero.Now, we define the absolute ruin time byτδ=inf{t≥0 :Uδ(t)≤0} and the present value of all dividends until absolute ruin bywhereβ>0 is the force of interest for valuation.The performance of the strategyL={D(t)}t≥0is measured by the expectation of the present value of all dividends until absolute ruin, that is

In literature,V(u;L) is also said to be the value function associated to a strategyL.Under the criterion of maximizing the value functionV(u;L),the company usually wants to choose an optimal dividend strategy which is denoted byL∗.A dividend strategyL∗is said to be optimal if and only if

where the supremum is taken over the set Π of all admissible strategies.
The optimal dividend problem goes back to De Finetti [3], who found that the optimal strategy must be a barrier strategy and showed how the optimal level of the barrier can be determined.A first treatment of the optimal dividend strategy in the compound Poisson surplus process can be found in Section 6.4 of Bhlmann [4].The problem of finding the optimal dividend payment strategy was discussed extensively by Borch [5, 6], Zhao et al.[7], Thonhausera and Albrechera [8].Moreover, Gerber and Shiu [9]considered the optimal dividend strategies in the compound Poisson model.They showed that the maximal value function of the dividends can be characterized by the Hamilton-Jacobi-Bellman(HJB)equation.A rule for deciding between plowback and dividend payout is derived.Some recent papers on the compound Poisson risk model with debit interest and dividend payments are Yuan and Hu [10], Yuen et al.[11]and so on.
In this paper, we study this optimization problem under model(1.2)and the constraint that only dividend strategies with dividend rate bounded by a ceiling are admissible.We assume that the ceiling is less than the premium rate.Thus, the constraint is dD(t)≤γdt,whereγ∈(0,c)is the dividend-rate ceiling.The theoretical foundations are laid in Section 2.It is shown that the maximal value function can be characterized by the Hamilton-Jacobi-Bellman (HJB) equation.A rule for deciding between plowback and dividend payout is derived.Section 3 and Section 4 discuss the expectation of the discounted dividends until absolute ruin of a threshold strategy, if a threshold strategy is applied.Explicit expression of the value functionV(u;b) is given in the case of exponential claim amount distributions.In Section 5, for the case of an exponential claim amount distribution, it is shown that the optimal dividend strategy is a threshold strategy, and the optimal threshold is determined.
2 The HJB Equation and Verification of Optimality
In this section, we first show that the expectation of the present value of all dividends of an optimal strategy satisfies Bellman’s dynamic programming principle.And then show that if the value function associated to a strategyL,V(u;L) satisfying the HJB equation,it is indeed an optimal strategy.
LetB(u,0)=E[e−βT(u,0)]denote the Laplace transform ofT(u,0), whereT(u,0) is the first passage time from a given surplus levelu(−c/δ Foru≥0, consider the infinitesimal time interval (0,∆t], ∆t> 0, and the following dividend strategy.Suppose that between the time 0 and time ∆t, dividends are paid at rater, and thereafter, an optimal strategy is applied.By conditioning on whether there is a claim in this time interval and on the amount of the claim if it occurs, we see that the expectation of the present value of all dividends until absolute ruin is Taylor expansion yields that We maximum the value of (2.1) forr∈[0,γ].Then, the fact thatm(u) is the optimal value shows thatm(u) satisfies the HJB functional equation Conversely, for some given dividend strategy, letv(u)=E[D], a function of the initial surplusu≥0, ifv(u) satisfies the HJB equation (2.2), by a similar argument to Section 4 in Gerber and Shiu [9], we know that the given strategy is an optimal dividend strategy. From (2.2), we know that the expression to be maximized isthus, the optimal dividend rate at time 0 is If the solution of equation(2.2)has the property thatforu Threshold strategy are of interest, even in cases where the optimal dividend strategy is not of this form.LetLbe the threshold strategy, then model (1.2) can be described as withUδ(0)=u.LetV(u;b) denote the expectation of the present value of all dividend until absolute ruin, whereuis the initial surplus andbis the threshold.Note that the path ofV(u;b) is different at −c/δ In the following theorem, we derive integro-differential equations forV(u;b). Theorem 3.1As a function ofu, the expected discounted value of all dividends until ruinV(u;b) satisfies the following integro-differential equations for −c/δ for 0≤u ProofFor −c/δ wherehδ(t,u)=ueδt+c(eδt−1)/δ<0 is the surplus at time ∆tif no claim occurs during(0,∆t].The Taylor expansion yields SubtractingV1(u;b) from both sides of the above equation, dividing by ∆tand then letting∆t→0, we achieve (3.1).Similarly, one can obtain (3.2) and (3.3).This completes the proof of Theorem 3.1. We mentioned that,in the case whenγ=c,Theorem 3.1 above then reduces to Theorem 2.1 in Yuen et al.[11]. Proposition 3.1The boundary conditions ofV(u;b) are as follows. Moreover, by the continuous assumption, we have ProofCondition (3.4) is obviously for the fact that whenUδ(0)=−c/δthe surplus stays at the zero until the next claim and at this time ruin occurs.Whenu→∞, then the ruin timeτδ=∞, and thenwhich leads to (3.5).The proof of Proposition 3.1 is completed. In this section, we will calculate the explicit expressions ofV(u;b) with the assumption that the claim size is exponentially distributed with meanµ. SubstitutingF(y)=1−e−y/µinto(3.1)–(3.3),respectively,and changing the integration variables, we get for −c/δ for 0≤u foru≥b.Applying the operatorrespectively, we have for −c/δ for 0≤u foru≥b. When −c/δ By eq.(13.1.15)and eq.(13.1.18)of Abranmowitz and Stegun[12],we know that the solution of (4.7) has the form whereU(a,b;x) andM(a,b;x) are the confluent hypergeometric function of the first and second kinds, respectively, andc0andc1are unknown constants to be determined.From the boundary condition (3.4) we know thatc0=0.Hence When 0≤u wherec2andc3are unknown constants to be determined, andr1> 0R1< 0 are the roots of the equationcr2−(λ+β−c/µ)r−β/µ=0. Whenu≥b, Condition (3.5) shows that the solution of (4.6) is of the form By the boundary conditions (3.6)–(3.8), we have By solving the above equations, we obtain Now, if we assume that the optimal strategy is a threshold strategy and letb∗denote the optimal threshold.We first assume thatb∗>0, (2.3) implies that If then one can chooseb∗=0.Thus,the threshold strategy withb∗=0 is the optimal strategy. From the boundary conditions (5.4) or (5.5) we can obtain the optimal threshold valueb∗. Next, we show that for an exponential claim amount, the optimal dividend strategy is indeed a threshold strategy. Theorem 5.1For an exponential claim distribution, the threshold dividend strategy with is the optimal strategy in model (1.2). ProofFrom (4.13), it follows that Thus,b∗=0 if condition (5.3) is satisfied or, equivalently, if which by (4.12) is Now, suppose that the inequalities in (5.8) and (5.9) are changed from≤to >.From(5.5) and (5.7), we get the condition forb∗, that is,b∗is the solution of the equation From this and (4.13), it follows that It remains to verify conditions (5.2) and (5.3) are satisfied.Condition (5.3) is trivial from(5.10).Note that differentiating (4.12) twice yields The eq.(3.5) in Yuen et al.[11]shows thath1andh2have the same sign.It is trivial thatM1> 0,M2> 0, andThen (5.13) is an increasing function because it is the difference of an increasing and a decreasing function; hence its maximum value for 0≤u From (4.5) and (5.4), we have and from (4.6) and (5.5), we have Hence (5.14) is the same as the condition thatwhich is certainly true because by (5.11). Finally, we determine the value ofb∗by solving (5.4) or (5.5).This leads to (5.6).We complete the proof of Theorem 5.1.


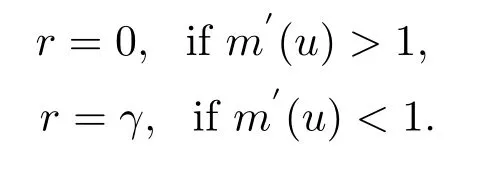

3 Threshold Strategy

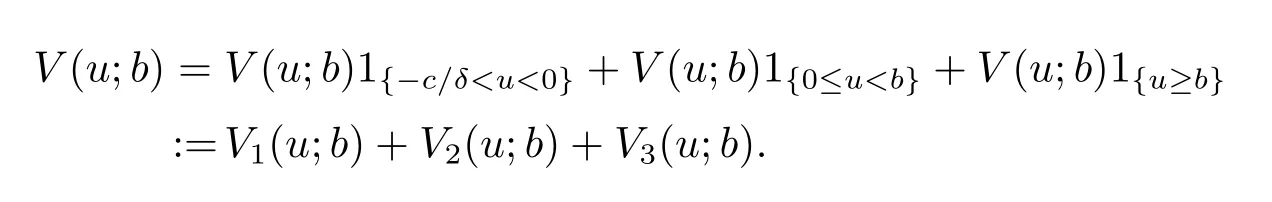

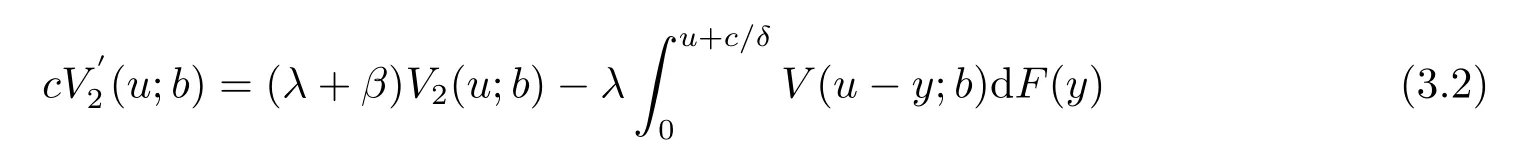

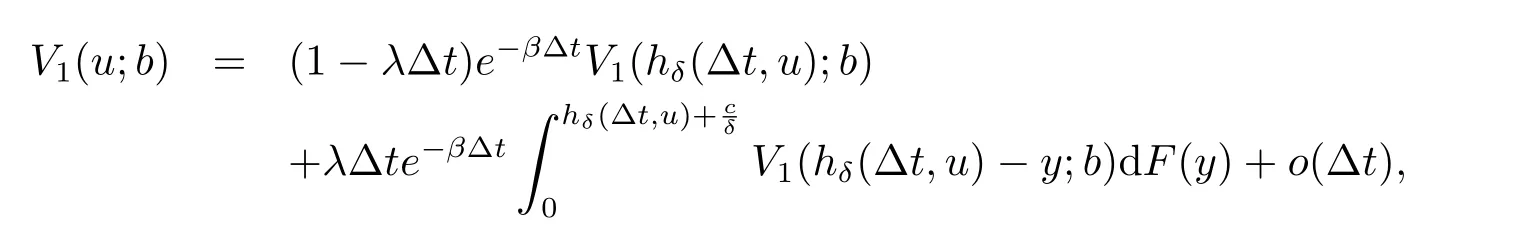


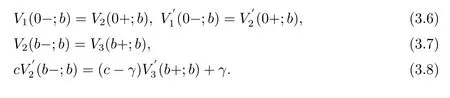
4 Analysis of V(u;b) with Exponential Claim


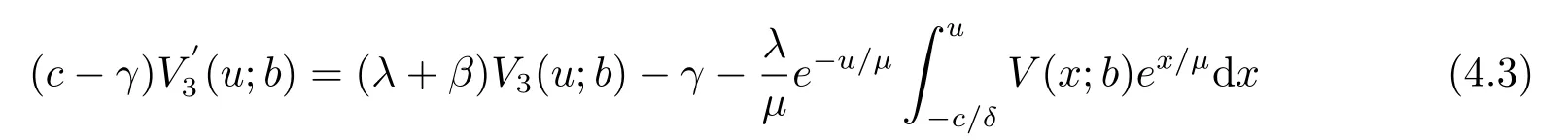
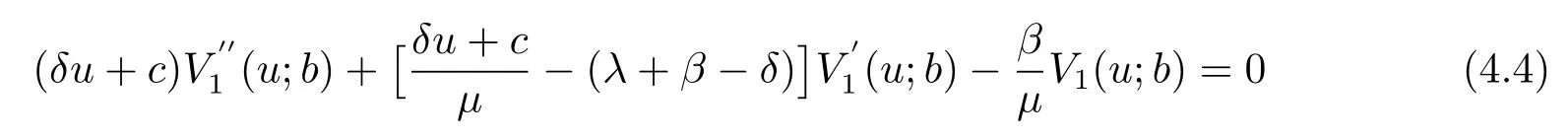

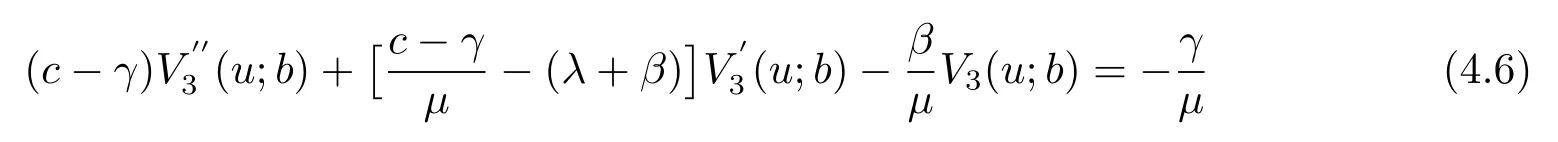
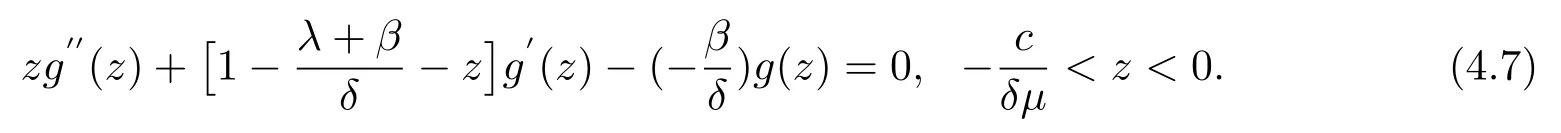




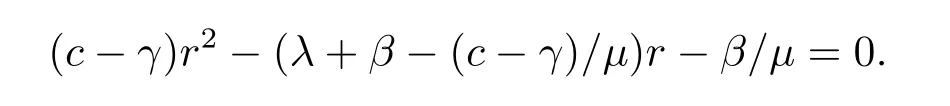
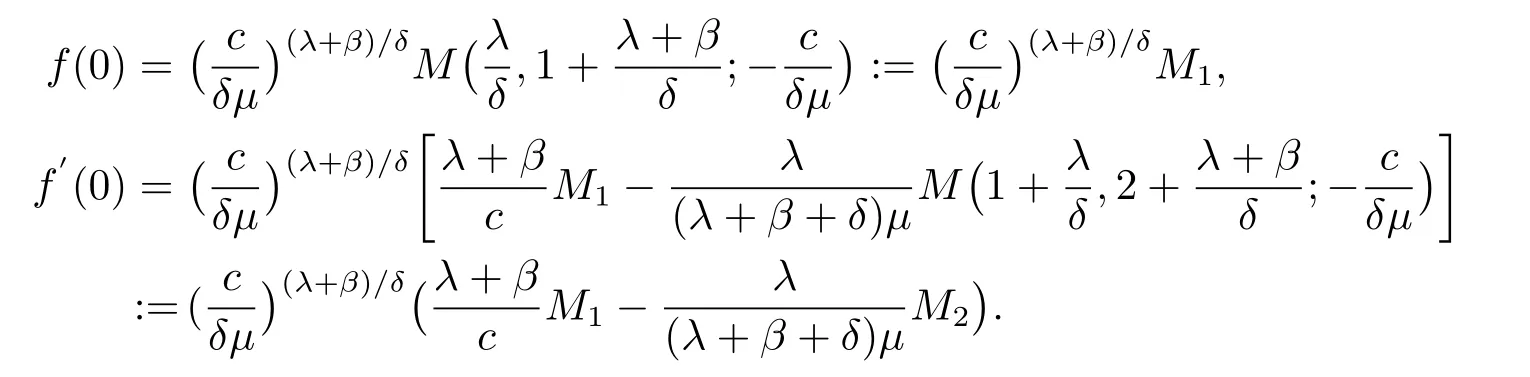


5 Optimal Threshold Strategies