基于RSSI滤波的三边室内定位算法
2019-11-22程俊


摘 要:针对复杂的室内环境中,基于接收信号强度指示(RSSI)定位困难的问题,提出了一种基于卡尔曼滤波、高斯滤波、统计中值相结合(KGSM滤波)的三边测距定位算法。算法先用KGSM滤波优化了RSSI值,然后运用对数损耗模型计算出距离,最后用三边测距得到了定位位置。实验结果表明:KGSM滤波提高了采集的RSSI值精确度,使三边定位算法的定位误差维持在0.7~1.0m,提高了定位的稳定性和精确度。
关键词:接收信号强度指示;室内定位;滤波方式;三边测距;定位误差
中图分类号:TP393 文献标识码:A
现实生活中,GPS已广泛用于室外定位,但在室内环境中,由于建筑物的阻挡,GPS定位无法开展。为了解决上述问题,人们尝试引入其他方法来实现定位。目前,常用于室内定位的方法可以分为测距和非测距两类,测距算法包括TOA、TDOA、RSSI、AOA等,非测距算法包括APIT、凸规划法、质心法、DV-Hop等方法。基于测距的RSSI算法应用广泛,但是其易受各种各样环境的影响,故人们常常对其进行滤波处理。常用的RSSI滤波方法有均值濾波、高斯滤波、中值滤波、卡尔曼滤波以及它们的融合等。文章[1]对高斯滤波进行了改进,其更符合理论模型,滤波效果更好。文章[2]将卡尔曼滤波和中值滤波进行了结合,有效减少了粗大RSSI值对结果的影响。受上述相关文献的启发,本文融合了卡尔曼滤波、高斯滤波、中值滤波的改进型统计中值滤波的优点,提出了一种新型滤波—KGSM(Kalman,Gaussian and Statistics median)滤波,提高了其精确度,进而减少了三边定位算法的[3]的定位误差。
1 KGSM滤波优化RSSI值
1.1 传统滤波方法分析
室内定位中,由于存在人员走动、信号的反射、电子仪器本身的干扰等不稳定因素,使接收的RSSI值存在很大的误差,为了提高其精确度,我们常常对其进行滤波处理,这里我们简单介绍下本论文用到的滤波:中值滤波、高斯滤波、卡尔曼滤波。中值滤波对采样信号取中间值,它能有效克服因偶然因数引起的波动干扰,但对于脉冲干扰比较强、样本容量不多的情况下,滤波效果不理想;高斯滤波可以解决RSSI在实际测试中易受干扰、稳定性差等问题,但对于阴影效应、电子仪器本身干扰等长时间干扰问题处理效果欠佳;卡尔曼滤波能去除叠加在信号上的加性噪声,平滑显著误差,但却无法去除误差,若末尾几个测量值误差大,将对结果会有重大影响。
1.2 KGSM滤波
本文采用混合滤波的方法,将卡尔曼滤波、高斯滤波、中值滤波的改进型统计中值滤波相结合,提出了KGSM滤波。其具体算法如下:
(1)某个时间段内对RSSI信号采集N(N100)次,用卡尔曼滤波对每个采样值进行迭代,使由于仪器等产生的噪声干扰得到减少,并平滑了显著误差。但是由于卡尔曼滤波存在数据惯性的累积,当前一时刻采样值波动越大,它的下一时刻滤波值也波动越大,同时,如果这种波动存在采样值的末端,将对最后的RSSI滤波值产生重大影响。
(2)收集每一个采样值对应的卡尔曼滤波值,对其进行高斯滤波取值,留下中间大概70%左右的滤波值。该步骤剔除了偏离真实值较大的一部分卡尔曼滤波值,可以很大程度解决末尾几个RSSI采样值波动对滤波结果的影响。
(3)由于本实验是在一个相对复杂的室内环境进行,经过高斯滤波取值后,仍然存在很多偏离真实值的滤波值,为了提高RSSI精确度,以免影响接下来三边测距定位算法的估算。在高斯滤波取值后,我们对其进行了统计中值滤波,大致步骤为如下三步:
①对高斯取值后的RSSI信号从小到大排序,得到RSSIi(i=1,2,…),中值滤波取得中间值RSSImid。
②将各个信号值与中值的偏差平方均值作为阈值T,当偏差平方大于阈值时,权值由偏差平方决定,反之则由阈值决定,这种设计相比于传统的中值滤波,对于高斯滤波取值仍然存在很多偏离真实值的情况,有更好的滤波效果。这里我们设排序后第i个值所占的权重ωi:
ωi=11+max{T,(RSSIi-RSSImid)2}∑Ni=111+max{T,(RSSIi-RSSImid)2}(1)
其中:T=∑Ni=1(RSSIi-RSSImid)2/N
③将高斯取值后的值与其加权系数相乘,得到最终的统计中值滤波值,也就是KGSM滤波值:
RSSIKGSM=∑Ni=1ωi*RSSIi(2)
2 基于三边测距的定位算法
KGSM滤波后得RSSIKGSM,然后采用对数损耗模型,通过计算,得到相应的距离。在室内,我们布置了三个AP:AP1,AP2,AP3,坐标为(x1,y1),(x2,y2),(x3,y3),定位位置D(x,y)离三个AP的距离为di(i=1,2,3),以AP1,AP2,AP3 为圆心,d1,d2,d3为半径分别画三个圆。
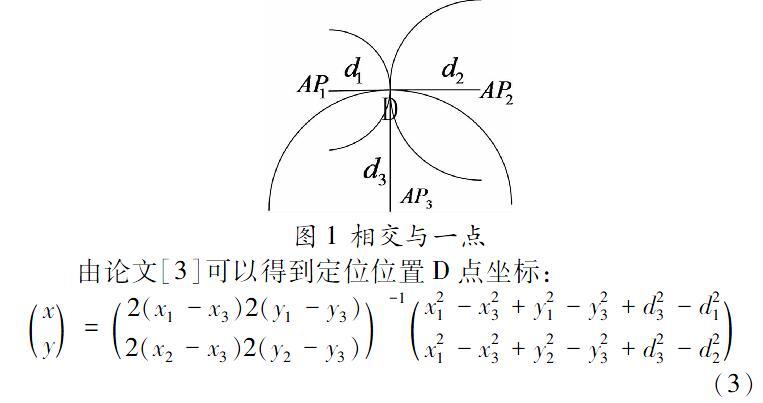
(1)运用三边测距算得三个圆交于一点,如图1所示:
由论文[3]可以得到定位位置D点坐标:
x
y=2(x1-x3)2(y1-y3)
2(x2-x3)2(y2-y3)-1x21-x23+y21-y23+d23-d21
x21-x23+y22-y23+d23-d22
(3)
3 实验结果与分析
室内定位中,人员走动会等突发干扰,可能引起RSSI值偏离真实值较大,带来显著误差;信号反射、电子仪器本身干扰等随机干扰,会使采样值围绕真实值上下波动,带来随机误差。而相对复杂的室内环境中可能存在着大量的突发干扰和随机干扰。为了验证该KGSM滤波算法的定位性能。设计实验环境如下:室内大小为10m×10m,存在频繁的人员走动,空间中布置了3个AP,在定位位置,我们用采样频率为5次/s的手机采集信号,一段连续时间内,采集了每个AP的200次RSSI值,改变定位位置,重复上述实验10次,获得10组不同的数据。
选取RSSI样本的标准差σs作为定位性
能的判定,其公式表示如下:
σs=1N-1∑Ni=1(RSSIi-RSSI)2(4)
其中:RSSI为真实值,RSSIi采样点上滤波值。
图2比较了高斯滤波、卡尔曼滤波、统计中值滤波、KGSM滤波对RSSI的滤波性能,图3比较了基于四种滤波算法的定位误差。由图2、图3可以发现:(1)复杂的室内环境中,由于信号长期受到干扰,采样值经过高斯滤波取值后,信号波动还是比较大,表现为高斯滤波的样本标准差σs 整体上最大,基于高斯滤波的定位误差整体上也相对较大。(2)由图2实验序号1、2、3、8、10可看出,卡爾曼滤波模型在突发干扰引起的显著误差不多时,其滤波性能优于统计中值模型;由图2剩余实验序号可以看出,当显著误差较多时,由于卡尔曼滤波只能平滑显著误差,无法去除,其去除显著误差的能力不如统计中值模型。如图3实验序号6、8可以看出,当末尾几个采样值出现较大波动时,卡尔曼滤波其定位效果将受重大影响;(3)KGSM滤波的σs整体上最小,产生的定位误差也最小、最稳定,误差稳定在0.7~1.0m,这也就证明了基于RSSI的KGSM滤波的能提高三边定位算法的精确度和稳定性。
综上所述,KGSM滤波先运用卡尔曼滤波平滑了各种干扰引起的误差,然后通过高斯滤波取值去除卡尔曼滤波后的相对显著误差,最后运用改进的中值滤波—统计中值滤波,进一步平滑了随机误差,提高了RSSI值的精确度,使三边测距后的误差稳定在0.7~1.0m,有效的提高了定位的精确度和稳定性。
4 结语
本文针对复杂的室内环境,在研究各种滤波算法优缺点的基础上,提出了一种新的滤波:KGSM滤波。该滤波相比于传统滤波,优化了RSSI值。然后通过对数损耗模型将滤波后的RSSI值转化为距离,运用三边测距算法得到了定位位置。实验表明:运用KGSM滤波后进行的三边定位算法的定位误差为0.7~1m,提高了定位的精确度和稳定性。虽然基于KGSM滤波的三边定位算法提高了定位精度,但仍存在一定的局限,以后可以从以下几个方向进行改进:(1)KGSM滤波融合了三种滤波,增加了算法复杂性,下一步工作将寻找某种或几种滤波,使得RSSI值精确度提高的同时,算法复杂度也减小;(2)进行三边测距定位算法得到的位置是个准确值,实际上由于室内环境复杂,最终可能导致三个圆不相交与一点。
参考文献:
[1]陈丽,王学东,孙晶晶.基于改进高斯滤波的室内无线定位算法[J].电气自动化,2014,36(3):31-33.
[2]刘鋆.基于卡尔曼滤波的WSNs定位系统研究与设计[D].华中师范大学,2014.
[3]廖兴宇,余敏,汪伦杰.基于锚球交域投影质心的WSNs三维定位算法[J].传感器与微系统,2014,33(6):126-128.
作者简介:程俊(1989-),男,汉族,硕士研究生,主研方向:物联网、无线传感网。
