3-RPS并联机器人动力学分析及模糊控制仿真

严智敏，徐顺建，简辉华

(新余学院 机电工程学院，江西 新余 338004)

0 引 言

目前，随着机器人技术的快速发展，并联机器人因精度高、 承载能力强、 刚度大等优点，被广泛应用于众多工业生产中，并且在勘探、 医学、 武器系统等诸多领域中也发挥了非常重要的作用[1]. 但由于并联机器人结构系统非常复杂，具有强耦合、 非线性的特点，导致其控制不便，严重影响了并联机器人的控制精度，而与并联机器人控制有最直接关系的是动力学方程的建立[2].

机构动力学研究的是机构运动与力之间的关系，范围很广，主要包括分析构件之间的相互受力关系、 利用机构的运动学分析进行机构的动力学建模、 计算机构的惯性力及动态仿真等[3]. 只有系统地分析机构在某种运动下与构件之间产生的力的相互关系，如不同的力对应机构不同的运动状态，才能更好地对机构进行有效的实时控制[4]. 其中建立数学模型，用数学函数模型代替机构模型作为控制对象，是实现并联机器人控制的基础. 数学模型越精确，对应的控制精度也越高[5]. 动力学模型的优劣直接反映出并联机器人控制精度的高低. 对于同一机构，不同的建模方法对机构控制的作用效果也会有很大的差异[6]. 近年来，国内外学者对并联机器人进行动力学建模的方法主要包括：拉格朗日法(Lagrange)、 牛顿-欧拉法(Newton-Euler)、 虚功原理法、 高斯法(Gauss)等[7]. 本文应用牛顿-欧拉法对3-RPS型并联机器人进行动力学分析，得出该并联机器人的驱动力、 约束力矩以及动平台对支链的作用力，建立动力学方程，在此基础上，应用Matlab构建仿真模型进行仿真分析，验证其精度及方法的正确性，为研究3-RPS并联机器人驱动位移轨迹跟踪控制作铺垫.

1 机构描述

3-RPS并联机构示意图如图 1 所示，该机构由上下两平台、 3支链连接组成，每条支链包涵三个运动副：转动副、 移动副、 球副. 转动副与固定平台相联，球副与动平台相联，中间通过移动副连接，该机构的驱动副为移动副.

图 1 3-RPS机构示意图Fig.1 Schematic diagram of 3-RPS mechanism

建立坐标系，上平台建立动坐标系P-UVW，下平台建立固定坐标系O-XYZ，P，O分别为上下平台的中心. 建立支链坐标系Ai-xiyizi，z轴方向为杆长的方向，x轴方向为OAi的延长线方向，y轴方向由右手定则确定. 上下平台分别记为B1B2B3，A1A2A3，其中，PBi,OAi,OBi分别记为bi,ai,qi，di表示驱动杆AiBi之间的杆长，φi为连杆AiBi与下平台之间的倾斜角，θi为转动副轴线ui与X轴之间的夹角，L为上平台三角形的边长.

2 逆运动学分析

2.1 位置分析

根据图 2 支链结构示意图，有如下关系式

ai+disi=P+bi,

(1)

式中：si表示在定坐标下zi轴的单位向量.

图 2 支链示意图Fig.2 Schematic diagram of the branch

则有

di=‖P+bi-ai‖,

(2)

si=(P+bi-ai)/di.

(3)

在固定坐标系中，支链固定杆和驱动杆质心的位置矢量分别为

r1i=ai+e1si,

(4)

r2i=ai+(di-e2)si,

(5)

式中：e1,e2如图 2 所示.

取欧拉角Z-Y-X型[8]，α=0，则动坐标系相对于固定坐标系的方向余弦矩阵为

(6)

则动平台的角速度为

(7)

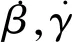
由图 1 可知，固定坐标系经两次旋转变换可得到支链坐标系Ai-xiyizi, 先绕Z轴旋转φi角，再绕新形成的Y1轴旋转ηi角，则支链坐标系相对固定坐标系的变换矩阵为[9]

(8)

由于转动副的约束作用，支链只能在xizi平面内转动，转轴为yi，则有φi为定值，且φ1=0，φ2=60°，φ3=120°. 由坐标变换有

(9)

2.2 速度和加速度分析

式(1)右边对时间求导得固定坐标系下球副中心Bi的速度为

vBi=vp+wp×bi.

(10)

由于vBi=ARiivBi，则有

ivBi=iRAvBi,

(11)

式中：ivBi表示Bi在Ai-xiyizi坐标系下的速度.

式(1)左边对时间求导得

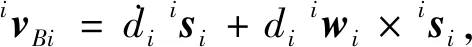
(12)

式中：iwi,isi分别表示在Ai-xiyizi坐标系下支链的角速度和zi轴的单位向量.

对式(12)两边做向量运算并化简，可得

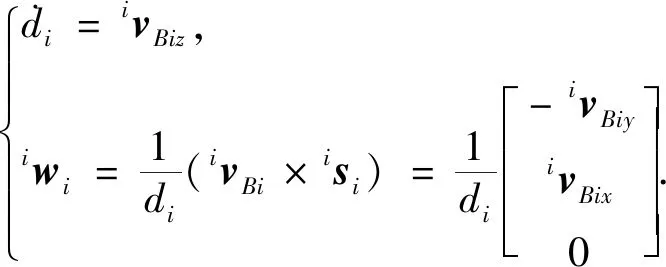
(13)

由于支链只能绕yi轴转动，则ivBi在yi轴上的分量为零，即ivBiy=0.

式(4)，式(5)分别对时间求导，并依据上述所求得的值化简可得，在Ai-xiyizi坐标系下支链固定杆和驱动杆质心的速度

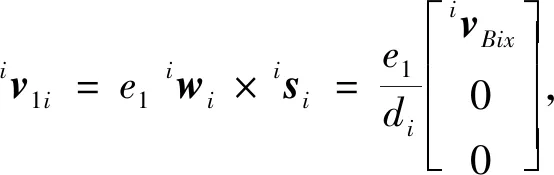
(14)

(15)

式中：ivBix，ivBiy，ivBiz分别表示ivBi在xi，yi，zi轴上的分量.

再对式(10)求导可得固定坐标系下球副中心Bi的加速度

(16)

且有

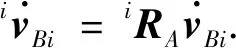
(17)

对式(12)求导同样也有

(18)

同理对式(18)两边做向量运算并化简得

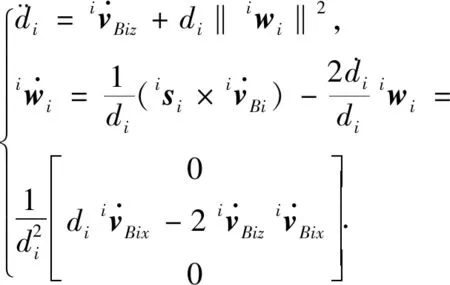
(19)

式(14)，式(15)分别对时间求导，并依据上述所求得的值化简可得，Ai-xiyizi坐标系下支链固定杆和驱动杆质心的加速度

(20)

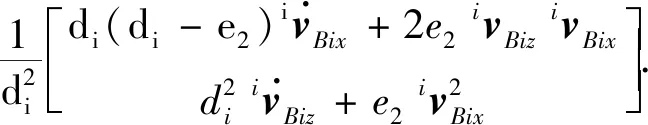
(21)

3 动力学方程的建立

以动平台为研究对象，在动坐标系下，根据牛顿-欧拉方程可得动平台的力矩平衡方程[10]

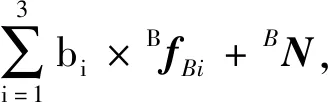
(22)

动平台的力平衡方程[11]为

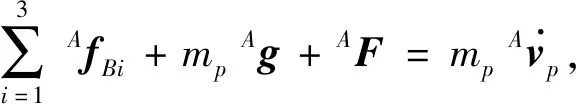
(23)

假设ifBi表示在支链坐标系下动平台对支链的作用力，则固定坐标系下和动坐标系下该支链作用于动平台上的力分别为

AfBi=ARiifBi,

(24)

BfBi=BRAAfBi=-BRiifBi.

(25)

联立式(6), (8), (22), (24)和(25)，由于动平台关于其质心的惯性积为零，且Ipu=Ipv，则有

(26)

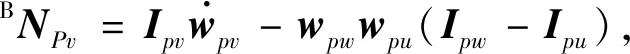
(27)

biv(a11ifBix+a12ifBiy+a13ifBiz)]+BNPw=

(28)

式中：右下标中的u，v，w分别表示该量在动坐标系下U，V，W轴上的分量；Ip表示动平台对于其质心的主惯性矩；Bwp=[wpuwpvwpw]表示动坐标系下动平台的角速度矢量.

联立式(6), (8), (23), (24)和(25)可得

ifBizcosφisinηi)+AFx=0,

(29)

ifBizsinφisinηi)+AFy=0,

(30)

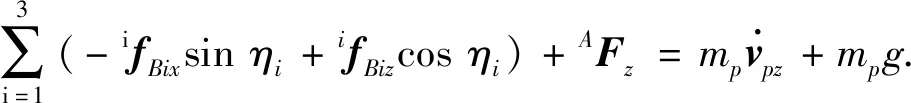
(31)

联立式(26)～(31)可求得ifBiy，ifBiz，根据机构力平衡关系，则有3-RPS并联机器人所需的驱动力和约束力矩分别为

(32)

Mi=iMAix=diifBiy,

(33)

式中：iMAix表示在Ai-xiyizi坐标系下动平台作用于该支链下的约束力矩在xi轴上的分量.

以支链为研究对象，在支链坐标系下，根据牛顿-欧拉方程有[12]

(34)

式中：inAi，ihAi分别表示在支链坐标系下作用于Ai点的合外力矩和该支链关于Ai点的合角动量.

inAi=diisi×(-ifBi)+[m1e1+m2(di-

e2)](isi×iRAAg)+iMAi,

(35)

ihAi=m1e1(isi×iv1i)+m2(di-e2)(is1×iv2i)+

iI1iiwi+iI2iiwi,

(36)

式中：iI1i，iI2i分别表示支链固定杆和驱动杆关于各质心的转动惯量.

式(36)对时间求导得

(iI2iiwi).

(37)

联立式(34), (35)和(37)得

(38)

式中：I1iy，I2iy分别表示支链固定杆和驱动杆关于各自质心的主惯性矩在yi轴上的分量.

从而求得动平台对支链的作用力ifBi=[ifBixifBiyifbiz]T.

4 模糊控制仿真分析

为了满足该机构能够实现高精度、 快速响应、 结构紧凑的运动特点，综合各方面的因素[13]，考虑机构实现的是直线运动，对于3-RPS型并联机器人，选择液压伺服驱动作为驱动器，采用液压伺服系统的闭环传递函数[14]

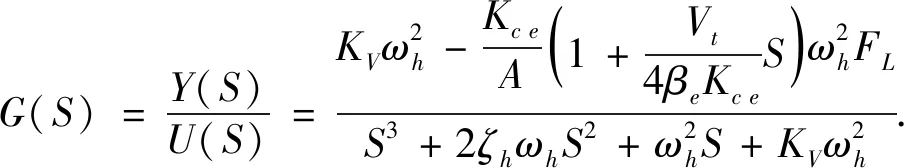
(39)

给定驱动器的参数：KV=0.06，ωh=320，δh=0.2，Vt=1.4×10-4，KCE=6.14×10-12，βe=7×108，A1=4.9×10-4，Ft=1 000，将其代入传递函数中得

选用模糊控制方法[15]，应用Matlab软件建立控制模型进行仿真分析.

应用Matlab的FIS编辑器建立模糊控制器，构建模糊控制模型进行仿真，如图 3 所示.

经过多次仿真实验，调节量化因子ke,kec和比例因子ku，使其控制精度达到最佳状态时，ke=0.3×10-3，kec=0.2×10-7，ku=5×107. 仿真时间为10 s，仿真结果如图 4 所示.

仿真结果表明：采用模糊控制在轨迹跟踪控制中有一定的控制精度； 在系统一开始时就出现迅速响应，运行到0.2 s时就有一定的跟踪精度，并且跟踪的最大误差为1.1 mm，跟踪精度较高； 同时验证了采用牛顿-欧拉方法对3-RPS并联机器人动力学分析正确性.

图 3 模糊控制仿真模型Fig.3 Simulation model of fuzzy control

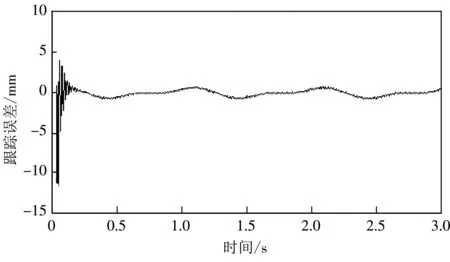
图 4 模糊控制轨迹跟踪误差Fig.4 Trajectory tracking error of fuzzy control

5 结 论

本文以3-RPS并联机器人的动平台以及各支链为研究对象，应用牛顿-欧拉方法，分析了该并联机器人支链杆件对动平台的驱动力、 约束力矩以及动平台对支链的作用力，构建了动力学方程. 基于Matlab仿真软件，采用液压伺服驱动方式及模糊控制算法，构建了模糊控制仿真模型来进行仿真分析，表明采用模糊控制在轨迹跟踪控制中有一定的控制精度，验证了采用牛顿-欧拉方法对3-RPS并联机器人动力学分析的正确性及控制方法的有效性，为进一步采用模糊PID控制、 滑膜控制等其它控制方法对3-RPS并联机器人轨迹跟踪控制研究，以及提高并联机器人控制精度提供一定的理论基础.