压电材料圆形板热弹耦合作用下的主共振

孟 莹，薛春霞，王 勋

(中北大学 理学院，山西 太原 030051)

0 引 言

近年来，压电材料由于其薄而轻、 响应速度快、 成本低、 寿命长、 转换效率高的优点受到了人们广泛的关注，被广泛应用于航天航空、 电子设备、 生物等领域[1]. 压电薄板是机械工程中应用十分广泛的一类构件. 在工程实际应用中，构件经常处于多种物理场环境中，例如温度场、 外激励、 磁场等，并表现出复杂的振动特性，这会严重影响构建运行的安全性. 因此研究温度场作用下的压电材料的动力学特性具有实际的工程意义. 许多研究学者对多物理场耦合作用下普通弹性材料及特殊功能材料进行了大量的分析[2-8]. 压电陶瓷复合材料的共振问题是一个经典的、 实用的工程问题，在实际中备受关注[9-10]. 徐榜等[11]研究了导电圆形薄板的磁弹性动力响应的问题基于电场-磁场-力场多场耦合理论. 薛春霞等[12]针对磁电弹性薄板，利用L-P方法得到薄板稳态下的幅频响应方程. 胡宇达等[13-14]对磁场环境中的旋转运动导电圆板轴对称振动问题进行了分析. 李林利等[15]运用弹性力学有限变形基本理论、 推导出在热弹耦合作用下压电双曲壳的非线性动力学方程，分析了温度场中的压电材料双曲壳发生混沌的非线性动力学行为.

综上所述，对于压电圆形薄板在热弹耦合作用下非线性动力学行为的分析还比较少，本文对处在温度场和外激励作用下的压电圆形薄板进行研究，利用弹性力学大挠度理论并结合Bubnov-Galerkin原理，求得压电圆形薄板非线性动力学方程. 并推导得出了系统的幅频、 相频响应方程及稳定性判别式. 通过数值算例，分析板中心温度、 机械载荷、 系统阻尼、 板厚等参数对系统非线性特性及稳态解的稳定性的影响.

1 压电圆形薄板的基本方程

薄板基本假设[16]：

1) 薄板假设：厚度h比其他两个方向小很多，法向应力可以忽略不计.

2) 动力学平衡方程中产生的应力和斜率的非线性项保留，这样可以考虑面内力的影响，而其他非线性项则可以忽略不计.

3) 板中初始状态垂直于中面的点变形后仍然垂直于中面，板的挠度主要和弯曲应变有关.

周边固支压电圆形薄板模型如图 1 所示.O为坐标原点,b为半径,h为薄板的厚度. 薄板上侧受简谐分布力q=q0cosωt, 其中,q0为外激励幅值，ω是激振频率. 材料性能是与温度无关的常数.

图 1 压电圆形薄板模型Fig.1 Circular thin plate model of piezoelectric material

对于横观各向同性的压电圆形薄板，考虑温度效应时的压电方程[17]为

(1)

式中：σr表示沿r方向上的正应力；σθ表示沿θ方向上的正应力；τr θ表示切应力；εr表示径向线应变；εθ表示环向线应变；γrθ表示切应变；cij(i,j=1,2,6)表示压电材料刚度；Dz表示电位移；Ez表示横向电场强度；T表示温度增量；ε33表示介电系数；e31表示压电系数；λ11=(c11+c12)α表示热-机械耦合系数[18]，α为热膨胀系数；m33表示热电耦合系数； 对于横观各向同性材料，c11=c12+2c66.

基于Von Karman大挠度理论，轴对称圆板的几何方程[19]为

(2)

由式(1)和式(2)得，中面力和内力矩为

(3)

压电圆形薄板运动方程[19]为

(4)

式中：Qr为剪力；ρ为材料密度；δ为阻尼系数.

引入应力函数φ:

(5)

将式(3)代入式(5)再结合式(4)，得到压电圆形薄板横向热振动方程

(6)

圆形薄板的轴对称应变协调方程[19]为

(7)

将εr,εθ用Nr,Nθ表示，结合式(5)，将其代入式(7)，可以得出压电圆形薄板热弹耦合振动协调方程为

(8)

式(6)和式(8)是基于弹性力学有限变形基本理论得到的热弹耦合作用下压电圆形薄板的非线性动力学方程. 如果不考虑圆形板的压电性，与文献[5]作对比，发现对于普通板仍然适用，因此验证了本文的结论的可靠性.

周边固支压电圆形薄板的边界条件为

(9)

横向位移设为

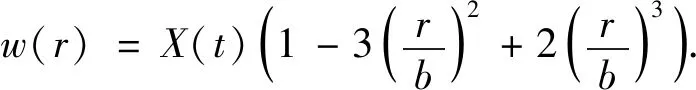
(10)

设板中的温度呈现抛物线分布，则

(11)

式中：T0为板中心温度；η≪1.

由式(11)得

(12)

基于薄板假设，压电圆形板很薄，面内电场可以被忽略. 只考虑横向电场Ez. 因此，

(13)

将式(10)，式(12)和式(13)代入式(8)，求得应力函数

(14)

将式(14)代入方程(6)，并对式(6)利用Bubnov-Galerkin原理可得

(15)

(16)

其中

2 主共振问题的多尺度法求解与稳定性分析

2.1 多尺度法求解主共振

为了研究系统的非线性主共振问题，使用多尺度法[21]对微分方程(16)进行求解，引入无量纲小参数ε，式(16)改写为

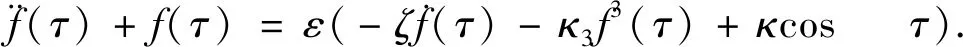
(17)

对于弱非线性系统，讨论一次近似解，令

f(τ,ε)=f0(Γ0,Γ1)+f1(Γ0,Γ1),

(18)

式中：Γn=εnτ为不同尺度的时间变量.

讨论系统的主共振情况，设

ϖ=1+εϑ,

(19)

式中：ϑ为调谐参数.

将式(18)和式(19)代入式(17)，展开后令两边ε0、ε1的同次幂项系数相等，可得

(20)

式中：D0=∂/∂Γ0;D1=∂/∂Γ1.

求解式(20)的第一式得

f0=acos(Γ0+φ),

(21)

式中：a=a(Γ0)；φ=φ(Γ1).

把式(21)代入式(20)的第二式，消除f1中的久期项得

(22)

式中：β=ϑΓ1-φ.

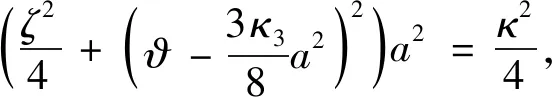
(23)

(24)

2.2 稳定性分析

为分析系统稳态运动的稳定性，引入扰动变量

a1=a-a0,β1=β-β0,

(25)

式中：ɑ0,β0为稳态运动下的稳态解. 把式(25)代入式(22)，经过泰勒展开，只保留ɑ1，β1的一次项，得到方程(22)在稳态值附近的一次近似方程

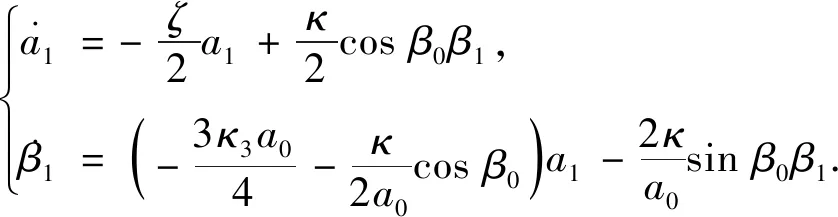
(26)

根据Lyapunov[22]一次近似解稳定性判据，由于ζ>0，则稳态解ɑ0,β0稳定的充要条件

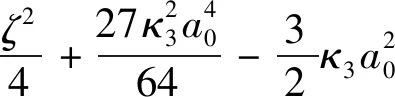
(27)

3 算例分析

针对温度场中受到外激励作用的压电圆形薄板进行数值分析. 选取压电材料为BaTiO3陶瓷. 圆板的半径b=600 mm，厚度h=10 mm. 材料具体参数如表 1 所示[23].

表 1 BaTiO3材料参数

图 2～图 5 分别给出了阻尼、 外激励幅值、 板中心温度、 厚度变化时系统的幅频特性曲线. 各图中实线代表稳定解，虚线代表不稳定解； 从图中可以看出：幅频特性曲线向左偏移，这是由于非线性项系数κ3<0，系统呈现软刚度特性及典型的非线性特性(包括多值性、 跳跃现象). 当外激励频率接近固有频率时，激起系统发生共振现象，即在ω/ω0=1的附近，振幅明显增大.

图 2 中其他参数q0=0.07 MPa，T0=40 ℃，η=0.1，ε=0.1. 由图 2 可以看出，当阻尼系数增大时，系统消耗的能量使系统的响应幅值减小以及发生跳跃的外激励频率与固有频率的比值减小，共振区域变化不明显.

图 3 中其他参数T0=40 ℃，η=0.1，ε=0.1，ζ=0.3. 从图 3 可以看出，当外激励幅值降低时，系统的振幅、 多值区间被抑制且共振区间也随之变窄. 发生跳跃时外激励频率与固有频率的比值增大.

图 2 阻尼变化时的幅频特性曲线Fig.2 Amplitude-frequency curves for different damping coefficients

图 3 外激励幅值变化时的幅频特性曲线Fig.3 Amplitude-frequency curves for different values of the amplitude of the external excitation

图 4 温度变化的幅频特性曲线Fig.4 Amplitude-frequency curves for different values of temperature

图 4 中其他参数q0=0.07 MPa，η=0.1，ζ=0.3，ε=0.1. 由图 4 可以看出，随着板中心温度的增大，系统的共振幅值逐渐减小，发生跳跃的外激励频率与固有频率的比值增大，板中心温度对系统的影响相当于阻尼的作用. 图 4(b)中以T0=40 ℃ 为例，具体分析了压电圆形薄板的跳跃现象. 在系统的响应中，压电椭圆形薄板存在的两个鞍节点分岔对应两次跳跃，分别为ω/ω0=0.86 和ω/ω0=0.94. 当ω/ω0从1.2开始缓慢减小时，系统的响应幅值随之增加，直到B点，即ω/ω0=0.86，在B点，系统响应突然跳跃到较小振幅的稳定分支上. 相反地，增大ω/ω0导致在另一点发生跳跃. 若ω/ω0从较小值开始缓慢增大，系统响应幅值沿曲线的下半分支增加到D点，即ω/ω0=0.94，此时系统的响应突然从低振幅D点跳跃到高振幅E点. 在ω/ω0<0.86或ω/ω0>0.94 时，系统出现一个响应幅值，在0.86<ω/ω0<0.94 时，系统出现3个响应幅值. 此时BD段所对应的区域为不稳定区域.

图 5 板厚变化时幅频特性曲线Fig.5 Amplitude-frequency curves of for different values of plate thickness

图 5 中其他参数q0=0.07 MPa，η=0.1，ζ=0.3，ε=0.1. 由图 5 可以看出，当板厚增大时，系统的响应幅值降低，共振区域变窄； 多解共存的区域也大大减小，系统的非线性软特性也逐渐减弱. 在实际操作中，在满足基本条件的基础上，选择适当的厚度具有非常高的经济意义.

图 6 为系统幅值随外激励幅值变化的响应曲线. 其他参数T0=40 ℃，η=0.1，ε=0.1. 如图所示：在q0<0.2 MPa，调谐参数ϑ=-1和-0.5时，幅频曲线出现3种解共存的现象，而调谐参数ϑ=0, 0.5, 1时，只有一个解. 在q0>0.2 MPa，无论调谐参数取何值，都只有一个解. 因此当ϑ<0时，较小的外激励容易引起系统出现不稳定区域，随着外激励幅值的增大，系统的响应幅值由多解共存变成了只有一个解的情形. 增大外激励幅值可以使系统避开多值区域，即不稳定区域. 当ϑ≥0时，不同的外激励幅值对应的响应幅值是唯一的. 当调谐参数越来越大，系统的幅值越来越小. 从图中也可以看出，增大外激励幅值，系统的幅值增大，与图 3 对应.

图 6 机械载荷与稳态响应幅值的关系Fig.6 Steady state response amplitude-mechanical loads curves

图 7 为对方程组(26)做数值积分，利用Matlab数值求解出的动相平面内相轨迹图. 取参数T0=40 ℃，η=0.1，ζ=0.3，q0=0.07 MPa. 当调谐参数改变时，稳态解的个数也随之改变. 图7(a) 中S1,S0,S2与图7(c)中调谐参数ϑ=-1 时的三个响应解对应. 其中S1,S2是稳定焦点，S0是鞍点，过S0的分割线划分出S1或S2的不同吸引盆，可能出现主共振的区域. 系统的初始状态决定了系统状态最终被吸引到哪个点，但系统状态很难被吸引到S0. 图7(b)中S3与图7(c) 中ζ=0时的响应解对应，只有一个稳定焦点S3. 因此，在工程应用中，选择合适的初始条件可以使系统处于更加安全、 高效的工作状态.

图 7 动相平面轨迹图Fig.7 Moving phase plane trajectory

4 结 论

本文针对温度场及外激励作用下压电圆形薄板的非线性主共振问题进行了研究，并用Matlab 软件进行了数值模拟. 研究结果表明：

1) 温度场中受外激励作用的压电圆形薄板的共振曲线向左偏移，呈现软刚度特性，这是由非线性项系数κ3<0引起的，在T0=40 ℃，当ω/ω0<0.86或ω/ω0>0.94时，系统出现一个响应幅值，当0.86<ω/ω0<0.94时，系统出现3个响应幅值. 因此，在系统响应中存在两次跃变及多值区间，具有明显非线性特性.

2) 对于软刚度系统，当ϑ<0时，主共振幅值随着ϑ的增大而减小，出现跳跃、 多值现象，当ϑ≥0 时，主共振幅值随着ϑ的增大而减小，跳跃、 多值现象消失.

3) 当阻尼系数、 板中心温度，板的厚度增大时，系统的响应幅值降低，发生跳跃的外激励频率与固有频率的比值增大. 板中心温度及板厚度相当于阻尼的作用. 随着外激励幅值的降低，系统的响应幅值及多值区间被抑制，共振区间逐渐变窄. 但非线性类型保持不变. 系统阻尼、 板中心温度、 外激励幅值、 板厚等参数对压电圆形薄板工作状态影响非常大. 适当地调节参数，可以使系统处于更优良的工作状态中.

4) 在动相平面轨迹图中，ϑ=-1时，对应幅频特性曲线的三个幅值. ϑ=0时，对应幅频特性曲线的一个幅值. 幅频特性曲线图中，上下分支是稳定解，中间虚线部分是不稳定解，因此系统的初始条件对系统稳态解的个数和稳定性有很大影响. 在工程应用中，选择合适的初始条件可以使系统处于更加安全、 高效的工作环境.