考虑超级网络广义重叠的路径选择建模

马 捷，程禹茜，李大韦，陈人杰

1)东南大学交通学院，江苏南京 210096；2)新加坡国立大学工程学院，新加坡 117575；3)吉林大学外国语学院，吉林长春130022；4)东南大学城市智能交通江苏省重点实验室，江苏南京 210096；5)东南大学现代城市交通技术江苏高校协同创新中心，江苏南京 210096；6)厦门市城市规划设计研究院，福建厦门 361004

交通分配的核心之一是路径选择，其在交通运输网络的应用中具有重要意义．在估计出行者对路径特性的感知、基于假设场景预测出行行为、预测交通网络的交通环境以及研究出行者对信息的反应和接受行为等方面，交通分配和路径选择建模显得至关重要[1]．

考虑路径选择的交通分配模型具有重要理论意义和应用价值． PRATO[1]总结了交通领域交通分配建模的相关研究．BEN-AKIVA等[2]提出的随机效用理论(random utility theory, RUT)是路径选择研究中应用最为广泛的理论．在这个框架下，多项logit(multinomial logit, MNL)模型是交通分配问题中应用最简单的模型[3]，被广泛应用于基于随机用户均衡(stochastic user equilibrium, SUE)的模型中．然而，MNL模型假设误差项独立同分布(identically independently distributed, i.i.d.)，在路径选择中，这样的假设会由于路径选择项的重叠效应造成有偏估计的问题．

为说明效用随机部分的相关性，前期研究提出广义极值(generalized extreme value, GEV)模型，一些计算机和行为的问题在应用GEV模型时有所研究[1]．此外，多项式probit模型和logit kernel模型通过因子分析形式也能解决路径重叠问题[4]．

在交通分配部分，在基于logit的随机用户均衡模型中，路径重叠问题的影响已被重视[5]．然而，之前几乎所有关于路径重叠问题的研究，仅考虑单一的交通方式网络，未考虑出行方式之间的重叠．最近的研究将超级网络呈现在统一网络上[6-8]，但鲜有讨论路径选择肢的相关性．

本研究在超级网络下，提出广义路径选择问题的整体结构，利用多层次混合logit模型处理广义重叠问题[9]．基于路径选择模型，提出超级网络下交通分配问题的数学表达．根据算例研究，分析广义重叠对路径选择预测和交通流均衡的影响．结果表明，物理路段和运输方式的随机项都会对路径选择概率产生重要影响，本研究提出的方法能够有效解决广义重叠问题．

1 广义路径选择和重叠问题

利用简化案例说明路径选择和路径重叠问题，图1为示例网络．出行者往返于O点和D点，其间具有路段、公共汽车路线及地铁路线3种交通设施．实际可供出行者使用的交通方式却多于3种，如私人小汽车、出租车、按需服务(Uber和滴滴等)、公共汽车和地铁线．出行者在1次出行中可以使用多种交通方式．

图1 示例网络Fig.1 An illustrative network

图1共展示4条不同路径．路径为O—B—D全部由物理路段(实线)组成，表示这是一次私人小汽车的出行；路径为O—A—B—D则由物理路段和公交线路(虚线)组成，表示这是一次小汽车换乘公交的出行；路径O—A—C—D表示一次私人小汽车出行；路径O—A—D则表示一次私人小汽车换乘地铁的出行．此外，这4条路径既有路径重叠又有出行方式重叠，例如后3条路径都在路段O—A处发生路径重叠，而前两条路径在路段B—D处发生出行方式的重叠．

在基于随机效用理论的路径选择建模中，路径选择肢的效用方程分为系统确定项和不可观测的随机项两部分．基本的MNL模型假设选择肢的随机项之间相互独立，而在路径选择中这个假设不能满足．有重叠的路径选择肢的随机效用具有相关性，因为它们都有重叠路段部分的不可观测因素，即重叠问题．文献[4]将重叠问题放在单一出行方式的道路网中，主要讨论物理路段的重叠问题．

本研究探索超级网络中的广义路径选择建模．出行者可以使用多种交通方式完成1次出行．例如，有2个广义路径(generalized routes, GRs)可以选择：GR1为路线O—B乘出租车，路线B—D乘公共汽车；GR2为路线O—A—B—D乘出租车．

对于这两条广义路径，导致其随机效用之间具有相关性的原因为：① 共享同一出行方式，即出行方式的重叠，O—B和O—A—B—D的出行方式都是出租车；② 共享同一条物理路段，即出行路径的重叠，乘坐公交的B—D和乘坐出租车的B—D均使用相同路段BD． 文献[6-8]中已有的路径选择模型并未同时考虑这两个因素．以下将提出一个弹性方法，以考虑广义重叠问题．

2 方 法

2.1 路径选择模型的超级网络表述

在建立模型之前，首先提出用以表述所研究交通网络的超级网络结构，如图2．在超级网络SN={N0,N1,…,Nm,…,NM}中，Nm={Pm,Am}表示每种出行方式所代表的网络．其中，N0是由图2中的转移路段和其他网络中的结点组成的转移网络；N1表示活动网络，由代表活动位置的结点组成的网络，如出行的起讫点；Pm={pm,n}表示网络Nm中的路段集合，n为物理结点的标签，即图1中的A—D点；Am={am,l}表示Nm网络中的路段集合，l表示物理路段的标签．因此，在超级网络中每条路段am,l除广义费用以外，还有出行方式和物理路段两项属性．

图2 超级网络结构Fig.2 The structure of super-network

2.2 多层次混合logit模型

在原始MNL模型中，路径i的效用函数为

Ui=αTYi+εi

(1)

其中，Ui为路径i的随机效用；Yi为观测到的路径特性向量；α为出行者对路径特性偏好的待测系数向量；εi为独立同分布假设下，具有标准参数的I型极值分布的随机项．

由于需要满足i.i.d.假设，本研究提出如下多层次混合logit模型，以解决广义重叠问题．

首先，根据是否可按路段相加将路径特性分为两个部分，则效用函数可表示为

(2)

ρm,l=(γTm+ηTl)Xm,l

(3)

其中，γm为满足均值为0正态分布的出行方式特性；ηl表示满足均值为0正态分布的物理路段特性；γm、ηl及εi之间两两相互独立．根据这一特性，ρm,l的标准差为路段特性Xm,l的比例．因此，效用函数可扩展为

αTYi+εi

(4)

η={ηl|l=1,2,…,L}

其中，o和O分别为观测特性的序列数和总数；l和L分别为物理路段的序列数和总数；m和M分别为出行方式的序列数和总数．

由于路段数量较大，为减少参数数量，令ηl的所有路段的第o个观测特性都满足i.i.d.假设，且符合均值为0、标准差为σo(η)的Gumbel分布．

广义重叠问题是由可选路径之间的随机效用相关性衍生而来．在式(3)的MNL模型中，路径效用的随机部分仅考虑可选路径的路径特性随机项εi， 且该项是假设为i.i.d.．而在本模型中，路径效用的随机部分由两部分衍生而来，分别是独立同分布的路径特性εi及与γm和ηl相关的超级网络路段特性的总和．因此，由于共用了同样的γm和ηl， 不同路径效用之间产生相关性．

随机项γm和ηl表示超级网络中出行者未观测到的网络特性．在传统MNL模型中，偏好系数β是常数．而在本研究模型中，出行者对于超级网络的路段偏好是随机的，由常数部分β、 未观测的出行方式特性γm及未观测的物理路段特性ηl组成．由于共享了相同的随机项γm， 因此，超级网络路段同一出行方式的随机效用是相关的；由于共享了相同的随机项ηl， 因此超级网络路段同一物理路段的随机效用也是相关的．

根据效用函数特性，给定选择集和参数之后，选择广义路径i的概率Pn(i|Cn,β,α,Σm,Σl)为

Pn(i|Cn,β,α,Σm,Σl)=

E[Pn(i|Cn,β,α,γ,η)]=

f(γ|Σm)f(η|Σl)dγdη

(5)

其中，

Pn(i|Cn,β,α,γ,η)=

由于式(5)不具有一个闭合形式，因此Pn(i|Cn,β,α,Σm,Σl)可由式(6)近似得到

Pn(i|Cn,β,α,Σm,Σl)=

(6)

其中，D为随机抽样次数；γd和ηd为第d次抽样得到的γ和η值．

基于广义重叠问题的概率选择模型，在交通分配中广义均衡路径流可由以下不动点问题描述：

(7)

其中，f*为均衡状态下的路径流；f为广义路径上的乘客流；q为交通需求；P为由式(6)计算得到的路径选择概率；Cw是OD对w之间的广义路径选择集；fr,w为OD对w之间第r条广义路径的路径流；qw为OD对w之间的交通需求．

3 算例研究

本节使用若干算例说明广义重叠问题在非集计的路径选择预测问题，及集计的交通分配问题中产生的影响，算例均基于图1的多层次网络进行研究．值得注意的是，虽然这些算例都是基于简化网络进行，但所得结论对于实际尺度的网络依然有效．

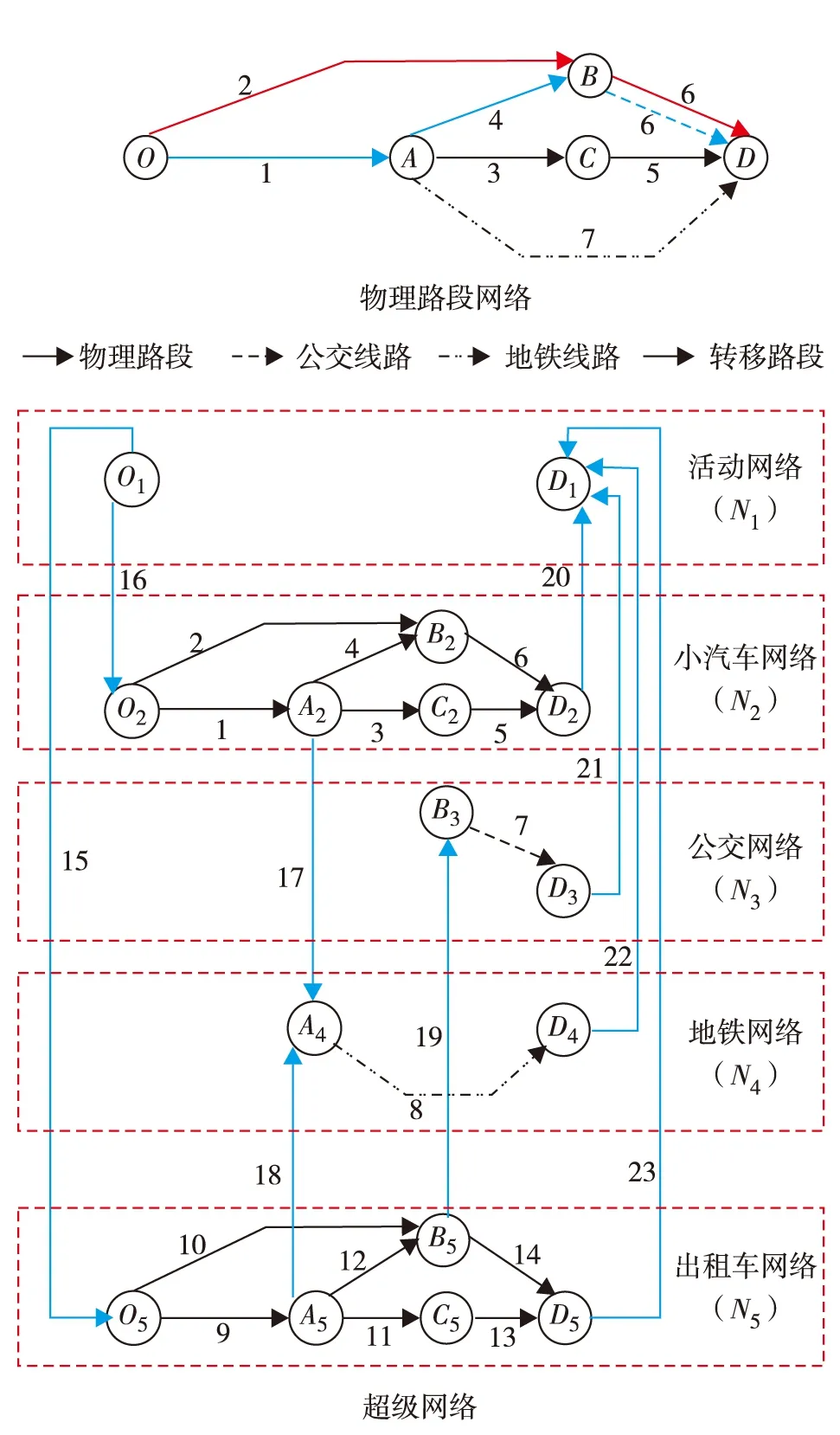
图3 示例网络的超级网络模型Fig.3 (Color online) Super-network representation of illustrative network

3.1 超级网络表述

应用2.1节所述方法，图1所示的网络可扩展为图3的超级网络．物理路段的标号和超级网络的路段标号分别在图3中的上层和下层网络路段实现．该超级网络包含6个网络层：N0为转移网络；N1为活动网络(即出行的起讫点)；N2为私人小汽车网络；N3为公交网络；N4为地铁网络；N5为出租车网络．表1为该超级网络的路段特性，其中，路段容量的单位是车/h，即veh·h-1．

表1 路段的观测特性

在交通网络中，同一种出行方式会同时存在不同类型的用户，这种现象称为多用户现象．例如，私人小汽车出行既存在传统小汽车用户又存在电动小汽车用户，文献[10]为此建立电动小汽车网络．此外，不同类型用户承担的出行费用可能也不同．如在电动小汽车网络中，用户除了承担出行时间费用外，还承担环境费用等[10]．本研究关注传统用户的常规出行方式(私人小汽车、公交、地铁及出租车)的广义重叠问题，因此，基于文献[11]对路段费用进行假设．由于本研究重点是广义重叠问题，该问题与确定型的费用无关，因此，对这些假设作出以下简化．

方式0(转移网络) 为达到简化目的，所有转移路段的费用都设为一个常数cT．

方式2(私人小汽车网络)仅考虑车内时间t2,l，

(8)

其中，Tl为出行的自由流时间；kl为路段l的通行能力；xl为路段l的总交通量，且

F3fr,wδ(r,w,3,l)E3]

(9)

其中， 当OD对w之间的第r条广义路径通过路段am,l时，δ(r,w,m,l)=1， 否则为0；fr,w为乘客流；E3为方式3中等效于小汽车的车辆数；F3为方式3的固定频率．

方式3(公交网络) 仅考虑车内时间t3,l=t2,l， 且路径特性费用为cr,w,3．

方式4(地铁网络) 仅考虑固定的车内时间t4,l和路径特性费用cr,w,4．

方式5(出租车网络) 仅考虑车内时间t5,l=t2,l和出租车费用(该费用与出租车自由流时间Tl成正比)．

3.2 模型特性

基于超级网络的表达，每种出行方式的路段出行费用um.l为

方式0(转移网络)u0,l=(β1+γ0,1+ηl,1)cT

方式2(私人小汽车网络)u2,l=(β2+γ2,2+ηl,2)t2,l

方式3(公交网络)u3,l=(β3+γ3,3+ηl,3)t3,l

方式4(地铁网络)u4,l=(β4+γ4,4+ηl,4)t4,l

方式5(出租车网络)u5,l=(β5+γ5,5+ηl,5)t5,l+(β6+γ5,6+ηl,6)Tl

在该算例中，路径特性的观测效用只列出不可加部分．10条可行广义路径(GRs)和相应的路径出行费用为

在该算例中，表1表明路段的观测特性，并设cT=2、c4,4=c8,4=2.5、c9,3=c10,3=2、F3=6及E3=2． 该算例在路径选择模型中共有19个参数，待定参数β、出行方式特性γm及物理路段特性ηl的均值及标准差缺省值请扫描论文末页右下角二维码．根据均衡理论，仅改变这些参数的值(不改变正负性)并不会改变费用函数的连续性和单调性，因此，这些参数的值可以根据需要自行改变．

3.3 路径选择预测

路径选择最直接的应用是交通分配问题，整个路网的交通流量受交通需求和路径选择机理的影响很大[12-15]．广义路径重叠问题会影响出行者的路径选择，从而影响交通分配结果．假设交通流为0，给定如下的超级网络和模型特性，则路径选择概率可通过式(6)预测．令① 所有σ2(η)的变化范围为(0, 7.2)， 所有σ2(γ)=0； ② 所有σ2(γ)的变化范围为(0, 7.2)， 所有σ2(η)=0； ③ 所有σ2(γ)和σ2(η)相等，且变化范围为(0, 3.6)， 则(σ2(γ)+σ2(η))的变化范围为(0, 7.2)；

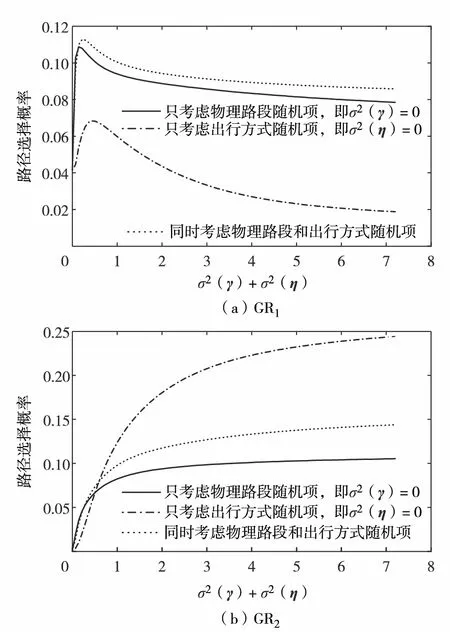
图4 物理路段和出行方式随机项对路径选择概率的影响Fig.4 The effects of mode and physical link specific random terms on route choice probabilities

模型中的其余参数均设为缺省值．则GR1和GR2的选择概率如图4(a)和4(b)．为简化表述，此处只显示路径GR1和GR2．

由结果可知，物理路段和运输方式的随机项都会对路径选择概率产生重要影响，且在相同的标准差水平下，物理路段和运输方式随机项对路径选择概率的影响不同．

在MNL模型中，当独立随机项的方差增加时，所有选择肢的选择概率会趋于相等．然而，在本模型中，当随机项方差增加时，所有路径的选择概率并没有趋于相等(而趋于0.1)，这是因为这些路径之间并不相互独立．这一点也反映了本模型能够用以处理重叠问题．

结 语

本研究探讨超级网络上的路径选择模型．在一个超级网络中，出行者有可能在一次出行中选择多种方式，例如，已有城市开展停车换乘服务．构建超级网络可将多方式交通系统呈现在一个统一的网络中，同时单一方式的交通系统也可直接应用于超级网络中．为解决广义重叠问题，本研究提出多层混合logit模型，可将超级网络下的随机用户均衡表示为一个不动点问题．通过算例说明广义重叠问题对出行路径选择的影响．分析不同物理路段及出行方式的误差项，讨论广义重叠问题下的路径选择特性．结果表明，该模型能够有效解决广义重叠问题．本研究模型算法仅在一个新的网络算例上进行验证．未来研究中，将利用偏好调查数据和智能手机数据，检验预测效果并与其他模型进行比较．

致 谢:衷心感谢东南大学程琳教授、孟强教授及李大韦教授的帮助！