基于等维灰数递补模型的路面性能预测方法

赵 静，吴旺杰，王选仓，李善强,2，房娜仁，邓瑞祥

1)长安大学公路学院，陕西西安 710064；2)广东华路交通科技有限公司，广东广州 510420

截至2018年末，中国高速公路总里程已有14万km，位列世界第一[1].路面在行车荷载以及环境等因素作用下其使用性能会不断衰减，进而影响行车舒适度及行车安全，所以，养护干预显得尤为重要.收集道路使用期内的路况数据，并据此评价道路使用性能，根据评价结果预测未来路面使用性能的衰减走向，已经成为当前道路养护工作的核心.

现有预测路面使用性能的方法主要有概率型与确定型[2].概率型是指预测路面使用性能随时间的分布特征，主要预测方法有马尔可夫法[3]、神经网络法[4-5]以及粗糙模糊集法[6]等；确定型是指根据力学模型及力学经验模型预测某项指标的具体值.预测模型的选择至关重要[7]，目前国内常采用的灰色预测模型不能有效利用新的路面使用性能检测结果，本研究建立了等维灰数递补模型用来预测沥青路面使用性能，以广云高速公路为研究对象，利用等维灰数递补GM(1, 1)模型在预测的过程中可以有效利用新的数据提高其结果的准确度，基于2011—2017年以来的路面使用性能历史数据，并结合实际的运营状况，建立了车辙指数(rutting depth index, RDI)预测模型，并根据模型预测了路面状况指数(pavement condition index, PCI)、行驶质量指数(riding quality index, RQI)和横向力指数(skidding resistance index, SRI)，为路面使用性能的预测提供了新方法.

1 静态灰色预测模型的建立

灰色预测模型GM(1, 1)是用来解决不确定性问题的新途径，其主要原理是用微分的数学模型对含有不确定、不完全信息的研究对象进行预测.建模过程中，通过研究对象数据的累加，将规律不明显的研究对象白化，减少研究对象的随机性和波动性.

1.1 静态灰色GM(1, 1)模型的构建

路面使用性能指标主要是指PCI、RQI、SRI和RDI.本研究主要以RDI的历史检测数据为基础建立预测模型，并利用该模型对其他指标进行预测.假设x(0)=(x(0)(1),x(0)(2),…,x(0)(n))为GM(1, 1)模型中的RDI历史检测数据原始序列.其中，x(0)(n)为第n年的RDI检测值.此序列不具有明显规律性，且明显波动[8].

对x(0)进行1次累加后所得到的序列为x(1)=(x(1)(1),x(1)(2),…,x(1)(n)). 累加计算方法为

x(1)(1)=x(0)(1)

(1)

(2)

对累加生成的x(1)(1)建立方程为

(3)

其中,x(1)为1次累加序列；x(1)(n)为1次累加序列中第n项；a为发展系数；b为灰色作用量.

令z(1)为x(1)的均值序列，计算方法为

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(4)

z(1)=(z(1)(1),z(1)(2),…,z(1)(n))

(5)

其中,z(1)为均值序列；z(1)(k)为均值序列中第k项.

该方程的解为

k=0,1,2,…,n

(6)

系数a和b的计算方法为

a=[a,b]T=(BTB)-1BTY

(7)

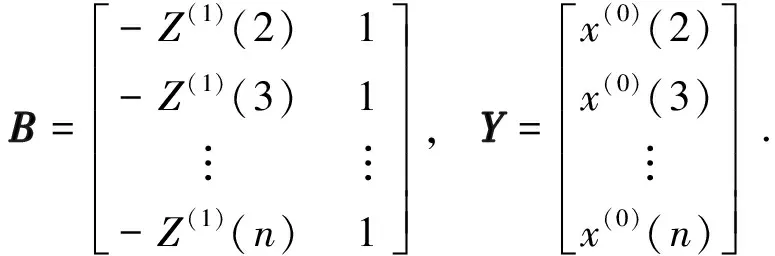
所以，GM(1, 1)预测模型为

k=0,1,2,…,n

(8)

1.2 灰色模型的精度

通过GM(1, 1)模型得到预测的结果后，还需要对模型精度进行检验，若精度符合要求便可对数据进行预测[10].模型的精度一般是通过残差e、 后验方差比C和最小误差概率P的计算来检验，计算方法如下.

1)残差检验.残差体现了预测结果与实际数据的偏离情况，其绝对值越小表示预测结果越接近实际值.

(9)

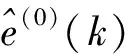
2)后验方差检验.后验方差检验包括后验方差比C值与最小误差概率P. 后验方差比C值计算方法为

(10)

最小误差概率P是根据e值的大小，考察其较小点出现的概率，其计算方法为

(11)

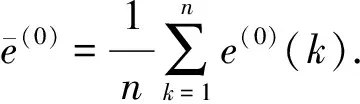
3)模型的分级.在运用模型预测之前，首先需对其进行检验，以判断该模型的准确性与精度[11].预测模型可以根据C和P值分成4个等级，具体分级见表1.若C和P值在2级以上，便认为该预测模型可以很好地对路面使用性能进行预测.最小误差概率P越大，后验差比值C越小，则模型的稳定性与精确度越高.

表1 GM(1，1)模型精度等级

2 等维灰数递补模型的建立

GM(1, 1)模型是常规的灰色模型，属于静态灰色模型.由于该模型只采用了固定数量的检测数据对未来路面使用性能进行预测，所以只能利用短期数据进行精确预测.在预测更长时间的数据时，随着时间的增加，该模型受到外界干扰因素将不断增加，精度会降低，可信度变小.因此，在常规的静态模型的基础上，建立等维灰数递补GM(1, 1)模型.此模型是一种动态模型，其本质在常规的静态GM(1, 1)模型的基础上引入已知的信息，或者灰色的信息，从而准确反映系统的变化. 实时增加新数据的同时，剔除旧数据，更能反映系统当前特征. 由传统灰色模型改进后的模型称为等维灰数递补GM(1, 1)模型[12].建模过程如下：

(12)

(13)

3 GM(1, 1)模型应用于沥青路面的使用性能预测

广云高速位于广东省粤西地区，2004年12月建成通车，全长37.331 km，双向4车道，沥青路面设计标准见表2，路面结构见表3.

本研究以广云高速公路2010年铣刨重铺的GAC-16路面作为研究样本，选取梧州方向桩号AK55+000～AK56+215段2011—2017年检测数据(表4). 以2011—2016年的RDI为原始数据，采用改进后的预测模型，以Matlab软件为建模工具，对2017年的RDI进行预测，并与当年实际值进行对比，同时对2018年的车辙指数进行预测.

表2 沥青路面设计标准

表3 广云高速公路路面结构

RDI实测数据和精度对比分别见表5和表6.其中，A为常规静态灰色模型；B为等维灰数递补第1步建模；C为等维灰数递补第2步建模；D为等维灰数递补第3步建模.不同步数下RDI预测值与实测值对比见图1，2017年不同步数下的残差见图2.

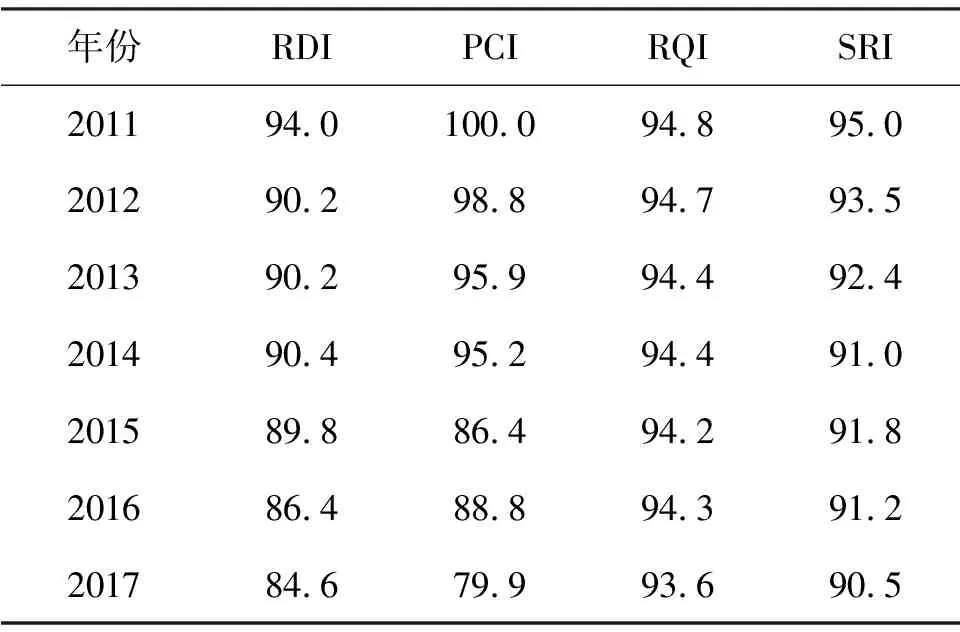
表4 广云高速2011—2017年路面RDI指数统计

表5 不同模型对RDI的预测结果对比

图1 RDI实际值与预测值对比Fig.1 (Color online) Comparison of the actual and predicted values of the rutting index

参数ABCDP1111C0.220 50.176 10.136 60.111 7等级好好好好

图2 不同步数残差变化趋势Fig.2 Variation trend of different step

由表5、表6、图1和图2可知，静态灰色模型、等维灰数递补模型所预测的RDI值与实际检测的RDI值随时间衰减趋势大致吻合.但可以明显看出，在使用等维灰数递补模型时，随着动态步数的增加，其预测值越来越接近实际值，步数增加的同时后验方差比与残差都呈现下降趋势.在第3步预测时后验方差比为0.111 7，残差为0.88，预测精度较高.根据中国《公路养护技术规范》规定：车辙状况评价为中等，车辙状况评价为良，车辙状况评价为优.所以2010—2014年期间车辙状况为优，在2015—2018年期间车辙状况为良，在此期间可进行微表处等简单的养护措施.在2019年后可采取薄层罩面处置措施对路面进行路面养护. 根据本研究预测模型，分别对PCI、RQI和SRI指标进行了预测，预测结果见图3至图5. PCI、RQI和SRI的精度对比分别见表7至表9.从图3至图5可知，在使用等维灰数递补模型对PCI、RQI以及SRI等指标进行预测时，预测结果与实际值有较高的一致性，其预测精度随着步数的增加均逐渐减小，在第3步预测时PCI后验方差比为0.065 4，残差为0.449 8；RQI后验方差比为0.201 8，残差为0.010 9；SRI后验方差比为0.113 0，残差为0.001 1.对此3项指标的预测精度均较高.说明等维灰数递补模型道路路面使用性能指标在预测中具有良好的稳定性与可靠性.

图3 PCI实际值与预测值对比Fig.3 (Color online) Contrast diagram of PCI actual value and predicted value

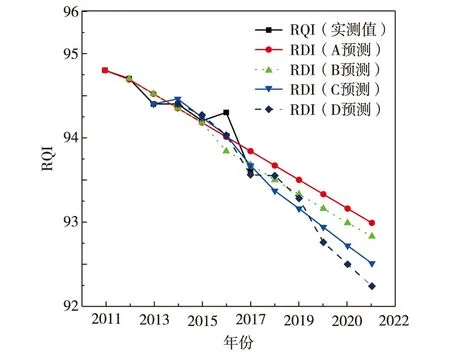
图4 RQI实际值与预测值对比Fig.4 (Color online) Contrast diagram of RQI actual value and predicted value

这是由于等维灰数递补模型利用新的预测数据，使得系统灰色区间的白色化，对各项指数进行预测后，由于在每一步中都加入新的数据信息，系统受到外界干扰越来越少，预测的精度和稳定性也在逐步提高；随着步数的增加，后验方差C也在逐渐减小.这也说明了采用等维灰数递补模型后，模型的精确度较高，步数越多其稳定性及精度越好.

图5 SRI实际值与预测值对比Fig.5 (Color online) Contrast diagram of SRI actual value and predicted value

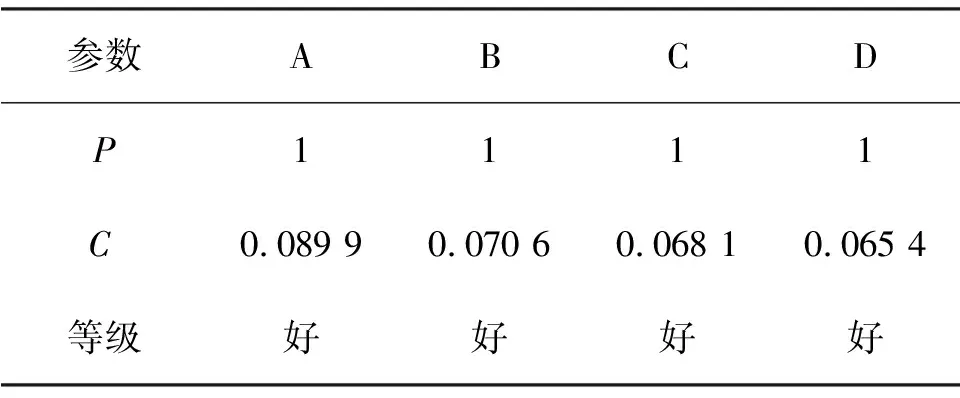
参数ABCDP1111C0.089 90.070 60.068 10.065 4等级好好好好

表8 RQI精度对比

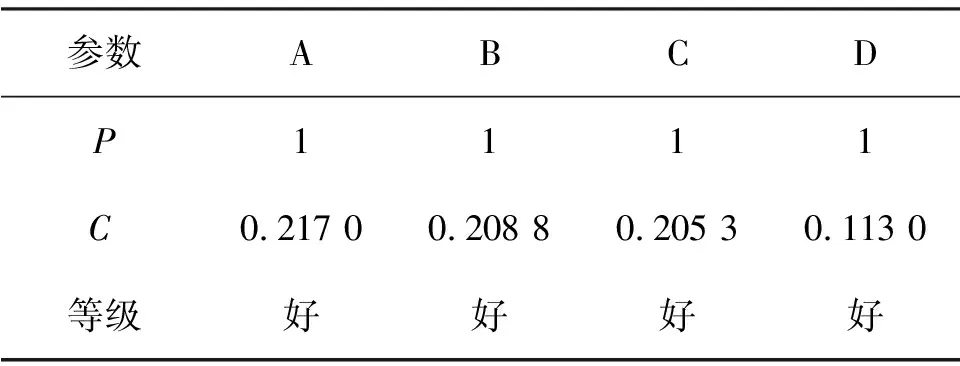
表9 SRI精度对比

4 结 论

研究了等维灰数递补预测模型在路面使用性能中的应用，挖掘了广云高速历史累计信息，建立了沥青路面使用性能预测模型.

1)对比分析了一般静态灰色模型，由于静态灰色模型对路面使用性能的预测值区间较大，精度会随着时间的延长逐渐降低，且数据序列较长时会受外界因素干扰.在此基础上提出和建立了等维灰数递补灰色预测模型.

2)利用等维灰数递补灰色预测模型对PCI、RQI、SRI和RDI进行预测.结果显示，预测值与实际值具有较高的一致性，且其精度随步数的增多逐渐提高，在第3步预测时，其最小误差概率都为1，后验方差比分别为0.111 7、0.065 4、0.201 8和0.113 0，证明了该方法能够准确地预测路面使用性能指标.

3)等维灰数递补预测模型比较简单，且准确度较高，并且能够剔除无效数据，更换新数据，能够对路面使用性能的各项指标进行精确预测，为沥青公路的养护及费用决策提供了新的预测方法.