复卷机加减速过程中纸幅张力变化的研究

李杰超

1 研究复卷机加减速过程中纸幅张力变化的意义

至今对复卷机纸幅张力变化及控制的研究通常以复卷机辊组线速度为恒定值作为前提条件，忽略了辊组由启动并加速到额定线速度，并由额定线速度减速到停止的运行过程。在实际生产中，复卷机辊组必定存在加速和减速的过程，甚至有某些启停式复卷机，由于其生产的成品纸卷直径较小，复卷机辊组几乎是在启动加速和减速停止的过程中完成每一条纸卷的复卷，其匀速运行的时间十分短暂。因此，研究复卷机辊组加减速过程中纸幅张力的变化有着重要的意义。

2 复卷机工作过程中辊组的运动规律

一般复卷机上安装有多个辊组，如送纸辊组、压光辊组、复卷辊组等。为了便于研究，对复卷机上的辊组进行简化（如图1所示）：纸幅依次从辊组1及辊组2中通过，在通过过程中忽略辊组对纸幅的挤压作用以及纸幅沿辊面可能发生的相对滑移，并且两辊组的辊面线速度相互独立、互不干扰，按预定的规律进行变化（该线速度变化可通过变频器控制多个电机对各辊组进行单独传动及速度控制实现，现已被广泛运用到各类复卷机当中）。

在复卷机启动加速到减速停机的过程中两辊组辊面线速度的变化如图2所示，辊组1及辊组2同时启动并分别以不同的加速度匀加速到额定线速度，然后保持额定线速度稳定运转，接着分别以不同的减速度匀减速到停止。

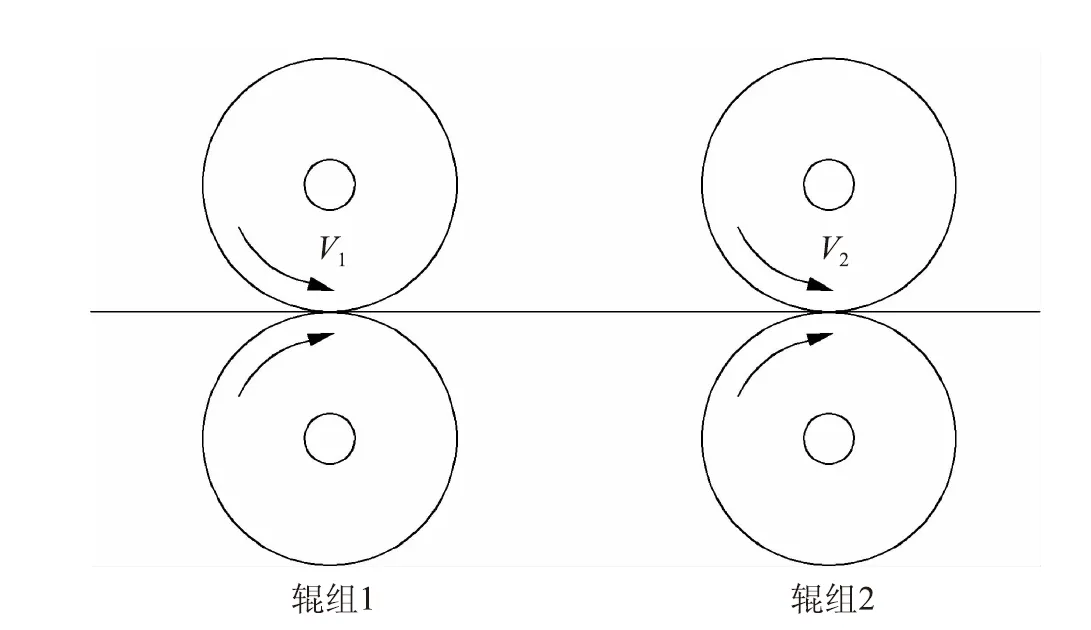
图1 复卷机中两辊组的简化形式

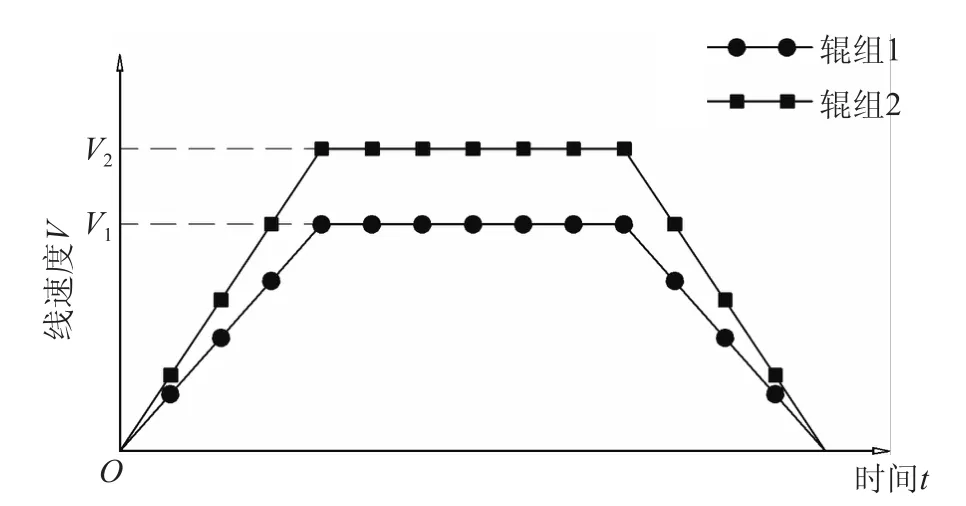
图2 复卷机工作过程中两辊组的辊面线速度变化

3 辊组间纸幅张力与纸幅伸长率的关系

在上述的运动规律中，由于辊组1和辊组2存在线速度差（V1＜V2），单位时间内辊组1往两辊组间送进的纸幅长度小于辊组2带走的纸幅长度，使辊组间的纸幅发生伸长变形。在实际生产中，为了避免纸幅定量不均、保证纸卷品质，辊组间纸幅发生的伸长变形绝大多数为可恢复的弹性变形。而纸幅为了从弹性变形恢复到原有状态，与前后辊组有着相互的拉力作用，而纸幅张力就是在该拉力作用下存在于纸幅内部截面的相互牵引力。可见，纸幅张力与纸幅的伸长变形为内力与形变的关系。假设在纸幅的弹性变形中，纸幅有固定的弹性模量且忽略其截面积的变化，则纸幅张力T与纸幅伸长率δ成正比关系，其关系式［1］为：

式中，A为纸幅的截面积，E为弹性模量。

从式（1）可知，可通过分析辊组间纸幅的伸长率δ，来探讨复卷机匀加减速过程中辊组间纸幅张力的变化。

4 两辊组匀加速过程中辊组间纸幅伸长率的变化

假设进入辊组1前纸幅的伸长率为δq、原长率（纸幅原来长度与被拉长后的长度的比值）为ξq。因为在复卷机启动前辊组1与辊组2间的纸幅没有发生伸长变形，所以此时辊组间纸幅的伸长率δ0=0，原长率ξ0=1（如图3所示）。复卷机启动后，辊组1经匀加速达到额定线速度V1，其加速度为a1，辊组2经匀加速达到额定线速度V2，其加速度为a2，加速时间均为ta，两辊组传动点之间的纸幅长度为L。

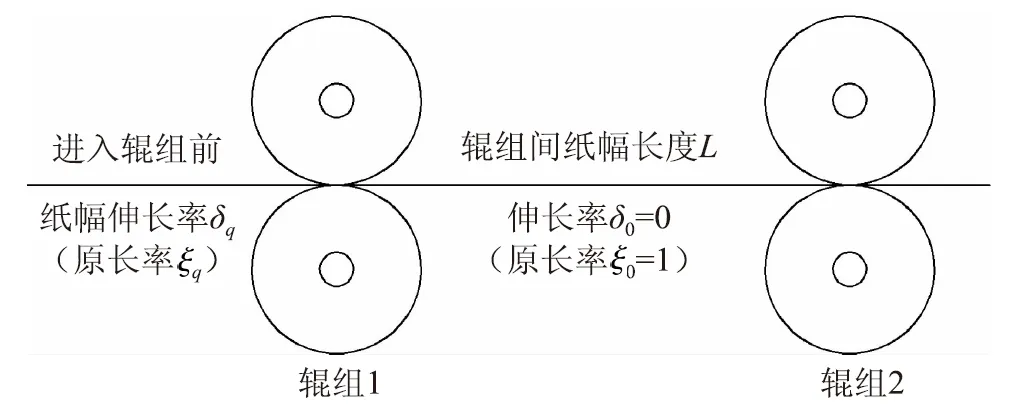
图3 启动前的两辊组及辊组间的纸幅伸长率

将两辊组启动加速期间纸幅伸长变形的过程划分为若干个细小的时间间隔，逐步分析纸幅伸长率的变化。

在第1个时间间隔Δt内，辊组1启动并加速到线速度v11=a1Δt，并往两辊组间送进长度为L11=v11Δt的纸幅，因为辊组1送进的纸幅其原长率为ξq，所以该部分纸幅的原长度应为ξq L11。而辊组2启动并加速到线速度v21=a2Δt，并从两辊组间带走长度为L21=v21Δt的纸幅，因为在启动前两辊组间的纸幅没有发生伸长变形，其原长率ξ0=1，所以该部分纸幅的原长度仍为L21。因此，在第1个时间间隔内，两辊组间纸幅的原长度O1为：

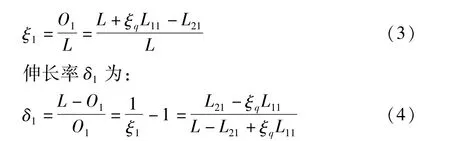
在第2个时间间隔Δt内，辊组1加速到线速度v12=a1·2Δt，并往两辊组间送进长度为L12=v12Δt的纸幅，该部分纸幅的原长度为ξq L12。而辊组2加速到线速度v22=a2·2Δt，并从两辊组间带走长度为L22=v22Δt的纸幅，因为辊组2带走的纸幅在第一个时间间隔已经被拉长，其原长率为ξ1，所以该部分纸幅的原长度应为ξ1L22。因此，在第2个时间间隔内，两辊组间纸幅的原长度O2为：

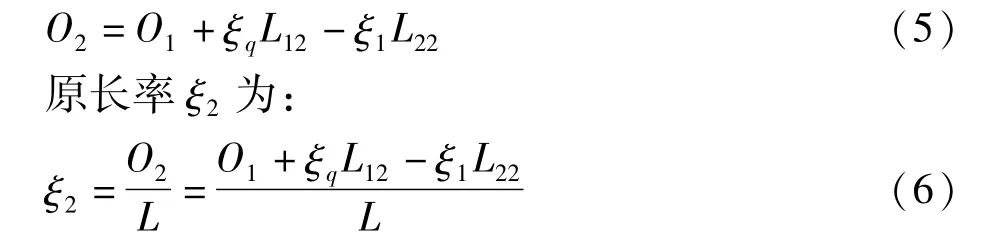
同理可推，在第3个时间间隔内两辊组间纸幅的原长度O3和原长率ξ3分别为：

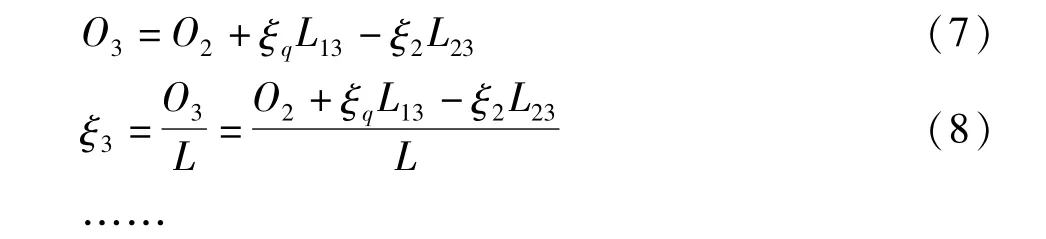
在第N个时间间隔内两辊组间纸幅的原长度ON和原长率ξN分别为：

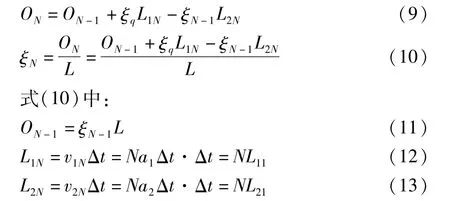
把式（11）～式（13）代入式（10），并通过变换，得：

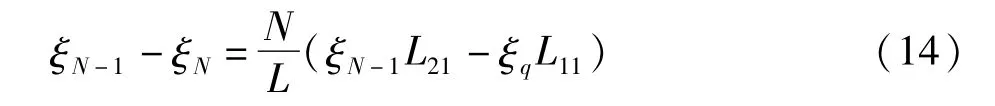
因为在两辊组匀加速过程中其线速度差逐渐增大，辊组间纸幅的伸长率δN也相应逐渐增大，原长率ξN逐渐减小，当原长率ξN减小到一定数值：

上式表明，在两辊组同时启动并分别匀加速到额定线速度V1、V2的过程中，辊组间纸幅的原长率ξN减小到一定数值后不再发生变化，为恒定值。

由上述可知，L11=v11Δt=a1（Δt）2、L21=v21Δt=a2（Δt）2，将其代入式（15），并结合式（16），得：

在文献［1］中，两辊组忽略其启动加速过程、在给定辊面线速度差V2-V1的条件下，辊组间纸幅的原长率ξ随着时间t的增长逐渐趋于一恒定值，该恒定值为：

式（18）与式（17）一致。考虑到在两辊组匀加速到额定线速度并以额定线速度持续运转的过程中，辊组间纸幅的原长率ξ是连续变化的，所以推测两辊组的线速度分别达到额定线速度V1、V2时，辊组间纸幅的原长率ξ同时达到该恒定值。

5 两辊组匀加速过程中辊组间纸幅伸长率的变化曲线

通过实例计算来探讨两辊组启动并匀加速到额定线速度的过程中辊组间纸幅原长率和伸长率的变化，从而验证上述推测。

假设辊组1的额定线速度V1为190 m/min，辊组2的额定线速度V2为200 m/min，两辊组传动点之间的纸幅长度L为0.8 m，启动加速时间ta为4 s，时间间隔Δt定为0.1 s，进入辊组1前纸幅的原长率ξq=0.98（伸长率δq=0.0204）。根据式（9）和式（10），反复递推计算各时间间隔内辊组间纸幅的原长率ξ及伸长率δ，得到实例计算的结果（见表1）。

由表1可以看出，在匀加速过程中，原长率ξ逐渐减小，伸长率δ逐渐增大，并分别趋于恒定值0.9310、0.07411。对应地使用式（17）进行计算，得：

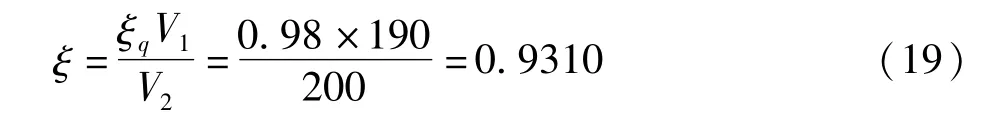
该计算结果与表1最终的递推结果一致。如果改变辊组1的额定线速度V1，例如分别取为195 m/min，199 m/min，重复以上递推过程，也将得到与计算结果一致的递推结果（该递推计算过程这里不再冗述）。

以上实例计算的结果验证了上述推测：两辊组经匀加速分别达到额定线速度V1、V2时，辊组间纸幅的原长率ξ同时达到恒定值，该恒定值为：

表1 各时间间隔内两辊组间纸幅的原长率和伸长率

此时伸长率δ也达到恒定值，为：

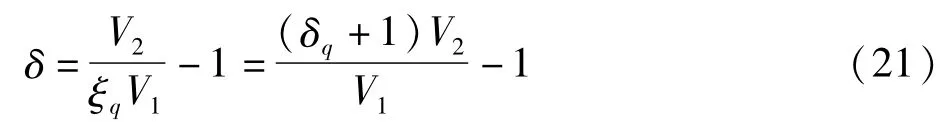
把实例计算结果绘制成图（见图4），可看出辊组间纸幅伸长率δ在这一过程中的变化。

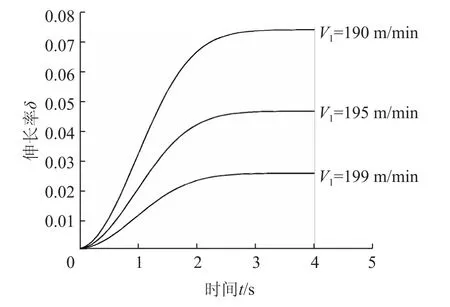
图4 纸幅伸长率δ随辊组匀加速的变化规律

6 两辊组匀减速过程中辊组间纸幅伸长率的变化

假设进入辊组1前纸幅的伸长率仍为δq、原长率仍为ξq。因为在减速前两辊组经匀加速分别达到额定线速度V1、V2，辊组间纸幅伸长率和原长率达到并保持恒定值，所以此时辊组间纸幅的伸长率δ0=（δq+1）V2/V1-1，原长率ξ0=ξq V1/V2=ξqa1/a2（如图5所示）。减速时辊组1的减速度为a3，辊组2的减速度为a4，减速时间均为td，两辊组传动点之间的纸幅长度为L。

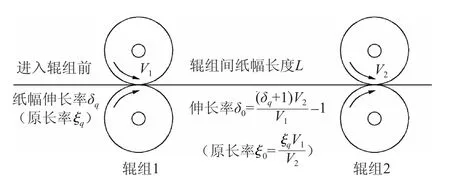
图5 减速前的两辊组及辊组间的纸幅伸长率

将两辊组匀减速到停止期间纸幅伸长变形的过程划分为若干个细小的时间间隔，逐步分析纸幅伸长率的变化。

在第1个时间间隔Δt内，辊组1减速到线速度v11=V1-a3Δt，并往两辊组间送进长度为L11=v11Δt的纸幅，因为辊组1送进的纸幅其原长率为ξq，所以该部分纸幅的原长度应为ξq L11。辊组2减速到线速度v21=V2-a4Δt，并从两辊组间带走长度为L21=v21Δt的纸幅，因为在减速前辊组间纸幅的原长率为ξ0，所以带走的该部分纸幅其原长度为ξ0L21。因此，在第1个时间间隔内，两辊组间纸幅的原长度O1为：

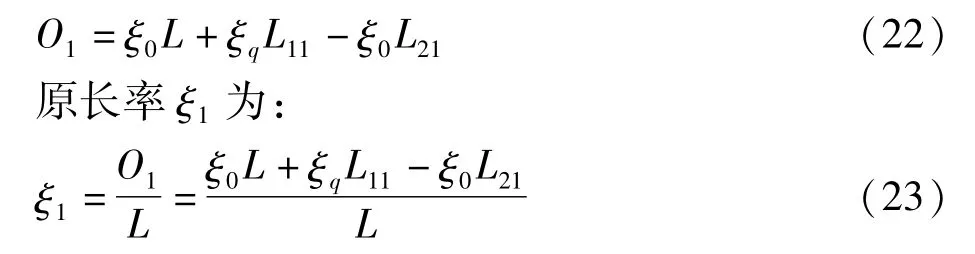
因为L11=v11Δt=（V1-a3Δt）Δt、L21=v21Δt=（V2-a4Δt）Δt，将其代入式（23），得：

由上述可知：

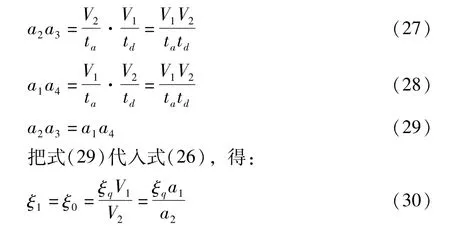
在第2个时间间隔Δt内，辊组1减速到线速度v12=V1-a3·2Δt，并往两辊组间送进长度为L12=v12Δt的纸幅，该部分纸幅的原长度为ξq L12。辊组2减速到线速度v22=V2-a4·2Δt，并从辊组间带走长度为L22=v22Δt的纸幅，因为辊组2带走的纸幅经第一个时间间隔其原长率变化为ξ1，所以该部分纸幅的原长度应为ξ1L22。因此，在第2个时间间隔内，两辊组间纸幅的原长度O2为：

同理可推，在第3个时间间隔内两辊组间纸幅的原长度O3和原长率ξ3分别为

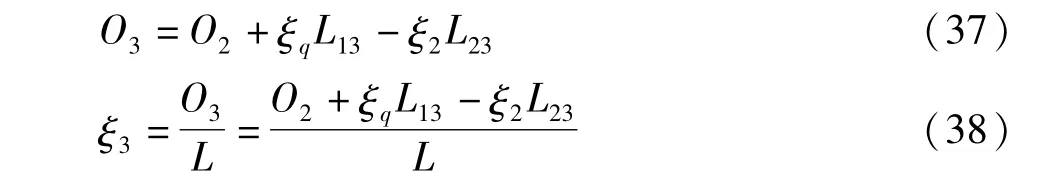
同理在第1、2个时间间隔的推导计算，对式（38）进行展开，得：

在第N个时间间隔内，两辊组间纸幅的原长度ON和原长率ξN分别为：

上式表明，两辊组匀减速到停止的过程中辊组间纸幅的原长率为恒定值，该恒定值与之前两辊组经匀加速分别达到额定线速度V1、V2时的原长率恒定值一致。

7 两辊组由停止重新匀加速到额定线速度过程中辊组间纸幅伸长率的变化

假设进入辊组1前纸幅的伸长率仍为δq，原长率仍为ξq。而两辊组间纸幅的原长率经匀减速到停止的过程后仍保持恒定值ξ0=ξq V1/V2（如图6所示）。重新启动后辊组1经匀加速达到额定线速度V1，其加速度仍为a1，辊组2经匀加速达到额定线速度V2，其加速度仍为a2，加速时间均仍为ta。

将两辊组重新启动加速期间纸幅伸长变形的过程划分为若干个细小的时间间隔，逐步分析纸幅伸长率的变化。

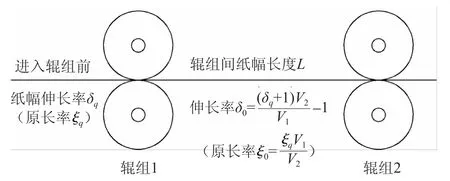
图6 重新启动前的两辊组及辊组间的纸幅伸长率

在第1个时间间隔Δt内，辊组1重新启动并加速到线速度v11=a1Δt，并往两辊组间送进长度为L11=v11Δt的纸幅，该部分纸幅的原长度为ξq L11。辊组2重新启动并加速到线速度v21=a2Δt，并从两辊组间带走长度为L21=v21Δt的纸幅，因为重新启动前辊组间纸幅的原长率保持恒定值ξ0，所以该部分纸幅的原长度为ξ0L21。因此，在第1个时间间隔内，两辊组间纸幅的原长度O1为：

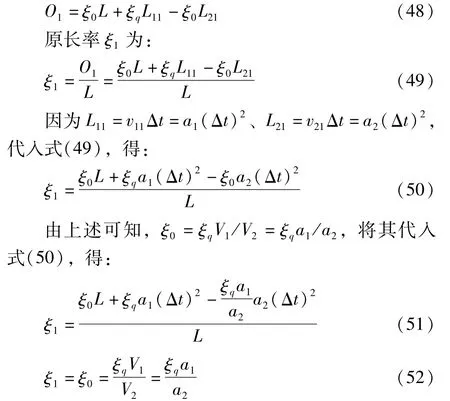
在第2个时间间隔Δt内，辊组1加速到线速度v12=a1·2Δt，并往两辊组间送进长度为L12=v12Δt的纸幅，该部分纸幅的原长度为ξq L12。而辊组2加速到线速度v22=a2·2Δt，并从两辊组间带走长度为L22=v22Δt的纸幅，因为此时辊组2带走的纸幅其原长率为ξ1，所以该部分纸幅的原长度为ξ1L22。因此，在第2个时间间隔内，两辊组间纸幅的原长度O2为：

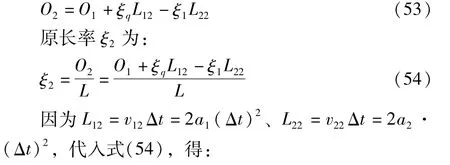
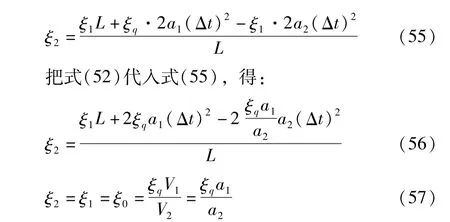
在第3个时间间隔内，两辊组间纸幅的原长度O3和原长率ξ3分别为：

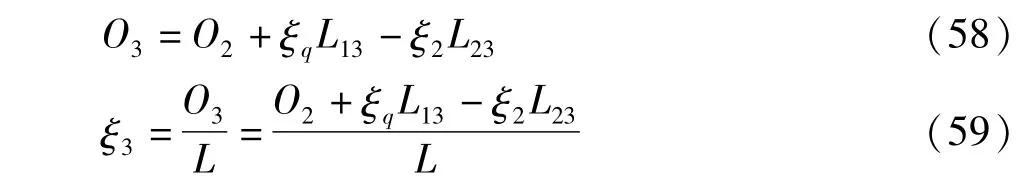
同理在第1、2个时间间隔的推导计算，对式（59）进行展开，得：

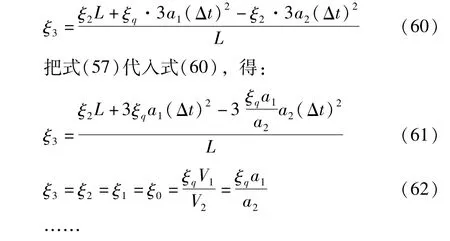
在第N个时间间隔内，两辊组间纸幅的原长度ON和原长率ξN分别为：

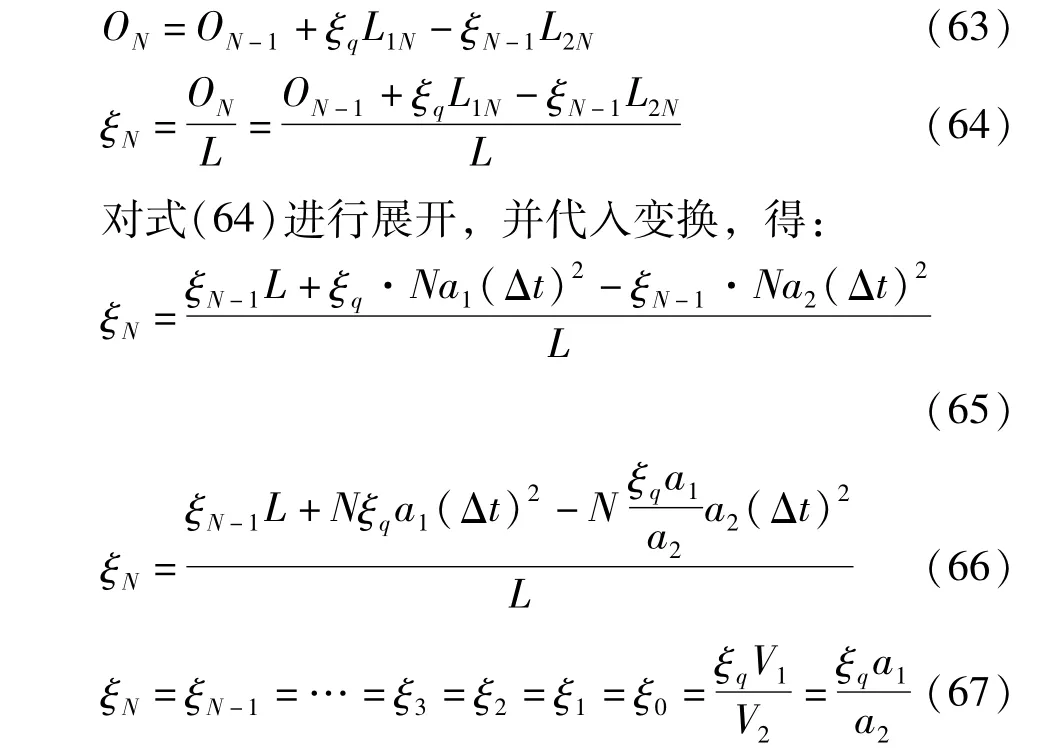
上式表明，在两辊组重新启动并分别匀加速到额定线速度V1、V2的过程中，辊组间纸幅的原长率仍保持与重新启动前一致的恒定值。

8 两辊组加减速过程中纸幅伸长率的变化以及伸长率保持恒定值的条件

综上所述，辊组1和辊组2第一次启动并分别以加速度a1、a2进行匀加速，在加速过程中辊组间纸幅的原长率ξ逐渐减小，伸长率δ逐渐增大，并且在两辊组分别达到额定线速度V1、V2的同时其纸幅原长率ξ达到恒定值ξq V1/V2，对应伸长率δ达到恒定值（δq+1）V2/V1-1。然后两辊组以额定线速度V1、V2持续运转一段时间后分别以减速度a3、a4匀减速到停止，停止结束后，两辊组又重新启动并分别以相同的加速度a1、a2匀加速到额定线速度V1、V2……在这几个工作过程以及此后重复的减速停止、启动加速过程中，辊组间纸幅的伸长率δ始终保持该恒定值（如图7所示）。

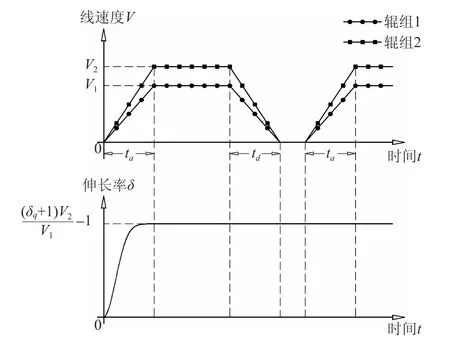
图7 复卷机加减速过程中两辊组间纸幅伸长率的变化

在纸幅的弹性变形中，纸幅张力与纸幅伸长率成正比关系，因此纸幅张力也符合以上规律，图7同样反映了复卷机加减速过程中纸幅张力的变化。

设辊组1、辊组2匀加速时间分别为t1、t2，匀减速时间分别为t3、t4，由上述的推导过程可知，在辊组1、辊组2匀减速过程中要保持辊组间纸幅的伸长率恒定，必须满足a2a3=a1a4，即：

通过设定t1=t2=ta，t3=t4=td可以使上式成立，也就是说，通过设定辊组1、辊组2的匀加速时间及匀减速时间分别相等，可使复卷机在第一次启动加速后的连续加减速工作过程中辊组间的纸幅伸长率（纸幅张力）保持恒定。

9 结 论

复卷机在第一次启动并匀加速到额定线速度时，辊组间的纸幅张力达到恒定值，在随后重复的匀减速停止及重新启动加速的工作过程中纸幅张力仍保持该恒定值。并且，可通过设定复卷机各辊组匀加速和匀减速的时间分别相等来实现这一运行规律。上述的规律和实现条件，对实际生产有重要的指导意义。

（1）该规律解释了启停式复卷机重复启动加速和减速停机仍能生产出松紧均匀的纸卷的原因：复卷过程中，辊组间纸幅张力保持恒定，进入复卷辊组的纸幅其松紧程度也保持稳定。

（2）以各辊组加减速时间分别相等为准则，对复卷机上各辊组进行速度控制，能保证启停式复卷机生产的成品纸卷松紧程度均匀一致。而对不停机的复卷生产线而言，在有需要进行停机检修时，保持辊组间纸幅状态不变，以该准则重新启动开机，能保证生产的纸卷品质不变的同时，减少调试时间，降低因停机产生的次品率。

（3）复卷机在每次更换原纸后，可通过适当减少第一次启动加速时间，降低复卷机第一次开机时产生的次品率。而对高速复卷机，适当加大减速时间，减缓减速时间的速度变化，可减轻复卷机零部件的磨损及电机发热现象。特别是车速1000 m/min以上的高速分切复卷机，减速时间的加长不会对纸卷的复卷品质产生影响，但有利于保证分切效果。