基于异步卷积分解与分流结构的单阶段检测器
2019-11-21赵蓬辉孟春宁常胜江
赵蓬辉,孟春宁,常胜江
(1.南开大学 电子信息与光学工程学院 现代光学研究所,天津300350;2.中国人民武装警察部队海警学院 电子技术系,宁波315801)
目标检测作为计算机视觉领域的关键技术,一直是具有挑战性的研究热点。Viola和Jones[1]于21世纪初提出了Viola-Jones算法首次在计算资源有限的情况下实现了实时的人脸检测。2005年,Dalal与Triggs[2]提出的HOG(Histogram of Oriented Gradient)行人检测器拓展了Viola-Jones算法的检测领域。Felzenszwalb等[3]提出的可变形部件模型(Deformable Part based Model,DPM)及其后续优化算法连续3年获得目标类别视觉挑战赛(The PASCAL Visual Object Classes Challenge)[4]的冠军,代表了当时基于手工设计特征的检测器的最高水平。然而,基于手工设计特征的目标检测器在目标区域选择上策略针对性差,窗口计算冗余量大,尤其针对环境多样性变化和遮挡问题没有很好的鲁棒性[5]。因此,早期的目标检测算法难以达到实用的要求,陷入发展停滞期。
得益于卷积神经网络的迅速发展,Girshick等于2014年提出了区域卷积神经网络结构(Regions with Convolutional Neural Networks features,R-CNN)[6],标志着目标检测摆脱了缓慢发展的困境,进入了新的发展阶段。此后涌现出的基于深度学习的目标检测算法大致可分为2类:两阶段分类回归系列与单阶段回归系列。
R-CNN主要计算流程由2部分组成,分别是类别分类和位置回归。此后,在R-CNN基础上提出的SPP-Net[7]、Fast R-CNN[8]、Faster R-CNN[9]、FPN(Feature Pyramid Networks)[10]等算法均将检测任务分成分类问题和位置回归2类问题。因此,这类算法统称为两阶段分类回归系列。随着目标检测数据集的逐渐丰富和网络训练技巧的不断优化,该系列检测算法的平均检测精度得到迅速提升。两阶段分类回归系列算法虽然能取得70%以上的平均精度均值,但其网络结构过于复杂,不仅导致前期的网络训练时间较长,也致使网络参数量较大,难以保证实时性。为获得较高的检测帧率,两阶段分类回归系列算法需要苛刻的GPU硬件配置条件,且不利于将算法移植到移动终端。提高检测精度的同时,保证检测速度日益成为工业界的实际需求。为兼顾精度与速度,单阶段回归算法应运而生。
Redmon等[11]于2015年提出的端到端一体化网络YOLO v1在VOC 07[4](Pascal VOC 2007)上取得66.4%的平均精度均值,虽然平均检测精度低于大部分两阶段分类回归算法,但检测处理速度最高可达155帧/s。此后,为提高检测精度,陆续出现YOLO9000[12]、SSD[13]、YOLOv3[14]等单阶段回归算法。这类算法将分类问题与位置回归问题统一成一个回归计算问题,与R-CNN等算法形成鲜明对比。为进一步提高平均精度均值,Liu等在SSD的基础上先后提出DSSD[15]、DSOD[16]等优化的SSD类算法。在检测流程中,SSD类算法采用锚箱[8]在多层特征图上以不同比例与尺寸的建议框进行回归计算,一次性检测物体的类别与位置。SSD类算法相对两阶段分类回归算法计算简单且参数量较少,能够在一定程度上兼顾检测精度与速度。
SSD中的多层次回归计算思想优于单一特征图上的目标检测,利于消除YOLO v1中存在的近邻目标检测“竞争”现象[11],DSSD等算法继承了SSD多层回归计算的特点,通过改进高层框架结构以提升平均精度均值。然而,SSD多层回归计算在结构上存在回归特征图(检测所基于的多层特征图层)层与层之间相对独立的情况。虽然通过高层结构改造可在一定程度上提升平均精度,但改造后的复杂结构又影响了检测速度,难以保证实时性[14,16]。
为解决SSD系列算法存在的层间回归计算相对独立的问题,保证目标检测实时性的同时,进一步提高检测精度,本文基于SSD构造了一种底层结构为卷积神经网络[17]的基于异步卷积分解与分流结构的单阶段检测器(Single Shot mutibox Detection based on Asynchronous convolution Factorization and shunt structure,FA-SSD)。在底层网络结构中,为避免网络结构过于复杂,以单链无分支的卷积神经网络结构为基础。在高层网络结构中,采用异步卷积分解的两层卷积层与池化层相结合的降维方式,保证空间相关信息的同时,提高特征的多样性。此外,FA-SSD借鉴残差神经网络[18]的交融结构,提出一种分流(shunt)结构交错连接多层回归特征图,增强多层回归计算之间的统一性与协调性。
FA-SSD网络的创新点可归纳如下:
1)借鉴Inception模型[19]中的卷积分解思想,增加了不同方向不同步长的异步卷积策略,提出一种异步卷积分解算法。采用异步卷积分解算法构造的两层卷积层,与SSD采用一层卷积对特征图降维相比,可在不增加计算量的情况下,提高提取特征的非线性表达能力。
2)基于异步卷积分解算法构造了一种shunt结构,从原有高层网络结构(主流结构)中分出包含两层采用异步卷积分解的卷积层组成的shunt结构,同时与主流结构实现特征交融,解决了各层回归计算相对独立的问题,增强了多层回归计算之间的统一性与协调性。在shunt结构中采用异步卷积分解算法构造的卷积层可在降低特征图维度的同时,增加特征图之间的交融过程,改善空间相关信息缺失的问题。
3)优化了高层网络结构中的主流结构。首先使用池化层代替原有结构中的步长为2的卷积层,在主流结构和shunt结构中同时使用池化和卷积两种降维方式,提升特征的多样性;然后在每次交融的特征图后增加一层步长为1大小为1×1的卷积层以提升回归特征图之间的卷积深度,扩大各层回归特征图间的特征差异性。
1 SSD网络结构
SSD算法的计算流程如图1所示,其中图1(a)和(b)为底层特征提取阶段,图1(b)和(c)为非极大值抑制(NMS)筛选多个检测结果的阶段,图1(b)表示多层回归特征图把分类任务与位置回归任务统一为回归问题,在高层神经网络中的多层次特征图上分别应用不同尺寸的锚箱生成特定长宽比例的建议框,并在建议框上一次性回归物体类别与位置信息,生成的建议框长宽比有“1、2、3、1/2、1/3”等。
底层结构为VGG结构的SSD网络框架如图2所示,高层结构中的多层回归特征图分别为block4、fc7、block8、block9、block10、block11。其中上述名称分别表示神经网络中每个卷积命名区域中最后的特征图层。黑色圆表示卷积(conv),采用大小为“3×3”,步长为(1,1)的两层卷积核,即2kernal3×3_s1。红色三角形表示池化(pool),采用大小为“2×2”,步长为(2,2)的一层最大池化,即 pool2×2_s2。上 述 6 层 特 征 图 层共生成8732个特定比例与尺寸的建议框,每个框架检测出的结果经过非极大值抑制筛选,得出最终检测的位置和类别。
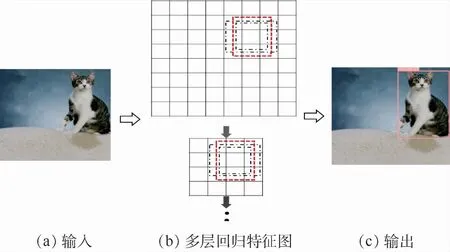
图1 SSD算法计算流程Fig.1 Computation procedure of SSD algorithm
SSD计算过程可表示底层与高层两部分。
底层神经网络计算过程可表示为

高层神经网络计算过程可表示为

式中:fp表示卷积神经网络中的池化计算(下标p表示相应特征图层);f表示卷积运算;fc7和block4,8,9,10,11表 示 回 归 特 征 图;block″1,2,3,4表 示 底层网络中每个卷积区域的最后特征图层;block′1,2,3,4表 示 卷 积 区 域 其 他 特 征 图 和 池 化 后 的特征图;Xi表示相应的特征图层;R表示回归运算;D表示分类回归与位置定位回归;∪表示范畴中的并集和特征图在通道维度上的并列交融。
SSD可通过各种复杂交叉的底层网络改善处理过程中容易丢失空间相关信息的问题以提高特征的多样性。然而,复杂的高层模型可以提高精度却难以保证实时的处理速度。由图2可见,SSD高层网络结构的回归特征图中层与层之间相对独立,致使多层回归计算难于统一,例如图2中block8与block10之间仅用单链的四层卷积层间接地通过block9进行联系,各自通过回归计算出类别与位置,无法直接建立两层之间的有效联系,不利于目标检测在网络中的协调统一。为此,本文提出FA-SSD网络,摒弃复杂的底层与高层网络结构的改进方法,仅通过优化主流结构和增加一种轻量级的shunt结构增强高层网络多层回归特征图之间的协调性与统一性。
2 FA-SSD网络结构
FA-SSD的底层网络基于VGG,高层网络为多层次的回归计算结构,如图3所示,其中红色虚线框为高层主流结构,黑色圆、红色三角形和红色菱形分别表示卷积操作(conv)、池化操作(pool)和回归特征图层之间的网络结构(nn),蓝色菱形和对立三角表示shunt结构和特征图层通道方向上的交融操作。图中特征图层的命名方式与图2相同,高层网络的回归特征图分别为block4、fc7、block8、block9、block10、block11。高 层 结 构 用 两种方式对特征图进行降维,分别是shunt结构中的异步卷积分解算法和高层主流结构中的最大池化。FA-SSD 中共有4个 shunt结构,分别是shunt0、shunt1、shunt2和shunt3,用2种连接方式增加回归特征图层之间的联系。4个shunt结构的整体连接方式如图3所示。最后在6个回归特征图上计算出类别与位置,通过NMS进行一定阈值的筛选,得出置信度最高的目标。
搭建的网络结构包含以下3部分内容。
1)异步卷积分解算法

图4 异步卷积分解算法Fig.4 Asynchronous convolution factorization algorithm
SSD的高层结构完全应用卷积层搭建,应用步长为2的一层卷积层对特征图进行降维。为提高非线性表达能力,在使用卷积进行降维的同时,提出一种异步卷积分解算法。该算法借鉴Inception模型中的卷积分解思想,采取不同方向上不同步长的异步卷积策略组合两层异步卷积分解的卷积层,图4展示了异步卷积分解算法中的一层的操作过程,其中kernel3×1s(2,1)表示大小为“3×1”的卷积核,在B方向上大小与步长分别为3和2,在A方向上的大小和步长分别为1和1。输入特征图在经过一层异步卷积分解的卷积计算后,仅在B方向实现降维。再次经过卷积核kernal1×3s(1,2)的卷积处理后,特征图在A与B方向分别降低了维度,类似pool2×2s2对特征图进行处理的效果。与SSD高层网络中的一层kernal3×3s(2,2)卷积结构相比,kernal3×1s(2,1)与kernal1×3s(1,2)的结合在未增加计算量的同时,提高了网络的非线性表达能力。与pool2×2s2的最大池化层相比,两层异步卷积分解的卷积计算既在卷积核大小为“3”方向上保证了像素之间的重叠,即在步长为“2”方向上保证了感受野之间的重叠,保留了足够的空间相关信息。
2)shunt结构
shunt中的网络结构即为异步卷积分解算法,shunt连接方式如图5所示,借鉴残差网络模型中的分支交融结构,对主流结构采用2种方式进行连接。block4与fc7之间存在每层含有512个神经元的三层卷积网络和一层包含1 024个神经元的fc6,网络层数和神经元个数大于其他回归特征图层之间的网络。为节省计算量、提高回归特征图间的联系,shunt0起始于回归特征图层block4,直接与回归特征图层block fc7在通道维度进行并联交融(后续交融或连接均为通道维度的concat交融),与其他shunt结构无交错跨越的联系。而shunt1与shunt2之间以及shunt2与shunt3之间存在交错连接,例如shunt1的交融端位于shunt2的分流(与主流相同的征信息)之后,shunt2则 可 跨 越 block9 直 接 连 接 block8 与block10。如果shunt2起始端位于shunt1交融位置之后,则会因为特征交融导致特征图通道的倍增,而增加计算量。在通道维度上进行并联交融之后,特征图层经过批归一化[20]处理及回归计算得出类别与位置信息。通过上述2种shunt连接方式增强高层网络中多层次的回归计算之间的联系,即增强协调性和统一性。
3)高层网络结构的优化及计算过程
图6展示了优化后的高层网络结构中的局部结构,其他局部结构与此类似。实验搭建了多种网络结构并进行了训练及测试,对比实验结果证明图6所示的结构取得了最好的测试效果。该结构主要由池化层pool2×2s(2,2)和shunt结构组成,池化层和shunt结构均可实现特征图的维度降低。其中pool2×2s(2,2)表示大小为“2×2”,2个方向步长为“2”的池化,kernel3×3s(1,1)表示大小为“3×3”,2个方向步长均为1的卷积核,kernal1×1s(1,1)表示大小为“1×1”,2个方向步长均为1的卷积核。
高层网络结构的优化后,6层回归计算过程可分为3个部分,即
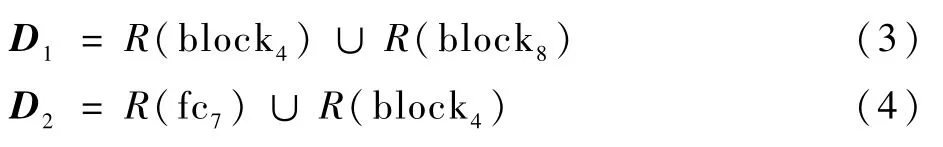

图6 高层网络局部结构Fig.6 Local structure of high-level network
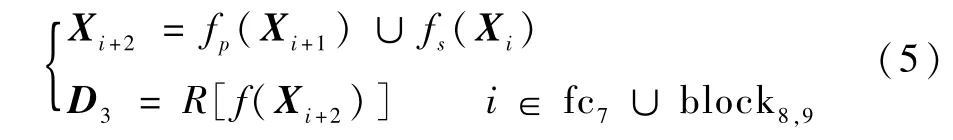
式中:fp与fs分别表示最大池化和异步卷积分解2种降维方式。
多层次的检测结果D为D1、D2和D3的并集,即
D =D1∪D2∪D3
3 实验与分析
实验所用训练数据集为VOC2007trainval与VOC2012trainval[4],检测数据集为VOC2007test[4]。实验软件配置为Window10、TensorFlow1.7.0、TensorFlow Layers API、CUDA9.0,硬 件 配 置 为NVIDIA GeForce GTX 1080Ti(一块)、Intel(R)Xeon(R)CPU E5-2609v4@ 1.70 GHz×16。实验检测的基准是算法的百分制(%)平均精度均值m_AP和检测速度v。
FA-SSD中参与训练和检测的图像大小为300像素×300像素,因此下文称FA-SSD300。回归特征图的大小分别是“38×38”、“19×19”、“10×10”、“5×5”、“3×3”和“1×1”,在上述6种回归特征图采用锚箱分别生成建议框,具体建议框参数设置和分类定位阈值设定与SSD算法相应设置相同,参与对比分析的SSD300检测结果如可见对比实验部分内容。
采用批次为16,共训练150 000步。学习率初始设置为0.01,采用分阶段控制方式间接调整目标函数优化器。衰减步长边界设置为:“20000、900 000、130 000”,学习率衰减设置为:“1、0.1、0.005、0.001”。学习率终止边界设为0.000 01,直至收敛。
为增加所用训练样本的价值,在图像预处理阶段对样本进行随机地裁剪,颜色扰动、翻转等数据增广方式。颜色扰动过程包括图片颜色的“亮度、对比度、饱和度、色相”4种调整操作,并且随机改变这4种图像颜色操作的前后顺序,最后统一压缩为“300像素×300像素”的图像进行网络训练。增广产生的数据实例如图7所示。
实验对FA-SSD的训练网络初试参数设定采用VGG参数迁移和参数初始化2种方法。其中,迁移VGG的参数是经过ImageNet[21]数据训练后获得的权重。训练过程中的损失变化如图8所示,其中loss1与loss2分别是初始化参数和迁移VGG参数下的损失。由图8可看出,迁移VGG参数的训练损失loss2收敛速度最快。但2种参数情况下的训练最终收敛在近似损失水平。
在迁移VGG参数的训练下,检测物体的平均精度均值的变化如图9所示。由图9可见,除30 000步的检测结果外,训练120 000步之前平均精度均逐渐提升。在120000步至终止训练阶段,平均精度均值出现振荡,分别于120 000步和140 000步达到高峰,因此最终检测的平均精度均值为80.5%。

图7 数据增广Fig.7 Data augmentation

图8 损失变化曲线Fig.8 Loss variation curves
3.1 基于异步卷积分解算法的shunt结构对实验结果的影响
FA-SSD中高层网络共使用了4个shunt结构,即shunt0、shunt1、shunt2和shunt3,如图5所示。为验证不同的shunt连接方式对网络检测结果的影响,实验通过调整shunt结构个数,分别搭建了shunt0000、shunt1000、shunt0101、shunt1110、shunt1111进行相同的训练与检测。其中,末尾数字串的前后数字顺序表示shunt0至shunt3结构的位置顺序。“0”表示去除FA-SSD中对应位置的shunt结构,“1”表示保留所在位置的shunt结构,例如Shunt0101表示图6中仅有shunt1与shunt3结构的FA-SSD网络结构。
不同数目shunt结构的检测精度如图10所示。由图10可见,仅加深高层主流网络深度后,shunt0000网络检测平均精度均值为77.8%,相对SSD提高0.6%,说明增加回归特征图之间的卷积层数可提高检测精度。此后,每增加一个shunt结构,网络在保证实时性的同时,进一步提高了平均检测精度。最后 shunt1111(FASSD300)网络的检测平均精度均值达到最高的80.5%,相对SSD提高了3.3%。由平均精度均值提高的幅度可推断,仅增加高层主流网络的卷积层数是提高平均精度均值的次要因素,交错连接的shunt结构是检测精度提高的主要原因。在增加了shunt结构后,FA-SSD300平均精度均值达到了最高的80.5%,同时保证了检测的实时性。
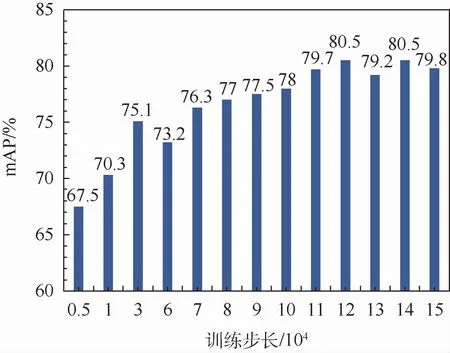
图9 不同迭代次数下的平均精度均值Fig.9 Mean average precision under different numbers of iteration
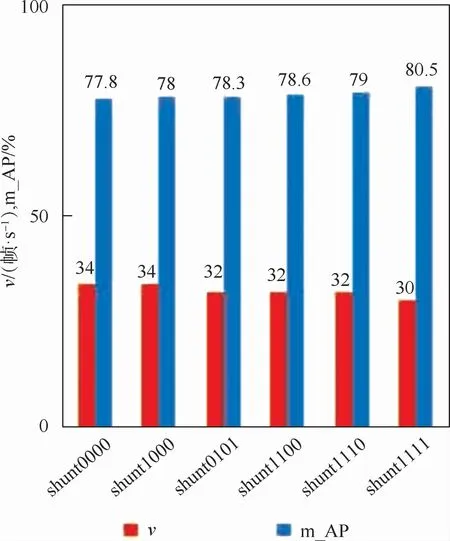
图10 不同数目的shunt结构对检测的影响Fig.10 Influence of different numbers of shunt structure on detection
3.2 高层网络优化对实验的影响
为优化异步卷积分解与shunt结构的融合,进一步提高特征的多样性,本文搭建了如图11所示的3种高层局部网络结构(shunt并联网络结构)。图11(a)表示SSD原有的kernal3×3s(2,2)卷积层与shunt结构的结合,图11(b)与(c)分别表示异步卷积分解结构、最大池化层和shunt结构的搭配。图11(a)、(b)和(c)分别对应的网络结构 为FA-SSD0、FA-SSD1、FA-SSD2。FA-SSD1与FA-SSD2中的主流结构中的不同部分,在图11中标记为红色。为保证FA-SSD1与FS-SSD2的主流结构深度相同(卷积层数与池化层数),结构(c)相比(b)增加一层kernal1×1s(1,1)的卷积层。在相同条件下对上述3种网络进行训练后,在VOC2007test上的检测结果如图12所示。FASSD0的平均精度均值为78.3%,相对SSD提升1.1%,检测速度虽然相对SSD降低11帧/s,但依然能保证实时检测。FASSD1采用异步卷积分解结构对主流特征图进行降维,平均精度均值达到80%,相比SSD提高2.8%。主流结构采用最大池化降维时,目标检测的精度与速度都有进一步的提升。FA-SSD2相比FA-SSD1在平均精度均值和检测速度上都提高0.5%。FA-SSD1与FASSD2在结构上的主要区别是主流结构上的降维计算方式。FA-SSD1采用一种异步卷积分解结构同时进行特征提取与降维,而FA-SSD2采用异步卷积分解和池化2种不同的降维计算方式,提高特征的多样性。由于池化计算相对异步卷积分解结构更简单,FA-SSD2相对FA-SSD1提高了检测速度。异步卷积分解相对池化更有利于传递空间相关信息,同时2种降维方式提高了特征的多样性,因此FA-SSD2检测精度达到最高的80.5%。

图11 高层网络的优化Fig.11 Optimization of high-level network

图12 高层结构优化对检测的影响Fig.12 Influence of high-level structure optimization on detection
3.3 对比实验
实验通过端到端的方法训练FA-SSD300,与近期算法在VOC2007和VOC2012(07+12)中训练,在VOC2007上进行了对比,结果如表1所示,Faster RCNN与R-FCN属于两阶段分类回归算法,虽然训练用到分辨率最大的图像,但平均精度均值仍然最低,且不具备实时检测能力。先后出现的单阶段回归系列算法 YOLOv2、SSD300、DSOD300以及DSSD321的检测平均精度均值逐步提升。其中,SSD类算法DSOD300、DSSD321虽然较前几种算法取得了更高的检测精度,但不能保证实时性,检测速度分别为17.4帧/s和9.5帧/s。FA-SSD300检测平均精度均值最高,达到80.5%,且保证了实时检测。为公平对比检测速度,采用与本实验相同的硬件,对SSD的检测速度进行测试,检测结果为表1中的SSD300*所示数据。
8种算法在VOC2007test上针对20个常见类别的具体检测结果对比如表2所示。其中,最高平均精度均值和每个类最高平均精度已标记为黑色粗体数字。
表2中左列5种算法为两阶段分类回归系列算法,右列3种算法为单价段回归算法,2类算法各自平均精度最高的网络分别是R-FCN与FASSD300。虽然与FA-SSD300同样达到80.5%的平均精度均值,但是R-FCN采用信息提取能力更强的复杂网络结构ResNet-101[18],处理速度仅为7帧/s。除平均检测精度达到最高外,FA-SSD在20类检测中共有11类达到最高平均精度,其中“Bus”与“Cat”2个类的平均检测精度均超过90%,分别为90.2%和91.7%。
FA-SSD300在VOC2007test上的部分结果如图13所示,对难以检测的密集小目标、遮挡目标和局部大目标均取得了较好的检测结果。图13(e)由于像素分辨率低造成一个小目标漏检,同时(b)和(g)由于目标遮挡过于严重造成次要目标漏检,其他所有位置定位框架均在合理范围内。

算法 训练数据 预训练 底层网络 图片大小 建议框数 显卡 速度/(帧·s-1)m_AP/%Fast R-CNN[8] 07+12 √ VGGNet 600×1000*300 K40 3.125 66.9 Faster R-CNN[9]07+12 √ VGGNet 600×1 000* 300 K40 5 73.2 R-FCN[22] 07+12 √ VGGNet 600×1000 300 K40 5.8 75.6 YOLOv2[12] 07+12 √ Darknet-19 352×352 Titan X 81 73.7 SSD300[13] 07+12 × VGGNet 300×300 8 732 Titan X 46 74.3 SSD300[13] 07+12 √ VGGNet 300×300 8 732 Titan X 46 77.2 SSD300*[13] 07+12 × VGGNet 300×300 8 732 1080Ti 43.5 74 DSOD300[16] 07+12 × DS/64-192-48-1 300×300 8 732 Titan X 17.4 77.7 DSSD321[14] 07+12 √ ResNet 321×321 17 080 Titan X 9.5 78.6 FA-SSD300 07+12 × VGGNet 300×300 8 732 1080Ti 30 79.0 FA-SSD300 07+12 √VGGNet 300×300 8 732 1080Ti 30 80.5

类别 Fast R-CNN[8] Faster R-CNN[9] ION[22] R-FCN[23] MR-CNN[24] SSD300[13] DSSD321[14]FA-SSD300 Aero 77.0 76.5 79.2 79.9 80.3 79.5 81.9 86.4 Bike 78.1 79 83.1 87.2 84.1 83.9 84.9 85.9 Bird 69.3 70.9 77.6 81.5 78.5 76 80.5 79.6 Boat 59.4 65.5 65.6 72 70.8 69.6 68.4 73.3 Bottle 38.3 52.1 54.9 69.8 68.5 50.4 53.9 53.6 Bus 81.6 83.1 85.4 86.8 88 87 85.6 90.2 Car 78.6 84.7 85.1 88.5 85.9 85.7 86.2 89.2 Cat 86.7 86.4 87 89.8 87.8 88.1 88.9 91.7 Chair 42.8 52 54.4 67 60.3 60.3 61.1 60.0 Cow 78.8 81.9 80.6 88.1 85.2 81.5 83.5 84.3 Table 68.9 65.7 73.8 74.5 73.7 77 78.7 80.9 Dog 84.7 84.8 85.3 89.8 87.2 86.1 86.7 89.1 Horse 82.0 84.6 82.2 90.6 86.5 87.5 88.7 87.4 Mbike 76.6 77.5 82.2 79.9 85 83.97 86.7 86.5 Person 69.9 76.7 74.4 81.2 76.4 79.4 79.7 83.3 Plant 31.8 38.8 47.1 53.7 48.5 52.3 51.7 54.2 Sheep 70.1 73.6 75.8 81.8 76.3 77.9 78 83.2 Sofa 74.8 73.9 72.7 81.5 75.5 79.4 80.9 82.3 Train 80.4 83 84.2 85.9 85 87.6 87.9 89.2 Tv 70.4 72.6 80.4 79.9 81 76.8 79.4 78.5 mAP/% 70.0 73.2 75.6 80.5 78.2 77.2 78.6 80.5

图13 FA-SSD300在VOC2007test上的部分检测结果Fig.13 Partial detection results of FA-SSD300 on VOC2007test
4 结 论
本文基于SSD提出一种基于异步卷积分解与shunt结构的单阶段目标检测器。采用基于异步卷积分解的shunt结构,在没有进行主流结构优化前,检测的平均精度均值便可达到80.0%,在不增加计算量的同时,提升了提取特征的非线性表达能力,shunt结构与主流结构的交融提高了回归特征图之间的协调性与统一性。构造了包含池化与异步卷积分解的局部结构,优化原有高层主流网络结构,异步卷积分解与池化两种降维方式的结合,既有利于空间相关信息的传递,也有利于提高特征的多样性。增加shunt结构并优化主流结构后,平均精度均值达到80.5%,相比SSD提高3.3%,比DSSD321提高了1.9%,同时在一块1080ti显卡上取得30帧/s的平均处理速度。
FA-SSD在保证实时性检测的同时,其平均精度在未采用MS COCO数据库扩充训练数据的情况下,便超过近期提出的SSD类算法。为适用于移动终端的相关应用,下一步研究工作将侧重于进一步降低网络规模优化网络结构。
